Aufgaben zum Aufstellen von Geradengleichungen

1
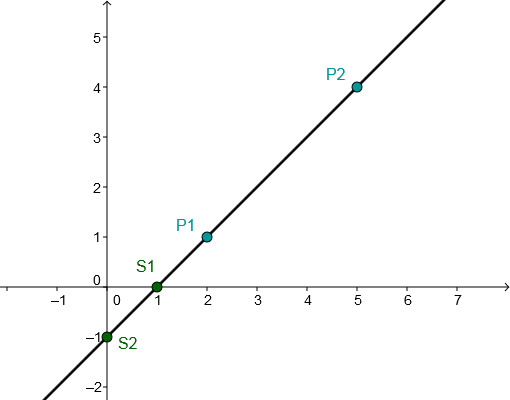
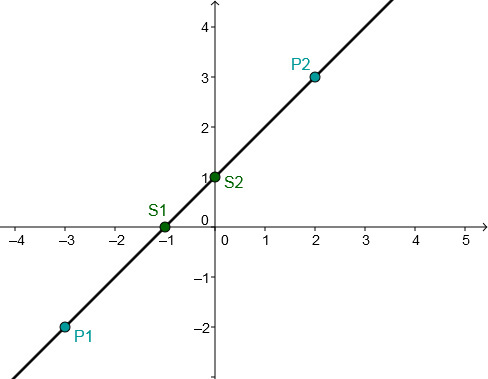
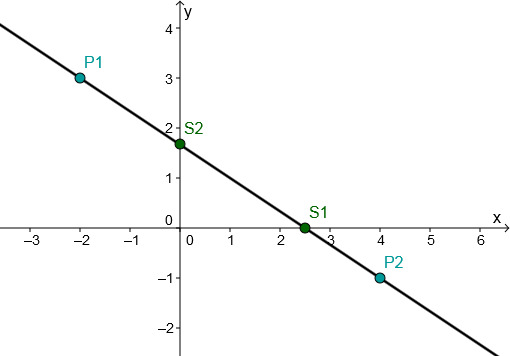
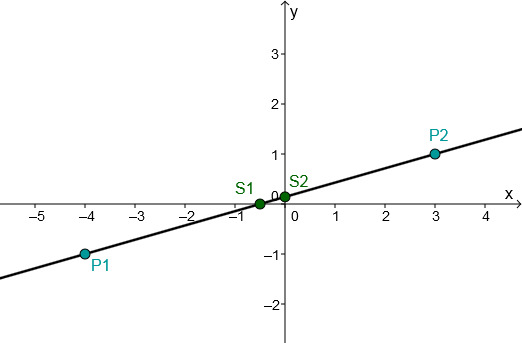
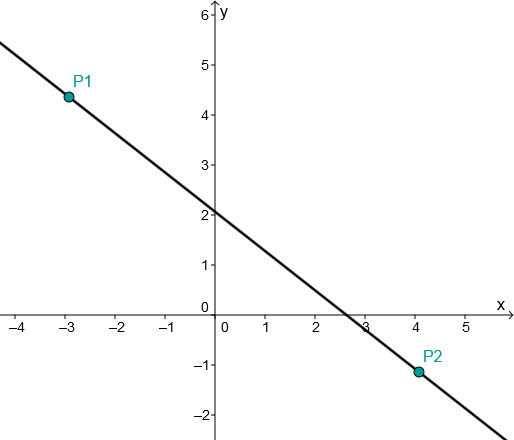
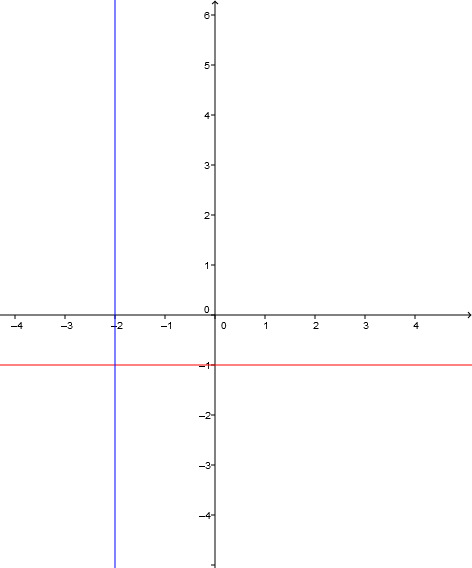
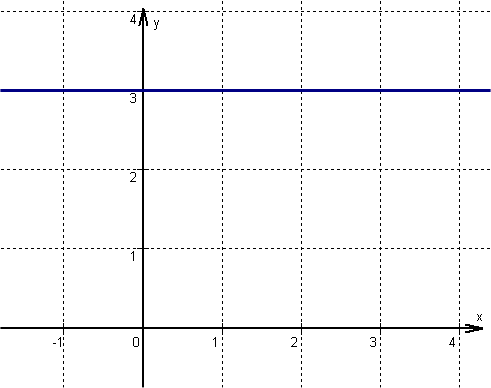
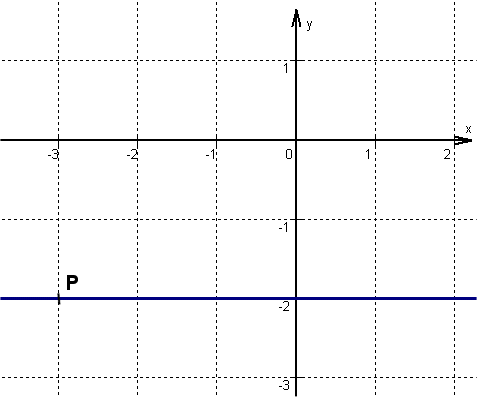
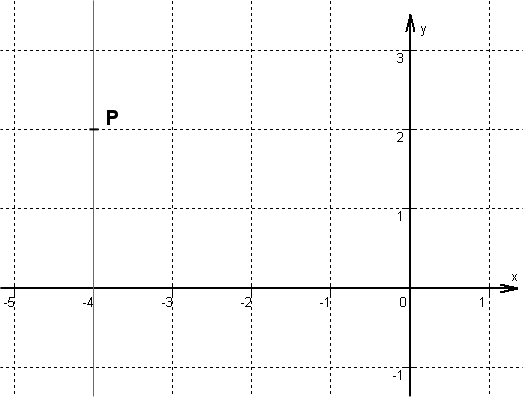
Bestimme die Gleichung der Geraden, die durch den Punkt P geht und senkrecht zur gegebenen Gerade steht.
$y = 3 x + 2$
$P (3 | 5)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu $g (x) : y = 3 x + 2$ senkrechten Geraden $h$ mit der Formel.
$m_{2} = - \frac{1}{m_{1}}$
Setz den Wert ein.
$m_{2} = - \frac{1}{3}$
Die gesuchte Senkrechte hat also Steigung $- \frac{1}{3}$ .
Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (3 | 5)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Setze die Werte ein.
$5 = - \frac{1}{3} \cdot 3 + b | + 1$
Vereinfache und addiere $1$ .
$6 = b \Leftrightarrow b = 6$
Also lautet die gesuchte Geradengleichung $h (x) : y = - \frac{1}{3} x + 6$ .

$y = 0,5 x + 1$
$P (1 | 2)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu $g (x) : y = 0,5 x + 1$ senkrechten Geraden $h$ mit der Formel.
$m_{2} = - \frac{1}{m_{1}}$
Setz den Wert ein.
$m_{2} = - \frac{1}{0,5} = - \frac{1}{\frac{1}{2}} = - 2$
Die gesuchte Senkrechte hat also Steigung $- 2$ .
Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (1 | 2)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Setz die Werte ein.
$2 = - 2 \cdot 1 + b$ $| + 2$
Vereinfache und addiere 2.
$4 = b \Rightarrow b = 4$
Also lautet die gesuchte Geradengleichung $h (x) : y = - 2 x + 4$ .

$y = - 5 x + 6$
$P (- 10 | 1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu $g (x) : y = - 5 x + 6$ senkrechten Geraden $h$ mit der Formel.
$m_{2} = - \frac{1}{m_{1}}$
Setz den Wert ein.
$m_{2} = - \frac{1}{- 5} = 0,2$
Die gesuchte Senkrechte hat also Steigung $0,2$ .
Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (- 10 | 1)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Setz die Werte ein.
$1 = 0,2 \cdot (- 10) + b$ $| + 2$
Vereinfache und addiere 2.
$3 = b \Rightarrow b = 3$
Also lautet die gesuchte Geradengleichung $h (x) : y = 0,2 x + 3$ .

$y = 4 x + 3$
$P (2 | - 5)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu $g (x) : y = 4 x + 3$ senkrechten Geraden $h$ mit der Formel.
$m_{2} = - \frac{1}{m_{1}}$
Setz den Wert ein.
$m_{2} = - \frac{1}{4} = - 0,25$
Die gesuchte Senkrechte hat also Steigung $- 0,25$ .
Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (2 | - 5)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Setz die Werte ein.
$- 5 = - 0,25 \cdot 2 + b$ $+ 0,5$
Vereinfache und addiere 0,5.
$- 4,5 = b \Rightarrow b = - 4,5$
Also lautet die Geradengleichung $h (x) : y = - 0,25 x - 4,5$ .

$y = - \frac{2}{3} x + 2$
$P (4 | 6)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu $g (x) : y = - \frac{2}{3} x + 3$ senkrechten Geraden $h$ mit der Formel.
$m_{2} = - \frac{1}{m_{1}}$
Setz den Wert ein.
$m_{2} = - \frac{1}{- \frac{2}{3}} = \frac{3}{2}$
Die gesuchte Senkrechte hat also Steigung $\frac{3}{2}$ .
Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (4 | 6)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Setz die Werte ein.
$6 = \frac{3}{2} \cdot 4 + b$ $| - 6$
Vereinfache und subtrahiere 6.
$0 = b \Rightarrow b = 0$
Also lautet die Geradengleichung $h (x) : y = \frac{3}{2} x$ .

$y = \frac{1}{3} x - 2$
$P (2 | 5)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung und Geradensteigung
Bestimme zunächst die Steigung der zu $g (x) : y = \frac{1}{3} x - 2$ senkrechten Geraden $h$ mit der Formel.
$m_{2} = - \frac{1}{m_{1}}$
Setz den Wert ein.
$m_{2} = - \frac{1}{\frac{1}{3}} = - 3$
Die gesuchte Senkrechte hat also Steigung $- 3$ .
Bestimme nun den y-Achsenabschnitt der Senkrechten $h$ mit dem gegebenen Punkt $P (2 | 5)$ , indem du den Punkt in die allgemeine Geradengleichung einsetzt.
$h (x_{p}) : y_{p} = m_{2} x_{p} + b$
Setz die Werte ein.
$5 = - 3 \cdot 2 + b$ $| + 6$
Vereinfache und addiere 6.
$11 = b \Rightarrow b = 11$
Also lautet die Geradengleichung $h (x) : y = - 3 x + 11$ .
2
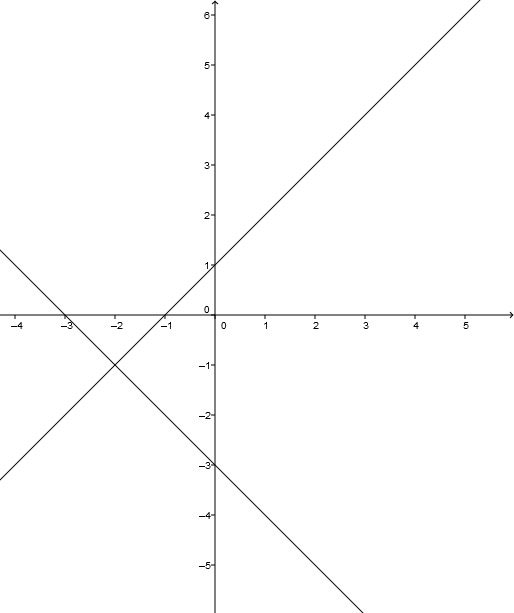
Bestimme die Gleichung der Geraden g, die parallel zur Geraden h ist und durch den Punkt P geht.
h: $y = 3 x - 2$ ; P(1|0)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
$y = 3 x - 2$ ; P(1|0)
Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
$m = 3$
Geradengleichung aufstellen
Setze m (3) und P(1|0) in die allgemeinen Geradengleichung ein.
$0$ $=$ $3 \cdot 1 + t$ $- 3$
↓
Gleichung nach t auflösen.
$t$ $=$ $- 3$
Setze m und t in die allgemeinen Geradengleichung ein.
$\Rightarrow$ Geradengleichung: $y = 3 x - 3$

h: $y = x - 4$ ; P(1|2)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
$y = x - 4$ ; P(1|2)
Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
$m = 1$
Gleichung aufstellen
Setze m (1) und P(1|2) in die allgemeinen Geradengleichung ein.
$2$ $=$ $1 + t$ $ - 1$
↓
Gleichung nach t auflösen.
$ t$ $=$ $1$
Setze m und t in die allgemeinen Geradengleichung ein.
$\Rightarrow$ Geradengleichung: $y = x + 1$

h: $y = 4 x$ ; P(5|18)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
$y = 4 x$ ; P(5|18)
Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
$m = 4$
Gleichung aufstellen
Setze m (4) und P(5|18) in die allgemeinen Geradengleichung ein.
$18$ $=$ $4 \cdot 5 + t$ $- 20$
↓
Gleichung nach t auflösen.
$t$ $=$ $- 2$
Setze m und t in die allgemeinen Geradengleichung ein.
$\Rightarrow$ Geradengleichung: $y = 4 x - 2$

h: $y = - 2 x + 1$ ; P(-1|4)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung bestimmen
$y = - 2 x + 1$ ; P(-1|4)
Damit die gesuchte Gerade parallel zu h ist, muss sie die selbe Steigung besitzen.
Die Steigung einer Gerade ist m der allgemeinen Geradengleichung.
$m = - 2$
Gleichung aufstellen
Setze m (-2) und P(-1|4) in die allgemeinen Geradengleichung ein.
$4$ $=$ $- 2 \cdot (- 1) + t$ $- 2$
↓
Gleichung nach t auflösen.
$t$ $=$ $2$
Setze m und t in die allgemeinen Geradengleichung ein.
$\Rightarrow$ Geradengleichung: $y = - 2 x + 2$
3
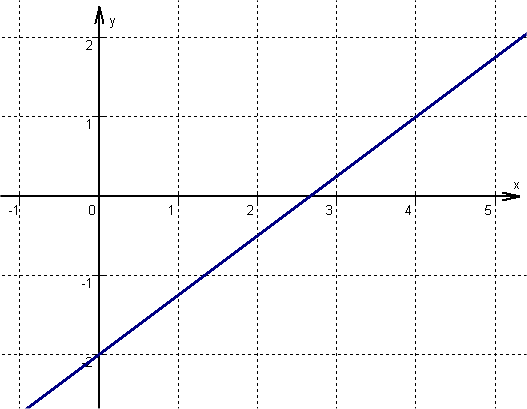
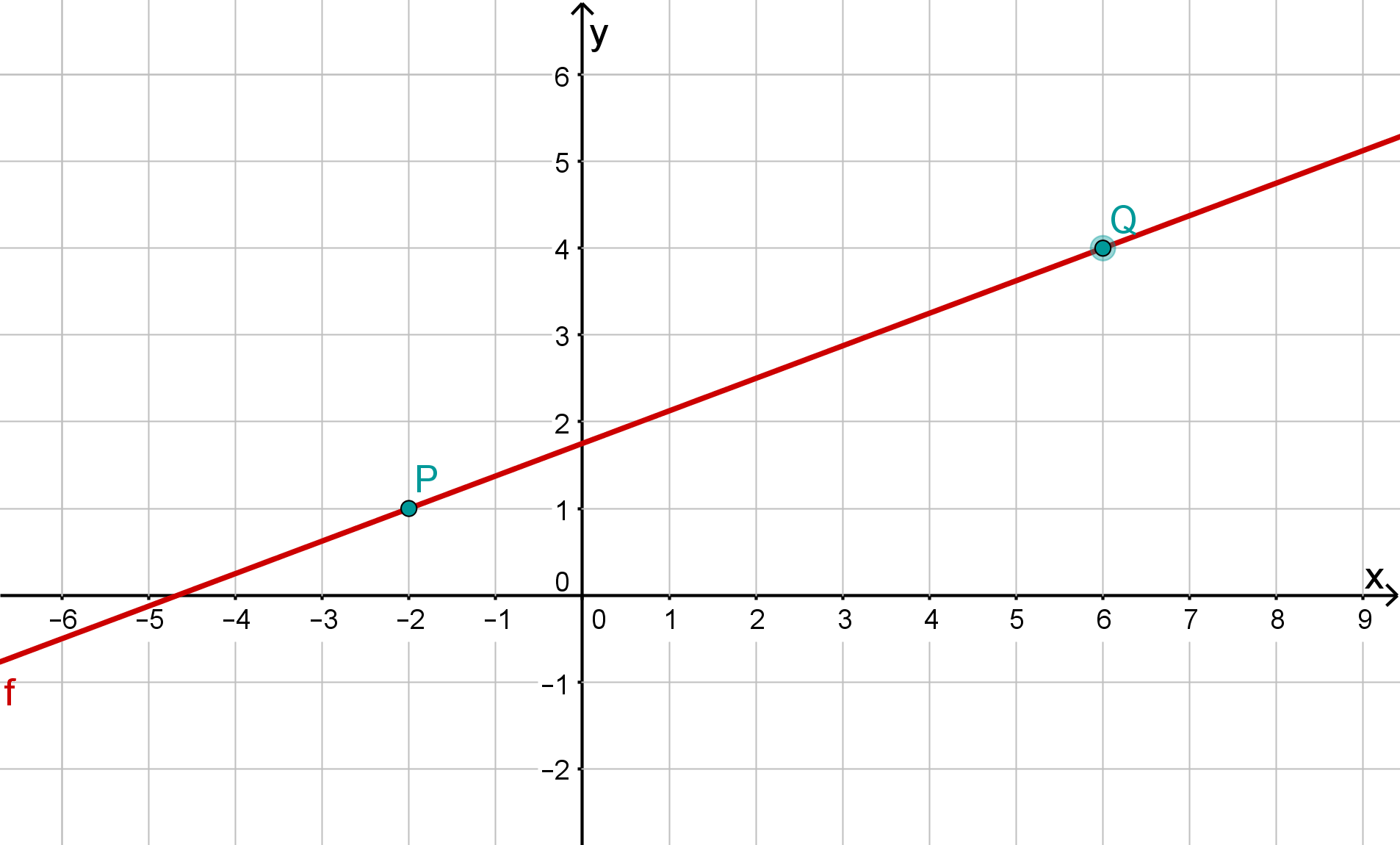
Berechne die Steigung der Gerade durch die gegebenen Punkte.
$A (5 | 7)$ , $B (- 3 | 8)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung
$A (5 | 7), B (- 3 | 8)$
Setze die Punkte in den Differenzenquotient für die Gerade ein.
$m$ $=$ $\frac{8 - 7}{- 3 - 5}$
↓
Vereinfache Zähler und Nenner
$m$ $=$ $\frac{1}{- 8}$
$m$ $=$ $- \frac{1}{8}$
Die Steigung der Geraden beträgt $m = - \frac{1}{8}$ .

$A (1 | 2)$ , $B (3 | 4)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung
$A (1 | 2), B (3 | 4)$
Setze die Punkte in den Differenzenquotient für die Gerade ein.
$m$ $=$ $\frac{4 - 2}{3 - 1}$
↓
Vereinfache Zähler und Nenner
$m$ $=$ $\frac{2}{2}$
$m$ $=$ $1$
Die Steigung der Geraden beträgt m = 1.

Funktionsgleichung bestimmen.

Eine Gerade hat die Steigung $a_{1}$ und verläuft durch den Punkt P. Bestimmen Sie die Funktionsgleichung f(x), die Achsenschnittpunkte und zeichnen Sie den Graphen.

$a_{1} = \frac{1}{2}$ $P (4 | - 2)$

$a_{1} = \frac{3}{4} P (1 | - 3)$

$a_{1} = 2 P (3 | - 1)$

$a_{1} = \frac{4}{5} P (\frac{3}{2} | 4)$

5
Löse die folgenden Aufgaben.
Welche Steigung hat die Gerade durch die Punkte $P (0 | 3)$ und $Q (2 | - 3)$ ?

Für diese Aufgabe benötigst Du folgendes Grundwissen: allgemeine Geradengleichung
Gegeben: Punkt $P (0 | 3)$ und Punkt $Q (2 | - 3)$
Setze die x-Werte (erste Koordinate) und die y-Werte (zweite Koordinate) in die allgemeine Geradengleichung ein.
$3 = m \cdot 0 + t$
$- 3 = m \cdot 2 + t$
Bei der ersten Gleichung kannst du sofort ablesen, dass $t = 3$ . Dieses $t$ kannst du in die zweite Gleichung einsetzen, um $m$ auszurechnen.
$- 3$ $=$ $m \cdot 2 + 3$ $- 3$
$- 6$ $=$ $m \cdot 2$ $: 2$
$- 3$ $=$ $m$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
$y = - 3 x + 3$

Stelle die Gleichung der Geraden durch die Punkte $P (1 | 3)$ und $Q (3 | - 1)$ auf.

Gegeben: Punkt $P (1 | 3)$ und $Q (3 | - 1)$
Berechne die Differenz der beiden x-Werte und der beiden y-Werte, um die Steigung zu bestimmen.
x-Werte: $3 - 1 = 2$
y-Werte: $- 1 - 3 = - 4$
Während der x-Wert um $2$ steigt, nimmt der y-Wert um $4$ ab. Dividiere den y-Wert durch den x-Wert, um die Steigung auszurechnen.
$m = \frac{- 4}{2} = - 2$
Setze m, den x-Wert und den y-Wert eines der Punkte in die allgemeine Geradengleichung ein, um $t$ zu bestimmen.
$3$ $=$ $- 2 \cdot 1 + t$
$3$ $=$ $- 2 + t$ $+ 2$
$t$ $=$ $5$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein, um die Gleichung der Funktion aufzustellen.
$y = - 2 x + 5$

Funktionsgleichung bestimmen.

Eine Gerade verläuft durch die Punkte $P_{1}$ und $P_{2}$ . Bestimmen Sie die Funktionsgleichung f(x), die Achsenschnittpunkte und zeichnen Sie den Graphen.

$P_{1} (2 | 1) P_{2} (5 | 4)$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung der Funktionsgleichung
Setze $P_{1}$ und $P_{2}$ in die allgemeine Geradengleichung ein.
$y = m \cdot x + t$
Wende das Additionsverfahren an.
$\begin{array}{l} 1) 1 = m \cdot 2 + t \\ 2) 4 = m \cdot 5 + t \end{array}$
$1) - 2) - 3$ $=$ $- 3 m$ $: (- 3)$
$m$ $=$ $1$
Setze m in 1) ein.
$1$ $=$ $1 \cdot 2 + t$ $- 2$
$t$ $=$ $- 1$
Setze t und m in die allgemeine Geradengleichung ein.
$y = x - 1 \Rightarrow f (x) = x - 1$
Bestimmung der Achsenschnittpunkte
Setze y=0, um den Schnittpunkt mit der x-Achse zu bestimmen
$x - 1$ $=$ $0$ $+ 1$
$x_{N}$ $=$ $1$
Der Schnittpunkt mit der x-Achse ist $S_{1} (1 | 0)$
Der Schnittpunkt mit der y-Achse entspricht dem y-Achsenabschnitt (t) $\Rightarrow S_{2} (0 | - 1)$
Zeichnung
Verbinde entweder die beiden Achsenschnittpunkte $S_{1}$ und $S_{2}$ oder die beiden vorgegebenen Punkte $P_{1}$ und $P_{2}$ .
Oder Wähle einen dieser Punkte und gehe entsprechend der Steigung eins nach rechts und eins nach oben und verbinde diese beiden Punkte.
$P_{1} (- 3 | - 2) P_{2} (2 | 3)$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung der Funktionsgleichung
Setze $P_{1}$ und $P_{2}$ in die allgemeine Geradengleichung ein.
$\begin{array}{l} y = m \cdot x + t \end{array}$
Wende das Additionsverfahren an.
$\begin{array}{l} \begin{array}{l} 1) - 2 = m \cdot (- 3) + t \\ 2) 3 = m \cdot 2 + t \end{array} \end{array}$
$1) - 2) - 5$ $=$ $- 5 m$ $: (- 5)$
$m$ $=$ $1$
↓
Setze m in 2) ein.
$3$ $=$ $2 + t$ $- 2$
$t$ $=$ $1$
↓
Setze m und t in die allgemeine Geradengleichung ein.
$y$ $=$ $x + 1 \Rightarrow f (x) = x + 1$
Bestimmung der Achsenschnittpunkte
Setze y=0, um den Schnittpunkt mit der x-Achse zu bestimmen
$x + 1$ $=$ $0$ $- 1$
$x_{N}$ $=$ $- 1$
Der Schnittpunkt mit der x-Achse ist $S_{1} (- 1 | 0)$ .
Der Schnittpunkt mit der y-Achse entspricht dem y-Achsenabschnitt $\Rightarrow S (0 | 1)$
Zeichnung
Verbinde entweder die beiden Achsenschnittpunkte $S_{1}$ und $S_{2}$
oder die beiden vorgegebenen Punkte $P_{1}$ und $P_{2}$ .
Oder Wähle einen dieser Punkte und gehe entsprechend der Steigung eins nach rechts und eins nach oben und verbinde diese beiden Punkte.

$P_{1} (- 2 | 3) P_{2} (4 | - 1)$

$P_{1} (- 4 | - 1) P_{2} (3 | 1)$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung der Funktionsgleichung
$\begin{array}{l} y = mx + t \end{array}$
Setze $P_{1}$ und $P_{2}$ in die allgemeine Geradengleichung ein.
$\begin{array}{l} \begin{array}{l} 1) - 1 = - 4 m + t \\ 2) 1 = 3 m + t \end{array} \end{array}$
Wende das Additionsverfahren an. Berechne $1) - 2)$
$- 2$ $=$ $- 7 m$ $: (- 7)$
$m$ $=$ $\frac{2}{7}$
↓
Setze $m$ in $2)$ ein.
$1$ $=$ $\frac{2}{7} \cdot 3 + t$ $- \frac{6}{7}$
$t$ $=$ $1 - \frac{6}{7}$
$t$ $=$ $\frac{1}{7}$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
$y = \frac{2}{7} x + \frac{1}{7} \Rightarrow f (x) = \frac{2}{7} x + \frac{1}{7}$
Bestimmung der Achsenschnittpunkte
Setze $y = 0$ , um den Schnittpunkt mit der $x$ -Achse zu bestimmen
$\frac{2}{7} x + \frac{1}{7}$ $=$ $0$ $- \frac{1}{7}$
$\frac{2}{7} x$ $=$ $- \frac{1}{7}$ $: \frac{2}{7}$
$x$ $=$ $\frac{- \frac{1}{7}}{\frac{2}{7}}$
↓
Dividiere die Brüche. $\to$ Multipliziere mit dem Kehrwert.
$x$ $=$ $- \frac{1}{7} \cdot \frac{7}{2}$
$x_{N}$ $=$ $- \frac{1}{2}$
Der Schnittpunkt mit der x-Achse ist $S_{1} (- \frac{1}{2} | 0)$ .
Schnittpunkt mit der y-Achse entspricht dem y-Achsenabschnitt $\Rightarrow S_{2} (0 | \frac{1}{7})$
Zeichnung
Verbinde entweder die beiden Achsenschnittpunkte $S_{1}$ und $S_{2}$ ,
oder die beiden vorgegebenen Punkte $P_{1}$ und $P_{2}$ .
Oder Wähle einen dieser Punkte und gehe entsprechend der Steigung sieben nach rechts und zwei nach oben und verbinde diese beiden Punkte.
$P_{1} (- 3 | \frac{9}{2}) P_{2} (4 | - 1)$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung der Funktionsgleichung
$\begin{array}{l} y = mx + t \end{array}$
Setze $P_{1}$ und $P_{2}$ in die allgemeine Geradengleichung ein.
$\begin{array}{l} \begin{array}{l} 1) \frac{9}{2} = - 3 m + t \\ 2) - 1 = 4 m + t \end{array} \end{array}$
Wende das Additionsverfahren an. Berechne $1) - 2) :$
$\frac{11}{2}$ $=$ $- 7 m$ $: (- 7)$
$m$ $=$ $\frac{\frac{11}{2}}{- 7}$
$m$ $=$ $- \frac{11}{14}$
Setze $m$ in $2)$ ein.
$- 1$ $=$ $- \frac{11}{14} \cdot 4 + t$
$- 1$ $=$ $- \frac{44}{14} + t$ $+ \frac{44}{14}$
$\begin{array}{l} t = \frac{30}{14} \end{array}$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
$y = - \frac{11}{14} x + \frac{30}{14}$
Bestimmung der Achsenschnittpunkte
Setze y=0, um den Schnittpunkt mit der $x$ -Achse zu bestimmen.
$- \frac{11}{14} x + \frac{30}{14}$ $=$ $0$ $- \frac{30}{14}$
$- \frac{11}{14} x$ $=$ $- \frac{30}{14}$ $: (- \frac{11}{14})$
↓
Dividiere die Brüche. Das heißt multipliziere mit dem Kehrbruch.
$x$ $=$ $- \frac{30}{14} \cdot (- \frac{14}{11})$
$x_{N}$ $=$ $\frac{30}{11}$
Der Schnittpunkt mit der x-Achse ist $S_{1} (\frac{30}{11} | 0)$
Der Schnittpunkt mit der y-Achse entspricht dem y-Achsenabschnitt $\Rightarrow S (0 | \frac{30}{14})$
Zeichnung
Verbinde die beiden vorgegebenen Punkte $P_{1}$ und $P_{2}$ .
Oder Wähle einen dieser Punkte und gehe entsprechend der Steigung 14 nach rechts und 11 nach unten und verbinde diese beiden Punkte.
$P_{1} (- 4 | - 2) P_{2} (\frac{7}{2} | 4)$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung der Funktionsgleichung
$\begin{array}{l} y = mx + t \end{array}$
Setze $P_{1}$ und $P_{2}$ in die allgemeine Geradengleichung ein.
$\begin{array}{l} \begin{array}{l} 1) - 2 = - 4 m + t \\ 2) 4 = 3,5 m + t \end{array} \end{array}$
Wende das Additionsverfahren an. Berechne $1) - 2)$ :
$- 6$ $=$ $- 7,5 m$ $: (- 7,5)$
$m$ $=$ $\frac{- 6}{- 7,5}$
$m$ $=$ $0,8$
↓
Setze $m$ in $1)$ ein.
$- 2$ $=$ $0,8 \cdot (- 4) + t$
$- 2$ $=$ $- 3,2 + t$ $+ 3,2$
$\begin{array}{l} t = 1,2 \end{array}$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
$y = 0,8 x + 1,2 \Rightarrow f (x) = 0,8 x + 1,2$
Bestimmung der Achsenschnittpunkte
Setze $y = 0$ , um den Schnittpunkt mit der $x$ -Achse zu bestimmen
$0,8 x + 1,2$ $=$ $0$ $- 1,2$
$0,8 x$ $=$ $- 1,2$ $: 0,8$
$x$ $=$ $\frac{- 1,2}{0,8}$
$x_{N} = - 1,5$
Der Schnittpunkt mit der x-Achse ist $S_{1} (- 1,5 | 0)$
Der Schnittpunkt mit der y-Achse entspricht dem y-Achsenabschnitt $\Rightarrow S (0 | 1,2)$
Zeichnung
Verbinde entweder die beiden Achsenschnittpunkte $S_{1}$ und $S_{2}$ ,
oder die beiden vorgegebenen Punkte $P_{1}$ und $P_{2}$ .
Oder Wähle einen dieser Punkte und gehe entsprechend der Steigung 1 nach rechts und 0,8 nach oben und verbinde diese beiden Punkte.

7
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Zwei aufeinander senkrecht stehende Geraden schneiden sich in $S (- 2 | - 1)$ .
Geben Sie mögliche Geradengleichungen an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Wir haben zwei zueinander senkrechte Geraden mit dem Schnittpunkt $(- 2, - 1)$ . Wie man aus der Angabe schon rauslesen kann, gibt es mehrere Möglichkeiten, zwei solcher Geraden zu wählen. Im Folgenden wird eine Möglichkeit angegeben. Ein gutes Kriterium, um zu überprüfen, ob die zwei gewählten Geraden senkrecht zueinander sind, ist folgendes:
$m_{1} \cdot m_{2} = - 1$ .
Wähle zum Beispiel die Geraden g mit $y = g (x) = x + 1$ und h mit $y = h (x) = - x - 3$ . Dann gilt $m_{1} \cdot m_{2} = 1 \cdot (- 1) = - 1$ und es gilt $g (- 2) = - 1$ und $h (- 2) = - 1$ . Also liegt der Schnittpunkt auf den beiden Geraden und diese sind senkrecht zueinander.
Achtung:
Wählst du zum Beispiel die Gerade $y = - 1$ (eine Parallele zur x-Achse), die durch den Punkt $(- 2, - 1)$ geht, gibt es genau eine Gerade, nämlich die Gerade, die parallel zur y-Achse steht mit der Geradengleichung $x = - 2$ . Diese stehen zwar senkrecht aufeinander, aber $x = - 2$ ist keine Funktion, sondern eine Relation.
8
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Welche Steigung hat die Gerade durch die Punkte $P (0 | 3)$ und $Q (2 | - 3)$ ? Wie lautet also die Funktionsgleichung?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Steigung
Bestimme die Steigung $m$ .
$m = \frac{△ y}{△ x} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$
Setze die beiden Punkte in die Formel für die Steigung ein.
$m = \frac{3 - (- 3)}{0 - 2} = \frac{6}{- 2} = - 3$
Funktionsgleichung
Bestimme die Funktionsgleichung.
$y = m \cdot x + t$
Setze m in die allgemeine Geradengleichung ein.
$y = - 3 x + t$
Setze einen der beiden Punkte in die Funktionsgleichung ein.
$3 = - 3 \cdot 0 + t$
$t = 3$
Setze t in die Funktionsgleichung ein.
$\Rightarrow f (x) = - 3 x + 3$
9
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Stelle die Gleichung der Geraden durch die Punkte $P (1 | 3)$ und $Q (3 | - 1)$ auf.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Gegeben sind die beiden Punkte $P (1 | 3)$ und $Q (3 | - 1)$ .
Gesucht ist die Gleichung der Geraden, die durch die beiden Punkte geht.
Zur Ermittlung der Geradengleichung überlegst du am Besten erst die allgemeine Form der Geradengleichung:
Bestimmung der Steigung $m$
Erinnere dich zunächst an die Gleichung für die Steigung einer Geraden:
$m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$
Setze die Werte $x_{1}, x_{2}, y_{1}, y_{2}$ aus den Punkten $P$ und $Q$ in die Formel ein.
$m = \frac{- 1 - 3}{3 - 1} = \frac{- 4}{2}$
Kürze den Bruch.
$m = - 2$
Jetzt weißt du, dass die Gleichung der Geraden durch die Punkte $P$ und $Q$ geht folgendermaßen aussieht:
$y = - 2 \cdot x + t .$
Als nächstes ermittelst du den $y$ -Achsenabschnitt ( $t$ ).
Ermittlung des $y$ -Achsenabschnitts $t$
Um $t$ zu ermitteln setzt du den $x$ - und $y$ -Wert einer der beiden Punkte in die Geradengleichung ein. Hier wird das beispielhaft mit dem Punkt $P$ ausgerechnet.
$3 = - 2 \cdot 1 + t$
$3 = - 2 + t$
$t = 5$
Der $y$ -Achsenabschnitt der Funktion ist $5$ . Damit hast du auch schon die ganze Funktionsgleichung.
$y = - 2 \cdot x + 5$
10
Zeichne die folgenden Geraden und gib den Funktionsterm an.
$G_{f}$ hat die Steigung $\frac{3}{4}$ und schneidet die y-Achse bei $- 2$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Aufstellen einer Geradengleichung
Funktionsterm aufstellen
$m = \frac{3}{4}; t = - 2$
Setze $m$ und $t$ in die allgemeine Geradengleichung $y = m x + t$ ein.
$\Rightarrow y = \frac{3}{4} x - 2$
Gerade zeichnen
Wähle einen beliebigen Punkt auf der Geraden, z. B. den Schnittpunkt mit der $y$ -Achse $(0 | - 2)$ . Gehe von dort $1$ nach rechts und entsprechend der Steigung $m = \frac{3}{4}$ nach oben (Alternativ auch die vierfache Länge, um Brüche zu vermeiden: $4$ nach rechts und $3$ nach oben). Verbinde die beiden Punkte zu einer Geraden.

$G_{f}$ hat die Steigung $0$ und schneidet die y-Achse bei $3$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Aufstellen einer Geradengleichung
Funktionsterm aufstellen
$m = 0; t = 3$
Setze $m$ und $t$ in die allgemeine Geradengleichung $y = m x + t$ ein.
$\Rightarrow y = 3$
Gerade zeichnen
Die Gerade verläuft durch den Schnittpunkt mit der $y$ -Achse $(0 | 3)$ parallel zur $x$ -Achse, da die Gerade die Steigung $0$ hat.

$G_{f}$ geht durch den Punkt $P (- 3 | - 2)$ und ist parallel zur $x$ -Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Aufstellen einer Geradengleichung
Funktionsterm aufstellen
Da die Gerade parallel zur $x$ -Achse liegt, ist ihre Steigung $0$ $\Rightarrow m = 0$ .
Die Gerade geht durch den Punkt $(- 3 | - 2)$ . Da die Steigung $0$ ist, hat die Gerade bei $x = 0$ den y-Wert $- 2$ .
Ihr $y$ -Achsenabschnitt liegt also bei $- 2 \Rightarrow t = - 2.$
$m = 0; t = - 2$
Setze $m$ und $t$ in die allgemeine Funktion $y = m x + t$ ein.
$y = - 2$
Gerade zeichnen
Die Gerade verläuft durch den Schnittpunkt mit der $y$ -Achse $(0 | - 2)$ parallel zur $x$ -Achse, da die Gerade die Steigung $0$ hat.

$G_{f}$ geht durch den Punkt $P (- 4 | 2)$ und ist parallel zur $y$ -Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Aufstellen einer Geradengleichung
Funktionsterm aufstellen
Diese Gerade kann nicht durch eine Funktionsgleichung beschrieben werden. Die Steigung wäre unendlich groß.

Wir können die Gerade aber trotzdem zeichnen.
Gerade zeichnen
Die Gerade verläuft durch den Punkt $(- 4 | 2)$ parallel zur $y$ -Achse.
11
Stelle die Funktionsgleichung für die Gerade durch die Punkte P(-25|30) und Q(55|-30) auf und berechne den Schnittpunkt der Gerade mit der x-Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung ermitteln
P(-25|30); Q(55|-30)
Ermittle die Steigung m der allgemeinen Geradengleichung mithilfe des Differenzenqotienten .
$m = \frac{30 - (- 30)}{- 25 - 55} = \frac{60}{- 80} = - \frac{3}{4}$
Setze m und die Koordinaten eines Punktes z. B. P(-25|30) in die allgemeine Geradengleichung ein.
$30 = \frac{- 3}{4} (- 25) + t$
Vereinfache: $\frac{- 3}{4} (- 25) = \frac{- 3 (- 25)}{4} = \frac{3 \cdot 25}{4} = \frac{75}{4}$
$30$ $=$ $\frac{75}{4} + t$ $- \frac{75}{4}$
↓
Löse nach t auf.
$t$ $=$ $30 - \frac{75}{4}$
$t$ $=$ $\frac{45}{4}$
↓
Setze m und t in die allgemeine Geradengleichung ein.
$\Rightarrow y = - \frac{3}{4} x + \frac{45}{4}$
Schnittpunkt mit der x-Achse
An der Schnittstelle mit der x-Achse ist der y-Wert 0.
$0 = \frac{- 3}{4} x + \frac{45}{4}$
Nach x auflösen. Stelle dafür das x alleine durch: $| \cdot \frac{- 4}{3}$
Beachte, dass bei beide Summanden multipliziert werden müssen.
$0 = \frac{(- 3) (- 4)}{4 \cdot 3} x + \frac{45 (- 4)}{4 \cdot 3}$
$\frac{(- 3) (- 4)}{4 \cdot 3} = \frac{3 \cdot 4}{12} = \frac{12}{12} = 1$
$0 = x + \frac{- 180}{12}$
$0 = x - 15$
Addiere 15
$x = 15$
$\Rightarrow$ Die Gerade schneidet die x-Achse bei S(15|0).

Stelle die Gleichung der Geraden mit Steigung $m = - \frac{4}{3}$ durch den Punkt $P (- 2 | - 0,5)$ auf und zeichne sie in ein Koordinatensystem.

13
Bestimme die Gleichung der Geraden, die durch …
den Punkt $P (- 3 | 4)$ geht und parallel ist zur $x$ -Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Parallel zur $x$ -Achse, das heißt die gleiche Steigung wie die $x$ -Achse, also $m = 0$ .
$m$ und $P$ in die allgemeine Geradengeleichung einsetzen.
$\begin{array}{rcl} 4 & = & 0 \cdot (- 3) + t \\ 4 & = & t \end{array}$
Zur Geradengleichung zusammensetzen.
$y = 0 \cdot x + 4 = 4$

den Punkt $Q (2 | 5)$ geht und parallel ist zur Winkelhalbierenden des 2.Quadranten.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Parallel zur Winkelhalbierenden des 2. Quadranten bedeutet gleiche Steigung.
Die Steigung der Winkelhalbierenden des 2. Quadranten ist -1
$\Rightarrow m = - 1$
$m$ in die Geradengleichung einsetzen und damit $t$ berechnen.
$\begin{array}{rcl} 5 & = & - 2 + t & | + 2 \\ t & = & 7 \end{array}$
$m$ und $t$ in die allgemeine Geradengleichung einsetzen.
$y = - 1 \cdot x + 7 = - x + 7$

den Punkt $R (- 4 | 2)$ geht und parallel ist zur $y$ -Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Parallel zur $y$ -Achse, d.h. keine Funktionsgleichung, da einem $x$ -Wert unendlich viele $y$ -Werte zugeordnet werden. Die Gerade kann also nur als der $x$ -Wert von $R$ beschrieben werden.
$\Rightarrow x = - 4$

den Punkt $S (2 | - 3)$ geht und parallel ist zur Winkelhalbierenden des 1.Quadranten.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Parallel zur Winkelhalbierenden des 1. Quadranten bedeutet die gleiche Steigung.
Die Steigung der Winkelhalbierenden des 1. Quadranten ist 1.
$\Rightarrow m = 1$
Setze m und S in die allgemeine Geradengleichung ein und löse nach $t$ auf.
$\begin{array}{rcl} - 3 & = & 2 + t & | - 2 \\ t & = & - 5 \end{array}$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
$\Rightarrow y = x - 5$

den Ursprung geht und parallel ist zur Geraden $AB$ mit $A (- 72 | - 60)$ und $B (- 24 | - 20)$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Durch den Ursprung, das heißt $y$ -Achsenabschnitt $t = 0$
Parallel zur Geraden $AB$ , bedeutet die gesuchte Gerade hat die gleiche Steigung wie $AB$ .
$A (- 72 | - 60); B (- 24 | - 20)$
Berechne die Steigung $m$ mithilfe des Differenzenquotienten .
$m = \frac{- 20 - (- 60)}{- 24 - (- 72)} = \frac{40}{48} = \frac{5}{6}$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
$\Rightarrow y = \frac{5}{6} x$
14
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Prüfen Sie, ob die Gerade durch $P_{1}$ und $P_{2}$ eine Ursprungsgerade ist.
$P_{1} (2 | 4); P_{2} (- 1,5 | - 3)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Setze die beiden Punkte in die allgemeine Geradengleichung ein:
$y = mx + t$
$\begin{aligned} 1) & 4 & = & 2 m + t \\ 2) & - 3 & = & - 1,5 m + t & | \cdot (- 1) \end{aligned}$
$\begin{aligned} 1) & 4 & = & 2 m + t \\ 2) & 3 & = & 1,5 m - t \end{aligned}$
Wende das Additionsverfahren an.
Berechne $1) + 2)$ .
$7$ $=$ $3,5 m$ $: 3,5$
$m$ $=$ $\frac{7}{3,5}$
$m$ $=$ $2$
Setze m in eine der beiden Funktionen ein.
$4$ $=$ $2 \cdot 2 + t$
$4$ $=$ $4 + t$ $- 4$
$t$ $=$ $4 - 4$
$t$ $=$ $0$
$y = 2 x$
Die Gerade durch $P_{1}$ und $P_{2}$ ist eine Ursprungsgerade, da für $x = 0$ der y-Wert gleich $0$ ist.

$P_{1} (- 1 | 3,5); P_{2} (2 | - 2)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktionen
Setze die beiden Punkte in die allgemeine Geradengleichung ein:
$y = m x + t$
$\begin{array}{l} 1) 3,5 = - 1 m + t \\ 2) - 2 = 2 m + t \end{array}$
Löse das lineare Gleichungssysten zum Beispiel mit dem Additionsverfahren.
Multipliziere dafür zunächst die Gleichung $1)$ auf beiden Seiten mit $(- 1)$
$\begin{array}{l} 1) - 3,5 = m - t \\ 2) - 2 = 2 m + t \end{array}$
Berechne $1) + 2)$
$- 5,5$ $=$ $3 m$
$- \frac{11}{2}$ $=$ $3 m$ $: 3$
$- \frac{11}{2 \cdot 3}$ $=$ $m$
$- \frac{11}{6}$ $=$ $m$
Setze $m$ in eine der beiden Gleichungen ein
$- 2$ $=$ $2 \cdot (- \frac{11}{6}) + t$
$- 2$ $=$ $- \frac{11}{3} + t$ $+ \frac{11}{3}$
$- \frac{6}{3} + \frac{11}{3}$ $=$ $t$
$- \frac{5}{3}$ $=$ $t$
Setze m und t in die allgemeine Geradengleichung.
$m = - \frac{11}{6}; t = \frac{5}{3}$
$y = - \frac{11}{6} \cdot x + \frac{5}{3}$
Die Gerade durch $P_{1}$ und $P_{2}$ ist keine Ursprungsgerade, da für $x = 0$ der y-Wert gleich $\frac{5}{3}$ ist.
15
Stelle die Gleichung der Geraden auf, die durch den Punkt $P (- 3 | 3)$ verläuft und die Steigung $m = - 2$ hat. Zeichne die Gerade.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
1. Setze $m$ und die Koordinaten des Punktes $P$ in die allgemeine Geradengleichung ein und löse nach $t$ auf.
$\begin{array}{l} \begin{array}{ccccc} y & = & m \cdot x + t \\ 3 & = & (- 2) \cdot (- 3) + t & | - 6 \\ 3 - 6 & = & t \end{array} \\ \begin{array}{ccc} t & = & - 3 \end{array} \end{array}$
2. Setze $m$ und $t$ in die allgemeine Geradengleichung ein $\Rightarrow y = - 2 x - 3$
Gerade zeichnen
Zeichne den gegebenen Punkt $P (- 3 | 3)$ in das Koordinatensystem ein. Zeichne dann ein Steigungsdreieck, indem Du um $1$ nach rechts und um $2$ nach unten gehst $(m = - 2)$ . Trage dort den Punkt $Q$ ab. Verbinde $P$ und $Q$ zu einer Geraden.
16
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Zwei Geraden $f (x)$ und $g (x)$ schneiden sich auf der x-Achse in x=4.
Bestimmen Sie mögliche Funktionsterme.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Für diese Aufgabe gibt es keine eindeutige Lösung. Gesucht sind zwei verschiedenen lineare Funktionen, die beide durch den Punkt (4|0) laufen.
Ein sehr einfaches Beispiel wäre $f (x) = 0$ , also die x-Achse und $g (x) = x - 4$ . $f (x)$ läuft offensichtlich durch (4|0). Für g(x) lässt sich das auch sehr einfach überprüfen: $g (4) = 4 - 4 = 0$ .
Andere mögliche Funktionen sind: $y = - x + 4$ , $y = 2 x - 8$ (allgemein $y = a x - 4 a$ für beliebige a)
Überlege durch welchen Punkt beide Geraden gehen müssen.
Bestimme zwei verschiedene Funktionen, die durch diesen Punkt gehen.
17
Funktiongleichung bestimmen.
Eine Gerade hat den y-Achsenabschnitt $t$ und verläuft durch den Punkt $P$ . Bestimmen Sie die Funktionsgleichung f(x) und zeichnen Sie den Graphen.
$t = - 1$ $P = (2 | 3)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung der Funktionsgleichung
Allgemeine Geradengleichung:
$y = m \cdot x + t$
Setze $t$ in die Geradengleichung ein.
$f (x) = m \cdot x - 1$
Setze nun den Punkt $P$ in $f (x)$ ein.
$3 = m \cdot 2 - 1$
Löse nach m auf.
$m = (3 + 1) : 2 = 2$
$f (x) = 2 x - 1$
Zeichnung:

$t = 3$ $P (- 4 | - 3)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Bestimmung der Funktionsgleichung
Allgemeine Geradengleichung:
$y = m \cdot x + t$
Setze $t$ in die Geradengleichung ein.
$f (x) = m \cdot x + 3$
Setze nun den Punkt $P$ in $f (x)$ ein.
$- 3 = m \cdot (- 4) + 3$
Löse nach $m$ auf.
$m = \frac{- 6}{- 4} = \frac{3}{2}$
$f (x) = \frac{3}{2} x + 3$
Zeichnung:
18
Stelle die Gleichung der Geraden durch die zwei Punkte auf und zeichne sie.
$P (2 | 0)$ und $Q (- 2 | 2)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Geradengleichung ermitteln
$P (2 | 0); Q (- 2 | 2)$
Ermittle die Steigung $m$ der allgemeinen Geradengleichung $y = m \cdot x + t$ mithilfe des Differenzenqotienten .
$m = \frac{2 - 0}{- 2 - 2} = \frac{2}{- 4} = - \frac{1}{2}$
Setze $m$ und die Koordinaten eines Punktes z. B. $P (2 | 0)$ in die allgemeine Geradengleichung ein und löse nach $t$ auf.
$0 = - \frac{1}{2} \cdot 2 + t | + \frac{1}{2} \cdot 2$
$t = 1$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
$\Rightarrow$ $y = - \frac{1}{2} x + 1$
Gerade zeichnen
Zeichne die beiden vorgegebenen Punkte $P (2 | 0)$ und $Q (- 2 | 2)$ in das Koordinatensystem ein und verbinde sie zu einer Geraden.

$P (0,5 | 1,5)$ und $Q (5 | 3)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Geradengleichung ermitteln
$P (0,5 | 1,5); Q (5 | 3)$
Ermittle die Steigung $m$ der allgemeinen Geradengleichung $y = m \cdot x + t$ mithilfe des Differenzenqotienten.
$m = \frac{3 - 1,5}{5 - 0,5} = \frac{1,5}{4,5} = \frac{1}{3}$
Setze $m$ und die Koordinaten eines Punktes z. B. $Q (5 | 3)$ in die allgemeine Geradengleichung ein und löse nach $t$ auf.
$3 = \frac{1}{3} \cdot 5 + t | - \frac{1}{3} \cdot 5$
$t = \frac{4}{3}$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
$\Rightarrow$ $y = \frac{1}{3} x + \frac{4}{3}$
Gerade zeichnen
Zeichne die beiden vorgegebenen Punkte $P (0,5 | 1,5)$ und $Q (5 | 3)$ in das Koordinatensystem ein und verbinde sie zu einer Geraden.

$P (- 2 | 1)$ und $Q (6 | 4)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Geradengleichung ermitteln
$P (- 2 | 1)$ ; $Q (6 | 4)$
Ermittle die Steigung $m$ der allgemeinen Geradengleichung $y = m \cdot x + t$ mithilfe des Differenzenqotienten .
$m = \frac{4 - 1}{6 - (- 2)} = \frac{3}{8}$
Setze $m$ und die Koordinaten eines Punktes z. B. $P (- 2 | 1)$ in die allgemeine Geradengleichung ein und löse nach $t$ auf.
$1 = \frac{3}{8} \cdot (- 2) + t$
$1 = - \frac{6}{8} + t$
$1 = - \frac{3}{4} + t | + \frac{3}{4}$
$t = \frac{7}{4}$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
$\Rightarrow$ $y = \frac{3}{8} x + \frac{7}{4}$
Gerade zeichnen
Zeichne die beiden vorgegebenen Punkte $P (- 2 | 1)$ und $Q (6 | 4)$ in das Koordinatensystem ein und verbinde sie zu einer Geraden.

$P (- 4 | 1)$ und $Q (1 | - 1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Geradengleichung ermitteln
$P (- 4 | 1)$ ; $Q (1 | - 1)$
Ermittle die Steigung $m$ der allgemeinen Geradengleichung $y = m \cdot x + t$ mithilfe des Differenzenqotienten.
$m = \frac{- 1 - 1}{1 - (- 4)} = - \frac{2}{5}$
Setze $m$ und die Koordinaten eines Punktes z. B. $P (- 4 | 1)$ in die allgemeine Geradengleichung ein und löse nach $t$ auf.
$1 = - \frac{2}{5} \cdot (- 4) + t$
$1 = \frac{8}{5} + t | - \frac{8}{5}$
$t = - \frac{3}{5}$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
$\Rightarrow$ $y = - \frac{2}{5} x - \frac{3}{5}$
Gerade zeichnen
Zeichne die beiden vorgegebenen Punkte $P (- 4 | 1)$ und $Q (1 | - 1)$ in das Koordinatensystem ein und verbinde sie zu einer Geraden.
19
Gegeben sind der $y$ -Achsenabschnitt $t = 2$ und der Punkt $P (3 | - 1)$ . Berechne die zugehörende Geradengleichung und zeichne die Gerade.
ist die Gleichung der Geraden.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
1. Setze $t$ und die Koordinaten des Punktes $P$ in die allgemeine Geradengleichung ein und löse nach $m$ auf.
$\begin{array}{l} \begin{array}{ccccc} y & = & m \cdot x + t \\ - 1 & = & m \cdot 3 + 2 & | - 2 \\ - 1 - 2 & = & m \cdot 3 | : 3 \end{array} \\ \begin{array}{ccc} m = \frac{- 3}{3} = - 1 \end{array} \end{array}$
2. Setze $m$ und $t$ in die allgemeine Geradengleichung ein $\Rightarrow y = - x + 2$
Gerade zeichnen
Zeichne den gegebenen Punkt $P (3 | - 1)$ in das Koordinatensystem ein. Zeichne dann den Punkt $S_{y} (0 | 2)$ ( $y$ -Achsenabschnitt $t = 2$ ) ebenfalls ein und verbinde die Punkte $S_{y}$ und $P$ zu einer Geraden.
20
Gegeben sind die Punkte $A (40 | 220), B (100 | 250), C (200 | 300), D (80 | 240)$ .
Zeichne die Punkte $A - D$ in ein geeignetes Koordinatensystem ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung

Bestimme die Geradengleichung der durch die Punkte $A - D$ verlaufenden Gerade.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Betrachte $A (40 | 220)$ und $B (100 | 250)$ .
Wähle aus $A$ : $x_{1} = 40$ und $y_{1} = 220$ und von $B$ : $x_{2} = 100$ und $y_{2} = 250$ .
$m = \frac{Δ y}{Δ x} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{250 - 220}{100 - 40} = \frac{30}{60} = 0,5$
Da die Punkte $A - D$ alle auf einer Geraden liegen, reicht es, wenn du dir nur zwei Punkte (beispielsweise $A$ und $B$ ) heraussuchst. Mit deren Hilfe bestimmst du die Steigung der Gerade. Hierfür ziehst du die y-Koordinate vom Punkt $A$ von der y-Koordinate vom Punkt $B$ ab, und die x-Koordinate vom Punkt $A$ von der x-Koordinate vom Punkt $B$ .
Nun wird der y-Achsenabschnitt bestimmt, indem man einen Punkt auf der Gerade (zum Beispiel $C$ ), in die Geradengleichung $\begin{array}{l} y = m x + t \end{array}$ einsetzt und nach $t$ auflöst.
Setze Punkt $C$ in die Geradengleichung $y = m x + t$ ein, wobei wir das zuvor berechnete $m = 0,5$ einsetzen:
$y$ $=$ $0,5 \cdot x + t$
$300$ $=$ $0,5 \cdot 200 + t$
$\Leftrightarrow t$ $=$ $200$
Damit haben wir sowohl $m$ als auch $t$ bestimmt, so dass unsere Geradengleichung lautet:
$y = 0,5 \cdot x + 200$

Gib drei weitere Punkte an, die auf der Gerade liegen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Setze drei beliebige x-Werte in die Geradengleichung ein, um den jeweiligen y-Wert zu bekommen, z.B. $x_{1} = 0, x_{2} = - 100$ und $x_{3} = 300$ .
$y$ $=$ $0,5 \cdot x + 200$
$y_{1}$ $=$ $0,5 \cdot x_{1} + 200$
$=$ $0,5 \cdot 0 + 200 = 200$
$y_{2}$ $=$ $0,5 \cdot x_{2} + 200$
$=$ $0,5 \cdot (- 100) + 200 = 150$
$y_{3}$ $=$ $0,5 \cdot x_{3} + 200$
$=$ $0,5 \cdot 300 + 200 = 350$
Damit erhalten wir also folgende drei Punkte $D, E$ und $F$ :
$D (0 | 200), E (- 100 | 150)$ und $F (300 | 350)$
21
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Für eine lineare Funktion $h (x)$ gilt:
$h (0) = 3$ und $h (- 2) = 4$ . Bestimmen Sie $h (x)$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichungen
Bestimme den y-Achsenabschnitt t
Bei einer Funktion ist der y-Achsenabschnitt gleich dem Wert bei x=0.
$t = h (0) = 3$
Bestimme jetzt mit den zwei gegebenen Punkten die Steigung m mit dem Differenzenquotienten.
$m = \frac{3 - 4}{0 - (- 2)} = \frac{- 1}{2} = - \frac{1}{2}$
Setze zur Geradengleichung zusammen.
$\Rightarrow y = - \frac{1}{2} x + 3$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$0$	$=$	$3 \cdot 1 + t$	$- 3$
	↓	Gleichung nach t auflösen.
$t$	$=$	$- 3$

$18$	$=$	$4 \cdot 5 + t$	$- 20$
	↓	Gleichung nach t auflösen.
$t$	$=$	$- 2$

$4$	$=$	$- 2 \cdot (- 1) + t$	$- 2$
	↓	Gleichung nach t auflösen.
$t$	$=$	$2$

$m$	$=$	$\frac{8 - 7}{- 3 - 5}$
	↓	Vereinfache Zähler und Nenner
$m$	$=$	$\frac{1}{- 8}$
$m$	$=$	$- \frac{1}{8}$

$m$	$=$	$\frac{4 - 2}{3 - 1}$
	↓	Vereinfache Zähler und Nenner
$m$	$=$	$\frac{2}{2}$
$m$	$=$	$1$

$f (x)$	$=$	$a_{1} \cdot x + t$
	↓	Setze $a_{1} = \frac{1}{2}$ in die allgemeine Geradengleichung ein.
$f (x)$	$=$	$\frac{1}{2} x + t$
	↓	Setze P in f(x) ein.
$- 2$	$=$	$\frac{1}{2} \cdot 4 + t$	$- 2$
	↓	löse nach t auf
$t$	$=$	$- 4$
	↓	Setze t in f(x) ein.

$f (x)$	$=$	$0$
	↓	Gesucht ist hier ein x mit f(x) =0 und somit y=0 ist. Setze Funktionsgleichung gleich 0.
$\frac{1}{2} x - 4$	$=$	$0$	$+ 4$
$\frac{1}{2} x$	$=$	$4$	$: \frac{1}{2}$
$x$	$=$	$\frac{4}{\frac{1}{2}}$
	↓	Du dividierst durch einen Bruch $\to$ Multipliziere mit dem Kehrwert.
$x$	$=$	$4 \cdot 2$
$x$	$=$	$8$

$f (x)$	$=$	$a_{1} \cdot x + t$
	↓	t: y-Achsenabschnitt Setze $a_{2} = \frac{3}{4}$ in die allgemeine Geradengleichung ein.
$f (x)$	$=$	$\frac{3}{4} x + t$
	↓	Setze P(1/-3) in f(x) ein.
$- 3$	$=$	$\frac{3}{4} \cdot 1 + t$
	↓	Multipliziere
$- 3$	$=$	$\frac{3}{4} + t$	$- \frac{3}{4}$
$t$	$=$	$- 3 - \frac{3}{4}$
	↓	Addiere
$t$	$=$	$- 3,75$
	↓	Setze t in f(x) ein.

$\frac{3}{4} x - 3,75$	$=$	$0$	$+ 3,75$
$\frac{3}{4} x$	$=$	$3,75$	$: \frac{3}{4}$
$x$	$=$	$3,75 : \frac{3}{4}$
	↓	Du dividierst durch einen Bruch $\to$ Multipliziere mit dem Kehrwert.
$x$	$=$	$3,75 \cdot \frac{4}{3}$
	↓	Multiplikation
$x$	$=$	$5$

$f (x)$	$=$	$a_{1} \cdot x + t$
	↓	t: y-Achsenabschnitt Setze $a_{3} = 2$ in die allgemeine Geradengleichung ein.
$f (x)$	$=$	$2 x + t$
	↓	Setze P(3/-1) in f(x) ein.
$- 1$	$=$	$2 \cdot 3 + t$
	↓	Multipliziere
$- 1$	$=$	$6 + t$	$- 6$
$t$	$=$	$- 1 - 6$
	↓	Subtrahiere
$t$	$=$	$- 7$
	↓	Setze t in f(x) ein.

$\frac{4}{5} x + 2,8$	$=$	$0$	$- 2,8$
$\frac{4}{5} x$	$=$	$- 2,8$	$: \frac{4}{5}$
$x$	$=$	$- 2,8 : \frac{4}{5}$
	↓	Dividiere
$x$	$=$	$- \frac{7}{2}$
$x$	$=$	$- 3,5$

$- \frac{2}{3} x + 1 \frac{2}{3}$	$=$	$0$	$- 1 \frac{2}{3}$
$- \frac{2}{3} x$	$=$	$- 1 \frac{2}{3} = - \frac{5}{3}$	$: (- \frac{2}{3})$
$x$	$=$	$\frac{- \frac{5}{3}}{- \frac{2}{3}}$
	↓	Brüche dividieren.
$x_{N}$	$=$	$- \frac{5}{3} \cdot (- \frac{3}{2})$
	$=$	$\frac{5}{2} = 2,5$

$\frac{11}{2}$	$=$	$- 7 m$	$: (- 7)$
$m$	$=$	$\frac{\frac{11}{2}}{- 7}$
$m$	$=$	$- \frac{11}{14}$

$- 1$	$=$	$- \frac{11}{14} \cdot 4 + t$
$- 1$	$=$	$- \frac{44}{14} + t$	$+ \frac{44}{14}$

$2 x - 7$	$=$	$0$	$+ 7$
$2 x$	$=$	$7$	$: 2$
$x$	$=$	$7 : 2$
	↓	Dividiere
$x$	$=$	$3,5$

$f (x)$	$=$	$a_{1} \cdot x + t$
	↓	t: y-Achsenabschnitt Setze $a_{4} = \frac{4}{5}$ in die allgemeine Geradengleichung ein.
$f (x)$	$=$	$\frac{4}{5} x + t$
	↓	Setze $P (\frac{3}{2} \| 4)$ in f(x) ein.
$4$	$=$	$\frac{4}{5} \cdot \frac{3}{2} + t$
	↓	Kürze den Bruch mit 2.
$4$	$=$	$\frac{2}{5} \cdot 3 + t$
	↓	Multipliziere
$4$	$=$	$\frac{6}{5} + t$	$- \frac{6}{5}$
$t$	$=$	$4 - \frac{6}{5}$
	↓	Schreibe 4 als Bruch mit 4 im Nenner.
$t$	$=$	$\frac{20}{5} - \frac{6}{5}$
	↓	Subtrahiere
$t$	$=$	$\frac{14}{5}$
$t$	$=$	$2,8$
	↓	Setze t in f(x) ein.

$- 3$	$=$	$m \cdot 2 + 3$	$- 3$
$- 6$	$=$	$m \cdot 2$	$: 2$
$- 3$	$=$	$m$

$1) - 2) - 5$	$=$	$- 5 m$	$: (- 5)$
$m$	$=$	$1$
	↓	Setze m in 2) ein.
$3$	$=$	$2 + t$	$- 2$
$t$	$=$	$1$
	↓	Setze m und t in die allgemeine Geradengleichung ein.
$y$	$=$	$x + 1 \Rightarrow f (x) = x + 1$

1) - 2)
	↓
$4$	$=$	$- 6 m$	$: (- 6)$
$m$	$=$	$\frac{4}{- 6}$
	↓	Kürze mit 2.
$m$	$=$	$- \frac{2}{3}$
	↓	Setze m in 1) ein
$3$	$=$	$- 2 (- \frac{2}{3}) + t$
	↓	Multipliziere.
$3$	$=$	$\frac{4}{3} + t$	$- \frac{4}{3}$
$t$	$=$	$3 - \frac{4}{3}$
	↓	Subtrahiere.
$t$	$=$	$1 \frac{2}{3}$
	↓	Setze m und t in die allg. Geradengleichung ein.
$y$	$=$	$- \frac{2}{3} x + 1 \frac{2}{3}$

$\frac{2}{7} x + \frac{1}{7}$	$=$	$0$	$- \frac{1}{7}$
$\frac{2}{7} x$	$=$	$- \frac{1}{7}$	$: \frac{2}{7}$
$x$	$=$	$\frac{- \frac{1}{7}}{\frac{2}{7}}$
	↓	Dividiere die Brüche. $\to$ Multipliziere mit dem Kehrwert.
$x$	$=$	$- \frac{1}{7} \cdot \frac{7}{2}$
$x_{N}$	$=$	$- \frac{1}{2}$

$- \frac{11}{14} x + \frac{30}{14}$	$=$	$0$	$- \frac{30}{14}$
$- \frac{11}{14} x$	$=$	$- \frac{30}{14}$	$: (- \frac{11}{14})$
	↓	Dividiere die Brüche. Das heißt multipliziere mit dem Kehrbruch.
$x$	$=$	$- \frac{30}{14} \cdot (- \frac{14}{11})$
$x_{N}$	$=$	$\frac{30}{11}$

$- 6$	$=$	$- 7,5 m$	$: (- 7,5)$
$m$	$=$	$\frac{- 6}{- 7,5}$
$m$	$=$	$0,8$
	↓	Setze $m$ in $1)$ ein.
$- 2$	$=$	$0,8 \cdot (- 4) + t$
$- 2$	$=$	$- 3,2 + t$	$+ 3,2$

$0,8 x + 1,2$	$=$	$0$	$- 1,2$
$0,8 x$	$=$	$- 1,2$	$: 0,8$
$x$	$=$	$\frac{- 1,2}{0,8}$

$30$	$=$	$\frac{75}{4} + t$	$- \frac{75}{4}$
	↓	Löse nach t auf.
$t$	$=$	$30 - \frac{75}{4}$
$t$	$=$	$\frac{45}{4}$
	↓	Setze m und t in die allgemeine Geradengleichung ein.

Aufgaben zum Aufstellen von Geradengleichungen

Geradengleichung aufstellen

Gleichung aufstellen

Gleichung aufstellen

Gleichung aufstellen

Bestimmung der Funktionsgleichung

Bestimmung des Schnittpunkts mit der y-Achse

Bestimmung des Schnittpunkts mit der x-Achse

Zeichnung

Bestimmung der Funktionsgleichung

Bestimmung der Achsenschnittpunkte

Zeichung

Bestimmung der Funktionsgleichung

Bestimmung der Achsenschnittpunkte

Zeichnung

Bestimmung der Funktionsgleichung

Bestimmung der Achsenschnittpunkte

Zeichnung

Bestimmung der Funktionsgleichung

Bestimmung der Achsenschnittpunkte

Zeichnung

Bestimmung der Funktionsgleichung

Bestimmung der Achsenschnittpunkte

Zeichnung

Bestimmung der Funktionsgleichung

Bestimmung der Achsenschnittpunkte

Zeichnung

Bestimmung der Funktionsgleichung

Bestimmung der Achsenschnittpunkte

Zeichnung

Bestimmung der Funktionsgleichung

Bestimmung der Achsenschnittpunkte

Zeichnung

Bestimmung der Funktionsgleichung

Bestimmung der Achsenschnittpunkte

Zeichnung

Steigung

Funktionsgleichung

Bestimmung der Steigung m

Ermittlung des y-Achsenabschnitts t

Funktionsterm aufstellen

Gerade zeichnen

Funktionsterm aufstellen

Gerade zeichnen

Funktionsterm aufstellen

Gerade zeichnen

Funktionsterm aufstellen

Gerade zeichnen

Geradengleichung erstellen

Gerade zeichnen

Gerade zeichnen

Bestimmung der Funktionsgleichung

Bestimmung der Funktionsgleichung

Geradengleichung ermitteln

Gerade zeichnen

Geradengleichung ermitteln

Gerade zeichnen

Geradengleichung ermitteln

Gerade zeichnen

Geradengleichung ermitteln

Gerade zeichnen

Gerade zeichnen

Bestimmung der Steigung $m$

Ermittlung des $y$ -Achsenabschnitts $t$

$- \frac{1}{2}$	$=$	$- \frac{4}{3} \cdot (- 2) + t$
	↓	$- \frac{4}{3} \cdot (- 2) = \frac{(- 4) \cdot (- 2)}{3} = \frac{8}{3}$
$- \frac{1}{2}$	$=$	$\frac{8}{3} + t$	$- \frac{8}{3}$
$t$	$=$	$- \frac{1}{2} - \frac{8}{3}$
	↓	Bringe die beiden Brüche auf denselben Nenner.
$t$	$=$	$- \frac{3}{6} - \frac{16}{6}$
	↓	Subtrahiere.
$t$	$=$	$- \frac{19}{6}$
	↓	Wandle in einen gemischten Bruch um.
$t$	$=$	$- 3 \frac{1}{6}$
	↓	Setze t und m in die allgemeine Geradengleichung ein.

$4$	$=$	$2 \cdot 2 + t$
$4$	$=$	$4 + t$	$- 4$
$t$	$=$	$4 - 4$
$t$	$=$	$0$

$- 5,5$	$=$	$3 m$
$- \frac{11}{2}$	$=$	$3 m$	$: 3$
$- \frac{11}{2 \cdot 3}$	$=$	$m$
$- \frac{11}{6}$	$=$	$m$

$- 2$	$=$	$2 \cdot (- \frac{11}{6}) + t$
$- 2$	$=$	$- \frac{11}{3} + t$	$+ \frac{11}{3}$
$- \frac{6}{3} + \frac{11}{3}$	$=$	$t$
$- \frac{5}{3}$	$=$	$t$

$y$	$=$	$0,5 \cdot x + t$
$300$	$=$	$0,5 \cdot 200 + t$
$\Leftrightarrow t$	$=$	$200$

$y_{1}$	$=$	$0,5 \cdot x_{1} + 200$
	$=$	$0,5 \cdot 0 + 200 = 200$

$y_{2}$	$=$	$0,5 \cdot x_{2} + 200$
	$=$	$0,5 \cdot (- 100) + 200 = 150$

$y_{3}$	$=$	$0,5 \cdot x_{3} + 200$
	$=$	$0,5 \cdot 300 + 200 = 350$