Schnittpunkte mit den Koordinatenachsen

Wenn die Funktion $f\left(x\right)$ die $x$-Achse schneidet, ist der $y$-Wert an diesen Stellen gleich null. Die Schnittpunkte von $f$ mit der $x$-Achse entsprechen also den Nullstellen von $f$.

Die Koordinaten des Schnittpunkts mit der $x$-Achse sind dann allgemein: $S\left(x|0\right)$.

Um die Schnittpunkte einer Funktion $f\left(x\right)$ mit der $x$-Achse zu berechnen, musst du daher den y-Wert gleich null setzen. Anschließend löst du die Gleichung nach x auf.

Beispiel:

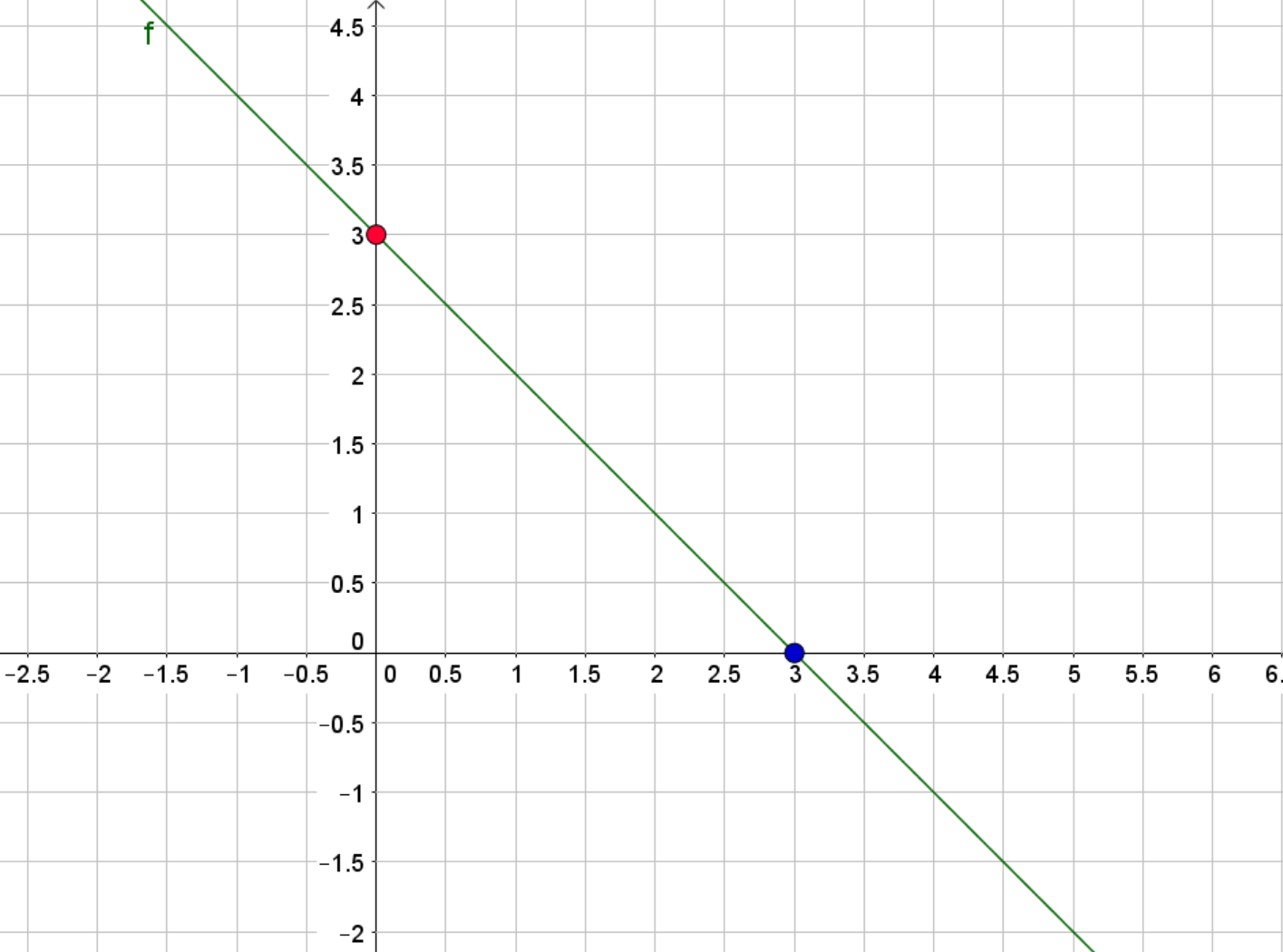
Wir wollen berechnen, in welchem Punkt die Gerade $y=2x-4$ die $x$-Achse schneidet. Anders gesagt: Wir wollen die Nullstellen der Geraden berechnen.

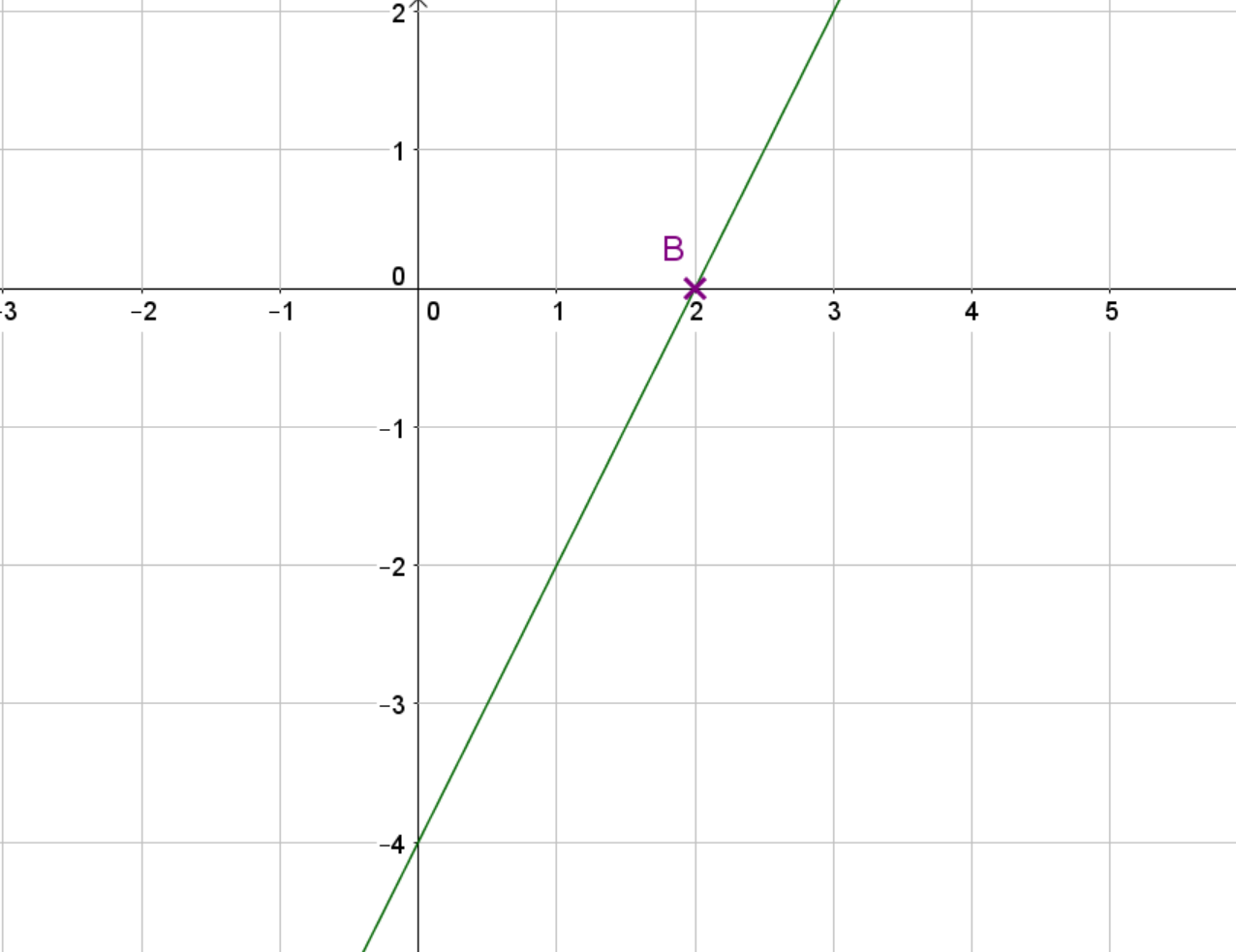
Wie du an der Abbildung erkennen kannst, ist $B$ der Punkt, in dem die Gerade die $x$-Achse schneidet. Die $y$-Koordinate von $B$ ist gleich null: $y=0$.

Um zu berechnen, was die $x$-Koordinate von $B$ ist, kannst du die Geradengleichung daher gleich Null setzen, also $y=0$.

$2x-4=0$

Diese Gleichung kannst du jetzt nach $x$ auflösen:

Die $x$-Koordinate von $B$ ist also $x=2$. Das kannst du auch oben am Graphen überprüfen. Die Gerade hat also eine Nullstelle bei $x=2$

Die Gerade schneidet die $x$-Achse im Punkt $B\left(2|0\right)$.

Beispiel:

Der Graph zeigt die Funktion $f\left(x\right)=x^3-x$.

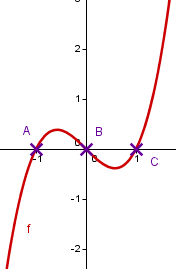
Alternativ kannst du auch das $f\left(x\right)$ durch $y$ ersetzen, also $y=x^3-x$ schreiben.

Wir wollen die Schnittpunkte von $f$ mit der $x$-Achse, also die Nullstellen von $f$ berechnen. Deshalb setzen wir $y$ gleich null: $y=0$

$x^3-x=0$

Diese Gleichung müssen wir nun nach $x$ auflösen. Dafür können wir zunächst ein $x$ ausklammern:

$x(x^2-1)=0$

Der Term in Klammern $(x^2-1)$ erinnert uns an die 3. binomische Formel: $(x^2-1)=(x+1)(x-1)$. Wenn wir diese anwenden, können wir die Nullstellen von $f$ leichter ablesen:

$x(x+1)(x-1)=0$

Ein Produkt ist immer genau dann null, wenn einer seiner Faktoren null wird. Deshalb können wir die Schnittpunkte von $f$ ablesen:

$\underset{x_1=0}{\underbrace{x}}(\underset{x_2=-1}{\underbrace{x+1}})(\underset{x_3=1}{\underbrace{x-1}})=0$

Setzt man also beispielsweise in die erste Klammer $(x+1)$ für $x=-1$ ein, wird diese Klammer null. Damit wird das gesamte Produkt null.

An den Punkten, an denen die Funktion $f\left(x\right)$ die $y$-Achse schneidet, ist der $x$-Wert gleich null.

Die Koordinaten des Schnittpunkts mit der $y$-Achse sind dann allgemein: $S\left(0|y\right)$.

Um die Schnittpunkte einer Funktion $f\left(x\right)$ mit der $y$-Achse zu berechnen, musst du deswegen für $x$ null einsetzen, also $f\left(0\right)$ ausrechnen.

Beispiel:

Wir berechnen für die obige Gerade $y=2x-4$ jetzt die Schnittpunkte mit der $y$-Achse.

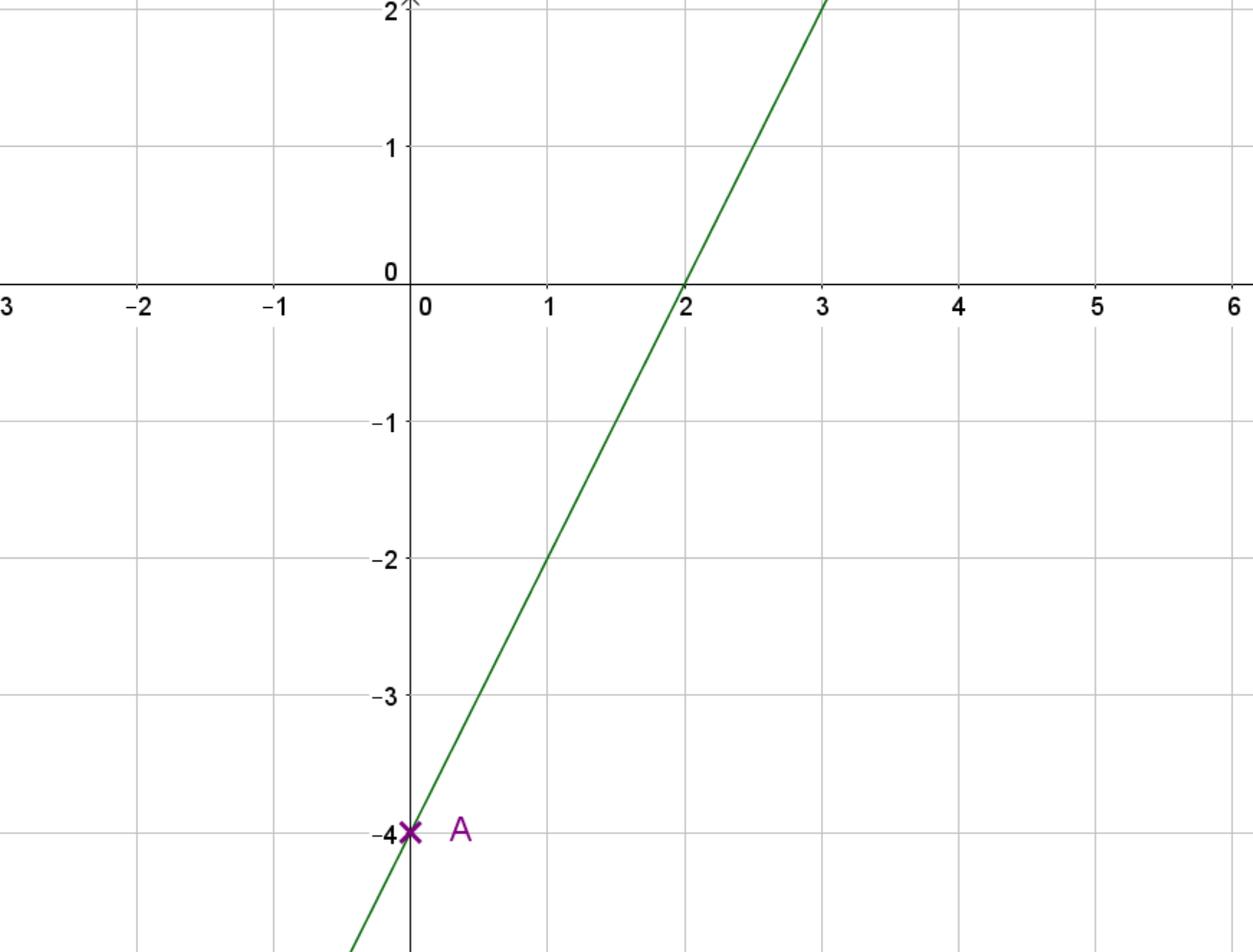
Wie du in der Abbildung sehen kannst, schneidet die Gerade die $y$-Achse im Punkt $A$. Die $x$-Koordinate von $A$ ist null: $x=0$

Um jetzt die $y$-Koordinate von $A$ zu berechnen, setzen wir deshalb für $x$ null ein und rechnen $y$ aus:

$y=2\cdot 0-4=0-4=-4$

Die $y$-Koordinate von $A$ ist also $-4$. Das ist auch der $y$-Achsenabschnitt der Gerade. Im Fall einer Gerade $g\left(x\right)=mx+t$ kannst du den $y$-Achsenabschnitt auch direkt an der Funktionsgleichung ablesen: $t$ ist der $y$-Achsenabschnitt.

Unsere Gerade schneidet die $y$-Achse also im Punkt $A(0|-4)$.

Beispiel:

Wir wollen für die obige Funktion $f(x)=x^3-x$ nun auch die Schnittpunkte mit der $y$-Achse berechnen.

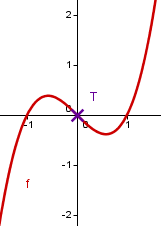
Dafür berechnen wir $f\left(0\right)$:

$f\left(0\right)=0^3-0=0$