Winkelhalbierende
Die Winkelhalbierende eines Winkels ist ein Strahl, der im Scheitelpunkt eines Winkels entspringt und den Winkel in zwei gleiche Teile teilt.
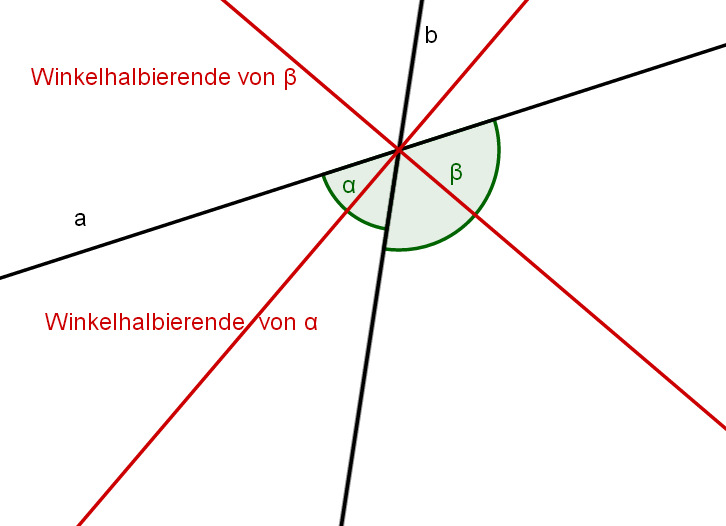
Ein sich schneidendes Geradenpaar bestimmt zwei Winkelhalbierende, die zueinander orthogonal sind. Hier im Bild schneiden sich die Geraden und in den Winkeln und .
Die Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt, der gleichzeitig der Mittelpunkt des Inkreis ist.
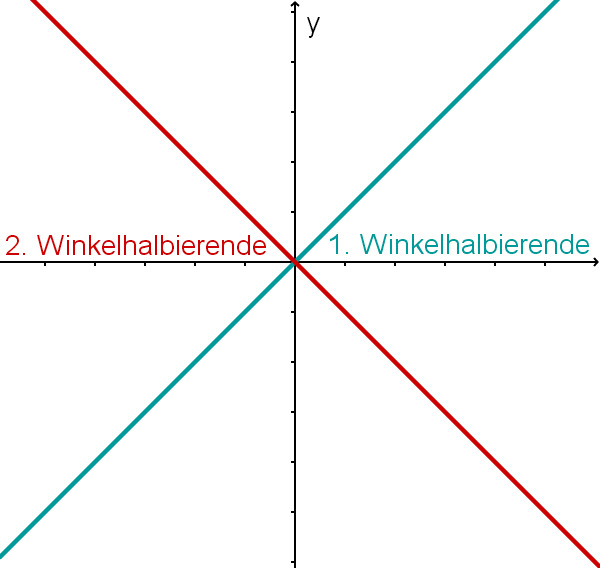
Erste und zweite Winkelhalbierende
In einem kartesischen Koordinatensystem sind die beiden Winkelhalbierenden Geraden, wie im Bild rechts definiert.
Konstruktion
Die Winkelhalbierende kann mit einem Zirkel und einem Lineal (Geodreieck) konstruiert werden:
Dabei wird um den Scheitelpunkt des Winkels (bzw. im Fall zweier sich schneidender Geraden um den Schnittpunkt) ein Kreis mit beliebigem Radius gezeichnet.
An den Schnittpunkten mit den Schenkeln des Winkels wird der Zirkel erneut angesetzt. Dann zeichnet man jeweils einen Kreis mit gleichem Radius.
Die Schnittpunkte dieser zwei Kreise liegen auf der Winkelhalbierenden.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:



