Aufgaben zur Spiegelung in der analytischen Geometrie

Spieglein, Spieglein - Lerne mit diesen gemischten Übungsaufgaben das Spiegeln von Punkten, Geraden und Ebenen!

1
Spiegele den Punkt $P (1 | 2 | 5)$ am Punkt $Z$ .
$Z (1 | 3 | - 4)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung Punkt an Punkt
Der Punkt $P (1 | 2 | 5)$ wird am Punkt $Z (1 | 3 | - 4)$ gespiegelt.
$\vec{O P} = (\begin{array}{c} 1 \\ 2 \\ 5 \end{array})$ und $\vec{O Z} = (\begin{array}{c} 1 \\ 3 \\ - 4 \end{array})$
Berechne den Vektor:
$\vec{P Z} = \vec{O Z} - \vec{O P} = (\begin{array}{c} 1 \\ 3 \\ - 4 \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) = (\begin{array}{c} 0 \\ 1 \\ - 9 \end{array})$ .
Setze die Vektoren in $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P Z}$ ein:
$\vec{O P^{'}} = (\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) + 2 \cdot (\begin{array}{c} 0 \\ 1 \\ - 9 \end{array}) = (\begin{array}{c} 1 \\ 4 \\ - 13 \end{array})$
Antwort: Der gespiegelte Punkt $P^{'}$ hat die Koordinaten $P^{'} (1 | 4 | - 13)$ .
Benutze zur Berechnung des Spiegelpunktes die Vektorgleichung:
$\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P Z}$

$Z (- 1 | 3 | 1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung Punkt an Punkt
Der Punkt $P (1 | 2 | 5)$ wird am Punkt $Z (- 1 | 3 | 1)$ gespiegelt.
$\vec{O P} = (\begin{array}{c} 1 \\ 2 \\ 5 \end{array})$ und $\vec{O Z} = (\begin{array}{c} - 1 \\ 3 \\ 1 \end{array})$
Berechne den Vektor:
$\vec{P Z} = \vec{O Z} - \vec{O P} = (\begin{array}{c} - 1 \\ 3 \\ 1 \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) = (\begin{array}{c} - 2 \\ 1 \\ - 4 \end{array})$ .
Setze die Vektoren in $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P Z}$ ein:
$\vec{O P^{'}} = (\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) + 2 \cdot (\begin{array}{c} - 2 \\ 1 \\ - 4 \end{array}) = (\begin{array}{c} - 3 \\ 4 \\ - 3 \end{array})$
Antwort: Der gespiegelte Punkt $P^{'}$ hat die Koordinaten $P^{'} (- 3 | 4 | - 3)$ .
Benutze zur Berechnung des Spiegelpunktes die Vektorgleichung:
$\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P Z}$

Spiegele den Punkt $P (1 | 2 | 5)$ an der Geraden

$g : \vec{x} = (\begin{array}{c} 1 \\ 2 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})$

$h : \vec{x} = (\begin{array}{c} - 2 \\ 1 \\ 3 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array})$

Spiegele den Punkt $P (1 | 2 | 5)$ an der Ebene.

$E : x_{1} + 3 x_{2} - 2 x_{3} = 11$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Ebene spiegeln
1. Hilfsgerade $h$ aufstellen, die senkrecht zur Ebene $E$ steht (der Normalenvektor ${\vec{n}}_{E} = (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$ der Ebene ist der Richtungsvektor der Geraden $h$ und verläuft durch den Punkt $P (1 | 2 | 5)$ :
$h : \vec{x} = (\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
2. Schnittpunkt $S$ der Gerade $h$ mit der Ebene $E$ bestimmen.
$h \cap E$
$x_{1} + 3 x_{2} - 2 x_{3}$ $=$ $11$
↓
Setze $h : \vec{x} = (\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$ in $E$ ein.
$(1 + r) + 3 \cdot (2 + 3 r) - 2 \cdot (5 - 2 r)$ $=$ $11$
↓
Löse die Klammern auf.
$1 + r + 6 + 9 r - 10 + 4 r$ $=$ $11$
↓
Fasse zusammen.
$- 3 + 14 r$ $=$ $11$ $+ 3$
↓
Löse nach r auf.
$14 r$ $=$ $14$ $: 14$
$r$ $=$ $1$
Setze $r = 1$ in $h$ ein, um den Schnittpunkt $S$ zu berechnen:
${\vec{x}}_{S} = (\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) + 1 \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array}) = (\begin{array}{c} 2 \\ 5 \\ 3 \end{array})$ $\Rightarrow S (2 | 5 | 3)$
3. Vektor $\vec{P S}$ berechnen:
$\vec{P S} = \vec{O S} - \vec{O P} = (\begin{array}{c} 2 \\ 5 \\ 3 \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) = (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$
4. Vektor $\vec{P S}$ zu $\vec{O S}$ addieren, um den gesuchten Punkt $P^{'}$ zu bekommen.
$\vec{O P^{'}} = \vec{O S} + \vec{P S} = (\begin{array}{c} 2 \\ 5 \\ 3 \end{array}) + (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array}) = (\begin{array}{c} 3 \\ 8 \\ 1 \end{array})$
Antwort: Der Spiegelpunkt hat die Koordinaten $P^{'} (3 | 8 | 1)$ .

$F : - 2 x_{1} + x_{2} + 3 x_{3} = 43$

4
Spiegele die Gerade $g$ an der Ebene $E$ .
$g : \vec{x} = (\begin{array}{c} 2 \\ 4 \\ 3 \end{array}) + r \cdot (\begin{array}{c} 0 \\ 1 \\ 1 \end{array})$ , $E : 4 x_{1} - 2 x_{2} + 2 x_{3} = 30$ und $g ∥ E$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung einer Geraden an einer Ebene
1. Erstelle die Gleichung einer Lotgeraden $l_{L o t}$ mit dem Aufpunkt $P$ der Geraden $g$ und mit dem Normalenvektor ${\vec{n}}_{E}$ der Ebene $E$ : $l_{L o t} : \vec{x} = \vec{O P} + s \cdot {\vec{n}}_{E} = (\begin{array}{c} 2 \\ 4 \\ 3 \end{array}) + s \cdot (\begin{array}{c} 4 \\ - 2 \\ 2 \end{array})$
2. Schneide die Gerade $l_{L o t}$ mit der Ebene $E$ .
$l_{L o t} \cap E$
$4 x_{1} - 2 x_{2} + 2 x_{3}$ $=$ $30$
↓
Setze $l_{L o t} : \vec{x} = (\begin{array}{c} 2 \\ 4 \\ 3 \end{array}) + s \cdot (\begin{array}{c} 4 \\ - 2 \\ 2 \end{array})$ in $E$ ein.
$4 \cdot (2 + 4 s) - 2 \cdot (4 - 2 s) + 2 \cdot (3 + 2 s)$ $=$ $30$
↓
Löse die Klammern auf.
$8 + 16 s - 8 + 4 s + 6 + 4 s$ $=$ $30$
↓
Fasse zusammen.
$6 + 24 s$ $=$ $30$ $- 6$
$24 s$ $=$ $24$ $: 24$
$s$ $=$ $1$
Setze $s = 1$ in die Lotgeradengleichung $l_{L o t}$ ein, um den Punkt $F$ zu berechnen.
${\vec{x}}_{F} = (\begin{array}{c} 2 \\ 4 \\ 3 \end{array}) + 1 \cdot (\begin{array}{c} 4 \\ - 2 \\ 2 \end{array}) = (\begin{array}{c} 6 \\ 2 \\ 5 \end{array})$ $\Rightarrow F (6 | 2 | 5)$
3. Berechne den Vektor $\vec{P F}$
$\vec{P F} = \vec{O F} - \vec{O P} = (\begin{array}{c} 6 \\ 2 \\ 5 \end{array}) - (\begin{array}{c} 2 \\ 4 \\ 3 \end{array}) = (\begin{array}{c} 4 \\ - 2 \\ 2 \end{array})$
4. Setze $\vec{O P}$ und $\vec{P F}$ in die Vektorgleichung $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F}$ ein:
$\vec{O P^{'}} = (\begin{array}{c} 2 \\ 4 \\ 3 \end{array}) + 2 \cdot (\begin{array}{c} 4 \\ - 2 \\ 2 \end{array}) = (\begin{array}{c} 10 \\ 0 \\ 7 \end{array})$
5. Der berechnete Punkt $P^{'}$ ist der Aufpunkt der Spiegelgeraden $g^{'}$ . Die Spiegelgerade hat den Richtungsvektor $\vec{u}$ (parallele Gerade zu $g$ ) $\Rightarrow g^{'} : \vec{x} = \vec{O P^{'}} + t \cdot \vec{u}$
$A n t w o r t :$ Die gespiegelte Gerade hat die Gleichung $g^{'} : \vec{x} = (\begin{array}{c} 10 \\ 0 \\ 7 \end{array}) + t \cdot (\begin{array}{c} 0 \\ 1 \\ 1 \end{array})$

$g : \vec{x} = (\begin{array}{c} - 1 \\ 2 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 4 \\ 1 \\ 3 \end{array})$ , $E : x_{1} + 2 x_{2} - 3 x_{3} = - 9$ und $g \cap E \Rightarrow S (11 | 5 | 10)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung einer Geraden an einer Ebene
1. Erstelle die Gleichung einer Lotgeraden $l_{L o t}$ mit dem Aufpunkt $P$ der Geraden $g$ und mit dem Normalenvektor ${\vec{n}}_{E}$ der Ebene $E$ : $l_{L o t} : \vec{x} = \vec{O P} + s \cdot {\vec{n}}_{E} = (\begin{array}{c} - 1 \\ 2 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ - 3 \end{array})$
2. Schneide die Gerade $l_{L o t}$ mit der Ebene $E$ .
Setze $l_{L o t} : \vec{x} = (\begin{array}{c} - 1 \\ 2 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ - 3 \end{array})$ in $E$ ein.
$l_{L o t} \cap E$
$x_{1} + 2 x_{2} - 3 x_{3}$ $=$ $- 9$
↓
Setze $l_{L o t} : \vec{x} = (\begin{array}{c} - 1 \\ 2 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ - 3 \end{array})$ in $E$ ein.
$(- 1 + s) + 2 \cdot (2 + 2 s) - 3 \cdot (1 - 3 s)$ $=$ $- 9$
↓
Löse die Klammern auf
$- 1 + s + 4 + 4 s - 3 + 9 s$ $=$ $- 9$
↓
Fasse zusammen.
$14 s$ $=$ $- 9$ $: 14$
$s$ $=$ $- \frac{9}{14}$
Setze $s = - \frac{9}{14}$ in die Lotgeradengleichung $l_{L o t}$ ein, um den Punkt $F$ zu berechnen.
${\vec{x}}_{F} = (\begin{array}{c} - 1 \\ 2 \\ 1 \end{array}) + (- \frac{9}{14}) \cdot (\begin{array}{c} 1 \\ 2 \\ - 3 \end{array}) = (\begin{array}{c} - 1 - \frac{9}{14} \\ 2 - \frac{18}{14} \\ 1 + \frac{27}{14} \end{array}) = (\begin{array}{c} - \frac{23}{14} \\ \frac{10}{14} \\ \frac{41}{14} \end{array})$ $\Rightarrow F (- \frac{23}{14} | \frac{10}{14} | \frac{41}{14})$
3. Berechne den Vektor $\vec{P F}$
$\vec{P F} = \vec{O F} - \vec{O P} = (\begin{array}{c} - \frac{23}{14} \\ \frac{10}{14} \\ \frac{41}{14} \end{array}) - (\begin{array}{c} - 1 \\ 2 \\ 1 \end{array}) = (\begin{array}{c} - \frac{9}{14} \\ - \frac{18}{14} \\ \frac{27}{14} \end{array})$
4. Setze $\vec{O P}$ und $\vec{P F}$ in die Vektorgleichung $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F}$ ein:
$\vec{O P^{'}} = (\begin{array}{c} - 1 \\ 2 \\ 1 \end{array}) + 2 \cdot (\begin{array}{c} - \frac{9}{14} \\ - \frac{18}{14} \\ \frac{27}{14} \end{array}) = (\begin{array}{c} - 1 - \frac{18}{14} \\ 2 - \frac{36}{14} \\ 1 + \frac{54}{14} \end{array}) = (\begin{array}{c} - \frac{32}{14} \\ - \frac{8}{14} \\ \frac{68}{14} \end{array})$
5. Berechne den Vektor $\vec{S P^{'}} :$
$\vec{S P^{'}} = \vec{O P^{'}} - \vec{O S} = (\begin{array}{c} - \frac{32}{14} \\ - \frac{8}{14} \\ \frac{68}{14} \end{array}) - (\begin{array}{c} 11 \\ 5 \\ 10 \end{array}) = (\begin{array}{c} - \frac{32}{14} - 11 \\ - \frac{8}{14} - 5 \\ \frac{68}{14} - 10 \end{array}) = (\begin{array}{c} - \frac{93}{7} \\ - \frac{39}{7} \\ - \frac{36}{7} \end{array})$
6. Die Gleichung der Spiegelgeraden lautet dann:
$g^{'} : \vec{x} = \vec{O S} + t \cdot \vec{S P^{'}}$
$g^{'} : \vec{x} = (\begin{array}{c} 11 \\ 5 \\ 10 \end{array}) + t \cdot (\begin{array}{c} - \frac{93}{7} \\ - \frac{39}{7} \\ - \frac{36}{7} \end{array})$ oder $g^{'} : \vec{x} = (\begin{array}{c} 11 \\ 5 \\ 10 \end{array}) + t \cdot (\begin{array}{c} 31 \\ 13 \\ 12 \end{array})$

Spiegele die Gerade $g$ an der Geraden $h$ .

$g : \vec{x} = (\begin{array}{c} 4 \\ 0 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array})$ und $h : \vec{x} = (\begin{array}{c} 6 \\ 1 \\ 3 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array})$ . Die Gerade $g$ ist (echt) parallel zur Geraden $h$ .

$g : \vec{x} = (\begin{array}{c} 2 \\ 3 \\ 6 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ 5 \end{array})$ und $h : \vec{x} = (\begin{array}{c} 3 \\ 1 \\ 1 \end{array}) + s \cdot (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array})$ . Die Geraden schneiden sich im Punkt $S (1 | 3 | 1)$ .

Die Ebene $E$ soll an der Ebene $H$ gespiegelt werden.

Gegeben sind die beiden (echt) parallelen Ebenen
$E : 2 \cdot x_{1} - 3 x_{2} + x_{3} = 7$ und $H : 2 \cdot x_{1} - 3 x_{2} + x_{3} = 12$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung einer Ebene an einer Ebene
Die Ebene $E$ wird an der Ebene $H$ gespiegelt.
Für die rechte Seite der gespiegelten Ebene $E^{'}$ in Koordinatenform gilt die Gleichung:
$(I) d_{3} = 2 \cdot d_{2} - d_{1}$
Lies $d_{1}$ aus der Ebenengleichung $E$ ab: $d_{1} = 7$
Lies $d_{2}$ aus der Ebenengleichung $H$ ab: $d_{2} = 12$
Setze $d_{1} = 7$ und $d_{2} = 12$ in Gleichung $(I)$ ein:
$d_{3} = 2 \cdot 12 - 7 = 24 - 7 = 17$
Antwort: Die Gleichung der Spiegelebene $E^{'}$ lautet: $2 \cdot x_{1} - 3 x_{2} + x_{3} = 17$

$E : 2 \cdot x_{1} + 4 \cdot x_{2} - 2 \cdot x_{3} = 5$ und $H : 3 \cdot x_{1} - x_{2} + 4 x_{3} = 8$ .

Die Gleichung der Schnittgeraden lautet: $g_{S} : \vec{x} = (\begin{array}{c} \frac{18}{7} \\ 0 \\ \frac{1}{14} \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 1 \end{array})$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung einer Ebene an einer Ebene

1. Die Schnittgerade $g_{S}$ ist gegeben: $g_{S} : \vec{x} = \vec{O A} + r \cdot \vec{u} = (\begin{array}{c} \frac{18}{7} \\ 0 \\ \frac{1}{14} \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 1 \end{array})$ .

2. Finde einen Punkt $P$ auf der Ebene $E$ . Der Punkt $P$ darf nicht auf der Schnittgeraden $g_{S}$ liegen.

$E : 2 \cdot x_{1} + 4 \cdot x_{2} - 2 \cdot x_{3} = 5$

Setze z. B. $x_{1} = 1$ und $x_{2} = 1$ und berechne $x_{3}$ :

$2 \cdot 1 + 4 \cdot 1 - 2 \cdot x_{3} = 5 \Rightarrow x_{3} = 0,5 \Rightarrow P (1 | 1 | 0,5)$

Liegt $P$ auf $g_{S}$ ? Setze $P$ in die Geradengleichung ein:

$(\begin{array}{c} 1 \\ 1 \\ 0,5 \end{array}) = (\begin{array}{c} \frac{18}{7} \\ 0 \\ \frac{1}{14} \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 1 \end{array}) \Rightarrow (\begin{array}{c} - \frac{11}{7} \\ 1 \\ \frac{3}{7} \end{array}) = r \cdot (\begin{array}{c} - 1 \\ 1 \\ 1 \end{array})$

Aus der ersten Zeile folgt $r = \frac{11}{7}$ und aus der zweiten Zeile folgt $r = 1$ . Das ist ein Widerspruch. Somit liegt $P$ nicht auf $g_{S} .$

3. Wird ein Punkt $P$ der Ebene $E$ an der Ebene $H$ gespiegelt, so liegen der Punkt $P$ und der Spiegelpunkt $P^{'}$ auf einer Geraden, die senkrecht auf der Ebene $H$ steht. Diese Gerade ist die Lotgerade $l_{L o t}$ . Sie wird benötigt, um den Lotfußpunkt $F$ auf der Ebene $H$ zu berechnen.

Erstelle nun eine Lotgerade $l_{L o t}$ mit dem gefundenen Punkt $P (1 | 1 | 0,5)$ als Aufpunkt und dem Normalenvektor ${\vec{n}}_{H} = (\begin{array}{c} 3 \\ - 1 \\ 4 \end{array})$ der Ebene $H$ : $l_{L o t} : \vec{x} = (\begin{array}{c} 1 \\ 1 \\ 0,5 \end{array}) + r \cdot (\begin{array}{c} 3 \\ - 1 \\ 4 \end{array})$

4. Schneide die Lotgerade $l_{L o t}$ mit der Ebene $H$ , um den Lotfußpunkt $F$ zu erhalten.

$3 \cdot x_{1} - x_{2} + 4 x_{3}$	$=$	$8$
	↓	Setze die Lotgerade $l_{L o t} : \vec{x} = (\begin{array}{c} 1 \\ 1 \\ 0,5 \end{array}) + r \cdot (\begin{array}{c} 3 \\ - 1 \\ 4 \end{array})$ in $H$ ein.
$3 \cdot (1 + 3 r) - (1 - r) + 4 \cdot (0,5 + 4 r)$	$=$	$8$
	↓	Löse die Klammern auf.
$3 + 9 r - 1 + r + 2 + 16 r$	$=$	$8$
	↓	Fasse zusammen.
$4 + 26 r$	$=$	$8$	$- 4$
	↓	Löse nach $r$ auf.
$26 r$	$=$	$4$	$: 26$
$r$	$=$	$\frac{4}{26}$
	↓	Kürze.
$r$	$=$	$\frac{2}{13}$

Setze $r = \frac{2}{13}$ in die Lotgerade $l_{L o t}$ ein, um den Punkt $F$ zu berechnen.

${\vec{x}}_{F} = (\begin{array}{c} 1 \\ 1 \\ 0,5 \end{array}) + (\frac{2}{13}) \cdot (\begin{array}{c} 3 \\ - 1 \\ 4 \end{array}) = (\begin{array}{c} 1 + \frac{6}{13} \\ 1 - \frac{2}{13} \\ 0,5 + \frac{8}{13} \end{array}) = (\begin{array}{c} \frac{19}{13} \\ \frac{11}{13} \\ \frac{29}{26} \end{array}) \Rightarrow$ $F (\frac{19}{13} | \frac{11}{13} | \frac{29}{26})$

5. Für den Spiegelpunkt $P^{'}$ gilt immer die Gleichung $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F}$

Berechne zunächst den Vektor $\vec{P F}$ :

$\vec{P F} = \vec{O F} - \vec{O P} = (\begin{array}{c} \frac{19}{13} \\ \frac{11}{13} \\ \frac{29}{26} \end{array}) - (\begin{array}{c} 1 \\ 1 \\ 0,5 \end{array}) = (\begin{array}{c} \frac{19}{13} - 1 \\ \frac{11}{13} - 1 \\ \frac{29}{26} - 0,5 \end{array}) = (\begin{array}{c} \frac{6}{13} \\ - \frac{2}{13} \\ \frac{8}{13} \end{array})$

6. Setze dann $\vec{O P}$ und $\vec{P F}$ in die Vektorgleichung $\vec{O P^{'}} = \vec{O P} + 2 \cdot \vec{P F}$ ein:

$\vec{O P^{'}} = (\begin{array}{c} 1 \\ 1 \\ 0,5 \end{array}) + 2 \cdot (\begin{array}{c} \frac{6}{13} \\ - \frac{2}{13} \\ \frac{8}{13} \end{array}) = (\begin{array}{c} 1 + \frac{12}{13} \\ 1 - \frac{4}{13} \\ 0,5 + \frac{16}{13} \end{array}) = (\begin{array}{c} \frac{25}{13} \\ \frac{9}{13} \\ \frac{45}{26} \end{array})$

Der Spiegelpunkt hat die Koordinaten $P^{'} (\frac{25}{13} | \frac{9}{13} | \frac{45}{26})$ .

7. Der berechnete Punkt $P^{'}$ ist ein Punkt der Spiegelebene $E^{'}$ . Erstelle eine Parameterform für die Spiegelebene $E^{'}$ mit der Schnittgeraden $g_{S}$ und einem weiteren Richtungsvektor $\vec{v} = \vec{A P^{'}}$ ( $A$ ist der Aufpunkt der Schnittgeraden)

$\Rightarrow$ $E^{'} : \vec{x} = \vec{O A} + r \cdot \vec{u} + s \cdot \vec{v}$ .

Berechne den zweiten Richtungsvektor:

$\vec{v} = \vec{A P^{'}} = \vec{O P^{'}} - \vec{O A} = (\begin{array}{c} \frac{25}{13} \\ \frac{9}{13} \\ \frac{45}{26} \end{array}) - (\begin{array}{c} \frac{18}{7} \\ 0 \\ \frac{1}{14} \end{array}) = (\begin{array}{c} \frac{25}{13} - \frac{18}{7} \\ \frac{9}{13} - 0 \\ \frac{45}{26} - \frac{1}{14} \end{array}) = (\begin{array}{c} - \frac{59}{91} \\ \frac{9}{13} \\ \frac{151}{91} \end{array}) = \frac{1}{91} \cdot (\begin{array}{c} - 59 \\ 63 \\ 151 \end{array})$

Die Spiegelebene $E^{'}$ kann dann als Parametergleichung geschrieben werden:

$E^{'} : \vec{x} = (\begin{array}{c} \frac{18}{7} \\ 0 \\ \frac{1}{14} \end{array}) + r \cdot (\begin{array}{c} - 1 \\ 1 \\ 1 \end{array}) + s \cdot (\begin{array}{c} - 59 \\ 63 \\ 151 \end{array})$

7
Der Punkt $P (2 | 1 | 3)$ wird an der Ebene $E$ gespiegelt. Der Spiegelpunkt $P^{'}$ hat die Koordinaten $P^{'} (8 | 2 | 5)$ . Bestimme die Gleichung der Spiegelebene $E$ in Koordinatenform.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Ebene spiegeln
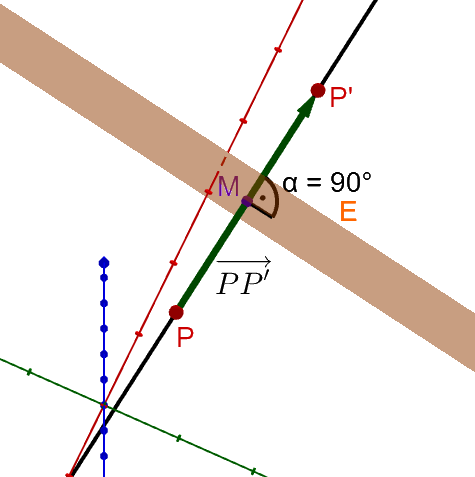
Der Vektor $\vec{P P^{'}} = \vec{O P^{'}} - \vec{O P} = (\begin{array}{c} 8 \\ 2 \\ 5 \end{array}) - (\begin{array}{c} 2 \\ 1 \\ 3 \end{array}) = (\begin{array}{c} 6 \\ 1 \\ 2 \end{array})$ ist der Normalenvektor der Ebene $E$ .
Der Vektor $\vec{O M}$ ist der Vektor, der vom Koordinatenursprung aus zur Mitte des Vektors $\vec{P P^{'}}$ zeigt. Der Punkt $M$ ist ein Punkt in der Ebene $E$ .
Berechne den Vektor $\vec{O M}$ :
$\vec{O M} = \frac{1}{2} \cdot (\vec{O P} + \vec{O P^{'}}) = \frac{1}{2} \cdot ((\begin{array}{c} 2 \\ 1 \\ 3 \end{array}) + (\begin{array}{c} 8 \\ 2 \\ 5 \end{array})) = \frac{1}{2} \cdot (\begin{array}{c} 10 \\ 3 \\ 8 \end{array}) = (\begin{array}{c} 5 \\ 1,5 \\ 4 \end{array})$
Mit dem berechneten Vektor $\vec{O M}$ und dem Normalenvektor $\vec{n} = (\begin{array}{c} 6 \\ 1 \\ 2 \end{array})$ der Ebene $E$ kann die Ebenengleichung in Normalenform folgendermaßen geschrieben werden:
$E : (\vec{x} - (\begin{array}{c} 5 \\ 1,5 \\ 4 \end{array})) \circ (\begin{array}{c} 6 \\ 1 \\ 2 \end{array}) = 0$
Die Ebenengleichung wird in Koordinatenform umgerechnet, indem das Skalarprodukt ausgerechnet wird:
$E : 6 \cdot x_{1} + 1 \cdot x_{2} + 2 \cdot x_{3} - (5 \cdot 6 + 1,5 \cdot 1 + 4 \cdot 2) = 0$
$\Rightarrow E : 6 \cdot x_{1} + x_{2} + 2 \cdot x_{3} - 39,5 = 0$ oder $E : 6 \cdot x_{1} + x_{2} + 2 \cdot x_{3} = 39,5$
Antwort: Die Gleichung der Spiegelebene lautet $E : 6 \cdot x_{1} + x_{2} + 2 \cdot x_{3} = 39,5$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$(\vec{x} - (\begin{array}{c} 4 \\ 0 \\ 1 \end{array})) \circ (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array})$	$=$	$0$
	↓	Setze $h : \vec{x} = (\begin{array}{c} 6 \\ 1 \\ 3 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array})$ ein.
$((\begin{array}{c} 6 \\ 1 \\ 3 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array}) - (\begin{array}{c} 4 \\ 0 \\ 1 \end{array})) \circ (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array})$	$=$	$0$
	↓	Berechne die Vektordifferenz in der Klammer.
$((\begin{array}{c} 2 \\ 1 \\ 2 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array})) \circ (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array})$	$=$	$0$
	↓	Fasse zusammen
$(\begin{array}{c} 2 + 2 s \\ 1 + s \\ 2 - s \end{array}) \circ (\begin{array}{c} 2 \\ 1 \\ - 1 \end{array})$	$=$	$0$
	↓	Berechne das Skalarprodukt.
$(2 + 2 s) \cdot 2 + (1 + s) \cdot 1 + (2 - s) \cdot (- 1)$	$=$	$0$
	↓	Löse die Klammern auf.
$4 + 4 s + 1 + s - 2 + s$	$=$	$0$
	↓	Löse nach $s$ auf.
$6 s + 3$	$=$	$0$	$- 3$
$6 s$	$=$	$- 3$	$: 6$
$s$	$=$	$- \frac{3}{6}$
	↓	Kürze
$s$	$=$	$- \frac{1}{2}$

$0 (\vec{x} - (\begin{array}{c} 1 \\ 2 \\ 5 \end{array})) \circ (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})$	$=$	$0$
	↓	Setze $g : \vec{x} = (\begin{array}{c} 1 \\ 2 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})$ in H ein.
$((\begin{array}{c} 1 \\ 2 \\ 0 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 1 \\ 2 \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 5 \end{array})) \circ (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})$	$=$	$0$
	↓	Berechne die Vektordifferenz in der Klammer.
$((\begin{array}{c} 0 \\ 0 \\ - 5 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})) \circ (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})$	$=$	$0$
	↓	Fasse zusammen.
$(\begin{array}{c} 0 + r \\ 0 + r \\ - 5 + 2 r \end{array}) \circ (\begin{array}{c} 1 \\ 1 \\ 2 \end{array})$	$=$	$0$
	↓	Berechne das Skalarprodukt.
$(0 + r) \cdot 1 + (0 + r) \cdot 1 + (- 5 + 2 r) \cdot 2$	$=$	$0$
	↓	Löse die Klammern auf.
$r + r - 10 + 4 r$	$=$	$0$
	↓	Fasse zusammen.
$6 r - 10$	$=$	$0$	$+ 10$
	↓	Löse nach $r$ auf.
$6 r$	$=$	$10$	$: 6$
$r$	$=$	$\frac{10}{6}$
	↓	Kürze.
$r$	$=$	$\frac{5}{3}$

$(\vec{x} - (\begin{array}{c} 1 \\ 2 \\ 5 \end{array})) \circ (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array})$	$=$	$0$
	↓	Setze $h : \vec{x} = (\begin{array}{c} - 2 \\ 1 \\ 3 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array})$ in H ein.
$((\begin{array}{c} - 2 \\ 1 \\ 3 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 5 \end{array})) \circ (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array})$	$=$	$0$
	↓	Berechne die Vektordifferenz in der Klammer.
$((\begin{array}{c} - 3 \\ - 1 \\ - 2 \end{array}) + r \cdot (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array})) \circ (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array})$	$=$	$0$
	↓	Fasse zusammen.
$(\begin{array}{c} - 3 + r \\ - 1 - 2 r \\ - 2 + 0 r \end{array}) \circ (\begin{array}{c} 1 \\ - 2 \\ 0 \end{array})$	$=$	$0$
	↓	Berechne das Skalarprodukt.
$(- 3 + r) \cdot 1 + (- 1 - 2 r) \cdot (- 2) + (- 2 + 0 r) \cdot 0$	$=$	$0$
	↓	Löse die Klammern auf
$- 3 + r + 2 + 4 r + 0$	$=$	$0$
	↓	Fasse zusammen.
$5 r - 1$	$=$	$0$	$+ 1$
	↓	Löse nach $r$ auf.
$5 r$	$=$	$1$	$: 5$
$r$	$=$	$\frac{1}{5}$

$x_{1} + 3 x_{2} - 2 x_{3}$	$=$	$11$
	↓	Setze $h : \vec{x} = (\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 3 \\ - 2 \end{array})$ in $E$ ein.
$(1 + r) + 3 \cdot (2 + 3 r) - 2 \cdot (5 - 2 r)$	$=$	$11$
	↓	Löse die Klammern auf.
$1 + r + 6 + 9 r - 10 + 4 r$	$=$	$11$
	↓	Fasse zusammen.
$- 3 + 14 r$	$=$	$11$	$+ 3$
	↓	Löse nach r auf.
$14 r$	$=$	$14$	$: 14$
$r$	$=$	$1$

$- 2 x_{1} + x_{2} + 3 x_{3}$	$=$	$43$
	↓	Setze $h : \vec{x} = (\begin{array}{c} 1 \\ 2 \\ 5 \end{array}) + r \cdot (\begin{array}{c} - 2 \\ 1 \\ 3 \end{array})$ in $F$ ein.
$- 2 \cdot (1 - 2 r) + (2 + r) + 3 \cdot (5 + 3 r)$	$=$	$43$
	↓	Löse die Klammern auf.
$- 2 + 4 r + 2 + r + 15 + 9 r$	$=$	$43$
	↓	Fasse zusammen.
$15 + 14 r$	$=$	$43$	$- 15$
	↓	Löse nach r auf.
$14 r$	$=$	$28$	$: 14$
$r$	$=$	$2$

$4 x_{1} - 2 x_{2} + 2 x_{3}$	$=$	$30$
	↓	Setze $l_{L o t} : \vec{x} = (\begin{array}{c} 2 \\ 4 \\ 3 \end{array}) + s \cdot (\begin{array}{c} 4 \\ - 2 \\ 2 \end{array})$ in $E$ ein.
$4 \cdot (2 + 4 s) - 2 \cdot (4 - 2 s) + 2 \cdot (3 + 2 s)$	$=$	$30$
	↓	Löse die Klammern auf.
$8 + 16 s - 8 + 4 s + 6 + 4 s$	$=$	$30$
	↓	Fasse zusammen.
$6 + 24 s$	$=$	$30$	$- 6$
$24 s$	$=$	$24$	$: 24$
$s$	$=$	$1$

$x_{1} + 2 x_{2} - 3 x_{3}$	$=$	$- 9$
	↓	Setze $l_{L o t} : \vec{x} = (\begin{array}{c} - 1 \\ 2 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ - 3 \end{array})$ in $E$ ein.
$(- 1 + s) + 2 \cdot (2 + 2 s) - 3 \cdot (1 - 3 s)$	$=$	$- 9$
	↓	Löse die Klammern auf
$- 1 + s + 4 + 4 s - 3 + 9 s$	$=$	$- 9$
	↓	Fasse zusammen.
$14 s$	$=$	$- 9$	$: 14$
$s$	$=$	$- \frac{9}{14}$

$(\vec{x} - (\begin{array}{c} 2 \\ 3 \\ 6 \end{array})) \circ (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array})$	$=$	$0$
	↓	Setze $h : \vec{x} = (\begin{array}{c} 3 \\ 1 \\ 1 \end{array}) + s \cdot (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array})$ ein.
$((\begin{array}{c} 3 \\ 1 \\ 1 \end{array}) + s \cdot (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array}) - (\begin{array}{c} 2 \\ 3 \\ 6 \end{array})) \circ (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array})$	$=$	$0$
	↓	Berechne die Vektordifferenz in der Klammer.
$((\begin{array}{c} 1 \\ - 2 \\ - 5 \end{array}) + s \cdot (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array})) \circ (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array})$	$=$	$0$
	↓	Fasse zusammen.
$(\begin{array}{c} 1 - s \\ - 2 + s \\ - 5 + 0 s \end{array}) \circ (\begin{array}{c} - 1 \\ 1 \\ 0 \end{array})$	$=$	$0$
	↓	Berechne das Skalarprodukt.
$(1 - s) \cdot (- 1) + (- 2 + s) \cdot 1 + (- 5 + 0 s) \cdot 0$	$=$	$0$
	↓	Löse die Klammern auf.
$- 1 + s - 2 + s + 0$	$=$
	↓	Fasse zusammen.
$2 s - 3$	$=$	$0$	$+ 3$
	↓	Löse nach $s$ auf.
$2 s$	$=$	$3$	$: 2$
$s$	$=$	$1,5$

Aufgaben zur Spiegelung in der analytischen Geometrie

Lösung der Aufgabe mit Hilfsebene H