Spiegelung einer Geraden an einer Ebene

1. Fall: Die Gerade ist (echt) parallel zur Ebene

Gegeben sind die zu der Ebene $E$ (echt) parallele Gerade $g:\overrightarrow{x}=\overrightarrow{OP}+r\cdot \overrightarrow{u}$ und die Ebene

$E:a{x}_1+b{x}_2+c{x}_3=d$. Die Gerade $g$ wird an der Ebene $E$ gespiegelt.

Vorgehensweise

Berechnung der gespiegelten Geraden g' mit einer Lotgeraden $l_{Lot}$

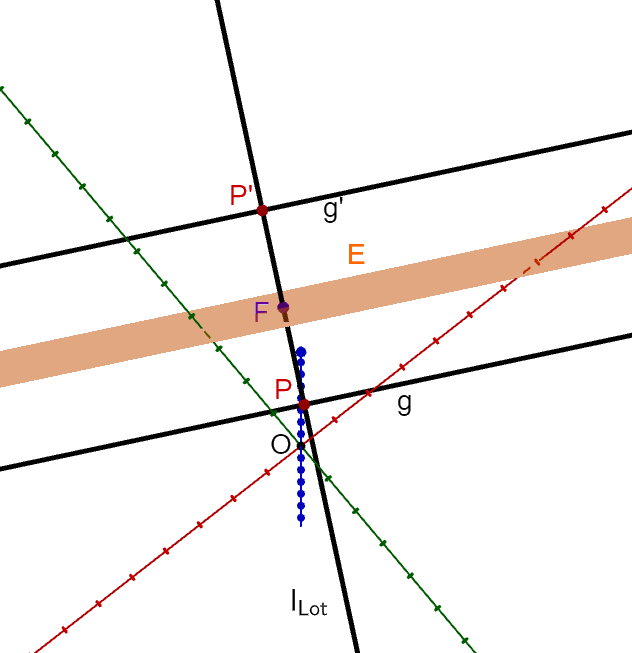
1. Erstelle eine Lotgerade $l_{Lot}$ mit dem Aufpunkt $P$ der Geraden $g$ und mit dem Normalenvektor ${\overrightarrow{n}}_E$ der Ebene $E$: $l_{Lot}:\overrightarrow{x}=\overrightarrow{OP}+s\cdot {\overrightarrow{n}}_E$

2. Schneide die Gerade $l_{Lot}$ mit der Ebene $E$. Du erhältst den Fußpunkt $F$.

3. Berechne den Vektor $\overrightarrow{PF}$

4. Zur Berechnung des Spiegelpunktes $P^{\prime }$ setze $\overrightarrow{OP}$ und $\overrightarrow{PF}$ in die Vektorgleichung $\overrightarrow{O{P}^{\prime }}=\overrightarrow{OP}+2\cdot \overrightarrow{PF}$ ein.

5. Der berechnete Punkt $P^{\prime }$ ist der Aufpunkt der Spiegelgeraden $g^{\prime }$. Die Spiegelgerade hat den Richtungsvektor $\overrightarrow{u}$ (parallele Gerade zu $g$) $\Rightarrow g^{\prime }:\overrightarrow{x}=\overrightarrow{O{P}^{\prime }}+t\cdot \overrightarrow{u}$

Beispiel zu Fall 1

Gegeben sind die zu der Ebene E (echt) parallele Gerade $g:\overrightarrow{x}=\left(\begin{array}{c}1\\ -1\\ 2\end{array}\right)+r\cdot \left(\begin{array}{c}2\\ 1\\ 0\end{array}\right)$und die Ebene $E:2x_1-4x_2+x_3=29$. Die Gerade $g$ wird an der Ebene $E$ gespiegelt.

1. Erstelle die Gleichung einer Lotgeraden $l_{Lot}$ mit dem Aufpunkt $P$ der Geraden $g$ und mit dem Normalenvektor ${\overrightarrow{n}}_E$ der Ebene $E$: $l_{Lot}:\overrightarrow{x}=\overrightarrow{OP}+s\cdot {\overrightarrow{n}}_E=\left(\begin{array}{c}1\\ -1\\ 2\end{array}\right)+s\cdot \left(\begin{array}{c}2\\ -4\\ 1\end{array}\right)$

2. Schneide die Gerade $l_{Lot}$ mit der Ebene $E$.

$l_{Lot}\cap E$

Setze $s=1$ in die Lotgeradengleichung $l_{Lot}$ ein, um den Punkt $F$ zu berechnen.

${\overrightarrow{x}}_F=\left(\begin{array}{c}1\\ -1\\ 2\end{array}\right)+1\cdot \left(\begin{array}{c}2\\ -4\\ 1\end{array}\right)=\left(\begin{array}{c}3\\ -5\\ 3\end{array}\right)$$\Rightarrow F(3|-5|3)$

3. Berechne den Vektor $\overrightarrow{PF}$

$\overrightarrow{PF}=\overrightarrow{OF}-\overrightarrow{OP}=\left(\begin{array}{c}3\\ -5\\ 3\end{array}\right)-\left(\begin{array}{c}1\\ -1\\ 2\end{array}\right)=\left(\begin{array}{c}2\\ -4\\ 1\end{array}\right)$

4. Setze $\overrightarrow{OP}$ und $\overrightarrow{PF}$ in die Vektorgleichung $\overrightarrow{O{P}^{\prime }}=\overrightarrow{OP}+2\cdot \overrightarrow{PF}$ ein:

$\overrightarrow{O{P}^{\prime }}=\left(\begin{array}{c}1\\ -1\\ 2\end{array}\right)+2\cdot \left(\begin{array}{c}2\\ -4\\ 1\end{array}\right)=\left(\begin{array}{c}5\\ -9\\ 4\end{array}\right)$

5. Der berechnete Punkt $P^{\prime }$ ist der Aufpunkt der Spiegelgeraden $g^{\prime }$. Die Spiegelgerade hat den Richtungsvektor $\overrightarrow{u}$ (parallele Gerade zu $g$) $\Rightarrow g^{\prime }:\overrightarrow{x}=\overrightarrow{O{P}^{\prime }}+t\cdot \overrightarrow{u}$

Antwort: Die gespiegelte Gerade hat die Gleichung $g^{\prime }:\overrightarrow{x}=\left(\begin{array}{c}5\\ -9\\ 4\end{array}\right)+t\cdot \left(\begin{array}{c}2\\ 1\\ 0\end{array}\right)$

Anmerkung: Die obige Abbildung zeigt das Beispiel zu Fall 1.

2. Fall: Die Gerade schneidet die Ebene in einem Punkt $S$

Gegeben sind die Gerade $g:\overrightarrow{x}=\overrightarrow{OP}+r\cdot \overrightarrow{u}$, die Ebene $E:a{x}_1+b{x}_2+c{x}_3=d$ und der Schnittpunkt $S$ der Geraden mit der Ebene. Die Gerade $g$ wird an der Ebene $E$ gespiegelt.

Vorgehensweise

Berechnung der gespiegelten Geraden g' mit einer Lotgeraden $l_{Lot}$

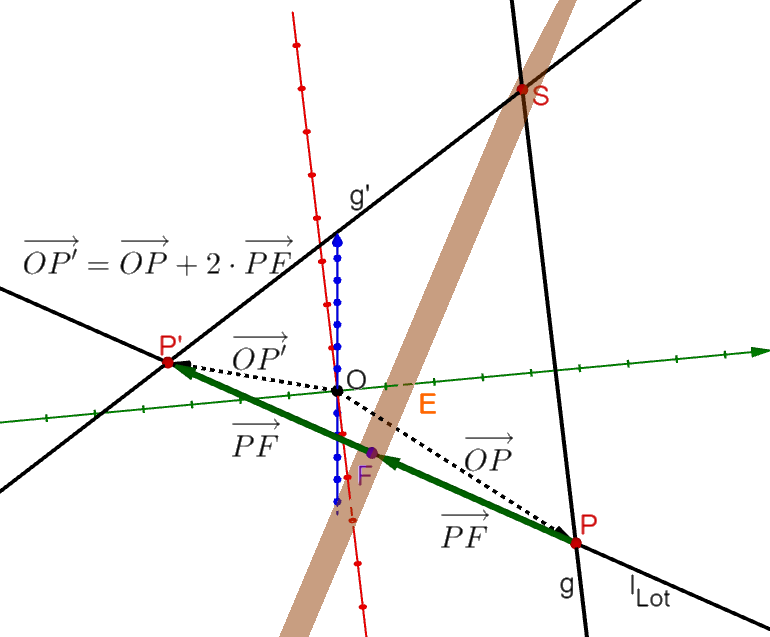
1. Erstelle eine Lotgerade $l_{Lot}$ mit dem Aufpunkt $P$ der Geraden $g$ und mit dem Normalenvektor ${\overrightarrow{n}}_E$ der Ebene $E$: $l_{Lot}:\overrightarrow{x}=\overrightarrow{OP}+s\cdot {\overrightarrow{n}}_E$

2. Schneide die Gerade $l_{Lot}$ mit der Ebene $E$. Du erhältst den Fußpunkt $F$.

3. Berechne den Vektor $\overrightarrow{PF}$

4. Zur Berechnung des Spiegelpunktes $P^{\prime }$ setze $\overrightarrow{OP}$ und $\overrightarrow{PF}$ in die Vektorgleichung $\overrightarrow{O{P}^{\prime }}=\overrightarrow{OP}+2\cdot \overrightarrow{PF}$ ein.

5. Berechne den Vektor $\overrightarrow{S{P}^{\prime }}$ : $\overrightarrow{S{P}^{\prime }}=\overrightarrow{O{P}^{\prime }}-\overrightarrow{OS}$

6. Die Gleichung der Spiegelgeraden lautet dann: $g^{\prime }:\overrightarrow{x}=\overrightarrow{O{P}^{\prime }}+t\cdot \overrightarrow{S{P}^{\prime }}$ oder

$g^{\prime }:\overrightarrow{x}=\overrightarrow{OS}+t\cdot \overrightarrow{S{P}^{\prime }}$

Beispiel zu Fall 2

Gegeben sind die Gerade $g:\overrightarrow{x}=\left(\begin{array}{c}8\\ 9\\ 0\end{array}\right)+r\cdot \left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)$, die Ebene $E:2x_1+4x_2-x_3=10$ und der Schnittpunkt $S(-13|9|0)$ der Geraden mit der Ebene. Die Gerade $g$ wird an der Ebene $E$ gespiegelt.

1. Erstelle die Gleichung einer Lotgeraden $l_{Lot}$ mit dem Aufpunkt $P$ der Geraden $g$ und mit dem Normalenvektor ${\overrightarrow{n}}_E$ der Ebene $E$: $l_{Lot}:\overrightarrow{x}=\overrightarrow{OP}+s\cdot {\overrightarrow{n}}_E=\left(\begin{array}{c}8\\ 9\\ 0\end{array}\right)+s\cdot \left(\begin{array}{c}2\\ 4\\ -1\end{array}\right)$

2. Schneide die Gerade $l_{Lot}$ mit der Ebene $E$.

$l_{Lot}\cap E$

Setze $s=-2$ in die Lotgeradengleichung $l_{Lot}$ ein, um den Punkt $F$ zu berechnen.

${\overrightarrow{x}}_F=\left(\begin{array}{c}8\\ 9\\ 0\end{array}\right)+(-2)\cdot \left(\begin{array}{c}2\\ 4\\ -1\end{array}\right)=\left(\begin{array}{c}8-4\\ 9-8\\ 0+2\end{array}\right)=\left(\begin{array}{c}4\\ 1\\ 2\end{array}\right)$$\Rightarrow F(4|1|2)$

3. Berechne den Vektor $\overrightarrow{PF}$

$\overrightarrow{PF}=\overrightarrow{OF}-\overrightarrow{OP}=\left(\begin{array}{c}4\\ 1\\ 2\end{array}\right)-\left(\begin{array}{c}8\\ 9\\ 0\end{array}\right)=\left(\begin{array}{c}-4\\ -8\\ 2\end{array}\right)$

4. Setze $\overrightarrow{OP}$ und $\overrightarrow{PF}$ in die Vektorgleichung $\overrightarrow{O{P}^{\prime }}=\overrightarrow{OP}+2\cdot \overrightarrow{PF}$ ein:

$\overrightarrow{O{P}^{\prime }}=\left(\begin{array}{c}8\\ 9\\ 0\end{array}\right)+2\cdot \left(\begin{array}{c}-4\\ -8\\ 2\end{array}\right)=\left(\begin{array}{c}8-8\\ 9-16\\ 0+4\end{array}\right)=\left(\begin{array}{c}0\\ -7\\ 4\end{array}\right)$

5. Berechne den Vektor $\overrightarrow{S{P}^{\prime }}:$

$\overrightarrow{S{P}^{\prime }}=\overrightarrow{O{P}^{\prime }}-\overrightarrow{OS}=\left(\begin{array}{c}0\\ -7\\ 4\end{array}\right)-\left(\begin{array}{c}-13\\ 9\\ 0\end{array}\right)=\left(\begin{array}{c}13\\ -16\\ 4\end{array}\right)$

6. Die Gleichung der Spiegelgeraden lautet dann:

$g^{\prime }:\overrightarrow{x}=\overrightarrow{O{P}^{\prime }}+t\cdot \overrightarrow{S{P}^{\prime }}$ oder $g^{\prime }:\overrightarrow{x}=\overrightarrow{OS}+t\cdot \overrightarrow{S{P}^{\prime }}$

Antwort: Die gespiegelte Gerade hat die Gleichung:

$g^{\prime }:\overrightarrow{x}=\left(\begin{array}{c}0\\ -7\\ 4\end{array}\right)+t\cdot \left(\begin{array}{c}13\\ -16\\ 4\end{array}\right)$ oder $g^{\prime }:\overrightarrow{x}=\left(\begin{array}{c}-13\\ 9\\ 0\end{array}\right)+t\cdot \left(\begin{array}{c}13\\ -16\\ 4\end{array}\right)$

Anmerkung: Die obige Abbildung zeigt das Beispiel zu Fall 2.