Punkt an Ebene spiegeln

Die einfachste Vorgehensweise, einen Punkt an einer Ebene zu spiegeln, ist wie folgt:

Hilfsgerade $h$ aufstellen, die senkrecht zur Ebene $E$ steht und durch den Punkt $P$ verläuft.
Schnittpunkt $S$ der Gerade $h$ mit der Ebene $E$ bestimmen.
Vektor $\vec{P S}$ berechnen.
Vektor $\vec{P S}$ zu $\vec{O S}$ addieren, um den gesuchten Punkt $P^{'}$ zu bekommen.

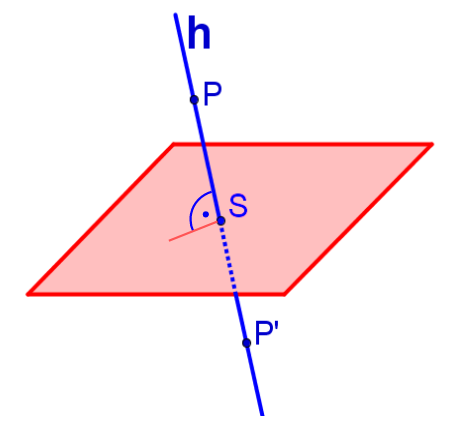
Beispiel

Gegeben: $E : 2 x_{1} + x_{2} + 2 x_{3} = 20$ und $P (7 | 6 | 9)$

Hilfsgerade $h$ bestimmen: Diese soll senkrecht auf der Ebene $E$ stehen; also ist ihr Richtungsvektor der Normalenvektor der Ebene. $\vec{n_{E}} = (\begin{array}{c} 2 \\ 1 \\ 2 \end{array})$ Außerdem soll sie durch $P$ gehen; als Aufpunkt kann man $P$ verwenden, als Stützvektor also $\vec{O P}$ . $\Rightarrow h : \vec{x} = (\begin{array}{c} 7 \\ 6 \\ 9 \end{array}) + λ \cdot (\begin{array}{c} 2 \\ 1 \\ 2 \end{array})$
Schnittpunkt $S$ von der Geraden $h$ mit der Ebene $E$ bestimmen: Dazu wird die Gerade (genauer: der "allgemeine Geradenpunkt") in die Ebenengleichung eingesetzt.
$2 \cdot (7 + 2 λ) + (6 + λ) + 2 \cdot (9 + 2 λ) = 20$
$14 + 4 λ + 6 + λ + 18 + 4 λ = 20$
$38 + 9 λ = 20$
$9 λ = - 18$
$λ = - 2$

Dieser Wert wird nun in die Geradengleichung eingesetzt, um $S$ zu erhalten. $\vec{O S} = (\begin{array}{c} 7 \\ 6 \\ 9 \end{array}) - 2 \cdot (\begin{array}{c} 2 \\ 1 \\ 2 \end{array}) = (\begin{array}{c} 3 \\ 4 \\ 5 \end{array})$ also ist $S (3 | 4 | 5)$ .

Vektor $\vec{P S}$ berechnen: $\vec{P S} = \vec{O S} - \vec{O P} = (\begin{array}{c} 3 \\ 4 \\ 5 \end{array}) - (\begin{array}{c} 7 \\ 6 \\ 9 \end{array}) = (\begin{array}{c} - 4 \\ - 2 \\ - 4 \end{array})$
Spiegelpunkt P' berechnen: $\vec{O P^{'}} = \vec{O S} + \vec{P S} = (\begin{array}{c} 3 \\ 4 \\ 5 \end{array}) + (\begin{array}{c} - 4 \\ - 2 \\ - 4 \end{array}) = (\begin{array}{c} - 1 \\ 2 \\ 1 \end{array})$ , also $P^{'} (- 1 | 2 | 1)$ .

Alternative Berechnung der Spiegelung eines Punktes $P$ an einer Ebene $E$

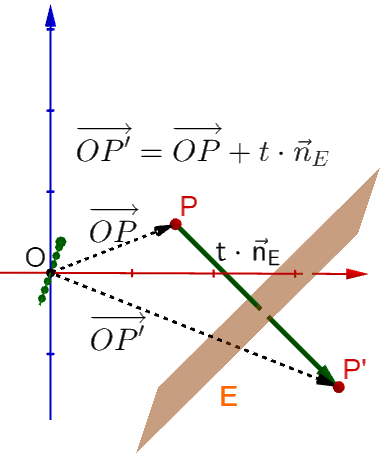
Spiegelung eines Punktes P an der Ebene E

Die Ebene ist durch $\vec{x} \circ \vec{n} = d$ gegeben.

Setze den gegebenen Punkt $P$ in die Ebenengleichung $E$ ein und berechne die Zahl $d_{1}$ :

$\Rightarrow (I) \vec{p} \circ \vec{n} = d_{1}$

Der Spiegelpunkt $P^{'}$ liegt dann in der Ebene $\vec{x} \circ \vec{n} = 2 \cdot d - d_{1}$ (siehe Spiegelung Ebene an Ebene)

$\Rightarrow (I I) \vec{p}^{'} \circ \vec{n} = 2 \cdot d - d_{1}$

Die Verbindung der Punkte $P$ und $P^{'}$ steht senkrecht auf der Ebene $E$ .

Damit ist $(I I I) \vec{p}^{'} = \vec{p} + t \cdot \vec{n}$ .

Zur Berechnung des Spiegelpunktes muss der Parameter $t$ berechnet werden:

Setze $(I I I)$ in $(I I)$ ein:

$\vec{p}^{'} \circ \vec{n}$	$=$	$2 \cdot d - d_{1}$
	↓	Setze $\vec{p}^{'} = \vec{p} + t \cdot \vec{n}$ ein.
$(\vec{p} + t \cdot \vec{n}) \circ \vec{n}$	$=$	$2 \cdot d - d_{1}$
	↓	Löse die Klammer auf.
$\vec{p} \circ \vec{n} + t \cdot \vec{n} \circ \vec{n}$	$=$	$2 \cdot d - d_{1}$

Die Gleichung $(I V)$ lautet nun: $\vec{p} \circ \vec{n} + t \cdot \vec{n} \circ \vec{n} = 2 \cdot d - d_{1}$

Setze $(I)$ in $(I V)$ ein:

$\vec{p} \circ \vec{n} + t \cdot \vec{n} \circ \vec{n}$	$=$	$2 \cdot d - d_{1}$
	↓	Setze $\vec{p} \circ \vec{n} = d_{1}$ ein.
$d_{1} + t \cdot \vec{n} \circ \vec{n}$	$=$	$2 \cdot d - d_{1}$	$- d_{1}$
$t \cdot \vec{n} \circ \vec{n}$	$=$	$2 \cdot d - 2 \cdot d_{1}$
	↓	Klammere auf der rechten Seite $2$ aus.
$t \cdot \vec{n} \circ \vec{n}$	$=$	$2 \cdot (d - d_{1})$	$: \vec{n} \circ \vec{n}$
$t$	$=$	$\frac{2 \cdot (d - d_{1})}{\vec{n} \circ \vec{n}}$

Mit diesem Parameter $t$ wird der Spiegelpunkt $P^{'}$ berechnet:

\vec{p}^{'} = \vec{p} + t \cdot \vec{n} ﻿

Beispiel

Gegeben sind der Punkt $P (3 | 2 | 1)$ und die Ebene $E : \vec{x} \circ (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) = 6$ . Spiegele den Punkt $P$ an der Ebene $E$ .

Die Ebenengleichung $E$ liefert den Normalenvektor $\vec{n} = (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array})$ und $d = 6$ .

1. Setze den gegebenen Punkt $P (3 | 2 | 1)$ in die Ebenengleichung $E : \vec{x} \circ (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) = 6$ ein und berechne die Zahl $d_{1}$ :

$(\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) \circ (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) = d_{1} \Rightarrow d_{1} = 3 \cdot 1 + 2 \cdot 0 + 1 \cdot (- 1) = 3 + 0 - 1 = 2$

2. Berechne $\vec{n} \circ \vec{n}$ :

$(\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) \circ (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) = 1 \cdot 1 + 0 \cdot 0 + (- 1) \cdot (- 1) = 1 + 0 + 1 = 2$

3. Berechne den Parameter $t$ mit $d = 6$ , $d_{1} = 2$ und $\vec{n} \circ \vec{n} = 2$ :

$t = \frac{2 \cdot (d - d_{1})}{\vec{n} \circ \vec{n}} = \frac{2 \cdot (6 - 2)}{2} = 4$

4. Berechne $\vec{p}^{'}$ :

$\vec{p}^{'} = \vec{p} + t \cdot \vec{n} = (\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) + 4 \cdot (\begin{array}{c} 1 \\ 0 \\ - 1 \end{array}) = (\begin{array}{c} 3 + 4 \\ 2 + 0 \\ 1 - 4 \end{array}) = (\begin{array}{c} 7 \\ 2 \\ - 3 \end{array})$