Aufgaben zur Flächenberechnung
Mit diesen Aufgaben kannst du üben, Flächen zu berechnen, die sich aus Punkten in einem Koordinatensystem ergeben.
- 1
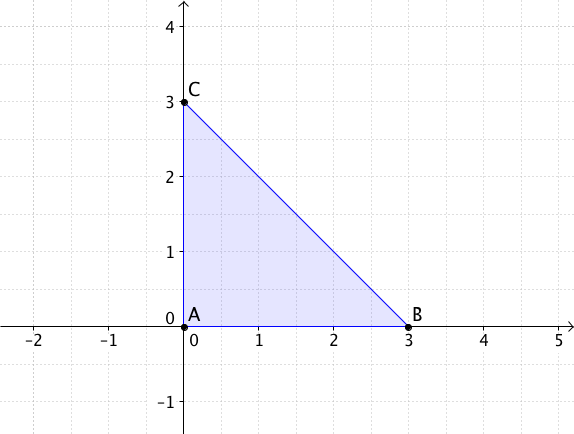
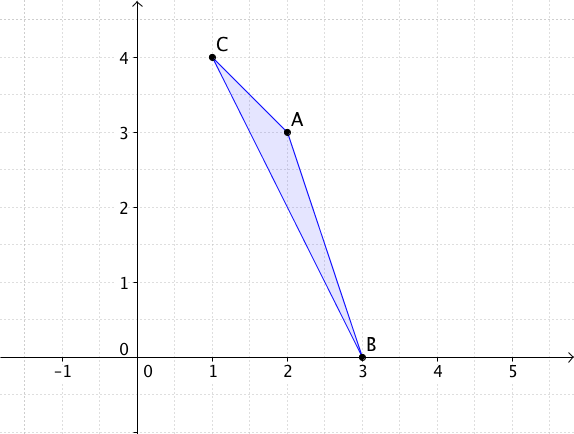
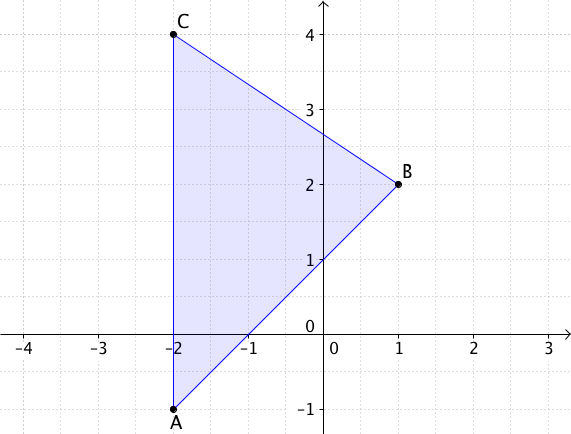
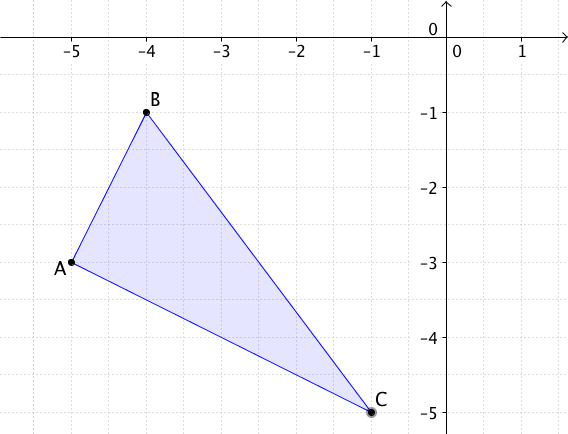
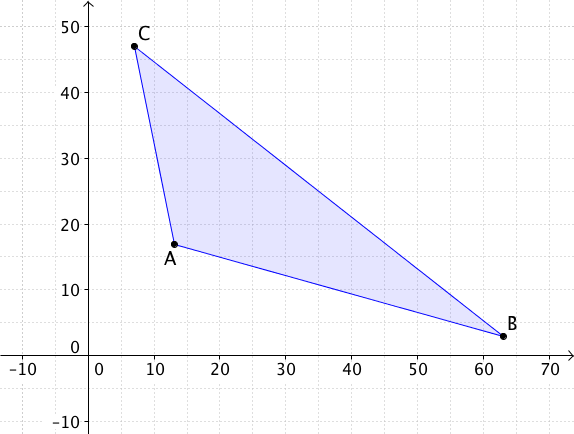
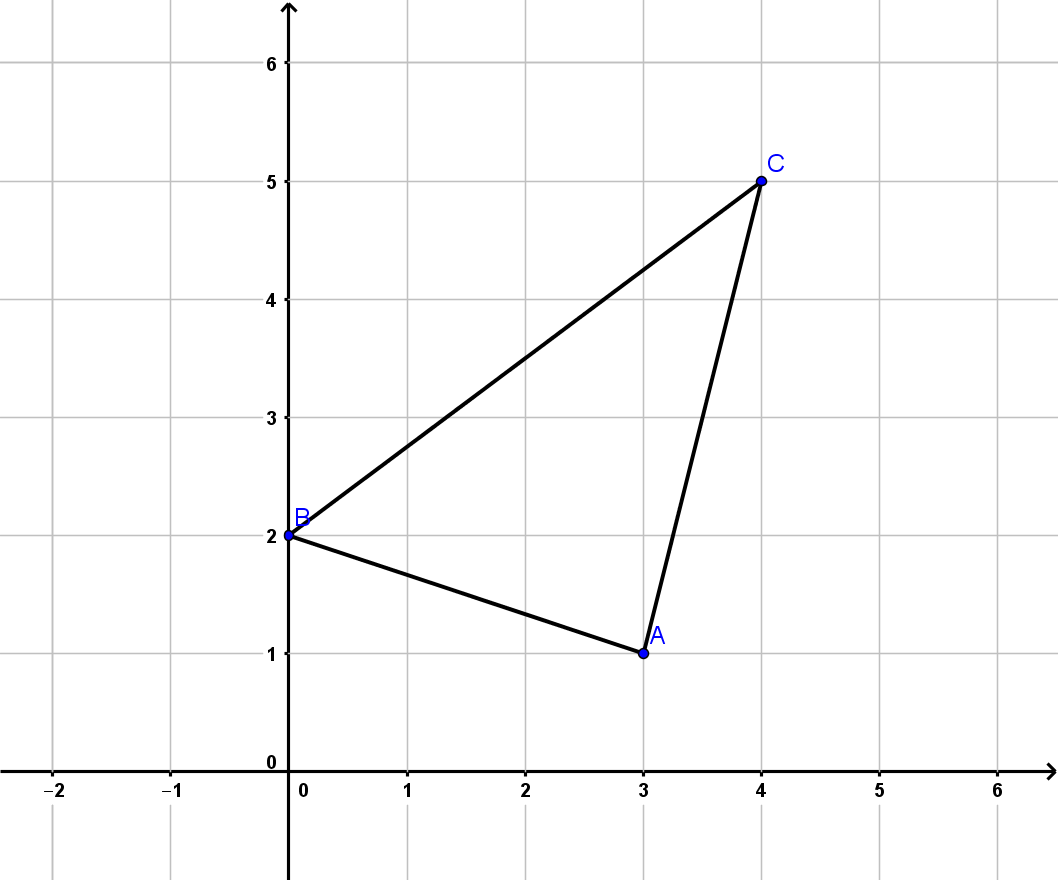
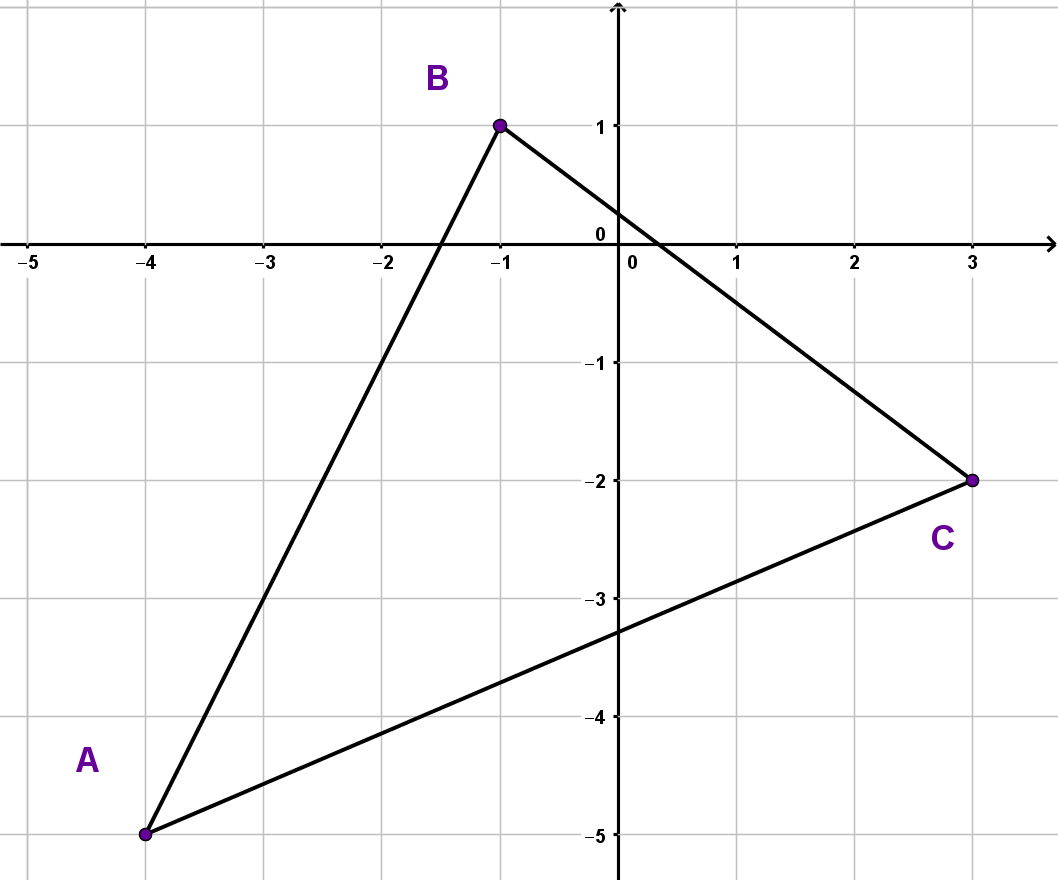
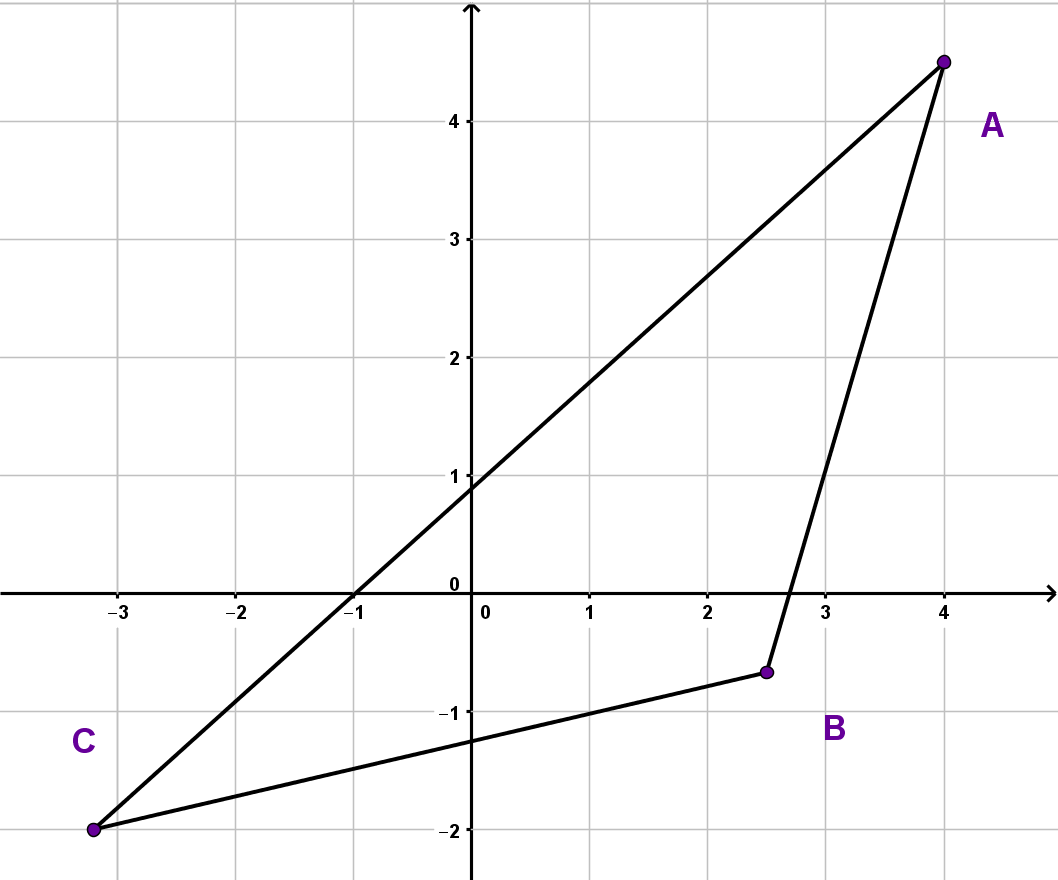
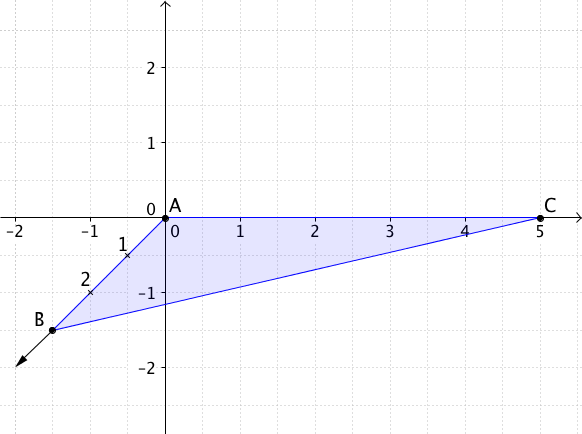
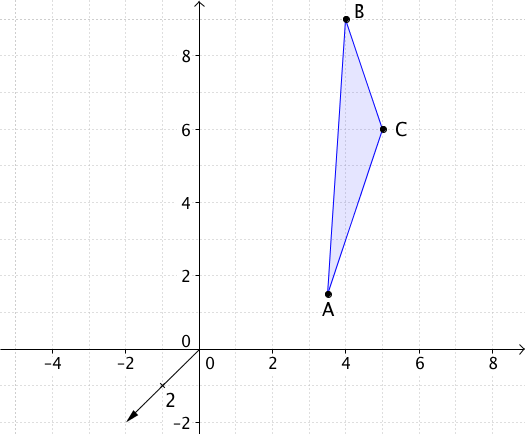
Berechne den Flächeninhalt des Dreiecks, das
durch die Punkte , , gegeben ist.
FEdurch die Punkte , , gegeben ist.
FEdurch die Punkte , , gegeben ist.
FEdurch die Punkte , , gegeben ist.
FEdurch die Punkte , , gegeben ist.
FE
- 2
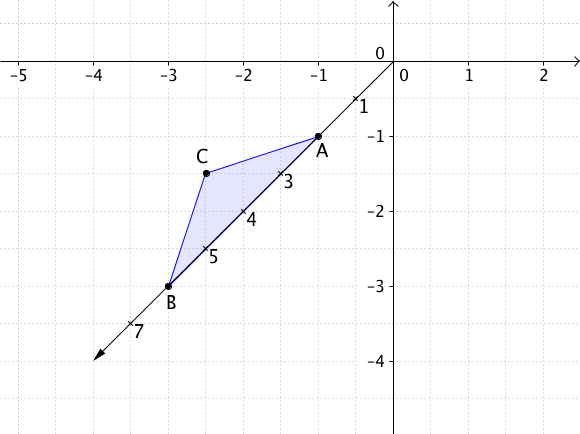
Bestimme den Flächeninhalt des Dreiecks mithilfe der Determinante
, und
FE, und
FE, und
FE
- 3
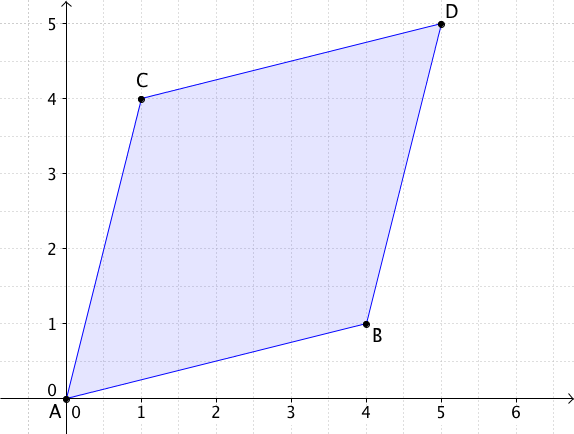
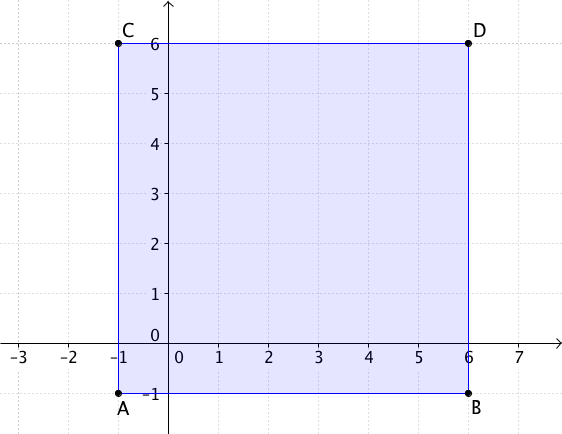
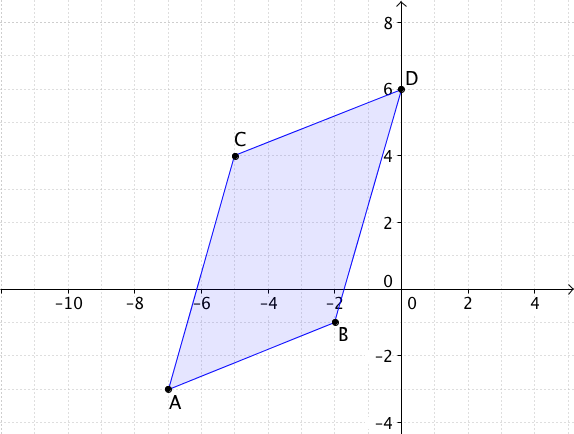
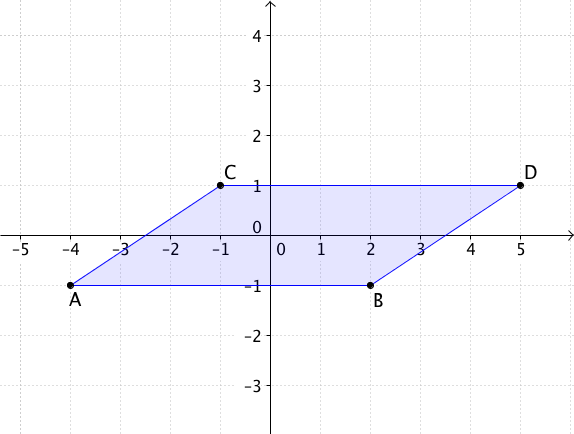
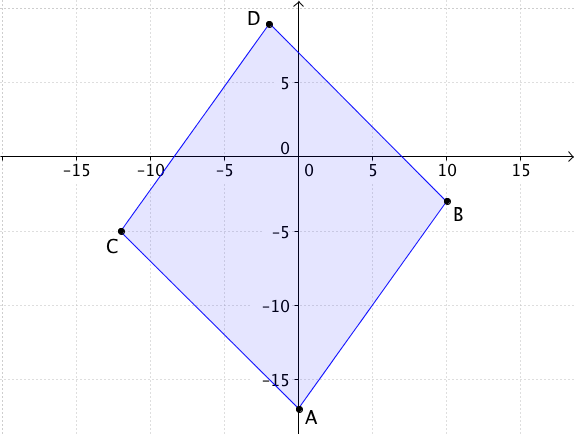
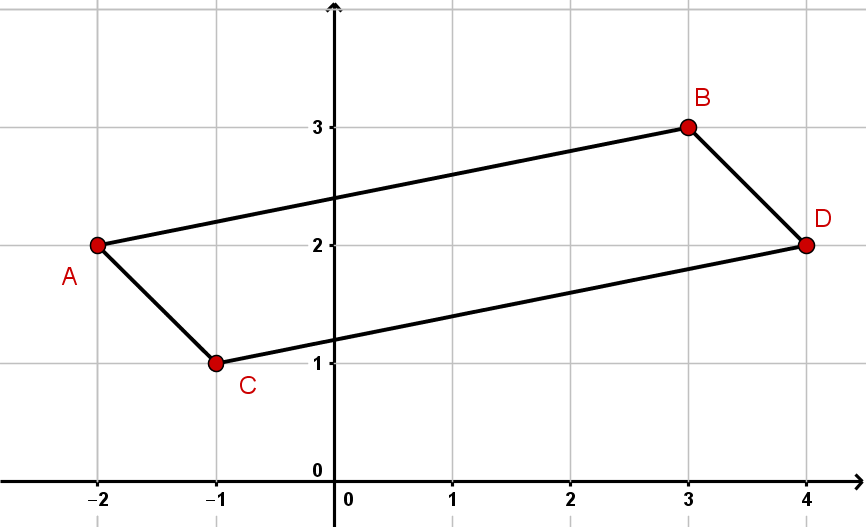
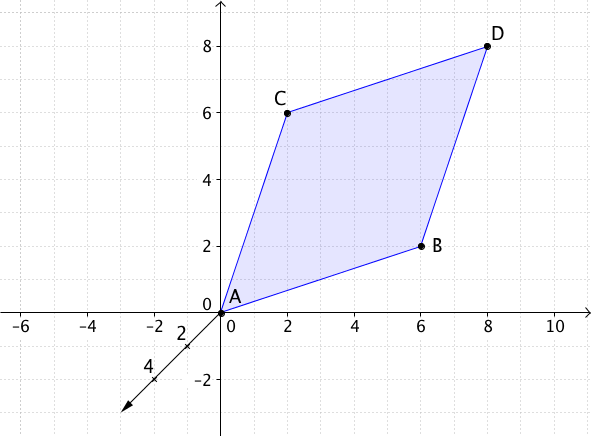
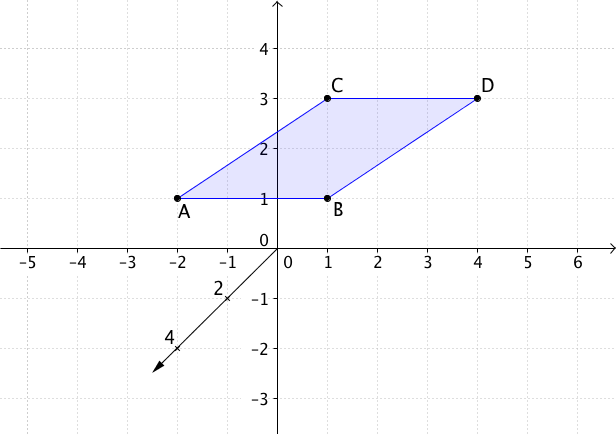
Berechne den Flächeninhalt des Parallelogramms, das
durch die Punkte , , , gegeben ist.
FEdurch die Punkte , , , gegeben ist.
FEdurch die Punkte , , , gegeben ist.
FEdurch die Punkte , , , gegeben ist.
FEdurch die Punkte , , , gegeben ist.
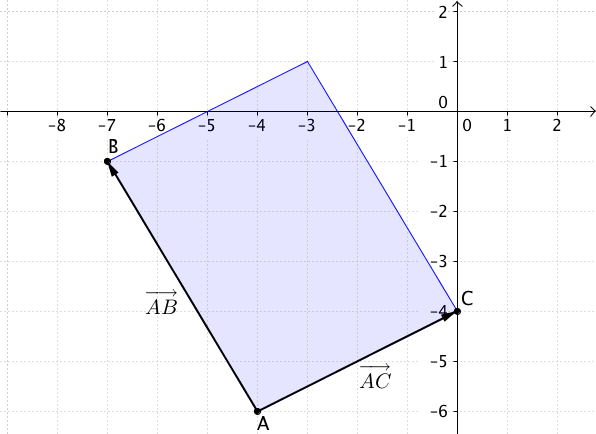
FEden Punkt und die Vektoren und aufgespannt wird.
FEden Punkt und die Vektoren und aufgespannt wird.
FE
- 4
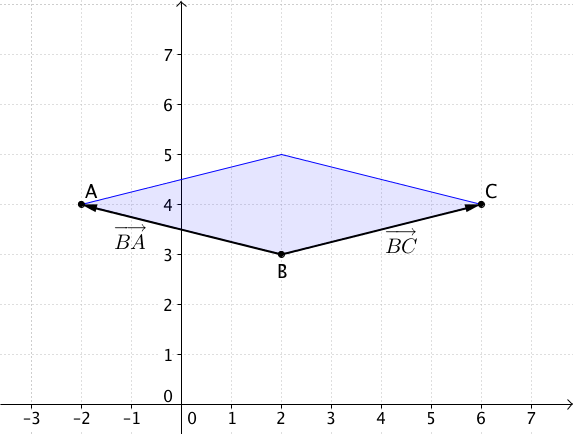
Bestimme den Flächeninhalt des Parallelogramms
und
FEund
FE
- 5
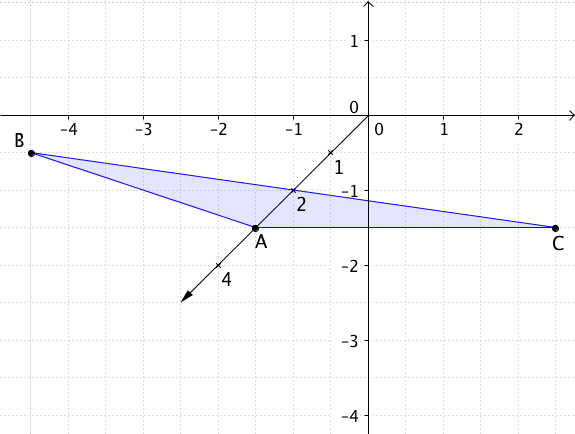
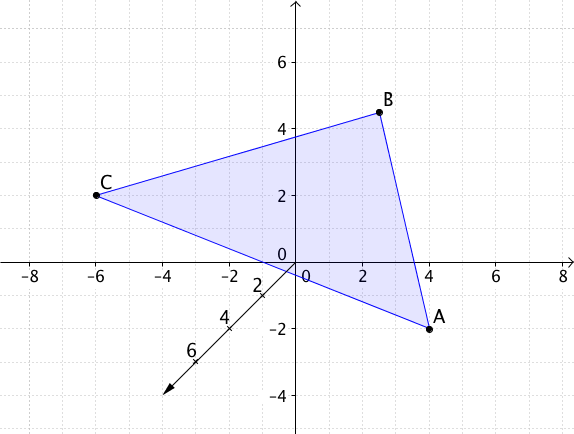
Berechne den Flächeninhalt des Dreiecks, das
durch die Punkte , , gegeben ist.
FEdurch die Punkte , , gegeben ist.
FEdurch die Punkte , , gegeben ist.
FEdurch die Punkte , , gegeben ist.
durch die Punkte , , gegeben ist.
- 6
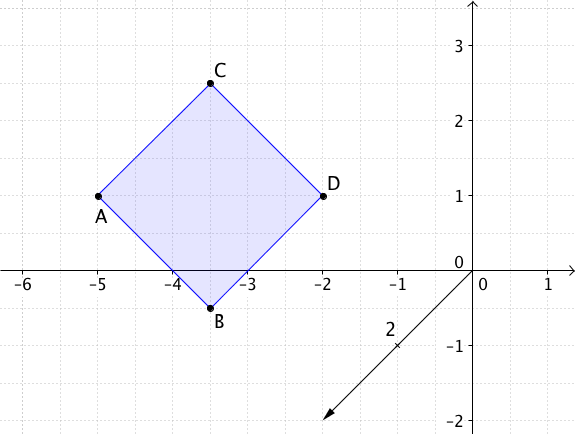
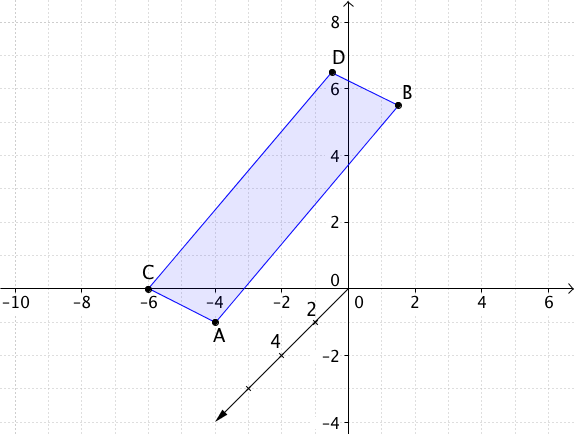
Berechne den Flächeninhalt des Parallelogramms, das durch folgende Punkte gegeben ist. Runde das Ergebnis wenn nötig bis auf zwei Nachkommastellen.
durch die Punkte , , , gegeben ist.
FEdurch die Punkte , , , gegeben ist.
FEdurch die Punkte , , , gegeben ist.
FEdurch die Punkte , , , gegeben ist.
FE
- 7
Berechne den Flächeninhalt des Dreiecks mit , und in Abhängigkeit von .
- 8
Die Punkte sind gegeben durch und , bewegt sich dabei auf der Funktion in Abhängigkeit von .
Bestimme zuerst den Definitionsbereich von und dann den Flächeninhalt des Dreiecks .
- 9
Berechne den Flächeninhalt des Dreiecks , wobei und Punkte sind und der Punkt sich auf der Funktion in Abhängigkeit von bewegt.
- 10
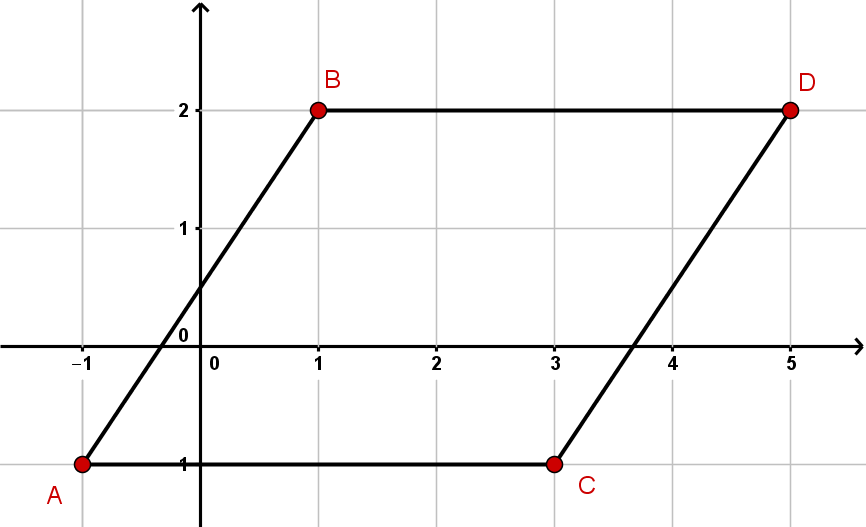
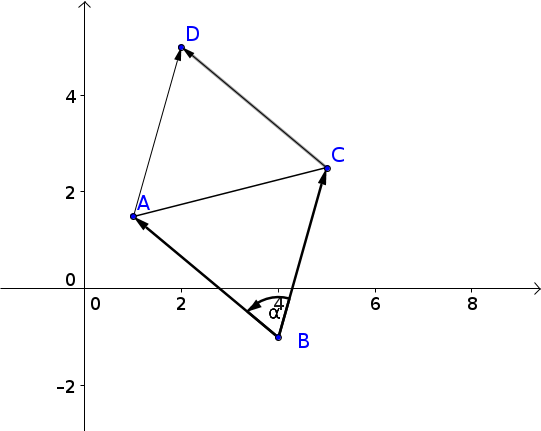
Berechne die Fläche des Parallelogramms, das von den angegebenen Punkten aufgespannt wird.
- FE