Pflichtteil

🎓 Prüfungsbereich für Niedersachsen

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Wichtig: Für die Aufgaben hier gelten andere Nutzungbedingungen.

Aufgaben zur Abiturprüfung eA 2021, Pflichtteil. Zum Download hier.

Aufgabe P1

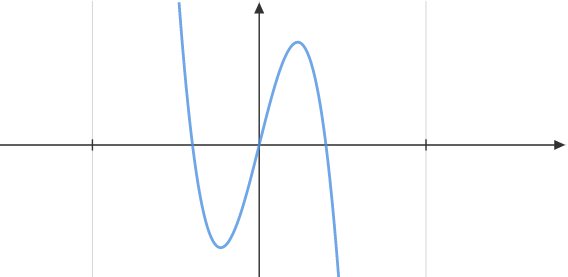
Gegeben ist eine in $ℝ$ definierte Funktion $f$ mit

$f (x) = x^{4} - k \cdot x^{2}$ , wobei $k$ eine positive reelle Zahl ist.

Die Abbildung zeigt den Graphen von $f$ .

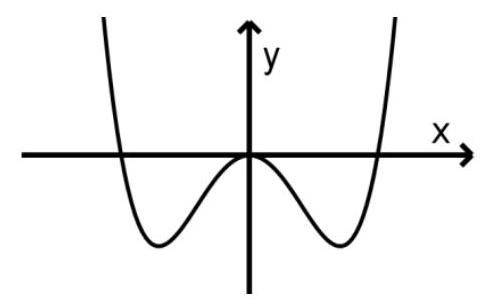
Zeigen Sie, dass $f^{'} (x) = 2 x \cdot (2 x^{2} - k)$ eine Gleichung der ersten Ableitungsfunktion ist. (1 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung von Funktionen
Ableitung mit der Regel für Potenzfunktionen:
$f (x)$ $=$ $x^{4} - k \cdot x^{2}$
↓
Exponent kommt herunter, neuer Exponent wird um $1$ kleiner.
$f^{'} (x)$ $=$ $4 \cdot x^{3} - k \cdot 2 \cdot x^{1}$
↓
$x^{1} = x$
$=$ $4 x^{3} - 2 k x$
↓
Ausklammern von $2 x$
$=$ $2 x \cdot (2 x^{2} - k)$
Damit ist die Ableitung $f^{'} (x) = 2 x \cdot (2 x^{2} - k)$ gezeigt.
Bestimme die Ableitung $f^{'} (x)$ .
Achte darauf, dass $f (x)$ aus Potenzfunktionen besteht.
Klammere den Faktor $2 x$ aus, um den Term zusammenzufassen.

Die beiden Tiefpunkte des Graphen von $f$ haben jeweils die $y$ -Koordinate $- 1$ . Ermitteln Sie den Wert von $k$ . (4 BE)

Aufgabe P2

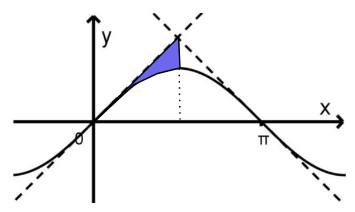
Gegeben ist die in $ℝ$ definierte Funktion $f$ mit $f (x) = \sin (x)$ . Die Abbildung zeigt den Graphen von $f$ sowie die Tangenten an den Graphen in den dargestellten Schnittpunkten mit der $x$ -Achse.

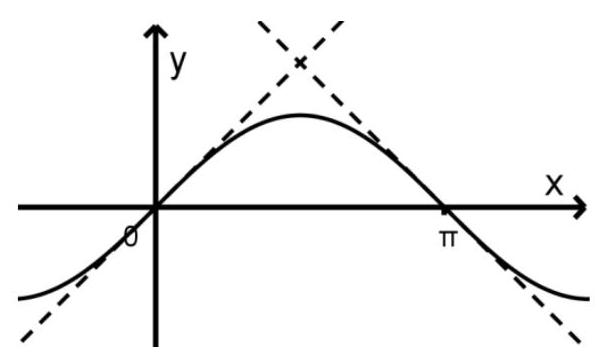
Zeigen Sie, dass diejenige der beiden Tangenten, die durch den Koordinatenursprung verläuft, die Steigung 1 hat. (1 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente und Normale
Die Steigung der Tangente ist gleich der Steigung der Funktion.
Diese ist gegeben durch $f^{'} (0) :$
$f (x)$ $=$ $\sin (x)$
↓
Ableitung von Sinus
$f^{'} (x)$ $=$ $\cos (x)$
$f^{'} (0)$ $=$ $\cos (0)$
$=$ $1$
Die Tangente, die die Funktion an der Stelle $x = 0$ berührt, hat die Steigung $1$ .
Bestimme die Ableitung der Funktion.
Berechne den Wert der Steigung an der Stelle $x = 0$ .

Berechnen Sie den Inhalt des Flächenstücks, das vom Graphen von $f$ und den beiden Tangenten eingeschlossen wird. (4 BE)

Aufgabe P3

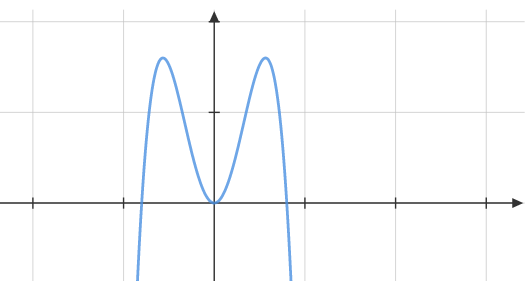
Gegeben sind die in $ℝ$ definierten Funktionen $f$ und $g$ . Der Graph von $f$ ist symmetrisch bezüglich der $y$ -Achse, der Graph von $g$ ist symmetrisch bezüglich des

Koordinatenursprungs. Beide Graphen haben einen Hochpunkt im Punkt $(2 | 1)$ .

Geben Sie für die Graphen von $f$ und $g$ jeweils die Koordinaten und die Art eines weiteren Extrempunktes an. (2 BE)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
Extrempunkt von $f$
Bei einem y-Achsen-symmetrischen Graphen spiegeln sich die Punkte an der y-Achse.
$P (2 | 1) \mapsto P^{'} (- 2 | 1)$
Der Punkt ist ebenfalls ein Hochpunkt.
Skizze als Hilfe. Das ist nicht der Graph von $f$ .
Extrempunkt von $g$
Bei einem punktsymmetrischen Graphen wie hier, spiegeln sich die
Punkte am Ursprung.
$P (2 | 1) \mapsto P^{'} (- 2 | - 1)$
Der Punkt ist ein Tiefpunkt.
Skizze als Hilfe. Das ist nicht der Graph von $g$ .
Bestimme die Koordinaten des zweiten Extrempunktes von $f$ .
Spiegle dazu den Punkt an der y-Achse.
Gib an, ob es sich um einen Hoch- oder Tiefpunkt handelt.
Bestimme die Koordinaten des zweiten Extrempunktes von $g$ .
Spiegle dazu den Punkt am Ursprung.
Gib an, ob es sich um einen Hoch- oder Tiefpunkt handelt.

Untersuchen Sie die in $ℝ$ definierte Funktion $h$ mit $h (x) = f (x) \cdot (g (x))^{3}$ im Hinblick auf eine mögliche Symmetrie ihres Graphen. (3 BE)

4
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe P4
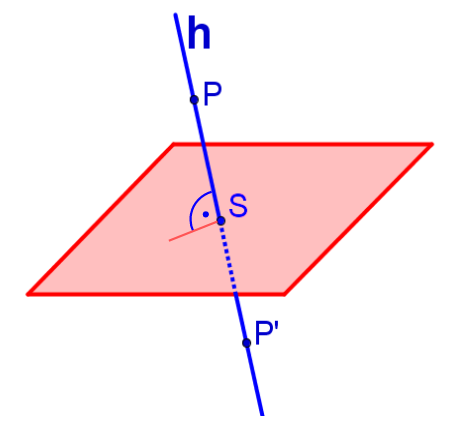
Gegeben sind der Punkt $P (- 1 | 7 | 2)$ und die Ebene $E : x_{1} + 3 x_{2} = 0$ .
Zeigen Sie, dass der Punkt $P$ nicht in $E$ liegt. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lagebeziehung Punkt-Ebene (Inzidenz)
Lösungsvorschlag
Setze die Koordinaten von $P$ in die Ebenengleichung ein:
$x_{1} + 3 x_{2}$ $=$ $0$
↓
Einsetzen
$- 1 + 3 \cdot 7$ $=$ $0$
↓
Zusammenfassen
$20$ $\neq$ $0$
Der Punkt liegt nicht in der Ebene.
Setze die $x_{1}, x_{2}, x_{3}$ Koordinaten von $P$ in die Ebene ein.
Vereinfache und überprüfe, ob die Gleichung erfüllt ist.

Bestimmen Sie die Koordinaten des Punktes, der entsteht, wenn $P$ an $E$ gespiegelt wird.
(4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Ebene spiegeln
Lösungsvorschlag
Hilfsgerade $h$
Die Hilfsgerade, die senkrecht zu $E$ und durch $P$ verläuft, hat die Parameterform:
$h : \vec{x} = \underset{= \vec{O P}}{\underset{⏟}{(\begin{array}{c} - 1 \\ 7 \\ 2 \end{array})}} + t \cdot \underset{= \vec{n} (Normalenvektor von E)}{\underset{⏟}{(\begin{array}{c} 1 \\ 3 \\ 0 \end{array})}}, t \in ℝ$
Skizze als Hilfe.
Schnittpunkt $S$
Die Hilfsgerade $h$ schneidet die Ebene $E$ .
Du bestimmst schrittweise den Schnittpunkt der Gerade mit einer Ebene, wenn du die Zeilen der Geradengleichung in die Ebene einsetzt.
$0$ $=$ $x_{1} + 3 x_{2}$
↓
$\begin{array}{l} x_{1} = - 1 + t \\ x_{2} = 7 + 3 t \end{array}$
$=$ $(- 1 + t) + 3 \cdot (7 + 3 t)$
↓
Vereinfachen
$=$ $- 1 + t + 21 + 9 t$
$=$ $10 t + 20$ $- 20$
↓
Gleichung nach $t$ umstellen
$- 20$ $=$ $10 t$ $: 10$
$t$ $=$ $- 2$
Du erhältst einen Wert t, mit dem der Richtungsvektor der Gerade multipliziert werden kann, um den Schnittpunkt S anzugeben:
Der Schnittpunkt hat damit den Ortsvektor: $\vec{O S} = (\begin{array}{c} - 1 \\ 7 \\ 2 \end{array}) - 2 \cdot (\begin{array}{c} 1 \\ 3 \\ 0 \end{array}) = (\begin{array}{c} - 3 \\ 1 \\ 2 \end{array})$
Addiere $\vec{O S}$ und den Verbindungsvektor $\vec{P S}$
Verschiebe $\vec{O S}$ um $\vec{P S}$
Der Verbindungsvektor $\vec{P S}$ ist: $\vec{P S} = (\begin{array}{c} - 3 \\ 1 \\ 2 \end{array}) - (\begin{array}{c} - 1 \\ 7 \\ 2 \end{array}) = (\begin{array}{c} - 2 \\ - 6 \\ 0 \end{array})$
Addiere $\vec{P S}$ zu $\vec{O S}$ für den Spiegelpunkt:
$\vec{O P^{'}}$ $=$ $\vec{O S} + \vec{P S}$
$=$ $(\begin{array}{c} - 3 \\ 1 \\ 2 \end{array}) + (\begin{array}{c} - 2 \\ - 6 \\ 0 \end{array})$
$=$ $(\begin{array}{c} - 5 \\ - 5 \\ 2 \end{array})$
Der gespiegelte Punkt hat die Koordinaten: $P^{'} (- 5 | - 5 | 2)$
Bestimme die Gleichung einer Hilfsgeraden, die senkrecht zur Ebene und durch $P$ verläuft.
Hierzu entnehme den Normalenvektor der Ebene aus der Koordinatenform $x_{1} + 3 x_{2} = 0$ .
Bestimme den Schnittpunkt $S$ der Hilfsgeraden und der Ebene.
Berechne den Verbindungsvektor $\vec{P S}$ und addiere diesen auf die Koordinaten des Schnittpunkts.
5
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe P5
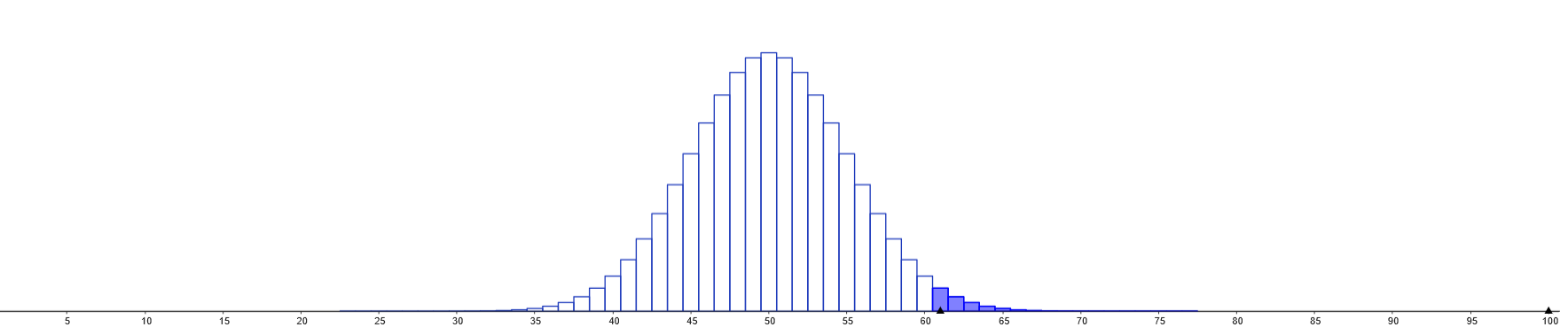
Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n = 100$ und $p$ .
Der Erwartungswert von $X$ ist 50.
Berechnen Sie die Standardabweichung von $X$ . (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Lösungsvorschlag
Wahrscheinlichkeit $p$
Eine binomialverteilte Zufallsvariable $X$ hat den Erwartungswert:
$μ$ $=$ $n \cdot p$
↓
Einsetzen der Informationen
$50$ $=$ $100 \cdot p$ $: 100$
$p$ $=$ $0,5$
Standardabweichung
Die Standardabweichung $σ$ einer lässt sich berechnen mit:
$σ$ $=$ $\sqrt{n \cdot p \cdot (1 - p)}$
↓
Einsetzen
$=$ $\sqrt{100 \cdot 0,5 \cdot 0,5}$
$=$ $5$
Die Standardabweichung beträgt $5$ .
Bestimme die Wahrscheinlichkeit $p$ des Zufallsexperiments über den gegebenen Erwartungswert.
Berechne die Standardabweichung.

Die Wahrscheinlichkeit $P (X \geq 61)$ beträgt etwa $2 %$ .
Bestimmen Sie damit einen Näherungswert für die Wahrscheinlichkeit $P (40 \leq X \leq 60)$ .
(2 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomialverteilung
Lösungsvorschlag
Darstellung einer Binomialverteilung mit $n = 100$ und Erwartungswert $50$ .
Eine Binomialverteilung mit $n = 100$ und $μ = 50$ ist wegen $p = 0,5$ symmetrisch um den Erwartungswert.
Wenn
$P (X \geq 61) \approx 0,02$
beträgt, dann gilt auch für die Wahrscheinlichkeit
$P (X \leq 39) \approx 0,02.$
Die Wahrscheinlichkeit muss insgesamt $1$ betragen. Damit ist:
$P (40 \leq X \leq 60) \approx 1 - 0,02 - 0,02 = 0,96$
Die Wahrscheinlichkeit, dass $X$ mindestens 40 und höchstens 60 ist, ist etwa $96 %$ .
Bestimme die Wahrscheinlichkeit $P (X \geq 39)$ .
Verwende hierzu, dass die Verteilung näherungsweise symmetrisch ist.
Berechne $P (40 \leq X \leq 60)$ .
6
Niedersächsisches Kultusministerium (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Kultusministerium Niedersachsen zur Verfügung gestellt --- Die Lösungsvorschläge dagegen sind NICHT vom Land Niedersachsen
Aufgabe P6
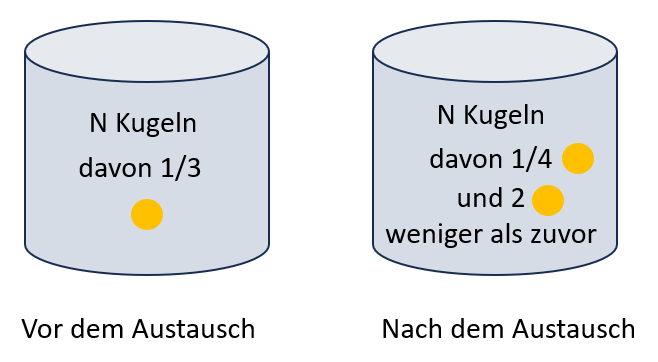
In einem Behälter befinden sich Kugeln, von denen jede dritte gelb ist.
Aus dem Behälter wird zweimal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt.
Berechnen Sie die Wahrscheinlichkeit dafür, dass beide Kugeln gelb sind. (1 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Laplace-Experiment
Lösungsvorschlag
Wahrscheinlichkeit für gelb
Jede dritte Kugel ist gelb: $p = \frac{Anzahl gelbe Kugeln}{Anzahl gesamte Kugeln} = \frac{1}{3}$
Wahrscheinlichkeit für "2 mal gelb"
Beim 2-maligen Ziehen verwendest du die Pfadregeln: $P (" 2 mal gelb ") = \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{9}$
Bestimme die Wahrscheinlichkeit dafür, eine gelbe Kugel zu ziehen.
Berechne die Wahrscheinlichkeit für das Ereignis "Zwei mal gelb"
Beachte, dass zwischen den Ziehungen zurückgelegt wird.

Im Behälter werden zwei gelbe Kugeln durch zwei blaue Kugeln ersetzt. Anschließend wird aus dem Behälter erneut zweimal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt. Die Wahrscheinlichkeit dafür, dass beide Kugeln gelb sind, beträgt nun $\frac{1}{16}$ .
Ermitteln Sie, wie viele gelbe Kugeln sich nach dem beschriebenen Vorgang im
Behälter befinden. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wahrscheinlichkeit
Lösungsvorschlag
Die Wahrscheinlichkeit $\frac{1}{16} = \underset{2 mal gelb}{\underset{⏟}{\frac{1}{x} \cdot \frac{1}{x}}}$ lässt darauf schließen, dass nun jede 4. Kugel gelb sein muss.
Vorüberlegung
$n$ ist die gesuchte Anzahl gelber Kugeln nach dem Tausch
$N$ ist die Gesamtzahl der Kugeln.
Anteil vor dem Austausch
Vor dem Tausch gab es zwei gelbe Kugeln mehr:
$\frac{n + 2}{N} = \frac{1}{3}$

Nach dem Austausch
$\frac{n}{N} = \frac{1}{4}$
Diese Gleichung ergibt umgeformt: $N = 4 \cdot n$
Anzahl der gelben Kugeln
Bestimme die Anzahl $n$ mithilfe der ersten Gleichung.
$\frac{n + 2}{N}$ $=$ $\frac{1}{3}$
↓
Einsetzen $N = 4 \cdot n$
$\frac{n + 2}{4 \cdot n}$ $=$ $\frac{1}{3}$ $\cdot 4 n$
$n + 2$ $=$ $\frac{4}{3} n$ $- n$
$2$ $=$ $\frac{1}{3} n$ $\cdot 3$
$6$ $=$ $n$
Nach dem Tausch sind es $n = 6$ gelbe Kugeln.
Stelle eine Gleichung auf mit der Wahrscheinlichkeit $P ($ "2 mal gelb" $)$ $= \frac{1}{16}$
Es hilft dabei, die gesuchte Anzahl $x$ zu nennen.
Bestimme den Anteil der gelben Kugel nach dem Austausch
Vor dem Austausch und nach dem Austausch lassen sich die Anteile der gelben Kugeln mit Gleichungen ausdrücken.
Stelle diese Gleichungen auf
Bestimme die Anzahl der gelben Kugeln nach dem Austausch

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$0$	$=$	$2 x \cdot (2 x^{2} - k)$
	↓	Für $x \neq 0$ ist die Gleichung gelöst, wenn:
$0$	$=$	$2 x^{2} - k$	$+ k$
$k$	$=$	$2 x^{2}$	$: 2$
$\frac{k}{2}$	$=$	$x^{2}$	$\pm \sqrt{}$
$x_{1}$	$=$	$\sqrt{\frac{k}{2}}$
$x_{2}$	$=$	$- \sqrt{\frac{k}{2}}$

$h (- x)$	$=$	$f (- x) \cdot (g (- x))^{3}$
	↓	$f$ ist y-Achsen-symmetrisch
	$=$	$f (x) \cdot (g (- x))^{3}$
	↓	$g$ ist punktsymmetrisch zum Urpsrung
	$=$	$f (x) \cdot (- g (x))^{3}$
	↓	Potenzgesetze
	$=$	$f (x) \cdot (- 1) \cdot g (x)^{3}$
	$=$	$- \underset{= h (x)}{\underset{⏟}{f (x) \cdot g (x)^{3}}}$
	$=$	$- h (x)$

Pflichtteil

Aufgabe P1

Ableitung mit der Regel für Potenzfunktionen:

Lösungsvorschlag

Aufgabe P2

Grenzen der Integration

Wert des Integrals

Aufgabe P3

Extrempunkt von $f$

Extrempunkt von $g$

Setze für $x$ den Term $- x$ ein

Aufgabe P4

Lösungsvorschlag

Lösungsvorschlag

Aufgabe P5

Lösungsvorschlag

Lösungsvorschlag

Aufgabe P6

Lösungsvorschlag

Lösungsvorschlag

$f (x)$	$=$	$x^{4} - k \cdot x^{2}$
	↓	Exponent kommt herunter, neuer Exponent wird um $1$ kleiner.
$f^{'} (x)$	$=$	$4 \cdot x^{3} - k \cdot 2 \cdot x^{1}$
	↓	$x^{1} = x$
	$=$	$4 x^{3} - 2 k x$
	↓	Ausklammern von $2 x$
	$=$	$2 x \cdot (2 x^{2} - k)$

$f (\sqrt{\frac{k}{2}})$	$=$	$- 1$
	↓	Einsetzen in den Funktionsterm
${(\sqrt{\frac{k}{2}})}^{4} - k \cdot {(\sqrt{\frac{k}{2}})}^{2}$	$=$	$- 1$
$\frac{k^{2}}{4} - k \cdot \frac{k}{2}$	$=$	$- 1$
	↓	$\frac{k^{2}}{4} - \frac{k^{2}}{2} = - \frac{k^{2}}{4}$
$- \frac{k^{2}}{4}$	$=$	$- 1$	$\cdot (- 1)$
$\frac{k^{2}}{4}$	$=$	$1$	$\cdot 4$
$k^{2}$	$=$	$4$	$\sqrt{}$
	↓	$k$ soll eine positive Zahl sein. Der negative Wert ist keine Lösung.
$k$	$=$	$2$

$f (x)$	$=$	$\sin (x)$
	↓	Ableitung von Sinus
$f^{'} (x)$	$=$	$\cos (x)$
$f^{'} (0)$	$=$	$\cos (0)$
	$=$	$1$

$A$	$=$	$\int_{0}^{\frac{π}{2}} x - \sin (x) d x$
	↓	Stammfunktion bestimmen
	$=$	${[\frac{1}{2} x^{2} + \cos (x)]}_{0}^{\frac{π}{2}}$
	↓	Grenzen einsetzen
	$=$	$\frac{1}{2} {(\frac{π}{2})}^{2} + \cos (\frac{π}{2}) - (\frac{1}{2} \cdot 0^{2} + \cos (0))$
	↓	Zusammenfassen
	$=$	$\frac{π^{2}}{8} + 0 - 1$
	↓	Gesamtfläche ist das Doppelte.
$A_{ges}$	$=$	$\underset{Fläche doppelt nehmen (Symmetrie)}{\underset{⏟}{2}} \cdot A$
	$=$	$2 \cdot (\frac{π^{2}}{8} - 1)$
	$=$	$\frac{π^{2}}{4} - 2$

$x_{1} + 3 x_{2}$	$=$	$0$
	↓	Einsetzen
$- 1 + 3 \cdot 7$	$=$	$0$
	↓	Zusammenfassen
$20$	$\neq$	$0$

$0$	$=$	$x_{1} + 3 x_{2}$
	↓	$\begin{array}{l} x_{1} = - 1 + t \\ x_{2} = 7 + 3 t \end{array}$
	$=$	$(- 1 + t) + 3 \cdot (7 + 3 t)$
	↓	Vereinfachen
	$=$	$- 1 + t + 21 + 9 t$
	$=$	$10 t + 20$	$- 20$
	↓	Gleichung nach $t$ umstellen
$- 20$	$=$	$10 t$	$: 10$
$t$	$=$	$- 2$

$\vec{O P^{'}}$	$=$	$\vec{O S} + \vec{P S}$
	$=$	$(\begin{array}{c} - 3 \\ 1 \\ 2 \end{array}) + (\begin{array}{c} - 2 \\ - 6 \\ 0 \end{array})$
	$=$	$(\begin{array}{c} - 5 \\ - 5 \\ 2 \end{array})$

$μ$	$=$	$n \cdot p$
	↓	Einsetzen der Informationen
$50$	$=$	$100 \cdot p$	$: 100$
$p$	$=$	$0,5$

$σ$	$=$	$\sqrt{n \cdot p \cdot (1 - p)}$
	↓	Einsetzen
	$=$	$\sqrt{100 \cdot 0,5 \cdot 0,5}$
	$=$	$5$

$\frac{n + 2}{N}$	$=$	$\frac{1}{3}$
	↓	Einsetzen $N = 4 \cdot n$
$\frac{n + 2}{4 \cdot n}$	$=$	$\frac{1}{3}$	$\cdot 4 n$
$n + 2$	$=$	$\frac{4}{3} n$	$- n$
$2$	$=$	$\frac{1}{3} n$	$\cdot 3$
$6$	$=$	$n$

Pflichtteil

Aufgabe P1

Ableitung mit der Regel für Potenzfunktionen:

Lösungsvorschlag

Aufgabe P2

Grenzen der Integration

Wert des Integrals

Aufgabe P3

Extrempunkt von f

Extrempunkt von g

Setze für x den Term −x ein

Aufgabe P4

Lösungsvorschlag

Lösungsvorschlag

Aufgabe P5

Lösungsvorschlag

Lösungsvorschlag

Aufgabe P6

Lösungsvorschlag

Lösungsvorschlag

Extrempunkt von $f$

Extrempunkt von $g$

Setze für $x$ den Term $- x$ ein