Geraden im dreidimensionalen Raum

Inhalt des Kurses:

In diesem Kurs lernst du die grundlegenden Eigenschaften von Geraden im dreidimensionalen Raum.

Vorkenntnisse:

Du solltest sowohl die Grundbegriffe Vektor, als auch Gerade verstanden haben und dich im dreidimensionalen Koordinatensystem zurecht finden.

Kursdauer:

Die Länge des Kurses beträgt ungefähr $45$ min.

Stelle dir einen beliebigen Vektor in einem dreidimensionalen Raum vor. Du weißt bereits, dass dieser im Raum gerichtet ist. Das heißt er zeigt in eine eindeutige Richtung und hat eine feste Länge, aber keine feste Lage im Raum.

Wenn du zum Beispiel den Vektor $\overrightarrow{a}=\left(\begin{array}{c}-1\\ 2\\ 1\end{array}\right)$ anschaust, hat dieser keine feste Lage.

Er könnte einen Repräsentanten zwischen den Punkten $A(-2|-3|1)$ und $B(-3|-1|2)$ oder zwischen $C(-2|3|1)$ und $D(-3|5|2)$ haben, weil bei beiden der Verbingungsvektor dem Vektor $\overrightarrow{a}$ entspricht $(\overrightarrow{AB}=\overrightarrow{CD}=\overrightarrow{a})$.

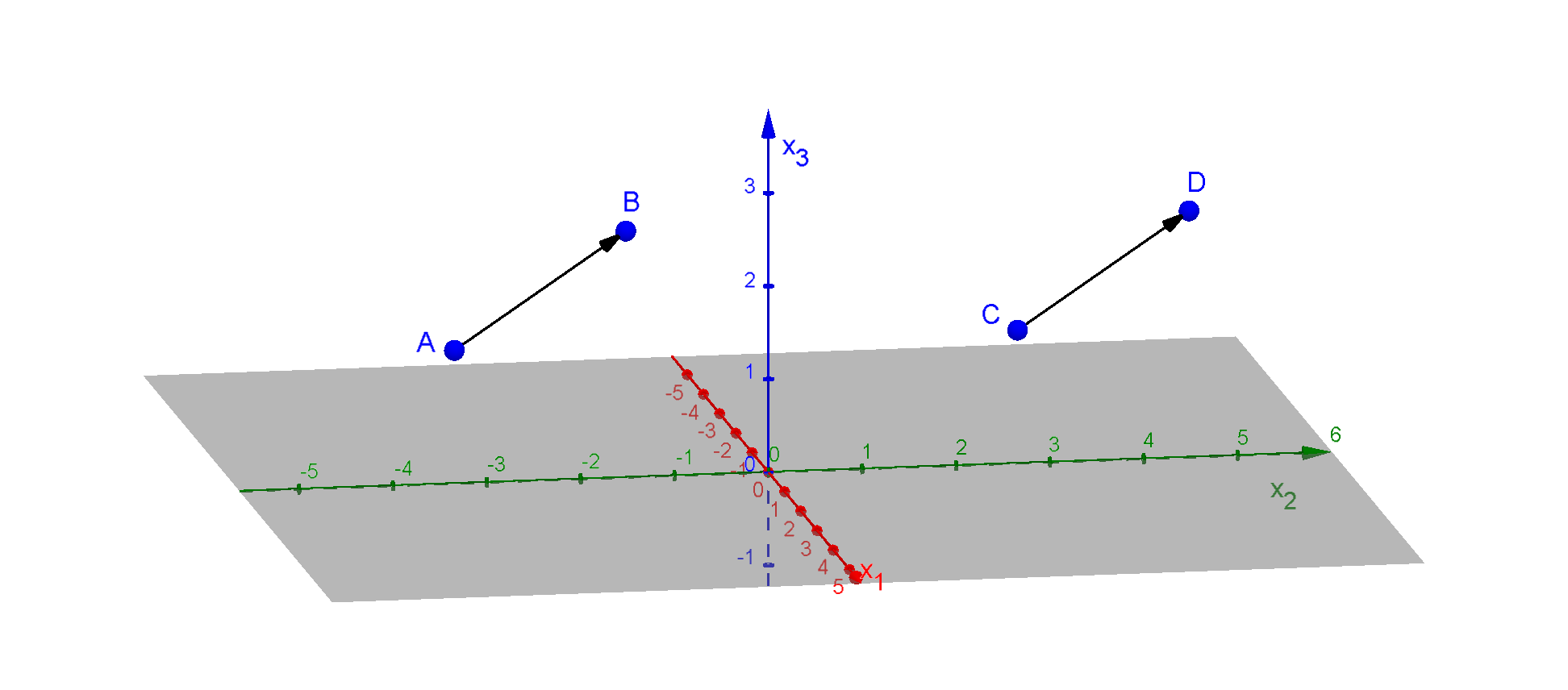
Würdest du nun den Vektor $\overrightarrow{a}$ beliebig oft aneinander hängen erhältst du einen beliebig langen geraden Vektor, aber keine Gerade. Du weißt bereits aus dem $2$-dimensionalen, dass eine Gerade immer fest im Raum liegt.

Du kennst bereits den Begriff der Gerade aus dem $2$-dimensionalen. Eine Gerade ist eine Menge von Punkten, die die Geradengleichung erfüllen, das heißt insbesondere dass die Gerade fest im Raum liegt, da jedes $x$ in der Geradengleichung einen Punkt $y$ zugeordnet bekommt und diese dann die Koordinaten der einzelnen Punkte der Gerade sind. Zum Beispiel für eine Gerade $g(x)=2\cdot x+1$ liegt der Punkt $P(2|5)$ auf der Geraden, denn $2\cdot 2+1=5=y$.

Ein Beispiel aus dem $2$-dimensionalen:

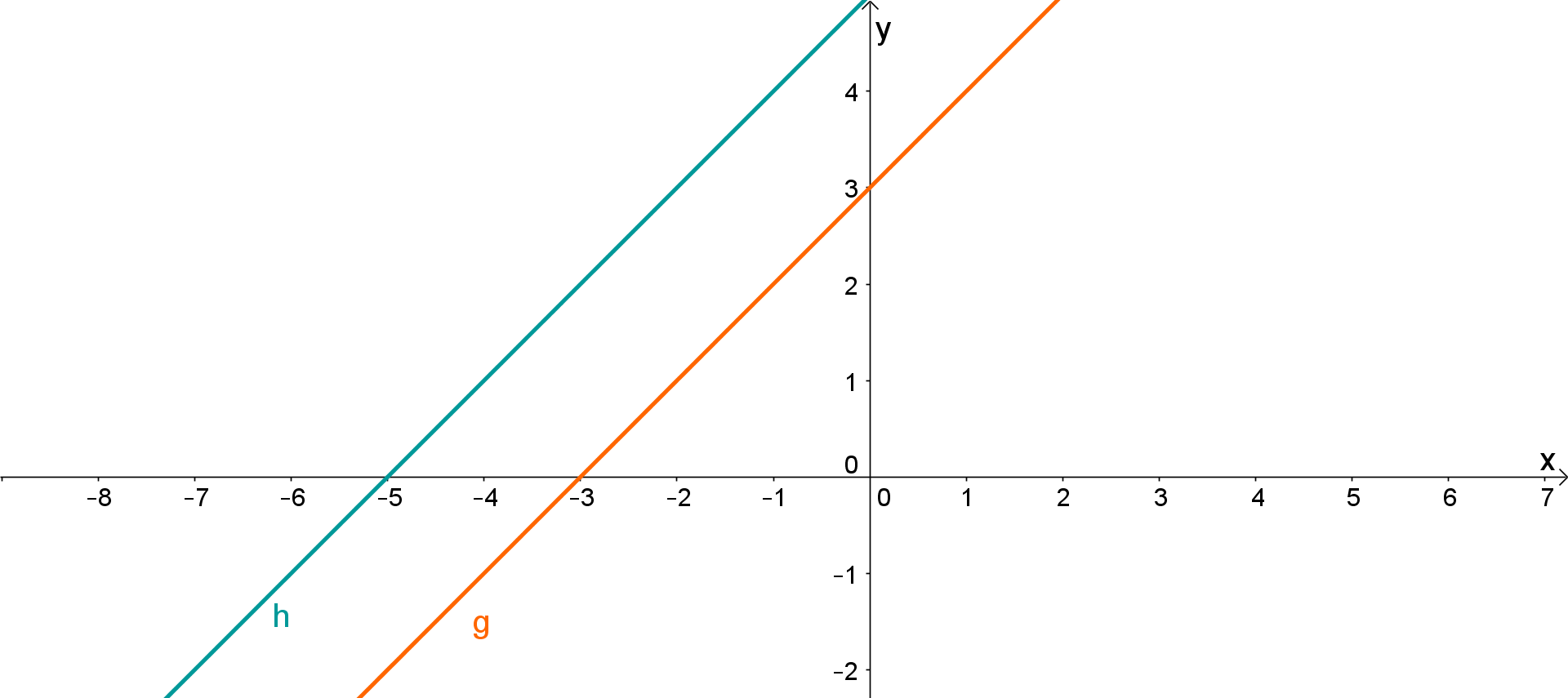
Die beiden Geraden $g$ und $h$ laufen in die selbe Richtung, haben aber nicht die gleiche Lage und sind somit verschieden.

Wie auf der vorherigen Seite angesprochen könntest du einen Vektor beliebig oft aneinander hängen und hättest so eine unendlich lange gerade Linie, jedoch keine Gerade.

Wenn du nun aber dir einen Startpunkt auswählst und von diesem aus den Vektor beliebig oft aneinander hängst, wird dein unendlicher langer Vektor an diesen Punkt fixiert und du kannst ihn nicht mehr beliebig im Raum verschieben, da er abhängig von diesem Punkt ist.

Du hast nun eine Gerade im $3$-dimensionalen Raum und nennst diesen Punkt der den Vektor fixiert Aufpunkt der Gerade.

Du weißt bereits, dass eine Gerade einen sogenannten Aufpunkt braucht, welcher die Gerade im Raum fixiert. Möchtest du nun die dazugehörige Geradengleichung aufstellen, gibt es $2$ Möglichkeiten. Entweder du hast $2$ Punkte, einen Aufpunkt und einen weiteren durch den du die Gerade legen möchtest, oder du hast einen Punkt und einen Vektor, also einen Aufpunkt und einen Vektor der dir bereits die Richtung deiner Gerade vorgibt.

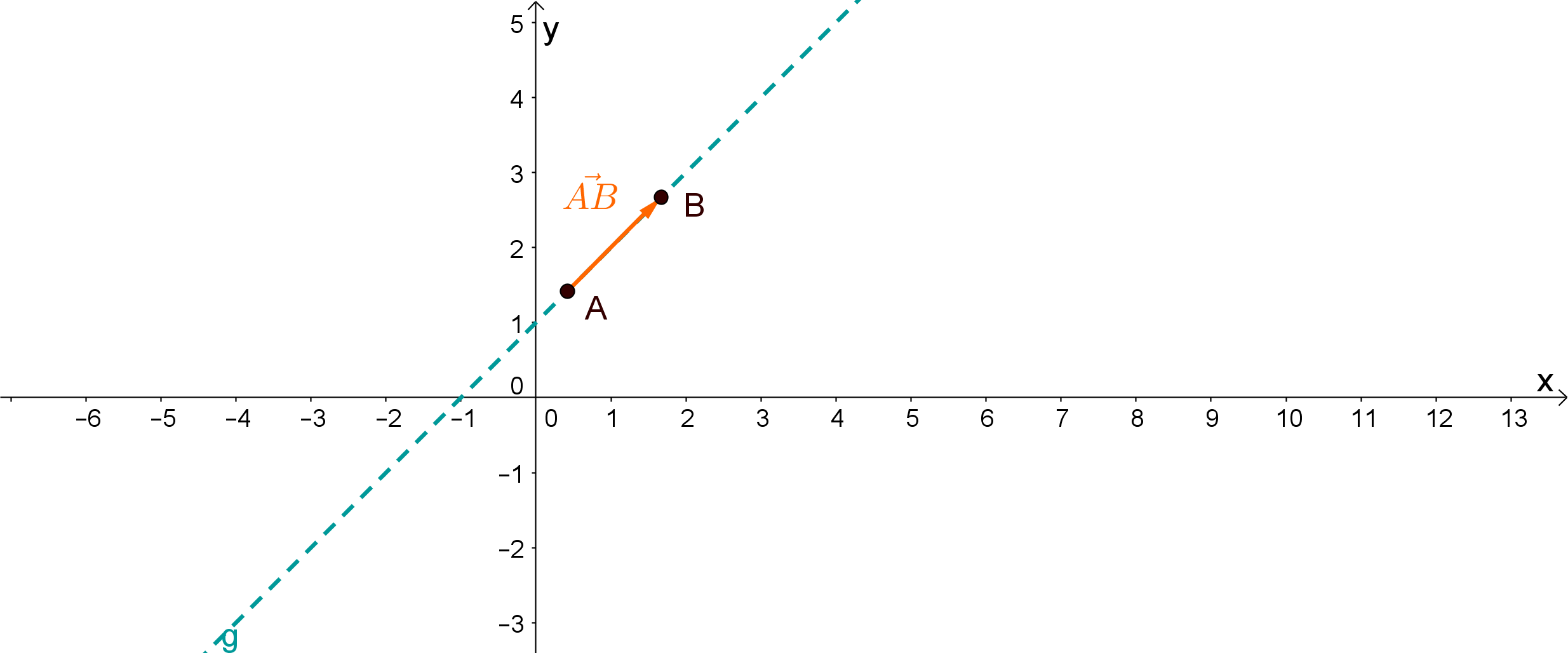
1.Gerade durch zwei Punkte $A$ und $B$:

Wähle als Aufpunkt den Punkt $\overrightarrow{A}$. Da die Gerade durch beide Punkte gehen soll, überlegst du dir wie du zu dem Punkt $\overrightarrow{B}$ von $\overrightarrow{A}$ aus kommst. Dazu musst du zu A den Verbindungsvektor von $\overrightarrow{A}$ und $\overrightarrow{B}$, nämlich $\overrightarrow{AB}$ dazuzählen. Wenn du den Verbindungsvektor $\overrightarrow{AB}$ $1$ mal dazu zählst, erhälst du den Punkt $\overrightarrow{B}$, nachdem du aber eine Gerade durch $\overrightarrow{A}$ und $\overrightarrow{B}$ aufstellen möchtest addierst du den Verbindungsvektor beliebig oft dazu, denn so kannst du jeden Punkt auf der Gerade durch $\overrightarrow{A}$ und $\overrightarrow{AB}$ erreichen. Das beliebigofte dazuzählen des Vektors drückst du durch eine Variable aus, also die Variable mal den Vektor. In der Regel nimmst du dafür Variablen wie $\lambda$ oder $\mu$. Für die Variable darfst du Werte aus $ℝ$ einsetzen.

Die vollständige Geradengleichung lautet also:

$g:\overrightarrow{X}=\overrightarrow{A}+\lambda \cdot \overrightarrow{AB}$

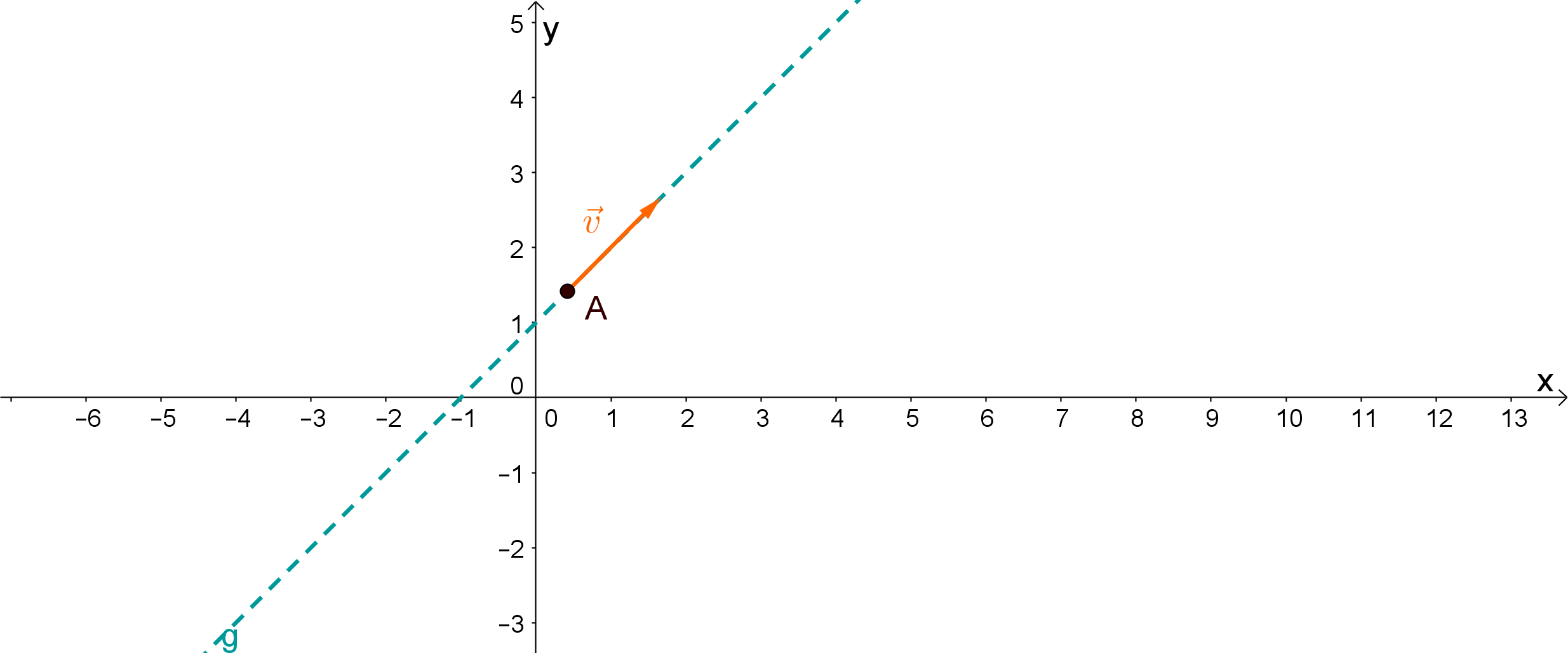
2.Gerade durch einen Punkt $\overrightarrow{A}$ und mit einem Richtungsvektor $\overrightarrow{v}$:

Wähle wieder den Aufpunkt $\overrightarrow{A}$ und addiere zu ihm $\lambda$ mal den Richtungsvektor, denn so erreichst du alle Punkte die in der angegebenen Richtung gesucht sind, weil du für $\lambda$ wieder alle Werte aus $ℝ$einsetzen kannst.

$g:\overrightarrow{X}=\overrightarrow{A}+\lambda \cdot \overrightarrow{v}$

Stelle die Geradengleichung für die Gerade $g$ auf, die durch die Punkte $A(2|1|4)$ und $B(-1|3|2)$ läuft.

1. Wähle als Aufpunkt für die Gerade den Punkt $\overrightarrow{A}$ aus.

2. Berechne nun den Verbindungsvektor $\overrightarrow{AB}$.

3. Stelle die Geradengleichung auf.

Zu 1.)

Aufpunkt der Geradengleichung ist $\overrightarrow{A}=\left(\begin{array}{c}2\\ 1\\ 4\end{array}\right)$

Zu 2.)

Zu 3.)

Stelle die Geradengleichung für die Gerade $h$ auf, die durch den Punkt $A(1|3|2)$ läuft und die Richtung $\overrightarrow{v}=\left(\begin{array}{c}1\\ 2\\ 1\end{array}\right)$ hat.

1. Wähle als Aufpunkt für die Gerade den Punkt $\overrightarrow{A}$ aus.

2. Stelle die Geradengleichung auf.

Zu 1.)

Aufpunkt der Geradengleichung ist $\overrightarrow{A}=\left(\begin{array}{c}1\\ 3\\ 2\end{array}\right)$

Zu 2.)

$h:\overrightarrow{X}=\overrightarrow{A}+\lambda \cdot \overrightarrow{v}=\left(\begin{array}{c}1\\ 3\\ 2\end{array}\right)+\lambda \cdot \left(\begin{array}{c}1\\ 2\\ 1\end{array}\right)$

Um eine Geradengleichung aufzustellen brauchst du immer einen Aufpunkt und einen Richtungsvektor. Der Richtungsvektor ist entweder bereits angegeben oder du musst den Verbindungsvektor zwischen $2$ Punkten aufstellen.

Wenn du den Aufpunkt und einen Richtungsvektor hast, addierst du den Richtungsvektor $\lambda$ mal zu dem Aufpunkt dazu und erhältst eine Geradengleichung.