Aufgaben zur Kurvendiskussion

Setze hier alle Bestandteile zusammen und übe mit Aufgaben zur Kurvendiskussion.

Es ist folgende Funktion gegeben:

f (x) = \frac{(2 x^{2} - 2) \cdot \ln ({(x - 1)}^{2})}{1 + x}

In den Teilaufgaben findest du alles, was du für diese Funktion berechnen könntest.

Suche dir das heraus, was du üben möchtest.

Bei späteren Teilaufgaben kann auf frühere Ergebnisse zurückgegriffen werden.

Ist dir nicht sofort klar, woher diese Ergebnisse kommen, dann bearbeite zunächst diese früheren Teilaufgaben zur Wissensauffrischung.

Bestimme den Definitionsbereich und die Art der Definitionslücken.

Definitionsbereich
Der Definitionsbereich ist der Zahlenbereich, der für die Funktion zulässig ist. Um ihn zu bestimmen gehst du von den reellen Zahlen $ℝ$ aus und überprüfst, welche Zahlen nicht in die Funktion eingesetzt werden dürfen.
Die Funktion ist eine Kombination aus einem Bruch, Polynomen und einer Logarithmusfunktion. Bei Polynomen darf man für $x$ ganz $ℝ$ einsetzen. Bei Brüchen darf der Nenner nicht 0 sein. Logarithmen darf man nur von positiven Zahlen nehmen.
Der Nenner darf nicht Null werden.
Setze den Nenner $1 + x$ gleich $0$ , um herauszufinden, welche Zahl nicht für $x$ eingesetzt werden darf.
$1 + x$ $=$ $0$ $- 1$
$x$ $=$ $- 1$
$x = - 1$ ist eine Definitionslücke.
Das Argument des Logarithmus muss größer als 0 sein.
Setze $(x - 1)^{2} > 0$ .
Da Quadratische Funktionen nicht negativ sind, musst du nur ausschließen, dass der Term 0 wird.
${(x - 1)}^{2}$ $=$ $0$ $\sqrt{}$
↓
Ziehe die Wurzel.
$x - 1$ $=$ $0$ $+ 1$
$x$ $=$ $1$
$x = 1$ ist eine Definitionslücke.
Definitionsmenge
$D_{f} = ℝ ∖ {- 1; 1}$
Art der Definitionslücken
Es gibt zwei Arten von Definitionslücken: hebbare und nicht hebbare.
Hebbare Definitionslücken liegen dann vor, wenn die Funktion an jenen Stellen stetig fortsetzbar sind. Das ist zum Beispiel bei Brüchen der Fall, wenn die Nennernullstelle zugleich eine Zählernullstelle ist.
Definitionslücke $x = - 1$
Um das zu überprüfen, setzt du die oben bestimmte Nennernullstelle in den Zähler ein:
$(2 {(- 1)}^{2} - 2) \cdot \ln ({((- 1) - 1)}^{2}) = 0 \cdot \ln (4) = 0$
Die Nennernullstelle $- 1$ ist also eine Zählernullstelle und damit eine hebbare Definitionlücke.
Definitionslücke $x = 1$
Als nächstes willst du die Art der Definitionslücke von $1$ herausfinden. Dabei kannst du nicht analog zu oben argumentieren, da in diesem Fall die Lücke durch die Logarithmusfunktion verursacht wird.
Du musst zeigen, dass die Funktion an der Stelle $1$ entweder stetig fortsetzbar ist oder nicht.
Falls die Funktion von rechts und von links an die $1$ angenähert den selben endlichen Wert annehmen, dann ist die Funktion stetig fortsetzbar und damit eine hebbare Definitionslücke.
Du überprüfst:
$\lim_{x \to 1 +} f (x) = \lim_{x \to 1 +} \frac{\overset{= 0}{(2 x^{2} - 2)} \cdot \overset{= - \infty}{\ln}}{\underset{= 2}{1}} \overset{Polynom stärker}{\underset{als Logarithmus}{=}} 0$
Alternativ kannst du auch mit den Regeln von Regeln von L'Hospital argumentieren.
Analog gilt:
$\lim_{x \to 1 -} f (x) = 0$
Es folgt insgesamt, dass $1$ ebenfalls eine hebbare Definitionslücke ist.

Vereinfache die Funktionsgleichung.

Berechne die Grenzwerte an den Rändern des Definitionsbereichs.

Setze die Funktion $f$ - wenn möglich - stetig zu einer Funktion $\hat{f}$ fort.

Will man eine Funktion stetig fortsetzen, dann muss man die Funktion an allen Unstetigkeitsstellen - und nur dort - neu definieren.
Deswegen erhält man dann eine abschnittsweise definierte Funktion.
Hier hast du:
$f (x) = 2 (x - 1) \cdot \ln ({(x - 1)}^{2})$
Diese Funktion hat Definitionslücken bei -1 und 1 und damit dort auch Unstetigkeitsstellen.
Beide sind keine Polstellen, sondern behebbare Definitionslücken, also ist die Funktion stetig fortsetzbar.
Für die kritischen Punkte gilt
$\begin{array}{ll} \lim_{x \to - 1} f (x) & = - 4 \ln (4) \\ \lim_{x \to 1} f (x) & = 0 \end{array}$
Nun definierst du die Funktion neu und setzt an den kritischen Stellen jeweils den Grenzwert ein:
$\hat{f} (x) = {\begin{array}{lcl} - 4 \cdot \ln (4) & für & x = - 1 \\ 0 & für & x = 1 \\ f (x) & sonst \end{array}$
Die Funktion $\hat{f}$ ist jetzt die stetig fortgesetzte Version von $f$ ohne Lücken.
Bestimme die Asymptoten.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Asymptote
Es gibt waagerechte, senkrechte und schiefe Asymptoten .
Waagerechte Asymptoten treten auf, wenn ein Grenzwert im Unendlichen einen konkreten Zahlenwert liefert.
Senkrechte Asymptoten treten auf, wenn der Grenzwert an Definitionslücken keinen konkreten Zahlenwert, sondern $\pm \infty$ liefert.
Schiefe Asymptoten treten manchmal bei Bruchtermen auf.
Waagerechte Asymptoten
Die Grenzwerte im Unendlichen sind $\infty$ . Deshalb gibt es keine waagerechten Asymptoten.
Senkrechte Asymptoten
Die Grenzwerte an den Definitionslücken sind $- 4 \ln (4)$ und $0$ . Deshalb gibt es keine senkrechten Asymptoten.
Schiefe Asymptoten
Schiefe Asymptoten können nur bei gebrochen-rationalen Funktionen vorkommen (also ohne den Logarithmus). Deshalb gibt es keine schiefen Asymptoten.
Bestimme die Nullstellen.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstellen
Nullstellen sind diejenigen Punkte, an denen der y-Wert den Wert 0 annimmt.
Zur Berechnung musst du die Funktion nur gleich 0 setzen.
$f (x)$ $=$ $0$
$2 (x - 1) \ln ({(x - 1)}^{2})$ $=$ $0$
Ein Produkt ist $0$ , wenn einer der Faktoren $0$ ist. Setze also die Faktoren des Terms gleich $0$ .
$x - 1 = 0$ gilt, wenn $x = 1$ ist.
$\ln ((x - 1)^{2}) = 0$ , wenn $(x - 1)^{2} = 1$ ist $\Rightarrow x = 0$ oder $x = 2$
Da aber $1 \notin 𝔻_{f}$ , hat die Funktion nur zwei Nullstellen:
${Nst}_{1} (0 | 0)$ und ${Nst}_{2} (2 | 0)$

Bestimme die Extrempunkte.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrempunkte

Extremstellen sind die Stellen des Funktionsgraphen, bei denen der Graph nicht steigt oder fällt. Die Steigung des Funktionsgraphen berechnet man über die Ableitung der Funktion. Soll die Steigung 0 sein, so musst du die Ableitung gleich 0 setzen. Damit erhältst du die Lage der Extremstellen.

Extremstelle berechnen

$f (x) = 2 (x - 1) \cdot \ln ({(x - 1)}^{2})$

Für die Ableitung dieser Funktion brauchst du die Produktregel und die Kettenregel.

Bei der Kettenregel leitest du die Funktionen von außen nach innen ab, also zuerst den Logarithmus, dann die quadrierte Klammer und zum Schluss das $x$ , das als Ableitung 1 liefert.

$f^{'} (x)$	$=$	$2 \cdot \ln ({(x - 1)}^{2}) + 2 \cdot (x - 1) \cdot \frac{2 \cdot (x - 1)}{{(x - 1)}^{2}}$
	↓	Kürze den zweiten Summanden mit $(x - 1)^{2}$ .
	$=$	$2 \cdot \ln ({(x - 1)}^{2}) + 4$
	$=$	$2 \cdot (\ln ({(x - 1)}^{2}) + 2)$

Jetzt musst du diesen Ausdruck gleich 0 setzen.

$f^{'} (x)$	$=$	$0$
$2 \cdot (\ln ({(x - 1)}^{2}) + 2)$	$=$	$0$	$: 2$
$\ln ({(x - 1)}^{2}) + 2$	$=$	$0$	$- 2$
$\ln ({(x - 1)}^{2})$	$=$	$- 2$
	↓	Löse den Logarithmus mithilfe der e-Funktion auf.
$e^{\ln ({(x - 1)}^{2})}$	$=$	$e^{- 2}$
${(x - 1)}^{2}$	$=$	$\frac{1}{e^{2}}$
${(x - 1)}^{2}$	$=$	${(\frac{1}{e})}^{2}$	$\sqrt{}$
	↓	Ziehe die Wurzel.
$x - 1$	$=$	$\pm \frac{1}{e}$	$+ 1$
$x$	$=$	$1 \pm \frac{1}{e}$

Jetzt hast du die Lage ( $x$ - Werte) der Extrempunkte bestimmt. Beide liegen im Definitionsbereich. Für die $y$ - Werte musst du nun die erhaltenen $x$ - Werte in die Funktion $f (x)$ einsetzen.

Koordinaten der Extrempunkte

$\begin{array}{rcl} f (1 - \frac{1}{e}) & = & 2 (1 - \frac{1}{e} - 1) \cdot \ln ({(1 - \frac{1}{e} - 1)}^{2}) \\ = & - \frac{2}{e} \cdot \ln (\frac{1}{e^{2}}) = - \frac{2}{e} \cdot (- 2) \ln (e) \\ = & \frac{4}{e} \end{array}$

$\Rightarrow {EP}_{1} (1 - \frac{1}{e} | \frac{4}{e})$

$\begin{array}{rcl} f (1 + \frac{1}{e}) & = & 2 (1 + \frac{1}{e} - 1) \cdot \ln ({(1 + \frac{1}{e} - 1)}^{2}) \\ = & \frac{2}{e} \cdot \ln (\frac{1}{e^{2}}) = \frac{2}{e} \cdot (- 2) \ln (e) \\ = & - \frac{4}{e} \end{array}$

$\Rightarrow {EP}_{2} (1 + \frac{1}{e} | - \frac{4}{e})$

Art der Extrempunkte bestimmen

Nachdem du die Koordinaten bestimmt hast, fehlt nur noch die Art der Extrempunkte.

Diese lässt sich entweder durch das Überprüfen des Monotonieverhaltens im Definitionsbereich oder durch einsetzen der $x$ - Werte der Extrema in die 2. Ableitung bestimmen.

Für ein Minimum $x_{\min}$ gilt: $f^{'} (x_{\min}^{-}) < 0 \land f^{'} (x_{\min}^{+}) > 0$ bzw. meistens $f^{''} (x_{\min}) > 0$ .
Für ein Maximum $x_{\max}$ gilt: $f^{'} (x_{\max}^{-}) > 0 \land f^{'} (x_{\max}^{+}) < 0$ bzw. meistens $f^{''} (x_{\max}) < 0$ .
Für einen Terrassenpunkt gilt: $f^{'} ({x_{TP}}^{-}) < 0 \land f^{'} ({x_{TP}}^{+}) > 0 \lor f^{'} ({x_{TP}}^{-}) > 0 \land f^{'} ({x_{TP}}^{+}) < 0$ bzw. meistens $f^{''} (x_{TP}) = 0 \land f^{'''} (x_{TP}) \neq 0$ .

Für eine Erklärung der Zeichen sieh dir den Artikel Logikverknüpfungen an.

Um unabhängig von einer möglicherweise komplizierten 2. Ableitung zu bleiben, überprüfst du hier am Besten das Monotonieverhalten.

Art der Extrempunkte (formal)

Hier ist $1 - {(\frac{1}{e})}^{-}$ minimal kleiner als $1 - \frac{1}{e}$ .

Diese kleine Abweichung wird die ganze Rechnung mitgezogen.

$\begin{array}{l} f^{'} ({(1 - \frac{1}{e})}^{-}) \\ = 2 (\ln ({(1 - {\frac{1}{e}}^{+} - 1)}^{2}) + 2) \\ = 2 (\ln ({\frac{1}{e^{2}}}^{-}) + 2) \\ = 2 \underset{> 0}{\underset{⏟}{(\underset{> - 2}{\underset{⏟}{- 2 \underset{< 1}{\underset{⏟}{\ln (e^{-})}}}} + 2)}} > 0 \end{array}$

Beachte, dass die kleine Abweichung je nach Klammersetzung und beim Quadrieren die Richtung ändert! Diese kleinliche und unanschauliche Vorgehensweise müsste man für jeden Punkt zwei mal durchführen. In der Schule reicht es meistens einfacher:

Da du ausgerechnet hast, dass es nur 2 Extrema gibt, muss der Graph dazwischen entweder die ganze Zeit steigen oder fallen (falls keine Polstelle dazwischen liegt!). Deshalb musst du nicht nicht so nahe an der Extremstelle die Steigung überprüfen - es reicht ein Punkt auf dem Weg zum nächsten Extremum.

Art der Extrempunkte (einfacher)

$\begin{array}{l} f^{'} (0) = 2 (\ln ({(- 1)}^{2}) + 2) = 4 > 0 \\ f^{'} (1) \to 2 (\ln (0^{2}) + 2) = - \infty \end{array}$

Da $0 < 1 - \frac{1}{e} < 1 < 1 + \frac{1}{e}$ liegen die gewählten Punkte um das erste Extremum herum, aber noch vor dem zweiten Extremum.

Da es keine Polstellen gibt, brauchst du dir um die keine Sorgen zu machen.

$\Rightarrow HP (1 - \frac{1}{e} | \frac{4}{e})$

$\begin{array}{l} f^{'} (1) \to 2 (\ln (0^{2}) + 2) = - \infty < 0 \end{array}$

$\Rightarrow TP (1 + \frac{1}{e} | - \frac{4}{e})$

Bestimme das Monotonieverhalten.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten
Eine Funktion kann entweder streng monoton steigen oder fallen.
Das Monotonieverhalten ändert sich an den Minima und Maxima und es kann sich an den Definitionslücken ändern, wenn es Polstellen sind.
In den Intervallen zwischen diesen Punkten ist die Funktion stetig und hat dasselbe Monotonieverhalten.
Man kann alle kritischen Punkte nacheinander abarbeiten.
$x_{Mon}$
$- \infty$
$- 1$
$1 - \frac{1}{e}$
$1$
$1 + \frac{1}{e}$
$\infty$
$\lim_{x \to x_{Mon}} f (x)$
$- \infty$
$- 4 \ln (4)$
$\frac{4}{e}$
$0$
$- \frac{4}{e}$
$\infty$
Zwischen diesen Punkten ist die Funktion jeweils streng monoton. Ob die Funktion fällt oder steigt sieht man an den Grenzwerten.
$x_{Mon}$
$- \infty$
$- 1$
$1 - \frac{1}{e}$
$1$
$1 + \frac{1}{e}$
$\infty$
$\lim_{x \to x_{Mon}} f (x)$
$- \infty$
$- 4 \ln (4)$
$\frac{4}{e}$
$0$
$- \frac{4}{e}$
$\infty$
$↗$
$↗$
$↘$
$↘$
$↗$
steigend
steigend
fallend
fallend
steigend
Diese Beobachtungen kann man noch mit Intervallen angeben.
Die Funktion $f$ ist…
…monoton steigend für $x \in] - \infty; 1 - \frac{1}{e} [∖ {- 1} \cup] 1 + \frac{1}{e}; \infty [$ .
monoton fallend für $x \in] 1 - \frac{1}{e}; 1 + \frac{1}{e} [∖ {1}$ .
Berechne die Wendepunkte.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte
Wendepunkte geben Änderungen der Krümmung des Funktionsgraphen an. Rechtsgekrümmte Graphen verlaufen in einer Rechtskurve, linksgekrümmte Graphen in einer Linkskurve.
Ändert sich dieses Verhalten, dann liegt ein Wendepunkt oder eine Definitionslücke im Kurvenverlauf vor.
Die Krümmung eines Graphen wird durch die 2. Ableitung beschrieben.
Da sich bei einem Wendepunkt die Krümmung ändert ist sie am Punkt selber quasi nicht vorhanden, also 0.
Zur Bestimmung der Lage der Wendepunkte musst du also die 2. Ableitung gleich 0 setzen.
Lage der Wendepunkte
Bisher bekannt sind die Funktion und die 1. Ableitung:
$\begin{array}{l} f (x) = 2 (x - 1) \ln ({(x - 1)}^{2}) \\ f^{'} (x) = 2 (\ln ({(x - 1)}^{2}) + 2) \end{array}$
Für die 2. Ableitung musst du die 1. Ableitung nochmal ableiten.
Diesmal reicht die Anwendung der Kettenregel aus.
$f^{''} (x) = 2 \frac{2 (x - 1)}{{(x - 1)}^{2}} = \frac{4}{x - 1}$
Nun musst du noch die 2. Ableitung gleich 0 setzen.
Da der Zähler aber immer von 0 verschieden ist, wird auch die zweite Ableitung nie 0. Deshalb gibt es keine Wendepunkte.
Bemerkung: Das bedeutet nicht, dass sich die Krümmung nicht ändert. Wie du später sehen wirst ändert sich die Krümmung des Graphen nämlich doch einmal. An dieser Stelle ist nur kein Wendepunkt.
Bestimme das Krümmungsverhalten.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Krümmungsverhalten
Das Krümmungsverhalten ist eine Eigenschaft der Funktion, die angibt, in welche Richtung sich der Graph bewegt, bzw. welche Kurve er beschreibt.
Das Krümmungsverhalten ändert sich an allen Wendepunkten und es kann sich an allen Definitionslücken ändern.
Diese Punkte musst du nacheinander betrachten. Dabei kannst du ausnutzen, dass das Krümmungsverhalten sich wie das Monotonieverhalten der Ableitung verhält:
$x_{K r \ddot{u} m m}$
$- \infty$
$- 1$
$1$
$\infty$
$\lim_{x \to x_{K r \ddot{u} m m}} f^{'} (x)$
$\infty$
$2 \ln (4) + 4$
$- \infty$
$\infty$
Steigung von $f^{'}$
$↘$
$↘$
$↗$
Krümmung von $f$
rechtsgekrümmt
rechtsgekrümmt
linksgekrümmt
Du kannst auch mit der 2. Ableitung arbeiten. Dabei setzt du immer einen beliebigen Punkt zwischen den Intervallgrenzen in die 2. Ableitung ein. Ist das Ergebnis positiv, dann ist der Graph der Funktion in dem Intevall, aus dem der Punkt ist linksgekrümmt.
Ist es negativ, dann ist der Graph der Funktion dort rechtsgekrümmt.
Auch hier kann man wieder die Intervalle angeben.
Die Funktion $f$ ist
rechtsgekrümmt für $x \in] - \infty; 1 [∖ {- 1}$ .
linksgekrümmt für $x \in] 1; \infty [$ .
Berechne den Wertebereich.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich
Der Wertebereich oder die Wertemenge einer Funktion ist die Menge aller Zahlenwerte, die die Funktion mindestens einmal annimmt.
Ist die Funktion in einem Intervall stetig, dann ist dort auch der Wertebereich ein Intervall.
Grenzen des Wertebereichs
Die Grenzen des Wertebereichs sind der minimale Wert und der maximale Wert, den die Funktion annimmt.
Diese Werte erhältst du entweder aus den Grenzwerten oder den Extremwerten.
$HP (1 - \frac{1}{e} | \frac{4}{e}) \Rightarrow y_{m a x} = \frac{4}{e}$
$TP (1 + \frac{1}{e} | - \frac{4}{e}) \Rightarrow y_{\min} = - \frac{4}{e}$
Das wären die $y$ -Werte des Minimums und des Maximums. Das sind aber nicht die kleinst- und größtmöglichen Werte, denn…
$\lim_{x \to - \infty} f (x) = - \infty \Rightarrow y_{\min} = - \infty$
$\lim_{x \to \infty} f (x) = \infty \Rightarrow y_{\max} = \infty$
…der Grenzwert im Unendlichen erlaubt Werte im Unendlichen.
Lücken im Wertebereich
Genauso wie es Definitionslücken gibt, können an diesen Unstetigkeitsstellen auch Lücken im Wertebereich auftreten. Die musst du noch überprüfen, um den Wertebereich angeben zu können.
Bei der Grenzwertbetrachtung wurde berechnet:
$\lim_{x \to - 1} f (x) = - 4 \cdot \ln (4)$
Dieser Wert ist vom Wertebereich ausgenommen, wenn er nicht an einer anderen Stelle doch noch angenommen wird. Das musst du noch prüfen.
Da die Funktion von $- \infty$ kommt und das Maximum bei $x = 1 - \frac{1}{e}$ liegt, steigt die Funktion im Bereich um -1.
Im weiteren Funktionsverlauf fällt die Funktion dann nur noch einmal nämlich auf das Minimum $y = - \frac{4}{e}$ das höher liegt als $- 4 \ln (4)$ Also wird dieser Wert nicht mehr angenommen und ist eine Lücke im Wertebereich.
$\lim_{x \to 1} f (x) = 0$
Der Wert 0 wird von der Funktion aber schon noch zweimal angenommen (die beiden Nullstellen) und ist daher keine Lücke im Wertebereich.
$\Rightarrow 𝕎_{f} = ℝ ∖ {- 4 \cdot \ln (4)}$
Zeichne den Graph.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Graphen zeichnen
Wenn du den Funktionsgraphen zeichnen sollst, musst du alle Größen einzeichnen, die du zuvor ausgerechnet hast.
Wenn alles richtig ausgerechnet wurde, dann kannst du auch den Graphen sinnvoll zeichnen.
In dieser Zeichnung sind eingetragen:
Definitionslücken: $A (- 1 | - 4 \cdot \ln (4)), B (1 | 0)$
Nullstellen: ${Nst}_{1} (0 | 0), {Nst}_{2} (2 | 0)$
Extrempunkte: $HP (1 - \frac{1}{e} | \frac{4}{e}), TP (1 + \frac{1}{e} | - \frac{4}{e})$
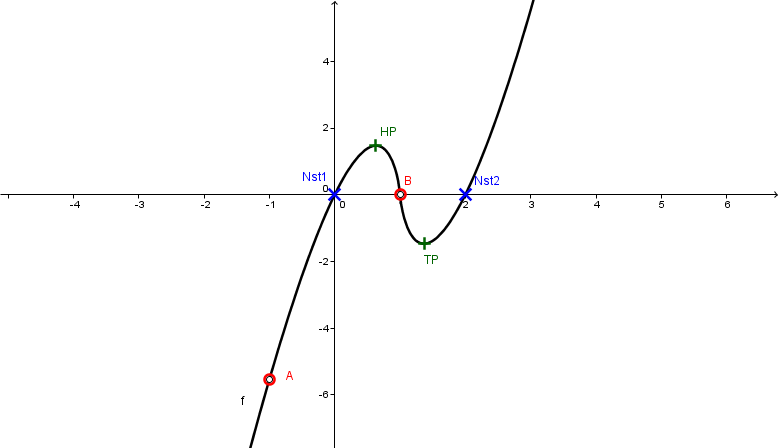
Bemerkungen:
Der nicht vorhandene Wendepunkt würde sich im Punkt $B$ befinden (Der Graph macht davor eine Rechtskurve und danach eine Linkskurve). Der Punkt $B$ ist aber eine Definitionslücke.
Am Punkt $B$ gehört die x-Achse des Koordinatensystems natürlich eigentlich durchgezeichnet. Der weiße Fleck dient zur Verdeutlichung der Definitionslücke.
Auch die Grenzwerte sind hier abzulesen: Richtung $+ \infty$ geht auch der Graph nach $+ \infty$ und Richtung $- \infty$ gegen $- \infty$ .
Überprüfe das Symmetrieverhalten.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrieverhalten
Es gibt zwei Arten von Symmetrie: Achsensymmetrie und Punktsymmetrie
Für einen zu einer Achse $x = c$ achsensymmetrischen Graphen gilt $f (c + x) = f (c - x)$ Gewöhnlich überprüft man nur Achsensymmetrie zur y-Achse mit $x = 0$ , also $f (x) = f (- x)$
Für einen zum Punkt $(c | d)$ punktsymmetrischen Graphen gilt $d - f (c - x) = - d + f (c + x)$ Gewöhnlich überprüft man nur Punktsymmetrie zum Ursprung $(0 | 0)$ , also $- f (x) = f (- x)$
Da man nicht alle Punkte und Achsen überprüft werden können, prüft man nur Ursprung und y-Achse.
Dabei beginnt man mit $f (- x)$ und vergleicht das Aussehen dieser Funktion mit $f (x)$ und $- f (x)$ .
Symmetrie zum Ursprung / zur y-Achse
$\begin{array}{rcl} f (- x) & = & 2 (- x - 1) \cdot \ln ({(- x - 1)}^{2}) \\ = & - 2 (x + 1) \cdot \ln ({(x + 1)}^{2}) \end{array}$
aber
$\begin{array}{rcl} - f (x) & = & - 2 (x - 1) \cdot \ln ({(x - 1)}^{2}) \neq f (- x) \\ f (x) & = & 2 (x - 1) \cdot \ln ({(x - 1)}^{2}) \neq f (- x) \end{array}$
Deshalb keine Symmetrie zu Ursprung oder y-Achse
Symmetrie zum vermuteten Symmetriezentrum
Soll man aber die Symmetrie zu einem gegebenen Punkt überprüfen oder mit dem Funktionsgraphen das Symmetriezentrum bestimmen, dann kann man auch die allgemeine Formel anwenden müssen.
Mit dem groben Bild des Funktionsgraphen aus der vorigen Aufgabe im Hinterkopf, vermutest du, dass der Graph punktsymmetrisch zum Punkt $(1 | 0)$ sein könnte. Das überprüfst du jetzt.
$- f (1 - x) = - 2 (1 - x - 1) \cdot \ln ({(1 - x - 1)}^{2}) = 2 x \cdot \ln (x^{2})$
und
$f (1 + x) = 2 (1 + x - 1) \cdot \ln ({(1 + x - 1)}^{2}) = 2 x \cdot \ln (x^{2})$
Die beiden Ausdrücke sind identisch, was auf Punktsymmetrie zum Punkt $(1 | 0)$ schließen lässt.
Jetzt sind wir aber noch nicht fertig. Sehen wir uns den Graphen nochmal an, dann erkennen wir, dass die linke Seite bei x = -1 eine Lücke im Graphen hat, die die rechte Seite nicht hat. Der Graph deckt sich also bei einer Spiegelung nicht immer auf sich selbst. Deshalb keine Symmetrie!

$x_{Mon}$	$- \infty$	$- 1$	$1 - \frac{1}{e}$	$1$	$1 + \frac{1}{e}$	$\infty$
$\lim_{x \to x_{Mon}} f (x)$	$- \infty$	$- 4 \ln (4)$	$\frac{4}{e}$	$0$	$- \frac{4}{e}$	$\infty$

$x_{Mon}$	$- \infty$		$- 1$		$1 - \frac{1}{e}$		$1$		$1 + \frac{1}{e}$		$\infty$
$\lim_{x \to x_{Mon}} f (x)$	$- \infty$		$- 4 \ln (4)$		$\frac{4}{e}$		$0$		$- \frac{4}{e}$		$\infty$
		$↗$		$↗$		$↘$		$↘$		$↗$
		steigend		steigend		fallend		fallend		steigend

$x_{K r \ddot{u} m m}$	$- \infty$		$- 1$		$1$		$\infty$
$\lim_{x \to x_{K r \ddot{u} m m}} f^{'} (x)$	$\infty$		$2 \ln (4) + 4$		$- \infty$		$\infty$
Steigung von $f^{'}$		$↘$		$↘$		$↗$
Krümmung von $f$		rechtsgekrümmt		rechtsgekrümmt		linksgekrümmt

Bestimme die Tangente zur Funktion $f$ am allgemeinen Punkt $(p | f (p))$ .

Bestimme die Schnittpunkte des Funktionsgraphen $G_{f}$ von $f$ mit dem Funktionsgraphen $G g$ von der Funktion
$g : x \mapsto 2 (x - 1) \cdot \ln (x), 𝔻_{g} = ℝ^{+}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte zweier Funktionsgraphen
Wenn sich zwei Graphen schneiden, dann liefern beide Funktionen an den Schnittpunkten das gleiche Ergebnis. Die Funktionswerte sind an diesen Punkten identisch.
x- Werte bestimmen
Zur Bestimmung der Schnittpunkte reicht es also, die Funktionen gleich zu setzen und nach $x$ aufzulösen, da man dann die $x$ -Werte erhält, für die die Funktionen dasselbe Ergebnis liefern.
Du setzt an:
$\begin{array}{rcl} f (x) & = & g (x) \\ 2 (x - 1) \ln ({(x - 1)}^{2}) & = & 2 (x - 1) \ln (x) \end{array}$
Auf beide Seiten stehen Produkte mit dem gleichen Faktor $2 (x - 1)$ . Falls dieser Faktor nicht 0 ist, darfst du durch ihn dividieren.
Du machst eine Fallunterscheidung:
Fall 1: $2 (x - 1) \neq 0 :$
$\begin{array}{rcll} \ln ({(x - 1)}^{2}) & = & \ln (x) & | e \\ {(x - 1)}^{2} & = & x \\ x^{2} - 2 x + 1 & = & x & | - x \\ x^{2} - 3 x + 1 & = & 0 \end{array}$
Im ersten Fall erhältst du eine quadratische Gleichung, die du nun mit der Mitternachtsformel lösen kannst.
$\begin{array}{ccc} x_{1; 2} & = & \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} \\ = & \frac{3 \pm \sqrt{9 - 4}}{2} \end{array}$
$\Rightarrow x_{1} = \frac{1}{2} (3 + \sqrt{5})$ und $x_{2} = \frac{1}{2} (3 - \sqrt{5})$
Mit der Mitternachtsformel erhältst du die $x$ -Werte von zwei Schnittpunkten.
Nun muss aber noch der 2. Fall betrachtet werden!
Fall 2: $2 (x - 1) = 0$
$\begin{array}{rrcl} 2 (x - 1) & = & 0 \\ \Leftrightarrow & x & = & 1 & \notin 𝔻_{f} \end{array}$
Fall 2 tritt nur ein, wenn $x = 1$ gilt. Da 1 nicht im Definitionsbereich liegt, kann auch dieser Fall nicht eintreten und du bist fertig.
y-Werte bestimmen
Um die Schnittpunkte angeben zu können, muss man sowohl $x$ - als auch $y$ - Werte kennen. Du setzt deshalb die gefundenen $x$ -Werte noch in eine Funktion ein und erhältst die gesuchten $y$ -Werte.
Da du Schnittpunkte berechnest, sind die Funktionswerte bei beiden Funktionen gleich - du wählst also am besten die einfachere.
$\begin{array}{rcl} g (\frac{1}{2} (3 + \sqrt{5})) & = & 2 (\frac{1}{2} (3 + \sqrt{5}) - 1) \ln (\frac{1}{2} (3 + \sqrt{5})) \\ = & (1 + \sqrt{5}) \ln (\frac{1}{2} (3 + \sqrt{5})) \end{array}$
$\begin{array}{rcl} g (\frac{1}{2} (3 - \sqrt{5})) & = & 2 (\frac{1}{2} (3 - \sqrt{5}) - 1) \ln (\frac{1}{2} (3 - \sqrt{5})) \\ = & (1 - \sqrt{5}) \ln (\frac{1}{2} (3 - \sqrt{5})) \end{array}$
Die Ergebnisse sind nicht schön, aber genau und richtig. Du hast also die Schnittpunkte $S_{1}$ und $S_{2}$ bestimmt:
$S_{1} (\frac{1}{2} (3 + \sqrt{5}) | (1 + \sqrt{5}) \ln (\frac{1}{2} (3 + \sqrt{5}))) S_{2} (\frac{1}{2} (3 - \sqrt{5}) | (1 - \sqrt{5}) \ln (\frac{1}{2} (3 - \sqrt{5})))$
Berechne die Stammfunktion.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Um eine Stammfunktion für $f$ zu finden muss man die Funktion $f$ integrieren . Bei komplizierteren Funktionen kann das schwierig werden, aber bei der Integration gibt es Techniken, die es auch erlauben, solche Funktionen zu integrieren, z.B. Substitution und Partielle Integration
$F (x) = \int f (t) d t$
Zuerst stellst du die Gleichung für das Integral auf.
$F (x)$ ist dabei die gesuchte Stammfunktion zu $f$ .
Dann setzt man die Funktion $f$ ein.
Es gibt zwei Wege, um das Integral zu lösen.
Version 1: Partielle Integration
$F (x) = \int 2 (t - 1) \cdot \ln ({(t - 1)}^{2}) d t$
Hier habst du ein Produkt, das sich nicht ohne Weiteres integrieren lässt. Versuch es mit partieller Integration, wobei
$u^{'} (x) = 2 (x - 1) \land v (x) = \ln ((x - 1))$ .
$\begin{array}{rcl} F (t) & = & \int u^{'} (t) v (t) d t \\ = & u (x) v (x) - \int u (t) v^{'} (t) d t \\ = & {(x - 1)}^{2} \ln ({(x - 1)}^{2}) - \int {(t - 1)}^{2} \frac{2 (t - 1)}{{(t - 1)}^{2}} d t \\ = & \dots \end{array}$
Dass $(x - 1)^{2}$ eine mögliche Stammfunktion von $2 (x - 1)$ ist, kann man durch Ableiten der Stammfunktion überprüfen.
Eigentlich wäre $\int 2 (t - 1) d t = x^{2} - 2 x$ , da man aber bei Stammfunktionen Konstanten beliebig addieren kann kommt man auch auf das schönere $x^{2} - 2 x + 1 = (x - 1)^{2}$ .
Im neuen Integral kürzt sich dann einiges weg…
$\begin{array}{cl} = {(x - 1)}^{2} \ln ({(x - 1)}^{2}) - \int 2 (t - 1) d t \\ = {(x - 1)}^{2} \ln ({(x - 1)}^{2}) - {(x - 1)}^{2} + C \\ = {(x - 1)}^{2} \cdot (\ln ({(x - 1)}^{2}) - 1) + C \end{array}$
(mit einer Konstanten $C$ )
…bis auf das bereits bekannte Integral von $2 (x - 1)$ .
Nachdem das letzte Integral bestimmt ist, dürfen wir nicht vergessen, eine Konstante C zu addieren, die möglicherweise vorhanden, aber nicht auffällt, weil sie beim Ableiten sofort wegfällt.
$\Rightarrow F (x) = {(x - 1)}^{2} \cdot (\ln ({(x - 1)}^{2}) - 1) + C$
Wird nur verlangt, dass man eine Stammfunktion angeben soll, dann kann man auch $C = 0$ setzen und die Konstante weglassen.
Version 2: Substitution
$F (x) = \int 2 (t - 1) \cdot \ln ({(t - 1)}^{2}) d t$
Für eine Substitution benötigst du ein Integral der Form
$\int g^{'} (t) f (g (t)) d t$ .
Genau das liegt aber vor. Wir wählen
$f (x) = \ln x$ und $g (x) = (x - 1)^{2} = z$ .
$\begin{array}{ccc} F (x) & = & \int 2 (t - 1) \cdot \ln ({(t - 1)}^{2}) d t \\ F (z) & = & \int \ln (z) d z \\ = & z (\ln (z) - 1) + D \end{array}$
Da du ein unbestimmtes Integral hast, kannst du die Integrationsgrenzen natürlich nicht anpassen.
Die Stammfunktion des Logarithmus solltest du aus der Schule kennen, kurz irgendwo nachschlagen oder aber nochmal mit partieller Integration nachrechnen.
Nun musst du nur noch resubstituieren.
$z = (x - 1)^{2}$
$\Rightarrow F (x) = {(x - 1)}^{2} (\ln ({(x - 1)}^{2}) - 1) + C$
Schon bist du fertig. Das zeigt wieder: Wenn du bestimmte Eigenarten von Funktionen siehst, kannst du dir einiges an Arbeit sparen.
Beachte: Die Stammfunktion ist nur auf stetigen Abschnitten der Ausgangsfunktion $f$ definiert, also nicht auf den Definitionslücken -1 und 1 !
Bestimme die Größe der Fläche zwischen dem Graphen der Funktion $f$ , der x-Achse und den Geraden $x = - 0,5$ und $x = 0,5$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integration
Zur Berechnung der Fläche unter dem Graphen zwischen zwei bestimmten Stellen muss man die Funktion von der linken Grenze bis zur rechten Grenze integrieren. Dabei darf die Funktion zwischen den Grenzen die x-Achse nicht schneiden, da sich sonst die Flächen unter und über der x-Achse wieder gegenseitig wegheben können.
Wenn die Funktion eine Nullstelle im Integrationsintervall hat muss man zuerst bis zur Nullstelle integrieren und dann von der Nullstelle aus weiter, da man nur positive Flächen betrachtet.
$\begin{array}{rcl} A & = & | \int_{- 0,5}^{0,5} | f (x) | d x | \\ = & | \int_{- 0,5}^{0} f (x) d x + \int_{0}^{0,5} f (x) d x | \\ = & | F (0) - F (- 0,5) + F (0,5) - F (0) | \\ = & | - 1 - 0,25 \cdot (\ln (2,25) - 1) + 0,25 \cdot (\ln (0,25) - 1) + 1 | \\ = & | 0,25 (\ln (0,25) - \ln (2,25)) | \\ = & | 0,25 \cdot \ln (\frac{0,25}{2,25}) | \\ = & | 0,25 \cdot \ln (\frac{1}{9}) | \\ \approx & 0,55 \end{array}$
Die Fläche berechnet sich also als der Betrag des Integrals der positiven Funktion von -0,5 bis 0,5.
Spaltet man das Integral an der Nullstelle 0 auf und verwendet die Stammfunktion, dann braucht man nur die Grenzen einzusetzen und zu vereinfachen.
Je nachdem, wie es verlangt wird, kann man das Ergebnis auch als genauen Wert stehen lassen und muss den Logarithmus nicht mehr ausrechnen.
Bestimme die Größe der Fläche die der Graph der stetigen Funktion $\hat{f}$ mit dem Graphen der Tangente von $\hat{f}$ am Punkt $(1 - \frac{1}{e} | \frac{4}{e})$ einschließt.
Hinweis: Runde die Integrationsgrenzen und das Ergebnis auf zwei Nachkommastellen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Integration
Will man die Fläche zwischen zwei Graphen berechnen, so berechnet man zuerst die Fläche unter den "höheren" Graphen und zieht dann die Fläche unter dem "tieferen" Graphen ab.
Da sich die Lage zueinander bei jedem Schnittpunkt ändert muss man zuerst die Schnittpunkte der beiden Graphen kennen:
Schnittpunkte der Graphen
Du kannst hier entweder die Tangentengleichung am Punkt $(1 - \frac{1}{e} | \frac{4}{e})$ aufstellen und damit arbeiten oder du erinnerst dich, dass $(1 - \frac{1}{e} | \frac{4}{e})$ der Hochpunkt von $f$ war.
Deshalb hat die Tangente $t_{HP}$ an diesem Punkt die Steigung 0 und lautet:
$t_{HP} : y = \frac{4}{e}$
Mit diesem Wissen hast du auch schon den ersten Schnittpunkt gefunden Es ist der Hochpunkt $HP (1 - \frac{1}{e} | \frac{4}{e})$ .
Für die anderen Schnittpunkte musst du nun beide Funktionen gleichsetzen:
$\hat{f} (x) = \frac{4}{e}$
Sei $x \neq - 1; 1$
$2 (x - 1) \ln ({(x - 1)}^{2}) = \frac{4}{e}$
Da diese Gleichung nicht exakt lösbar ist, hilft das Newton'sche Näherungsverfahren bei der Funktion
$\tilde{f} (x) = 2 (x - 1) \ln ({(x - 1)}^{2}) - \frac{4}{e}$
Überprüfst du den Funktionsgraphen, dann stellst du fest, dass es nur einen zweiten Schnittpunkt gibt. Dieser liegt zwischen den Werten 2 und 3. Wir wählen $x_{0} = 3$ .
$\begin{array}{ccl} x_{1} & = & x_{0} - \frac{\tilde{f} (x_{0})}{\tilde{f^{'}} (x_{0})} \\ = & 3 - \frac{4 \ln (4) - \frac{4}{e}}{2 (\ln (4) + 2)} \approx 2,40 \end{array}$
Der erste Newtonschritt liefert als neuen Ausgangswert ungefähr 2,40.
Der Wert liegt links von 3 auf der Seite der Nullstelle von $\tilde{f}$ , die ja der Schnittpunkt ist.
Weitere Newtonschritte liefern
$\begin{array}{l} x_{2} = x_{1} - \frac{\tilde{f} (x_{1})}{\tilde{f^{'}} (x_{1})} = 2,32 \\ x_{3} = x_{2} - \frac{\tilde{f} (x_{2})}{\tilde{f^{'}} (x_{2})} = 2,32 \end{array}$
Das Newtonverfahren konvergiert also sehr schnell gegen einen Wert.
Überprüfst du diesen Wert durch Einsetzen in $f$ , erhältst du $f (2,32) \approx 1,47 \approx \frac{4}{e}$ . Das Ergebnis stimmt also im Rahmen der Rechenungenauigkeit.
Das Integral zur Flächenbestimmung geht also von $1 - \frac{1}{e}$ bis $2,32$ .
Flächenberechnung
Die Fläche zwischen zwei Graphen berechnet sich über die Differenz der Flächen unter den einzelnen Integralen.
$\begin{array}{ccc} A & = & \int_{1 - \frac{1}{e}}^{2,32} t_{H P} (x) d x - \int_{1 - \frac{1}{e}}^{2,32} \hat{f} (x) d x \\ = & \int_{1 - \frac{1}{e}}^{2,32} \frac{4}{e} d x - \int_{1 - \frac{1}{e}}^{2,32} 2 (x - 1) \ln ({(x - 1)}^{2}) d x \\ = & {[\frac{4}{e} x]}_{1 - \frac{1}{e}}^{2,32} - F (2,32) + F (1 - \frac{1}{e}) \\ \approx & 3,41 - 0,93 + 0,77 - 0,41 \\ \approx & 2,8 \end{array}$
(Man kann hier auf die Stammfunktion von $f$ zurückgreifen, die dieselbe ist, wie die von $\hat{f}$ , aber überall definiert ist.
Integriert man die Konstante und setzt man die Grenzen ein, so erhält man einen ungefähren Wert für die gesuchte Fläche.)
Berechne den Umfang und den Flächeninhalt des Vierecks ${Nst}_{1} TP {Nst}_{2} HP$
Runde Zwischenergebnisse notfalls auf zwei Nachkommastellen.
Das ist keine typische Analysisaufgabe, sondern eher ein kurzer Abstecher in die Geometrie. Willst du nur Analysis üben, dann kannst du diese Aufgabe gerne ignorieren.
Was wir wissen
Die vier gegebenen Punkte sind die Nullstellen und die Extrema. Ihre Koordinaten lauten
${Nst}_{1} (0 | 0), TP (1 + \frac{1}{e} | - \frac{4}{e}), {Nst}_{2} (2 |; 0), HP (1 - \frac{1}{e} | \frac{4}{e})$ .
Zusätzlich sind die Achsen des Koordinatensystems zueinander senkrecht, was die Bestimmung der Seitenlängen des Vierecks mittels Pythagoras ermöglicht.
Umfang
Bestimme die Längen der Seiten über Pythagoras:
${Nst}_{1} TP = \sqrt{{(1 + \frac{1}{e})}^{2} + {(- \frac{4}{e})}^{2}} \approx 2$
${TPNst}_{2} = \sqrt{{(2 - (1 + \frac{1}{e}))}^{2} + {(- \frac{4}{e})}^{2}} \approx 1,6$
${Nst}_{2} HP = \sqrt{{(2 - (1 - \frac{1}{e}))}^{2} + {(\frac{4}{e})}^{2}} \approx 2$
${HPNst}_{1} = \sqrt{{(1 - \frac{1}{e})}^{2} + {(\frac{4}{e})}^{2}} \approx 1,6$
Du stellst fest, dass jeweils zwei gegenüberliegende Seiten gleich lang sind. Das Vierecks ist also schlimmstenfalls ein Parallelogramm.
Der Umfang lässt sich aber jetzt schon berechnen:
$U_{Viereck} \approx 2 + 1,6 + 2 + 1,6 = 7,2$
Flächeninhalt
Um den Flächeninhalt eines Parallelogramms zu berechnen brauchen wir noch eine Größe, z.B. die Höhe.
Die Höhe zu bestimmen ist aber viel zu umständlich. Für die Flächenberechnung gibt es einfachere Wege:
Methode 1: Analytische Geometrie in der Ebene
Versuche einen Weg über die analytische Geometrie. Für die Fläche eines Paralellogramms gilt im $ℝ^{2}$ :
$A_{▱} = | \det (\vec{AB}; \vec{AD}) |$
mit den aufspannenden Vektoren $\vec{AB}$ und $\vec{AD}$ .
In unserem Fall haben wir die Vektoren
$\vec{AB} = \vec{{Nst}_{1} TP} = (\begin{array}{c} 1 + \frac{1}{e} \\ - \frac{4}{e} \end{array}), \vec{AD} = \vec{{Nst}_{1} HP} = (\begin{array}{c} 1 - \frac{1}{e} \\ \frac{4}{e} \end{array})$
$\begin{array}{ccl} A_{Viereck} & = & | \det (\vec{AB}; \vec{AD}) | \\ = & | \det (\begin{array}{cc} 1 + \frac{1}{e} & 1 - \frac{4}{e} \\ - \frac{4}{e} & \frac{4}{e} \end{array}) | \\ = & | (\begin{array}{c} (1 + \frac{1}{e}) (\frac{4}{e}) - (1 - \frac{1}{e}) (- \frac{4}{e}) \end{array}) | \\ = & | \begin{array}{c} \frac{8}{e} \end{array} | \\ = & \frac{8}{e} \end{array}$
Somit hast du die Fläche des Vierecks berechnet.
Methode 2: Aufspalten in Dreiecke
Siehst du dir den Funktionsgraphen an, kannst du erkennen, dass das gesuchte Viereck durch die x-Achse in zwei Dreiecke aufgeteilt wird. Für die Dreiecksflächen brauchst du nur Grundseite und Höhe. Beides ist durch die Koordinaten gegeben.
Dreieck ${Nst}_{1} {Nst}_{2} HP$ :
Grundseite: Subtrahiere die x-Koordinaten der Nullstellen: $g_{1} = 2 - 0 = 2$
Höhe: Der Betrag der y-Koordinate des Hochpunktes: $h_{1} = \frac{4}{e}$
Dreieck ${Nst}_{1} TP {Nst}_{2}$ :
Grundseite: Subtrahiere die x-Koordinaten der Nullstellen: $g_{2} = 2 - 0 = 2$
Höhe: Der Betrag der y-Koordinate des Tiefpunktes: $h_{2} = \frac{4}{e}$
Fläche des Vierecks ${Nst}_{1} {TPNst}_{2} HP$ :
$A_{▱} = \frac{1}{2} g_{1} h_{1} + \frac{1}{2} g_{2} h_{2} = \frac{1}{2} \cdot 2 \cdot \frac{4}{e} + \frac{1}{2} \cdot 2 \cdot \frac{4}{e} = \frac{8}{e}$
Auch hier ergibt sich - sogar sehr schnell - die Vierecksfläche.

2
Es ist folgende Funktionenschar gegeben:
$f_{k} (x) = e^{- \sqrt{k x}}, k \in ℝ$
In den Teilaufgaben findest du vieles, das du für diese Funktion berechnen kannst.
Suche dir heraus, was du üben möchtest.
Die Teilaufgaben sind in einer logischen Reihenfolge angeordnet, daher wird in späteren Aufgaben auf Ergebnisse von früher zurückgegriffen.
Wenn dir nicht klar ist, woher diese Ergebnisse kommen, dann rechne am besten die zugehörige Teilaufgabe davor nach.
Definitionsbereich bestimmen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich
Hier darf der Wert unter Wurzel nicht negativ werden:
$\begin{array}{l} \sqrt{k x} ist nicht definiert \\ \begin{array}{ccccc} \Leftrightarrow & k x & < & 0 \\ \Leftrightarrow & x & < & 0 & und & k > 0 \\ oder & x & > & 0 & und & k < 0 \end{array} \end{array}$
Hier musst du für den Definitionsbereich eine Fallunterscheidung machen:
Fall 1: $k < 0 \Rightarrow 𝔻_{f} =] - \infty; 0]$
Die positiven Werte von x sind ausgeschlossen.
Fall 2: $k > 0 \Rightarrow 𝔻_{f} = [0; \infty [$
Die negativen Werte sind ausgeschlossen.
Fall 3: $k = 0 \Rightarrow 𝔻_{f} = ℝ$
Die Wurzel ist für alle x gleich 0.

Grenzwertbetrachtungen: Bestimme die Grenzwerte an allen Grenzen des Definitionsbereichs.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwertbetrachtungen
Da es einen Parameter gibt, ist eine Fallunterscheidung nötig.
Fall 1: $k < 0$
$𝔻_{f} =] - \infty; 0]$
$\lim_{x \to 0} e^{- \overset{\to 0}{\overset{⏞}{\sqrt{k x}}}} = 1$
$\lim_{x \to - \infty} \underset{\to 0}{\underset{⏟}{e^{\overset{\to - \infty}{\overset{⏞}{- \overset{\to \infty}{\overset{⏞}{\sqrt{k x}}}}}}}} = 0$
Fall 2: $k > 0$
$𝔻_{f} = [0; \infty [$
$\lim_{x \to 0} e^{- \overset{\to 0}{\overset{⏞}{\sqrt{k x}}}} = 1$
$\lim_{x \to - \infty} \underset{\to 0}{\underset{⏟}{e^{\overset{\to - \infty}{\overset{⏞}{- \overset{\to \infty}{\overset{⏞}{\sqrt{k x}}}}}}}} = 0$
Fall 3: $k = 0$
$𝔻_{f} = (- \infty; \infty)$
$\lim_{x \to - \infty} e^{- \sqrt{kx}} = \lim_{x \to - \infty} e^{- 0} = 1$
$\lim_{x \to \infty} e^{- \sqrt{kx}} = 1$

Asymptoten bestimmen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Asymptoten bestimmen
Waagerechte Asymptoten
Fall 1: $k < 0$
$\lim_{x \to - \infty} f_{k} (x) = 0$
Eine waagerechte Asymptote ist $y = 0$ .
Fall 2: $k > 0$
$\lim_{x \to \infty} f_{k} (x) = 0$
Eine waagerechte Asymptote ist $y = 0$ .
Fall 3: $k = 0$
$f_{0} (x) = e^{- \sqrt{0 \cdot x}} = e^{0} = 1$
Die Grenzwerte existieren zwar (siehe Teilaufgabe b), aber es gibt keine Asymptote, da die Funktion überall den Funktionswert 1 hat und sich ihm nicht bloß annähert.
Senkrechte Asymptoten
Senkrechte Asymptoten gibt es an den Stellen der Definitionslücken. Solche gibt es hier nicht.

Nullstellen bestimmen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktion
Die e-Funktion $e^{x}$ hat die Wertemenge $W = ℝ^{+}$ , das heißt, sie ist im ganzen Definitionsbereich positv und schneidet nie die x-Achse. Da die Funktion $f_{k}$ keine Verschiebung der e-Funktion nach oben oder unten bewirkt, hat sie ebenfalls keine Nullstellen.

Symmetrieverhalten überprüfen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie
Fälle 1 und 2: $k \neq 0$
Die Funktion ist hier nur auf jeweils einer Hälfte der x-Achse definiert. Deshalb kann sie nicht symmetrisch zur y-Achse oder zum Urpsrung sein.
Fall 3: $k = 0$
$f_{0} (x) = e^{- 0} = 1 = f_{0} (- x)$
$\Rightarrow f_{0}$ ist achsensymmetrisch zur y-Achse.
Bemerkung: Für $k = 0$ gilt auch Punktsymmetrie zum Punkt $(0 | 1)$ , aber das nur zur Information

Monotonieverhalten bestimmen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Monotonieverhalten bestimmen
1. Ableitung
Für $k \neq 0$ :
${f_{k}}^{'} (x) = e^{- \sqrt{k x}} \cdot \frac{- 1}{2 \sqrt{k x}} \cdot k$
Dabei haben wir ist die Kettenregel verwendet.
Für $k = 0$ gilt:
$f_{0} (x) = 1 \Rightarrow f_{0}^{'} (x) = 0$
$f$ ist konstant, also ist $f^{'}$ gleich null.
Monotonieverhalten
Fall 1: $k < 0$
Hier müssen wir beachten, dass der Definitionsbereich nur negative $x$ -Werte enthält.
${f_{k}}^{'} (x) = \underset{> 0}{\underset{⏟}{e^{- \sqrt{k x}}}} \cdot \underset{< 0}{\underset{⏟}{\frac{- 1}{2 \underset{> 0}{\underset{⏟}{\sqrt{k x}}}}}} \cdot \underset{< 0}{\underset{⏟}{k}} > 0$
Also ist für $k < 0$ $f_{k}$ streng monoton wachsend.
Fall 2: $k > 0$
Hier liegen nur positive $x$ -Werte im Definitionsbereich.
${f_{k}}^{'} (x) = - \frac{1}{2} \underset{> 0}{\underset{⏟}{e^{- \sqrt{k x}}}} \cdot \underset{> 0}{\underset{⏟}{\frac{k}{\sqrt{k x}}}} < 0$
Also ist für $k > 0$ $f_{k}$ streng monoton fallend.
Fall 3: $k = 0$
$f_{0}^{'} (x) = 0$
Für $k = 0$ ist $f_{k}$ konstant und somit sowohl monoton fallend als auch wachsend.

Krümmungsverhalten bestimmen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Krümmungsverhalten bestimmen
2. Ableitung
${f_{k}}^{'} (x) = {\begin{array}{lcc} - \frac{1}{2} e^{- \sqrt{k x}} \cdot \frac{k}{\sqrt{k x}} & für & k \neq 0 \\ 0 & für & k = 0 \end{array}$
Hier ist für die 2. Ableitung die Quotientenregel und die Kettenregel nötig.
Für $k \neq 0$ gilt:
$\begin{aligned} {f_{k}}^{''} (x) & = - \frac{k}{2} \cdot \frac{\sqrt{k x} \cdot e^{- \sqrt{k x}} \cdot \frac{- k}{2 \sqrt{k x}} - e^{- \sqrt{k x}} \cdot \frac{k}{2 \sqrt{k x}}}{k x} \\ = - \frac{k}{2} \cdot \frac{e^{- \sqrt{k x}} \cdot (\frac{- k}{2} - \frac{k}{2 \sqrt{k x}})}{k x} \\ = \frac{k \cdot e^{- \sqrt{k x}} \cdot (1 + \frac{1}{\sqrt{k x}})}{4 x} \end{aligned}$
Krümmungsverhalten
Fall 1: $k < 0$
${f_{k}}^{''} (x) = \frac{\overset{< 0}{\overset{⏞}{k}} \cdot \overset{> 0}{\overset{⏞}{e^{- \sqrt{k x}} \cdot (1 + \frac{1}{\sqrt{k x}})}}}{\underset{< 0}{\underset{⏟}{4 x}}} > 0$
Für $k < 0$ ist $f_{k}$ linksgekrümmt.
Fall 2: $k > 0$
${f_{k}}^{''} (x) = \frac{\overset{> 0}{\overset{⏞}{k}} \cdot \overset{> 0}{\overset{⏞}{e^{- \sqrt{k x}} \cdot (1 + \frac{1}{\sqrt{k x}})}}}{\underset{> 0}{\underset{⏟}{4 x}}} > 0$
Für $k > 0$ ist $f_{k}$ linksgekrümmt.
Fall 3: $k = 0$
$f_{0}^{'} (x) = 0 \Rightarrow f_{0}^{''} (x) = 0$
Für $k = 0$ ist $f_{k}$ nicht gekrümmt.

Extremwerte bestimmen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwerte bestimmen
Nullstellen der ersten Ableitung
$\begin{array}{ll} {f_{k}}^{'} (x) = 0 & für k = 0 \end{array}$
Die erste Ableitung ist für alle $k \neq 0$ ungleich 0.
Für $k = 0$ aber ist die Ableitung konstant.
Deshalb gibt es keine lokalen Extrema.
Funktionswerte an den Grenzen des Definitionsbereichs
$f_{k} (0) = e^{- \sqrt{0}} = 1 = \max {f_{k} (x)}$
An eingeschlossenen Definitionsgrenzen kann eine Funktion auch ein lokales Maximum oder Minimum annehmen. Das ist hier der Fall. Deshalb gibt es einen Hochpunkt, obwohl der Funktionsgraph streng monoton steigt/fällt.
$\Rightarrow$ HP $(0 | 1)$ für $k \neq 0$
kein Extremum für $k = 0$

Wertebereich bestimmen

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wertebereich bestimmen
Was du weißt:
$\begin{array}{ll} \max {f_{k} (x)} = 1 \\ \lim_{x \to \infty} f_{k} (x) = 0 & für k > 0 \\ \lim_{x \to - \infty} f_{k} (x) = 0 & für k < 0 \\ f_{0} (x) = 1 \end{array}$
Aus den Informationen kannst du ablesen, das sich die Funktion zwischen 0 und 1 bewegt. Die 1 wird angenommen, die 0 nicht.
$\Rightarrow$ keine Nullstellen
$\begin{array}{lll} \Rightarrow & 𝕎_{f} = {\begin{array}{lc} (0; 1] & für & k \neq 0 \\ {1} & für & k = 0 \end{array} \end{array}$
Bemerkung: Die Menge ${1}$ enthält als einzigen Punkt die 1; sie ist kein Intervall. Aber konstante Funktionen nehmen eben nur einen $y$ -Wert an.

Tangente bestimmen:
Bestimme die Tangente an den Funktionsgraphen von $f_{k} (x)$ , die für $k < 0$ auch durch den Punkt $P_{1} (- 1 | 0)$ geht und für $k > 0$ durch den Punkt $P_{2} (1 | 0)$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente bestimmen
1. Tangente: $k < 0$
$T_{1} : x \mapsto m_{1} x + t_{1}$
Den gegebenen Punkt $P_{1}$ kannst du einsetzen.
$0 = - m_{1} + t_{1}$
Außerdem gilt für den Berührpunkt $(x_{0} | f_{k} (x_{0}))$ an der Funktion:
$f_{k} (x_{0}) = {f_{k}}^{'} (x_{0}) x_{0} + t_{1}$
Löse dann nach dem Einsetzen nach $x_{0}$ auf, um den Berührpunkt zu erhalten.
$e^{- \sqrt{k x_{0}}}$ $=$ $\frac{- k \cdot e^{- \sqrt{k x_{0}}}}{2 \sqrt{k x_{0}}} \cdot x_{0} + t_{1}$
$e^{- \sqrt{k x_{0}}}$ $=$ $\frac{- k \cdot e^{- \sqrt{k x_{0}}}}{2 \sqrt{k x_{0}}} \cdot x_{0} + \frac{- k \cdot e^{- \sqrt{k x_{0}}}}{2 \sqrt{k x_{0}}}$ $: (\frac{- k \cdot e^{- \sqrt{k x_{0}}}}{2 \sqrt{k x_{0}}})$
$\frac{2 \sqrt{k x_{0}}}{- k}$ $=$ $x_{0} + 1$ $^{2}$
$\frac{4 k x_{0}}{k^{2}}$ $=$ $x_{0}^{2} + 2 x_{0} + 1$ $\cdot k^{2}$
$0$ $=$ $k^{2} x_{0}^{2} + (2 k^{2} - 4 k) x_{0} + k^{2}$
Hier kannst du jetzt die Mitternachtsformel anwenden:
$\begin{array}{rcl} x_{0_{1; 2}} & = & \frac{- (2 k^{2} - 4 k) \pm \sqrt{{(2 k^{2} - 4 k)}^{2} - 4 k^{4}}}{2 k^{2}} \\ = & \frac{4 k - 2 k^{2} \pm \sqrt{4 k^{4} - 16 k^{3} + 16 k^{2} - 4 k^{4}}}{2 k^{2}} \\ = & \frac{4 k - 2 k^{2} \pm 4 k \sqrt{- k + 1}}{2 k^{2}} \\ = & \frac{1}{k} (2 - k \pm 2 \sqrt{1 - k}) \end{array}$
Betrachte jetzt die Klammer.
Die Funktion ist linksgekrümmt. Es kann daher nur einen Berührpunkt geben.
Der liegt auch näher an der 0 als die Nullstelle der Tangente, weil auch die Tangente streng monoton wächst.
Du nimmst also das Minuszeichen, um weiterzurechnen (beachte, dass hier $k < 0$ ist).
$x_{0} = \frac{1}{k} (2 - k - 2 \sqrt{1 - k})$
Für dieses $x_{0}$ erhältst du nun die Steigung und mit der obigen Gleichung den y-Achsenabschnitt.
${f_{k}}^{'} (x_{0}) = \frac{- k \cdot e^{- \sqrt{2 - k - 2 \sqrt{1 - k}}}}{2 \sqrt{2 - k - 2 \sqrt{1 - k}}} = m_{1} = t_{1}$
Du erhältst als Tangentengleichung
$\Rightarrow y = \frac{- k \cdot e^{- \sqrt{2 - k - 2 \sqrt{1 - k}}}}{2 \sqrt{2 - k - 2 \sqrt{1 - k}}} x - \frac{k \cdot e^{- \sqrt{2 - k - 2 \sqrt{1 - k}}}}{2 \sqrt{2 - k - 2 \sqrt{1 - k}}}$
2. Tangente: k > 0
Hier kannst du die Tangente auch wieder normal ausrechnen.
Es fällt jetzt aber leichter, da du nur dieselben Schritte erneut ausführen musst und sich dabei nur Vorzeichen umdrehen, da jetzt mit $P_{2}$ eingesetzt $t_{2} = - m_{2}$ gilt.
Du erhältst schließlich $T_{2} :$
$\Rightarrow y = \frac{- k \cdot e^{- \sqrt{2 + k - 2 \sqrt{1 + k}}}}{2 \sqrt{2 + k - 2 \sqrt{1 + k}}} x + \frac{k \cdot e^{- \sqrt{2 + k - 2 \sqrt{1 + k}}}}{2 \sqrt{2 + k - 2 \sqrt{1 + k}}}$

Stammfunktion I:
Zeige, dass
$F_{k} (x) = - \frac{2 \cdot e^{- \sqrt{k x}} (\sqrt{k x} + 1)}{k}$
eine Stammfunktion von $f_{k} (x)$ für $k \neq 0$ ist.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Um eine Stammfunktion zu finden, musst du eigentlich integrieren.
Hast du aber eine Funktion gegeben von der du nur zeigen musst, dass sie eine Stammfunktion ist, dann reicht es diese Funktion abzuleiten. Siehe dazu den Hauptsatz der Differential- und Integralrechnung .
$\begin{array}{ccc} F_{k} (x) & = & - \frac{2 \cdot e^{- \sqrt{k x}} (\sqrt{kx} + 1)}{k} \\ {F_{k}}^{'} (x) & = & - \frac{2}{k} \cdot [e^{- \sqrt{k x}} (\sqrt{k x} + 1) \cdot \frac{k}{- 2 \sqrt{k x}} + e^{- \sqrt{k x}} (\frac{k}{2 \sqrt{k x}})] \end{array}$
$\begin{array}{ccl} {F_{k}}^{'} (x) & = & - \frac{2}{k} \cdot e^{- \sqrt{k x}} (\frac{k (\sqrt{k x} + 1)}{- 2 \sqrt{k x}} + \frac{k}{2 \sqrt{k x}}) \\ = & e^{- \sqrt{k x}} (\frac{(\sqrt{k x} + 1)}{\sqrt{k x}} - \frac{1}{\sqrt{k x}}) \\ = & e^{- \sqrt{k x}} (\frac{\sqrt{k x}}{\sqrt{k x}}) \\ = & e^{- \sqrt{k x}} \end{array}$
Mit Hilfe der Produktregel und ein bisschen umformen erhältst du die Lösung:
Die Ableitung ist die Funktion $f$ und damit ist $F$ auch eine Stammfunktion.

Stammfunktion II:
Bestimme durch Rechnung die Stammfunktion von $f_{k}$ .

Achtung, diese Integration ist etwas schwieriger und erfordert mehr Überlegungen und Rechenschritte, als in der Schule normalerweise verlangt werden. Wer allerdings ein paar Tricks beim Integrieren ausprobieren/lernen will kann die Aufgabe gerne bearbeiten oder sich die Lösung anschauen.
Für alle Anderen reicht es, die Aufgabe "Stammfunktion I" zu bearbeiten, die normalem Schulniveau entspricht.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion berechnen
Es gilt, das Integral $\int e^{- \sqrt{k x}} d x$ zu bestimmen. Dafür sind einige Schritte nötig.
1. Substitution
Du substituierst:
$\begin{array}{ll} u = - \sqrt{k x} \\ \Rightarrow \frac{d u}{d x} = \frac{- k}{2 \sqrt{kx}} = \frac{k}{2 u} \\ \Rightarrow d x = \frac{2 u}{k} d u & für k \neq 0 \end{array}$
Du nutzt hier aus, dass sich die Wurzel beim Ableiten reproduziert, also als Funktion wieder auftaucht.
Der Ausdruck $\frac{d u}{d x}$ beschreibt die Ableitung von $u$ nach $x$ .
Ersetze die Ausdrücke im Integral.
$F_{k} (u) = \int e^{u} \frac{2}{k} u d u$
Das sieht schon schöner aus. Jetzt kannst du integrieren.
2. Partielle Integration
Du integrierst partiell mit: $\begin{array}{l} v (u) = e^{u}, v^{'} (u) = e^{u} \\ w (u) = u, w^{'} (u) = 1 \end{array}$
$\begin{array}{l} \int e^{u} \frac{2}{k} u d u = \frac{2}{k} \int e^{u} u d u = \\ = \frac{2}{k} (e^{u} u - \int e^{u} d u) = \frac{2}{k} (e^{u} u - e^{u}) \\ = \frac{2 e^{u} (u - 1)}{k} \end{array}$
Jetzt ist das Integralzeichen weg. Du bist fast am Ziel.
3. Resubstitution
Nun musst du nur noch resubstituieren…
$\frac{2 e^{u} (u - 1)}{k} = \frac{2 e^{- \sqrt{k x}} (- \sqrt{k x} - 1)}{k} = - \frac{2 e^{- \sqrt{k x}} (\sqrt{k x} + 1)}{k}$
…und bist fertig.
$\Rightarrow F_{k} (x) = - \frac{2 e^{- \sqrt{k x}} (\sqrt{k x} + 1)}{k} + C$

Flächenberechnung I:
Berechne die Fläche, die der Funktionsgraph mit den Koordinatenachsen einschließt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung
Erster Fall: $k < 0$
Die Funktion ist auf $(- \infty; 0]$ definiert und positiv.
$\begin{array}{ll} \int_{- \infty}^{0} f (x) d x & = \int_{- \infty}^{0} e^{- \sqrt{k x}} d x \\ = F (0) - \lim_{x \to - \infty} F (x) \\ = - \frac{2 e^{0} (0 + 1)}{k} - \lim_{x \to - \infty} - \frac{2 \overset{0}{\overset{⏞}{e^{- \sqrt{k x}}}} \overset{\infty}{\overset{⏞}{(\sqrt{k x} + 1)}}}{k} \\ = - \frac{2}{k} - 0 \\ = - \frac{2}{k} \end{array}$
Der Grenzwert ist 0, da die $e$ -Funktion schneller steigt und fällt, als jedes Polynom.
Zweiter Fall: $k > 0$
$\begin{array}{ll} \int_{0}^{\infty} f (x) d x & = \int_{0}^{\infty} e^{- \sqrt{k x}} d x \\ = \lim_{x \to \infty} F (x) - F (0) \\ = \lim_{x \to \infty} - \frac{2 \overset{0}{\overset{⏞}{e^{- \sqrt{k x}}}} \overset{\infty}{\overset{⏞}{(\sqrt{k x} + 1)}}}{k} + \frac{2 e^{0} (0 + 1)}{k} \\ = 0 + \frac{2}{k} \\ = \frac{2}{k} \end{array}$
Der Grenzwert ist 0, da die $e$ -Funktion schneller steigt und fällt, als jedes Polynom.
Dritter Fall: $k = 0$
Für $k = 0$ ist die Funktion konstant 1.
$\int_{- \infty}^{\infty} f (x) d x = \int_{- \infty}^{\infty} 1 d x = \infty$

Flächenberechnung II:
Berechne die Fläche die von der x-Achse, den Geraden $x = - 1, x = 1$ und dem Graphen von $f_{1} (| x |)$ eingeschlossen wird.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung
Die Funktion $f_{1} (| x |)$ ist achsensymmetrisch zur y-Achse und zusammengesetzt für $x < 0$ aus $f_{- 1} (x)$ und für $x > 0$ aus $f_{1} (x)$ .
Überlege dir das am besten anhand einer Skizze
$\begin{array}{ll} \int_{- 1}^{1} & f_{1} (| x |) d x = \int_{- 1}^{0} f_{- 1} (x) d x + \int_{0}^{1} f_{1} (x) d x \\ = F_{- 1} (0) - F_{- 1} (- 1) + F_{1} (1) - F_{1} (0) \\ = 2 e^{- \sqrt{- 0}} (\sqrt{- 0} + 1) - 2 e^{- \sqrt{1}} (\sqrt{1} + 1) - 2 e^{- \sqrt{1}} (\sqrt{1} + 1) + 2 e^{- \sqrt{0}} (\sqrt{0} + 1) \\ = 2 - \frac{4}{e} - \frac{4}{e} + 2 \\ = 4 (1 - \frac{2}{e}) \end{array}$

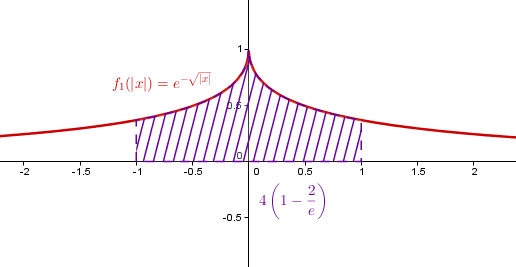
Graphen zeichnen:
Zeichne folgende Graphen für $k = \pm 3$ in ein oder mehrere Koordinatensysteme:
$G_{f}$ mit seinen Asymptoten $G_{f^{'}}, G_{F}$ und $G_{T}$

Graphen zeichnen
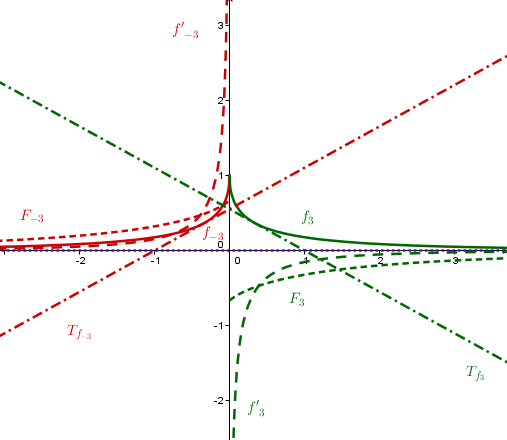
Bemerkungen:
Die Funktionsgraphen sind mit durchgezogenen Linien eingezeichnet,
die Ableitungen mit lang gestrichelten Linien,
die Stammfunktionen mit kurz gestrichelten Linien,
die Tangenten mit abwechselnd Punkten und Strichen,
und die Asymptote ist lila gepunktet.

Es ist folgende Funktion gegeben:

f (x) = \frac{x + 1}{x^{2} - 4}

In den folgenden Teilaufgaben werden verschiedene Teile einer Kurvendiskussion abgefragt.

Suche dir das heraus, was du üben möchtest.

Bei späteren Teilaufgaben kann auf frühere Ergebnisse zurückgegriffen werden.

Ist dir nicht sofort klar, woher diese Ergebnisse kommen, dann bearbeite zunächst diese früheren Teilaufgaben zur Wissensauffrischung.

Bestimme den maximalen Definitionsbereich der Funktion.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
$f (x)$ $=$ $\frac{x + 1}{x^{2} - 4}$
↓
Berechne die Nullstellen des Nenners.
$x^{2} - 4$ $=$ $0$
$x^{2}$ $=$ $4$
↓
Die Nullstellen des Nenners sind die Definitionslücken der Funktion.
$x_{1}$ $=$ $- 2$
$x_{2}$ $=$ $2$
Der maximale Definitionsbereich ist
$ℝ \ {- 2,2}$
Bestimme die Schnittpunkte mit den Koordinatenachsen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Schnittpunkt mit der y-Achse:
$f (x)$ $=$ $\frac{x + 1}{x^{2} - 4}$
↓
Setze 0 in die Funktion ein.
$f (0)$ $=$ $\frac{0 + 1}{0^{2} - 4}$
$f (0)$ $=$ $- \frac{1}{4}$
Der Schnittpunkt mit der y-Achse befindet sich bei $(0 | - \frac{1}{4})$
Schnittpunkt mit der x-Achse (Nullstelle):
$f (x)$ $=$ $\frac{x + 1}{x^{2} - 4}$
↓
Berechne die Nullstelle des Zählers.

$x + 1$ $=$ $0_{}$
$x$ $=$ $- 1$
Der Schnittpunkt mit der x-Achse befindet sich bei $(- 1 | 0)$
Gib die Asymptoten der Funktion an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Senkrechte Asymptoten:
$f (x) = \frac{x + 1}{x^{2} - 4}$
Die Definitionslücken sind senkrechte Asymptoten.
Es gibt zwei senkrechte Asymptoten bei
$x = - 2$
und
$x = 2$
Waagrechte oder schräge Asymptote:
$f (x) = \frac{x + 1}{x^{2} - 4}$
Vergleiche Zähler- und Nennergrad.
Hier ist der Nennergrad größer als der Zählergrad, deswegen gibt es eine waagrechte Asymptote bei
$y = 0$
Überprüfe die Funktion auf Achsensymmetrie bezüglich der y-Achse und Punktsymmetrie zum Ursprung.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Achsensymmetrie zur y-Achse:
$f (x) = \frac{x + 1}{x^{2} - 4}$
Bei Achsensymmetrie muss die Formel
$f (x) = f (- x)$
gelten. Berechne
$f (- x)$
$f (- x) = \frac{- x + 1}{(- x)^{2} - 4} = \frac{- x + 1}{x^{2} - 4}$
Die Formel gilt hier also nicht, das heißt die Funktion ist nicht achsensymmetrisch zur y-Achse.
Punktsymmetrie zum Ursprung:
$f (x) = \frac{x + 1}{x^{2} - 4}$
Bei Punktsymmetrie zum Ursprung muss folgende Formel gelten
$f (- x) = - f (x)$
Berechne
$- f (x)$
$- f (x) = - \frac{x + 1}{x^{2} - 4}$
Die Formel gilt also nicht, das heißt die Funktion ist nicht punktsymmetrisch zum Ursprung.
Die Funktion ist weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung.

Bestimme die Tangente an die Funktion an der Stelle

x = 0

Hat die Funktion Extremstellen? Bestimme sie gegebenenfalls.

4
Im Labor wird eine Maispflanze beobachtet, um den Wachstumsverlauf zu erforschen. Dazu beginnen die Forscher ihre Aufzeichnungen mit einem Setzling zum Zeitpunkt t=0 und messen die Höhe der Pflanze kontinuierlich über die nächsten sieben Monate.
Die folgende Funktion $h (t)$ konnten die Forscher dabei aufzeichnen:
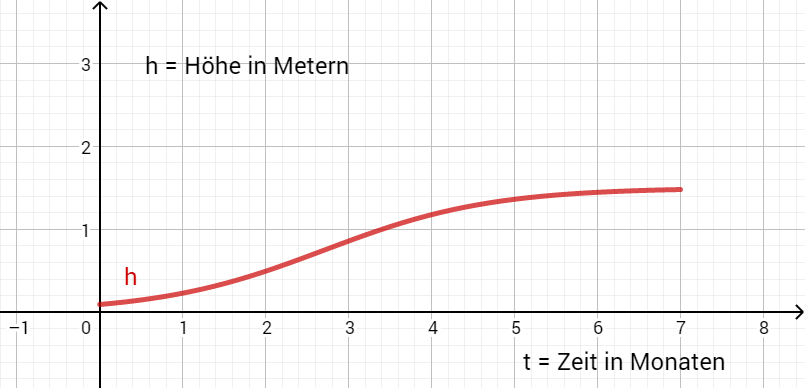
Die Funktion kann modellhaft durch die Funktion $h (t) = \frac{1,5 e^{t}}{e^{t} + 15}$ beschrieben werden.
Dabei ist $t$ die Zeit in Monaten, die seit Beobachtungsbeginn vergangen ist.
$h (t)$ ist die Höhe zur Zeit $t$ in Metern, die die Maispflanze groß ist.
Berechne die Größe in Zentimeter des Setzlings zu Beginn der Beobachtung!

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Berechnung der Anfangshöhe des Setzlings
Um die Höhe des Setzlings zum Anfangszeitpunkt herauszufinden musst du den Funktionswert der Funktion $h (t)$ zum Zeitpunkt $t = 0$ berechnen.
Setze dazu $t = 0$ in $h (t)$ ein.
$h (t = 0) = \frac{1,5 e^{0}}{e^{0} + 15}$
Berechne diesen Wert anschließend.
$h (t = 0) = \frac{1,5 \cdot 1}{1 + 15} = \frac{1,5}{16} = 0,09375 \approx 0,094 [m]$
Rechne diesen Wert anschließend in Zentimeter um.
$0,094 m = 9,4 c m$
Der Setzling ist zu Anfang der Aufzeichnung $9,4 c m$ hoch.

Berechne, wie viele Zentimeter die Maispflanze in den ersten sechs Wochen nach Aufzeichnungsbeginn gewachsen ist!

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionswert
Wachstum der Pflanze in sechs Wochen
Um das Wachstum der Pflanze in den ersten sechs Wochen (=1,5 Monate) herauszufinden musst du die Differenz der Höhe nach sechs Wochen und der Anfangshöhe bilden.
$h_{Δ 6 Wochen} = h (1,5) - h (0)$
Den Funktionswert der Anfangshöhe hast du bereits in der Aufgabe $a$ berechnet.
$h (0) = 9,4 c m$
Du benötigst nun noch den Funktionswert der Höhe nach sechs Wochen.
$h (6 Wochen) = h (1,5) = \frac{1,5 e^{1,5}}{e^{1,5} + 15} \approx 0,345 [m]$
Rechne diese Höhe in Zentimeter um!
$h (1,5) = 0,35 m = 34,5 c m$
Anschließend kannst du das Wachstum der Pflanze in den ersten sechs Wochen berechnen:
$h_{Δ 6 Wochen} = h (1,5) - h (0) = 34,5 c m - 9,4 c m = 25,1 c m$
Die Pflanze ist $25,1 c m$ innerhalb der ersten sechs Wochen nach Beobachtungsbeginn gewachsen.

Zu welchem Zeitpunkt $t$ ist das Wachstum der Pflanze maximal?
Bestimme die Wachstumsrate zu diesem Zeitpunkt in Zentimeter pro Tag!

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung
Maximale Wachstumsrate
Die Wachstumsrate der Pflanze wird durch die Steigung der Funktion beschrieben. Das bedeutet, du musst die maximale Steigung der Funktion finden.
Die Steigung der Funktion $h (t)$ findest du, indem du nach $t$ ableitest. Nutze dazu die Quotientenregel.
$h^{'} (t) = {(\frac{1,5 e^{t}}{e^{t} + 15})}^{'} = \frac{1,5 e^{t} \cdot (e^{t} + 15) - 1,5 e^{t} \cdot e^{t}}{(e^{t} + 15)^{2}}$
Vereinfache diese Ableitung, indem du $1,5 e^{t}$ im Zähler ausklammerst.
$h^{'} (t) = \frac{1,5 e^{t} \cdot (e^{t} + 15 - e^{t})}{(e^{t} + 15)^{2}} = \frac{1,5 e^{t} \cdot 15}{(e^{t} + 15)^{2}} = \frac{22,5 e^{t}}{(e^{t} + 15)^{2}}$
Jetzt hast du eine Funktion, die die Steigung der Funktion beschreibt. Du willst nun das Maximum dieser Steigung herausfinden. Nutze dazu den Ansatz zur Extremwertbestimmung von Funktionen. Berechne dafür die zweite Ableitung mithilfe der Quotientenregel und der Kettenregel:
$h^{''} (t) = {(\frac{22,5 e^{t}}{(e^{t} + 15)^{2}})}^{'} = \frac{22,5 e^{t} \cdot (e^{t} + 15)^{2} - 22,5 e^{t} \cdot 2 (e^{t} + 15) \cdot e^{t}}{(e^{t} + 15)^{4}}$
Diese Ableitung kannst du wiederum vereinfachen indem du zuerst $22,5 e^{t}$ ausklammerst und die Klammern im Zähler ausrechnest.
$h^{''} (t) = \frac{22,5 e^{t} \cdot ((e^{t} + 15)^{2} - 2 (e^{t} + 15) \cdot e^{t})}{(e^{t} + 15)^{4}}$
$h^{''} (t) = \frac{22,5 e^{t} \cdot (e^{2 t} + 225 + 30 e^{t} - 2 e^{2 t} - 30 e^{t})}{(e^{t} + 15)^{4}}$
$h^{''} (t) = \frac{22,5 e^{t} \cdot (- e^{2 t} + 225)}{(e^{t} + 15)^{4}}$
Einen Extremwert der Steigung erhältst du, indem du die zweite Ableitung gleich Null setzt.
$h^{''} (t) = 0$
In diesem Fall reicht es, den Zähler des Bruchs zu betrachten.
$22,5 e^{t} \cdot (- e^{2 t} + 225) = 0$
Da $e^{t}$ niemals Null wird, reicht es wiederum nur die Klammer zu betrachten.
$\begin{matrix} - e^{2 t} + & 225 & = 0 & | + e^{2 t} \\ 225 & = e^{2 t} & | l n (\dots) \\ l n (225) & = 2 t & | : 2 \\ \frac{l n (225)}{2} & = t \\ t & \approx 2,71 \end{matrix}$
Da dies die einzige Extremstelle ist kannst du dir sicher sein, dass es der gefragte Maximalwert ist. Du erhältst also eine maximale Steigung zum Zeitpunkt $t = 2,71$ .
Das bedeutet: $2,71$ Monate nach Beobachtungsbeginn wächst die Maispflanze am stärksten.
Maximale Wachstumsrate
Um die maximale Wachstumsrate in $\frac{c m}{Tag}$ erhältst du indem du die maximale Steigung $h^{'} (t = 2,71)$ berechnest und anschließend in die gewünschte Einheit umrechnest.
$h^{'} (2,71) = \frac{22,5 e^{2,71}}{(e^{2,71} + 15)^{2}} \approx 0,375 [\frac{m}{M o n a t e}]$
Die Einheit $\frac{m}{M o n a t e}$ erhältst du durch die Ableitung der Zeit. Aus $h (t)$ in $m$ wird also nach Ableitung durch $t$ in $M o n a t e n$ :
$h^{'} (t)$ in $\frac{m}{M o n a t e}$
Diese Einheit muss jetzt in $\frac{c m}{T a g e}$ umgerechnet werden. Schreibe dazu die alte Einheit $\frac{m}{M o n a t e}$ in $c m$ und $T a g e$ um.
Nutze dazu die Umrechnung $30 T a g e = 1 M o n a t$
$\frac{m}{M o n a t e} = \frac{100 c m}{30 T a g e} = \frac{10 c m}{3 T a g e} = \frac{10}{3} \cdot \frac{c m}{T a g}$
Du erhältst also als maximale Wachstumsrate:
$h^{'} (2,71) = 0,375 \frac{m}{M o n a t e} = 0,375 \cdot \frac{10}{3} \frac{c m}{T a g} = 1,25 \frac{c m}{T a g}$
Die Pflanze wächst mit maximal $1,25 \frac{c m}{T a g}$ .

Bestimme die maximal zu erreichende Höhe dieser Maissorte, indem du den Grenzwert von h(x) gegen Unendlich betrachtest.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwert
Maximale Höhe der Maispflanze
Wenn man die Funktion nicht bei $7$ Monaten abbrechen würde, sondern weiterzeichnen, sieht man, dass die Funktion eine Art Plateau erreicht.
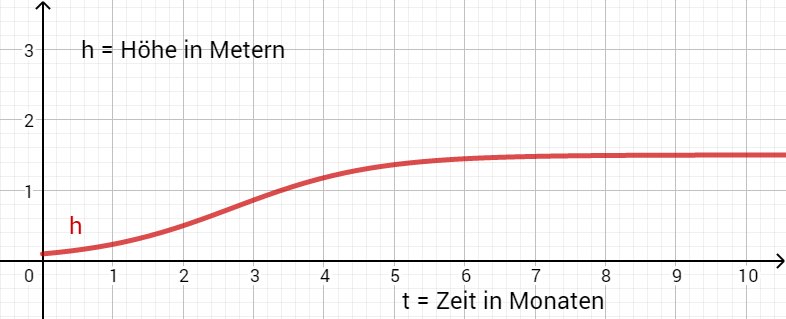
Der Wert dieses Plateaus scheint die maximale Höhe der Pflanze zu sein.
Aus diesem Grund kannst du den Grenzwert der Funktion bestimmen und diesen als maximale Höhe festlegen.
Bestimme dazu den Limes von $h (t)$ gegen unendlich.
$\lim_{t \to \infty} h (t) = \lim_{t \to \infty} \frac{1,5 e^{t}}{e^{t} + 15}$
Den Bruch kannst du aufteilen und die Grenzwerte für den Zähler und Nenner getrennt betrachten:
$\frac{\lim_{t \to \infty} 1,5 e^{t}}{\lim_{t \to \infty} e^{t} + 15}$
Im Nenner spielen die $+ 15$ keine Rolle mehr. Es bleibt übrig:
$\frac{1,5 e^{\infty}}{e^{\infty}} = 1,5 [m]$
Du erhältst nach kürzen einen Grenzwert von $1,5 m$ . Das bedeutet, die maximale Höhe der Pflanze beträgt $1,5 m$ .

Wie müsste die passende Funktionsgleichung $h_{2} (t)$ aussehen, wenn die Pflanze zu Anfang dieselbe Höhe hätte, also $h (0) = h_{2} (0)$ , aber jede weitere Höhe von $h (t)$ exakt in der Hälfte der Zeit von $h_{2} (t)$ erreicht wird ?
$h_{2} (t) = \frac{1,5 e^{k t}}{e^{k t} + 15}$
$h_{2} (t) = \frac{1,5 e^{t}}{e^{t} + 15} \cdot k$
$h_{2} (t) = \frac{1,5 e^{t + k}}{e^{t + k} + 15}$

Betrachte Teilaufgabe $e)$ . Begründe, warum die anderen beiden Antworten nicht richtig sein können!

Begründung der Lösung
Die Lösungen
$I h_{2} (t) = \frac{1,5 e^{t + k}}{e^{t + k} + 15}$
und
$I I h_{2} (t) = \frac{1,5 e^{t}}{e^{t} + 15} \cdot k$
aus Aufgabe $e)$ sind falsch.
Du sollst begründen, warum diese Lösungen nicht den geschilderten Sachkontext erfüllen können.
Betrachte dazu nochmal die Aussage, dass der Anfangswert der ursprünglichen Funktion $h (t)$ auch der Anfangswert der Funktion $h_{2} (t)$ ist. Wichtig ist noch, dass dieser Anfangswert $h (0) = h_{2} (0) \neq 0$ . Das weißt du aus Aufgabe $a)$ oder kannst es aus der Zeichnung auslesen.
Betrachte zunächst $I$ und setze $t = 0$ ein.
$h_{2} (0) = \frac{1,5 e^{0 + k}}{e^{0 + k} + 15} = \frac{1,5 e^{k}}{e^{k} + 15}$
Das sollte nun gleich $h (0)$ sein.
$h (0) = \frac{1,5 e^{0}}{e^{0} + 15} = \frac{1,5}{16}$
Auf dieses Ergebnis kommt man mit $h_{2}$ aber nur, wenn $k = 0$ .
$h_{2} (t) = \frac{1,5 e^{t + 0}}{e^{t + 0} + 15} = \frac{1,5 e^{t}}{e^{t} + 15}$
Somit kann $I$ keine Lösung des Problems sein, da es mit $k = 0$ dieselbe Funktion wie $h (t)$ ist.
Betrachte nun $I I$ und setze $t = 0$ ein.
$h_{2} (0) = \frac{1,5 e^{0}}{e^{0} + 15} \cdot k = h (0) \cdot k$
Für den ersten Teil dieses Terms kann man $h (0)$ einsetzen, da dies genau diesen Bruch ergibt. Da jetzt aber $h_{2} (0) = h (0)$ sein soll, müsste $k$ genau $1$ sein.
Wenn das so ist, erhältst du wie bei $I$ wiederum genau $h_{2} (t) = h (t)$ , was das Problem nicht löst.
Aus diesem Grund muss die dritte Möglichkeit die Lösung des Problems sein.
$h_{2} (t) = \frac{1,5 e^{k t}}{e^{k t} + 15}$
Berechne damit nun die Aufgabe $g)$ !

Betrachte Teilaufgabe $e)$ . Gebe den entsprechenden Wert von $k$ an!

Bestimmung des Koeffizienten
Berechne nun den Koeffizienten $k$ in $h_{2} (t)$ , so dass das in $e)$ beschriebene Problem gelöst wird.
Du weißt bereits, dass die Höhe $h (0) = h_{2} (0)$ ist. Außerdem kennst du den Funktionswert $h (1,5) = 34,5 c m$ aus der Aufgabe $b)$ .
Betrachte nun den Wert $h (1,5)$ und überlege, wann $h_{2} (t)$ diese Höhe erreicht hat.
In der Problemstellung steht, dass $h_{2}$ diesen Wert in der Hälfte der Zeit erreicht. Die Zeit ist in diesem Fall $1,5$ Monate. Die Hälfte ist also somit $0,75$ Monate.
Jetzt kannst du den Funktionsterm aufstellen, da du weißt: $h_{2} (0,75) = h (1,5) = 0,345 m$ .
$h_{2} (0,75) = 0,345 = \frac{1,5 e^{0,75 \cdot k}}{e^{0,75 \cdot k} + 15}$
Diese Gleichung musst du nun nur noch nach dem Koeffizienten $k$ auflösen.
$\begin{matrix} 0,345 & = & \frac{1,5 e^{0,75 \cdot k}}{e^{0,75 \cdot k} + 15} & | \cdot (e^{0,75 \cdot k} + 15) \\ 0,345 \cdot (e^{0,75 k} + 15) & = & 1,5 e^{0,75 k} \\ 0,345 e^{0,75 k} + 5,175 & = & 1,5 e^{0,75 k} & | - 0,345 e^{0,75 k} \\ 5,175 & = & 1,155 e^{0,75 k} & | l n (\dots) \\ l n (5,175) & = & 1,155 \cdot 0,75 k & | : (1,155 \cdot 0,75) \\ \frac{l n (5,175)}{0,86625} & = & k \end{matrix}$
Nach Berechnen mit dem Taschenrechner erhältst du:
$k \approx 1,90$
Damit kannst du nun eine vollständige Funktionsgleichung aufstellen:
$h_{2} (t) = \frac{1,5 e^{1,9 t}}{e^{1,9 t} + 15}$

Die Abbildung zeigt den Graphen der Funktion $g (x) = - \frac{x}{2} \cdot \sqrt{x + 2}$ .

Gib den maximalen Definitionsbereich der Funktion $g$ an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich
Der Definitionsbereich einer Funktion umfasst die Menge der Zahlen, die in die Funktion eingesetzt werden dürfen.
Unter geraden Wurzeln darf kein negativer Radikand stehen, d.h. der Radikand muss größer oder gleich null sein.
Prüfe, wann der Radikand $x + 2$ größer oder gleich null ist.
$x + 2$ $\geq$ $0$ $- 2$
$x$ $\geq$ $- 2$
Damit hat die Funktion $g$ den maximalen Definitionsbereich:

$𝔻_{f} = {x \in ℝ | x \geq - 2}$

Berechne die Nullstellen.

Skaliere in der Abbildung die Koordinatenachsen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
Die in Aufgabe $b$ ) berechneten Nullstellen sind $x_{1} = 0$ und $x_{2} = - 2$ .
Der linke Schnittpunkt mit der $x$ -Achse liegt bei $(- 2 | 0)$ und der rechte Schnittpunkt mit der $x$ -Achse liegt bei $(0 | 0)$ .
In der Abbildung ist der $x$ -Achsenbereich im Intervall $[- 2; 0]$ in $10$ Abschnitte unterteilt. Ein Abschnitt entspricht demnach $0,2$ . Damit kann die $x$ -Achse skaliert werden.
Für die Skalierung der $y$ -Achse berechnest du z.B. den Funktionswert an der Stelle $x = 1$ .
$g (x)$ $=$ $- \frac{x}{2} \cdot \sqrt{x + 2}$
↓
Setze $x = 1$ ein.
$g (1)$ $=$ $- \frac{1}{2} \cdot \sqrt{1 + 2}$
$=$ $= - \frac{1}{2} \cdot \sqrt{3}$
$\approx$ $- 0,87$
Der Punkt $P (1 | - 0,87)$ liegt auf dem Graphen von $g$ und ermöglicht die Skalierung der $y$ -Achse. Die y-Koordinate von $P$ liegt etwas oberhalb von $y = - 1$ .
In der Abbildung ist der $y$ -Achsenbereich im Intervall $[- 1; 0]$ in $5$ Abschnitte unterteilt. Ein Abschnitt entspricht demnach $0,2$ . Damit kann die $y$ -Achse skaliert werden.

Bestimme die Koordinaten des Hochpunktes von g.

Die Untersuchung der notwendigen Bedingung ist ausreichend.

6
$G_{f}$ ist der achsensymmetrische Graph einer Funktion 4. Grades.
Erläutere nur unter Bezugnahme auf Symmetrie und Globalverlauf des Graphen, warum nur Funktionsterm $f_{4}$ infrage kommt.
$\begin{array}{ll} f_{1} (x) & = - 0,1 x^{4} + x^{2} - 0,5 \\ f_{2} (x) & = 0,1 x^{4} + x^{3} - 0,5 \\ f_{3} (x) & = 0,1 x^{3} + x - 0,5 \\ f_{4} (x) & = 0,1 x^{4} - x^{2} - 0,5 \end{array}$

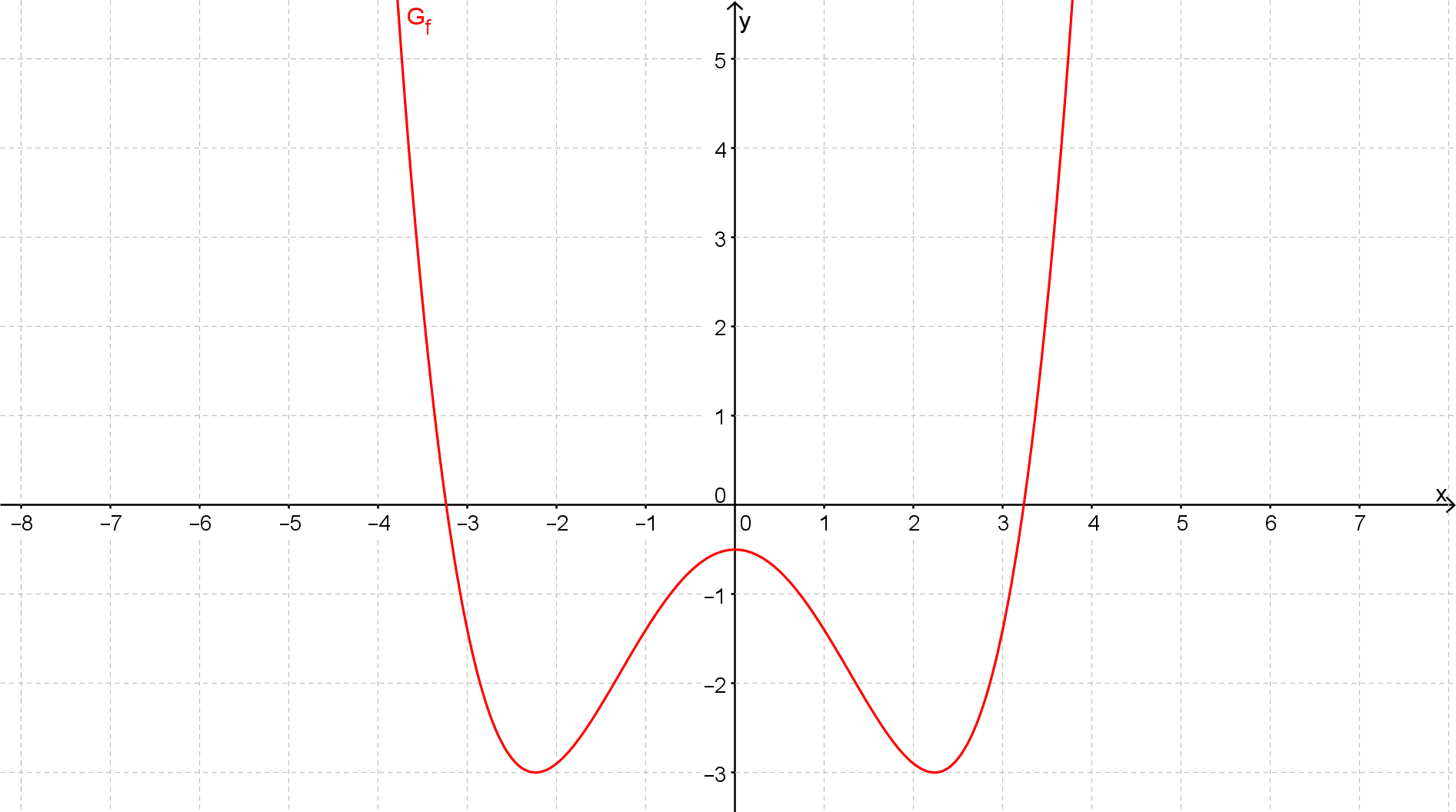
Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwerte bestimmen
Gegenargument gegen Funktion $f_{1}$
$f_{1} (x) = - 0,1 x^{4} + x^{2} - 0,5$ kann nicht der richtige Funktionsterm sein, da aufgrund des negativen Leitkoeffizienten -0,1 und des geraden Grades 4 für den Globalverlauf gilt:
$\lim_{x \mapsto - \infty} f_{1} (x) = - \infty und \lim_{x \mapsto + \infty} f_{1} (x) = - \infty$
Doch im Graph ist $\lim_{x \mapsto - \infty} f (x) = \lim_{x \mapsto + \infty} f (x) = + \infty$ .
Gegenargument gegen Funktion $f_{2}$
Der Graph von $f_{2} (x) = 0,1 x^{4} + x^{3} - 0,5$ ist aufgrund der ungeraden Potenz $x^{3}$ nicht achsensymmetrisch.
Der Graph $G_{f}$ ist aber achsensymmetrisch.
Gegenargument gegen Funktion $f_{3}$
Hier stimmt weder die Symmetrie noch der Globalverlauf!
Da $f_{3} (x) = 0,1 x^{3} + x - 0,5$ einen ungeraden Grad und einen positiven Leitkoeffizienten hat, gilt für den Grenzwert bei $x \mapsto - \infty$ :
$\lim_{x \mapsto - \infty} f_{3} (x) = - \infty$
Außerdem ist die Funktion aufgrund der ungeraden Exponenten nicht achsensymmetrisch.
(Sie ist auch nicht punktsymmetrisch, da sie nicht durch den Ursprung verläuft)
Begründung für Funktion $f_{4}$
Da $f_{4}$ ausschließlich gerade Exponenten hat, ist der zugehörige Graph achsensymmetrisch.
Da der Leitkoeffizient positiv ist und der Grad gerade, hat die Funktion $f_{4}$ auch den gesuchten Globalverlauf.
Überlege dir, wie Leitkoeffizient und Grad der Funktion aussehen müssen, damit der obige Globalverlauf auftritt
Entscheide, ob die Funktion symmetrisch ist und überlege dir, was das für den Funktionsterm bedeutet
7
Graphenzuordnung

Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
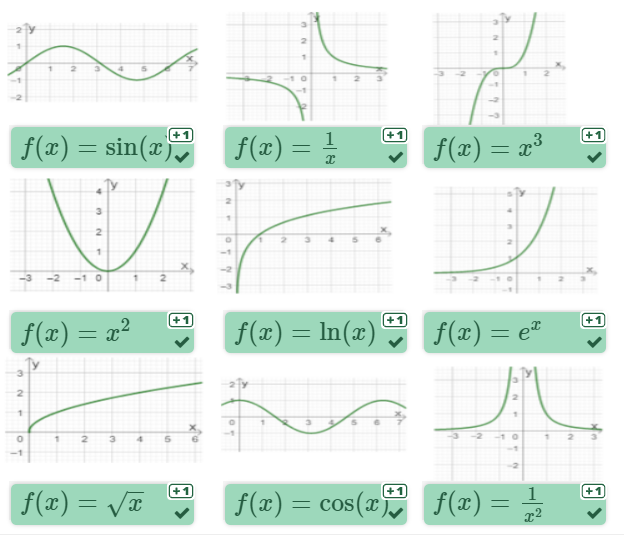
Der Graph gehört zur Sinus-Funktion:
$f (x) = \sin (x)$
Das ist der Graph der Normalparabel:
$f (x) = x^{2}$
Das ist der Graph einer Wurzelfunktion:
$f (x) = \sqrt{x}$
Das ist der Graph einer gebrochen-rationalen Funktion (Hyperbel):
$f (x) = \frac{1}{x}$
Das ist der Graph der ln-Funktion:
$f (x) = \ln (x)$
Der Graph gehört zur Kosinus-Funktion:
$f (x) = \cos (x)$
Das ist der Graph einer Potenzfunktion:
$f (x) = x^{3}$
Das ist der Graph der e-Funktion:
$f (x) = e^{x}$
Das ist der Graph einer gebrochen-rationalen Funktion:
$f (x) = \frac{1}{x^{2}}$
8
Um das Monotonieverhalten (steigend/fallend) und das Krümmungsverhalten (links- oder rechtsgekrümmt) zu untersuchen, kannst du ähnliche Methoden verwenden.
In dieser Aufgabe sollst du dir Gedanken über die Gemeinsamkeiten und Unterschiede machen.
Egal, ob du später eine Skizze oder eine Tabelle anfertigen wirst (oder sogar mit einer höheren Ableitung arbeiten wirst), zunächst musst du Vorarbeit leisten.
Vergleiche, wie du die Kandidaten für Extrem- und Wendestellen bekommst.

Monotonieverhalten
Um die Kandidaten für Extremstellen zu bekommen, musst du:
die 1. Ableitung bilden
die Nullstellen der 1. Ableitung bestimmen
Krümmungsverhalten
Um die Kandidaten für Wendestellen zu bekommen, musst du:
die 2. Ableitung bilden
die Nullstellen der 2. Ableitung bestimmen
Vergleich
Die Gemeinsamkeit: Man leitet ab und man berechnet Nullstellen.
Der Unterschied: Es muss einmal die 1. Ableitung und einmal die 2. Ableitung nullgesetzt werden.
Das Monotonieverhalten wird mithilfe der 1. Ableitung beschrieben
Das Krümmungsverhalten wird mithilfe der 2. Ableitung beschrieben.
Die Nullstellen der beiden Ableitungen liefern die einzigen Kandidaten für die besonderen Graphenpunkte Hochpunkt, Tiefpunkt, Terrassenpunkt und Wendepunkt.

Du untersuchst das Monotonie- und Krümmungsverhalten mithilfe einer Skizze. Wodurch unterscheiden sich die Skizzen zur Monotonie und zur Krümmung?

Monotonieverhalten über Skizze von $G_{f^{'}}$
Du hast zuvor die Nullstellen von $f^{'}$ mit ihren Vielfachheiten berechnet. Gemeinsam mit dem Grad und Leitkoeffizient von $f^{'}$ kannst du den Graphen der Ableitung skizzieren.
Ist der Graph der Ableitung oberhalb der x-Achse, so ist $f^{'} (x) > 0$ und der Graph der Ausgangsfunktion $G_{f}$ steigt streng monoton.
Analog: ist der Graph der Ableitungsfunktion unterhalb der x-Achse, so ist $f^{'} (x) < 0$ und der Graph der Ausgangsfunktion $G_{f}$ fällt streng monoton.
Wechselt der Graph von $f^{'}$ an einer seiner Nullstellen das Vorzeichen, so hat der Graph $G_{f}$ dort eine Extremstelle (Hochpunkt bei sms zu smf, Tiefpunkt bei smf zu sms).
Wechselt der Graph von $f^{'}$ an einer Nullstelle das Vorzeichen nicht (die Nullstelle von $f^{'}$ hat eine gerade Vielfachheit), so hat $G_{f}$ dort einen Terrassenpunkt.
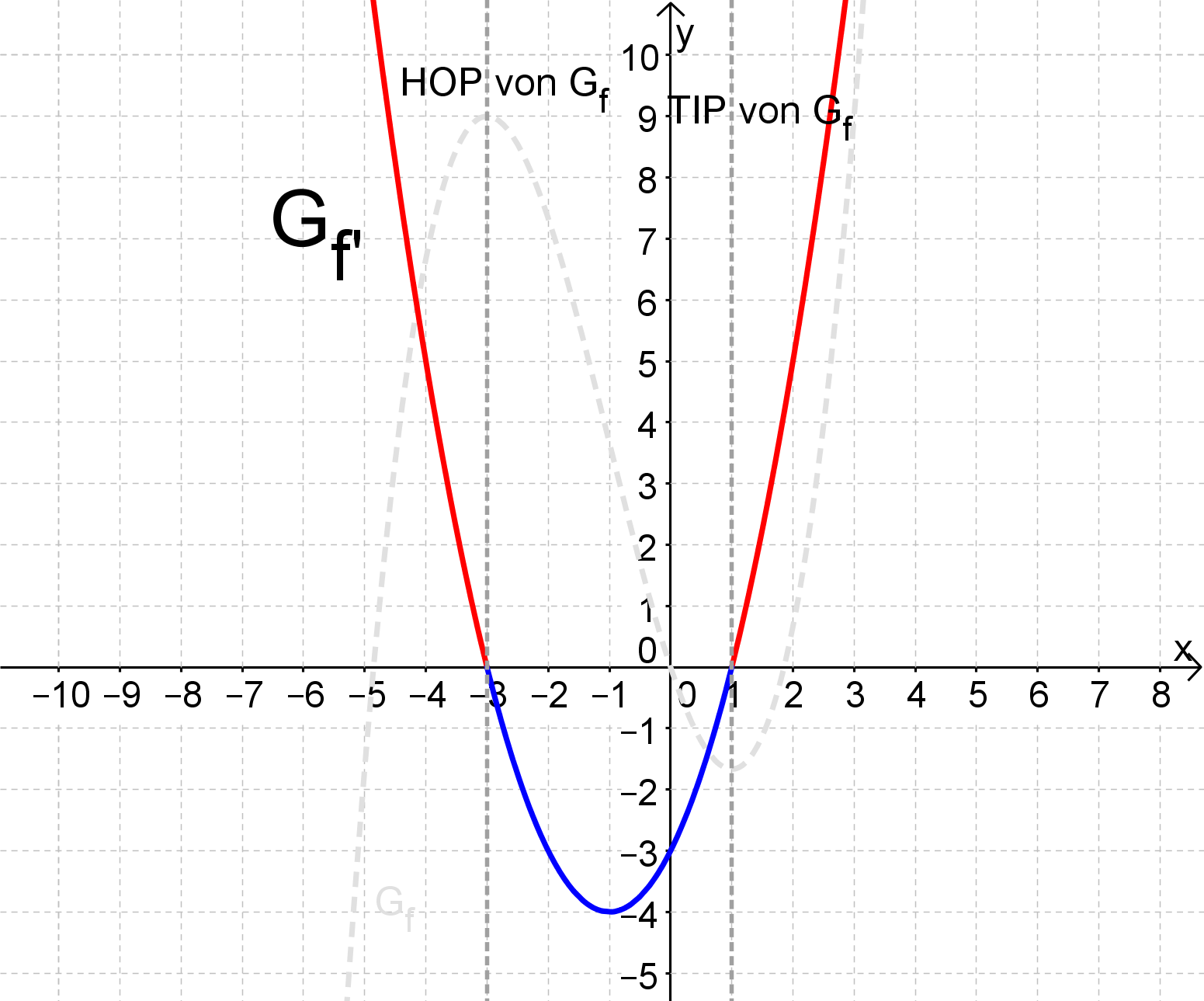
$G_{f}$ ist sms für $x \in] - \infty; - 3]$ und $x \in [1; + \infty [$ und smf für $x \in [- 3; 1]$
Krümmungsverhalten
Du hast zuvor die Nullstellen von $f^{''}$ mit ihren Vielfachheiten berechnet. Gemeinsam mit dem Grad und Leitkoeffizient von $f^{''}$ kannst du den Graphen der 2. Ableitung skizzieren.
Ist der Graph der 2. Ableitung oberhalb der x-Achse, so ist $f^{''} (x) > 0$ und der Graph der Ausgangsfunktion $G_{f}$ ist dort linksgekrümmt.
Analog: ist der Graph der Ableitungsfunktion unterhalb der x-Achse, so ist $f^{''} (x) < 0$ und der Graph der Ausgangsfunktion $G_{f}$ ist dort rechtsgekrümmt.
Wechselt der Graph von $f^{''}$ an einer seiner Nullstellen das Vorzeichen, so hat der Graph $G_{f}$ dort einen Wendepunkt.
Wechselt der Graph von $f^{''}$ an einer Nullstelle das Vorzeichen nicht (die Nullstelle von $f^{''}$ hat eine gerade Vielfachheit), so hat $G_{f}$ dort keinen Wendepunkt!
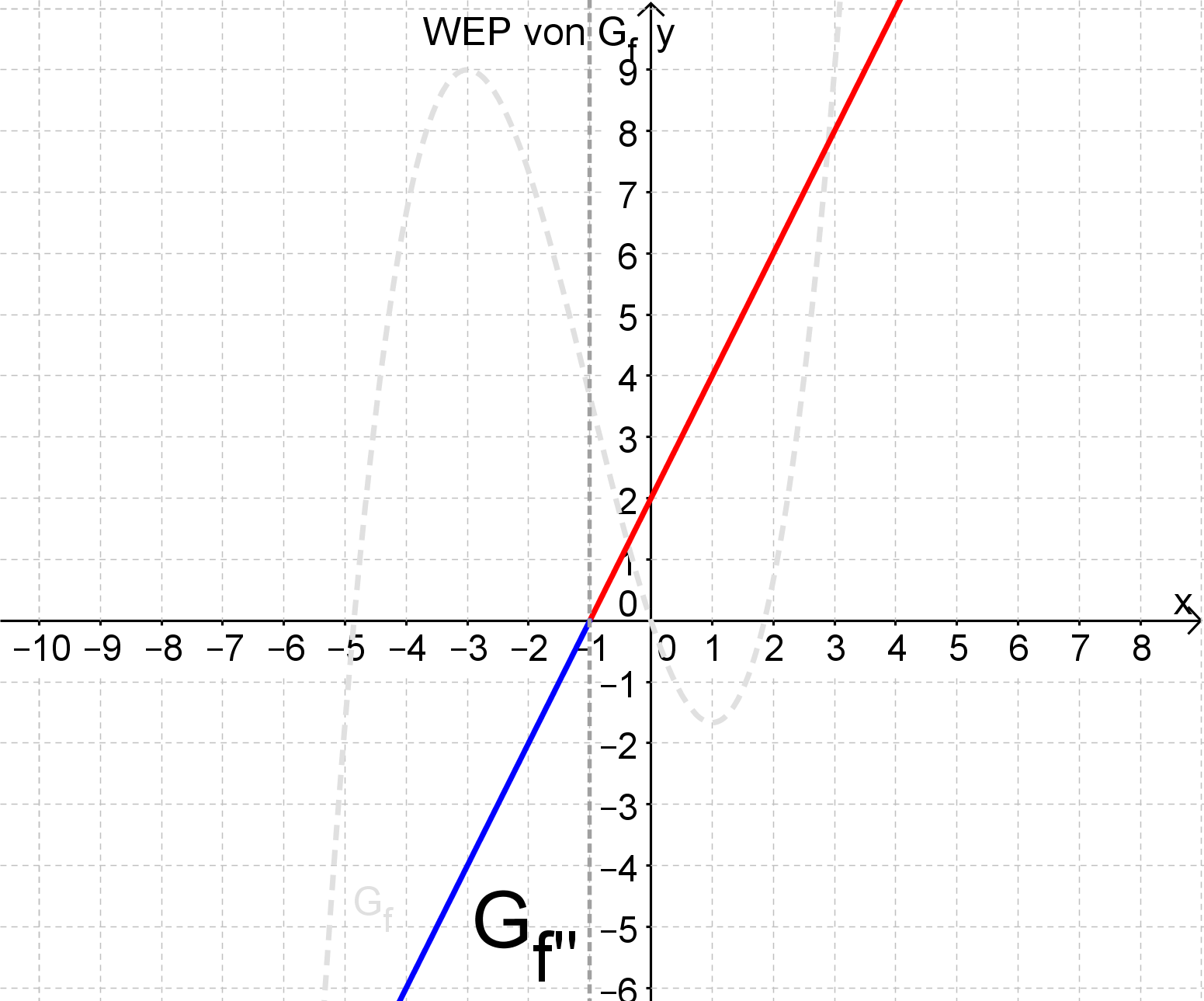
$G_{f}$ ist rgk für $x \in] - \infty; - 1]$ und lgk für $x \in [1; + \infty [$
Vergleich
Der wichtigste Unterschied ist natürlich, dass einmal die 1. Ableitung $f^{'}$ skizziert werden soll und einmal die 2. Ableitung $f^{''}$
Gemeinsamkeiten:
Bei beiden wird mithilfe von Nullstellen mit Vielfachheit, Grad und Leitkoeffizient die jeweilige Ableitungsfunktion skizziert.
Bei beiden interessiert lediglich das Vorzeichen der jeweiligen Ableitung in einem Bereich ("oberhalb oder unterhalb der x-Achse")
Bei beiden muss darauf geachtet werden, ob an der Nullstelle ein Vorzeichenwechsel auftritt oder nicht. Falls dem nicht so ist, liegt dort kein Extrempunkt bzw. Wendepunkt von $G_{f}$ .
Unterschiede:
Wie oben bereits erwähnt, wird einmal $f^{'}$ und einmal $f^{''}$ skizziert.
Es gibt unterschiedliche Arten von Extrempunkten, deshalb ist bei der Skizze von $G_{f^{'}}$ je nach Aufgabe wichtig, von wo nach wo das Vorzeichen wechselt (Art der Extremstelle: Hoch- oder Tiefpunkt). Das ist bei den Wendepunkten egal.
Nachdem du die Nullstellen der 1. Ableitung (Kandidaten für Extremstellen) und der 2. Ableitung (Kandidaten für Wendestellen) bestimmt hast, weißt du, wo die jeweiligen Ableitungsfunktionen ihr Vorzeichen ändern.
Das Vorzeichen von $f^{'}$ in einem Intervall gibt an, ob $G_{f}$ dort steigt ( $f^{'} (x) > 0)$ oder fällt $(f^{'} (x) < 0)$ .
Das Vorzeichen von $f^{''}$ in einem Intervall gibt an, ob $G_{f}$ dort links- $(f^{''} (x) > 0)$ oder rechtsgekrümmt $(f^{''} (x) < 0)$ ist.

Statt mit einer Skizze kannst du das Monotonie- und Krümmungsverhalten auch mithilfe von Tabellen untersuchen. Wodurch unterscheiden sich die Monotonietabelle und die Krümmungstabelle voneinander?

Beispiel Monotonietabelle
Eine Monotonietabelle kann z.B. wie folgt aussehen:
x<
-3
<x<
2
<x<
5
<x
Vorzeichen $f^{'}$
-
0
+
0
+
0
-
Verlauf $G_{f}$
$↘$
smf
TIP
$↗$
sms
TEP
$↗$
sms
HOP
$↘$
smf
Wobei zur Unterteilung der Spalten die Nullstellen der 1. Ableitung verwendet werden.
Beispiel Krümmungstabelle
Eine Krümmungstabelle kann zum Beispiel so aussehen:
x<
-2
<x<
2
<x
Vorzeichen $f^{''}$
-
0
+
0
+
Verlauf $G_{f}$
rgk
WEP
lgk
------
lgk
Wobei zur Unterteilung der Spalten die Nullstellen der 2. Ableitung verwendet wurden.
Vergleich
Beide Tabellen haben drei Zeilen.
Bei beiden Tabellen wird in der ersten Zeile die x-Achse in mehrere Bereiche unterteilt. Allerdings wird sie einmal bei den Nullstellen der 1. Ableitung und einmal bei denen der 2. Ableitung "zerschnitten".
Bei beiden Tabellen kannst du unter die 2. Zeile unter die gefundenen Nullstellen eine 0 schreiben, denn dort ist $f^{'} (x) = 0$ bzw. $f^{''} (x) = 0$ .
In der zweiten Zeile geht es bei beiden Tabellen um das Vorzeichen in einem Bereich, jedoch erneut einmal um das der 1. Ableitung, einmal um das der 2. Ableitung.
In der 3. Zeile sind bei beiden Tabellen die Informationen über $G_{f}$ . Diese unterscheiden sich jedoch am stärksten. In der Monotonietabelle werden die Kürzel $sms, smf, TIP, HOP, TEP$ eingetragen, in die Krümmungstabelle $lgk, rgk$ und $WEP$ .
Nachdem du die Nullstellen der 1. Ableitung (Kandidaten für Extremstellen) und der 2. Ableitung (Kandidaten für Wendestellen) bestimmt hast, weißt du, wo die jeweiligen Ableitungsfunktionen ihr Vorzeichen ändern.
Das Vorzeichen von $f^{'}$ in einem Intervall gibt an, ob $G_{f}$ dort steigt ( $f^{'} (x) > 0)$ oder fällt $(f^{'} (x) < 0)$ .
Das Vorzeichen von $f^{''}$ in einem Intervall gibt an, ob $G_{f}$ dort links- $(f^{''} (x) > 0)$ oder rechtsgekrümmt $(f^{''} (x) < 0)$ ist.
9
Gegeben ist die Funktion $f (x) = e^{x^{2} - 2 x}$ mit $D_{f} = ℝ$ und dem Graph $G_{f}$ .
Bestimme die Art und Lage des Extrempunktes.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema berechnen
Ableitungsfunktion bestimmen
Du benötigst die Kettenregel, da du eine e-Funktion ableiten musst.
$f^{'} (x) = (2 x - 2) e^{x^{2} - 2 x}$
Nullstellen der Ableitung
Die Kandidaten für Extremstellen von $f$ liegen bei den Nullstellen von $f^{'}$ :
$f^{'} (x)$ $=$ $0$
$(2 x - 2) e^{x^{2} - 2 x}$ $=$ $0$
↓
Nach dem Satz vom Nullprodukt kann man die Faktoren einzeln betrachten. Dabei liefert $e^{x^{2} - 2 x}$ keine Nullstellen, da $e^{x} > 0$ für alle x.
$2 x - 2$ $=$ $0$ $+ 2$
$2 x$ $=$ $2$ $: 2$
$x$ $=$ $1$
Da die Nullstelle die Vielfachheit 1 hat, wird bei $x = 1$ eine Extremstelle von f liegen.
Art der Extremstelle
Leite $f^{'} (x) = (2 x - 2) e^{x^{2} - 2 x}$ nochmal ab, um die Art der Extremstelle mit der 2. Ableitung zu bestimmen. Du brauchst nun zusätzlich die Produktregel.
$f^{''} (x)$ $=$ $2 \cdot e^{x^{2} - 2 x} + (2 x - 2) \cdot (2 x - 2) e^{x^{2} - 2 x}$
↓
Klammere $e^{x^{2} - 2 x}$ aus
$=$ $e^{x^{2} - 2 x} \cdot (2 + {(2 x - 2)}^{2})$
↓
Multipliziere mit der binomischen Formel aus.
$=$ $e^{x^{2} - 2 x} \cdot (2 + 4 x^{2} - 8 x + 4)$
$=$ $e^{x^{2} - 2 x} \cdot (4 x^{2} - 8 x + 6)$
Setze deinen gefundenen Kandidaten $x = 1$ in die 2. Ableitung ein:
$f^{''} (1) = e^{- 1} \cdot 2 > 0$ und somit liegt bei $x = 1$ ein Tiefpunkt.
Lage der Extremstelle
Setze $x = 1$ in f ein, um den zugehörigen Funktionswert zu bestimmen:
$f (1) = e^{- 1} = \frac{1}{e}$
Der Graph hat also den Tiefpunkt $T I P (1 | \frac{1}{e})$
Um die Art und Lage eines Extrempunktes zu bestimmen, musst du folgende Schritte ausführen:
Bilde die erste Ableitung $f^{'}$
Bestimme die Nullstellen von $f^{'}$
Bestimme die Art der Extremstelle über die Monotonietabelle oder die 2. Ableitung
Setze in den Term von $f$ ein, um die y-Koordinate des Extrempunktes zu ermitteln.

Untersuche, ob der Graph Wendepunkte besitzt und gib sein Krümmungsverhalten an. Folgere daraus, ob es Stellen stärkster Zu- oder Abnahme gibt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Krümmungsverhalten eines Funktionsgraphen
Nullstellen der zweiten Ableitung
In der ersten Teilaufgabe hast du bereits die zweite Ableitung bestimmt. Suche jetzt nach ihren Nullstellen.
$f^{''} (x)$ $=$ $0$
$e^{x^{2} - 2 x} \cdot (4 x^{2} - 8 x + 6)$ $=$ $0$
↓
Nach dem Satz vom Nullprodukt kann jeder Faktor einzeln betrachtet werden. $e^{x^{2} - 2 x}$ hat allerdings keine Nullstellen, da $e^{x} > 0$ für alle $x \in ℝ$
$4 x^{2} - 8 x + 6$ $=$ $0$
Verwende die Mitternachtsformel, um die Lösungen der Gleichung zu bestimmen:
$x_{1 / 2} = \frac{- (- 8) \pm \sqrt{(- 8)^{2} - 4 \cdot 4 \cdot 6}}{2 \cdot 4} = \frac{8 \pm \sqrt{- 32}}{8}$
Da die Diskriminante $D = - 32$ negativ ist, gibt es keine Lösungen.
Somit hat der Graph keine Wendepunkte.
Krümmungsverhalten
Es gibt keine Wendepunkte. Also hat der Graph auf der gesamten Definitionsmenge die gleiche Krümmung.
Du kannst eine beliebige Zahl einsetzen, um diese Krümmung herauszufinden:
$f^{''} (0) = 6 > 0$ also ist der Graph für alle $x \in ℝ$ linksgekrümmt.
Stellen stärkster Zu- oder Abnahme
Da der Graph keine Wendepunkte hat, kann es keine Stellen lokal stärkster Zu- oder Abnahme geben.
Für die Bestimmung von Wendepunkte und Krümmungsverhalten gehst du folgendermaßen vor:
Bestimme die 2. Ableitung
Bestimme die Nullstellen der 2. Ableitung. Falls es keine gibt, gibt es keine Wendepunkte
Das Krümmungsverhalten hängt vom Vorzeichen der 2. Ableitung ab. Falls es Wendepunkte gibt, fertige eine Krümmungstabelle an.
Die notwendige Vorraussetzung für eine Stelle stärkster Zu- oder Abnahme ist ein Wendepunkt.

Bestimme die Schnittpunkte mit den Koordinatenachsen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkte mit den Koordinatenachsen
Schnittpunkt mit der y-Achse
Setze $x = 0$ ein.
$f (0) = e^{0^{2} - 2 \cdot 0} = e^{0} = 1$
Der Schnittpunkt ist $S_{y} (0 | 1)$
Schnittpunkte mit der x-Achse
Setze mit 0 gleich.
$f (x)$ $=$ $0$
$e^{x^{2} - 2 x}$ $=$ $0$
Diese Gleichung hat keine Lösung, denn $e^{x} > 0$ für alle $x \in ℝ$ und somit hat auch jede andere Exponentialfunktion $e^{g (x)}$ (mit $g (x)$ ganzrationale Funktion) keine Nullstellen.
Es gibt keine Schnittpunkte mit der x-Achse.
Für den Schnittpunkt mit der y-Achse musst du $x = 0$ einsetzen
Für die Schnittpuntke mit der x-Achse musst du den Term mit 0 gleichsetzen, also $f (x) = 0$
Vergiss nicht, die Koordinaten als Punkte anzugeben!

Gib den Globalverlauf von f für $x \to \pm \infty$ an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwertbetrachtung
Arbeite dich vom Exponenten aus vor:
$\lim_{x \to - \infty} f (x)$ $=$ $\lim_{x \to - \infty} (e^{x^{2} - 2 x})$
↓
Im Exponenten dominiert $" (- \infty)^{2} " = " + \infty "$
$=$ $\lim_{x \to - \infty} (e^{" + \infty "})$
↓
Verlauf der natürlichen Exponentialfunktion
$=$ $+ \infty$
Für $x \to + \infty$ kannst du genauso vorgehen:
$\lim_{x \to + \infty} f (x)$ $=$ $\lim_{x \to + \infty} (e^{x^{2} - 2 x})$
↓
Im Exponenten dominiert $" (+ \infty)^{2} " = " + \infty "$
$=$ $\lim_{x \to - \infty} (e^{" + \infty "})$
↓
Verlauf der natürlichen Exponentialfunktion
$=$ $+ \infty$
Der Graph hat also keine Asymptoten.
Betrachte zuerst das Verhalten des Exponenten und dann das Verhalten der Exponentialfunktion.

Zeichne den Graphen $G_{f}$ für $x \in [0; 2,5]$ , wobei auf beiden Achsen $2 c m \hat{=} 1 L E$ gilt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
Fertige eine Wertetabelle für f mit den Grenzen 0 und 2,5 und der Schrittweite 0,25 an.
In deinem Koordinatensystem ist auf beiden Achsen erst bei 2cm die Zahl 1 anzutragen:
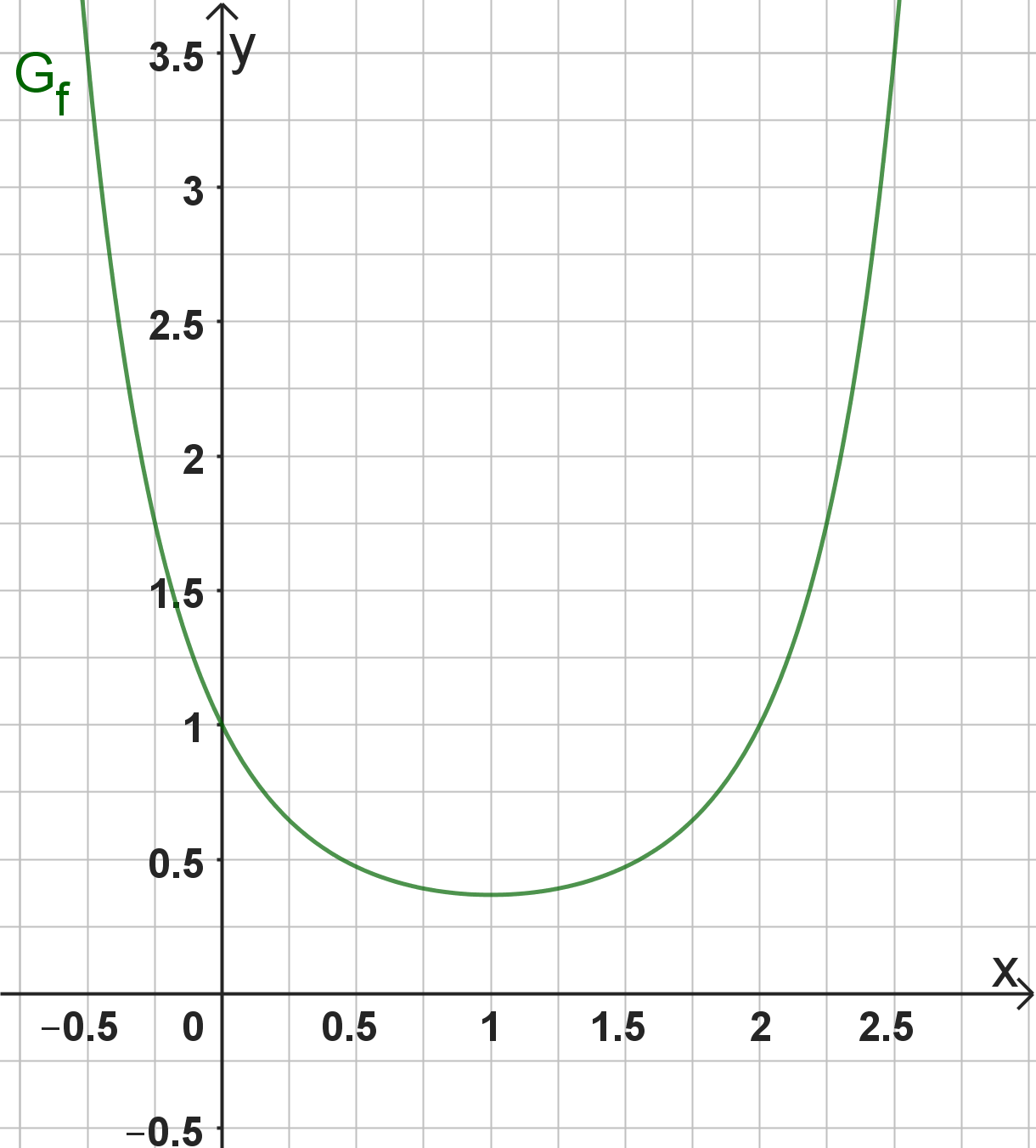
Fertige eine Wertetabelle an und wähle die Schrittweite 0,25. So kannst du bei jedem Kästchen einen Punkt einzeichnen und erhältst ein genau genuges Ergebnis.

	x<	-3	<x<	2	<x<	5	<x
Vorzeichen $f^{'}$	-	0	+	0	+	0	-
Verlauf $G_{f}$	$↘$ smf	TIP	$↗$ sms	TEP	$↗$ sms	HOP	$↘$ smf

	x<	-2	<x<	2	<x
Vorzeichen $f^{''}$	-	0	+	0	+
Verlauf $G_{f}$	rgk	WEP	lgk	------	lgk

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$\frac{(2 x^{2} - 2) \cdot \ln ({(x - 1)}^{2})}{1 + x}$	$=$	$\frac{2 (x^{2} - 1) \cdot \ln ({(x - 1)}^{2})}{1 + x}$
	↓	Im Nenner kommt eine 3. binomische Formel vor. Forme diese um.
	$=$	$\frac{2 ((x - 1) (x + 1)) \cdot \ln ({(x - 1)}^{2})}{1 + x}$
	↓	Kürze $(1 + x)$ .
	$=$	$2 (x - 1) \cdot \ln ({(x - 1)}^{2})$

$g^{'} (x)$	$=$	$u^{'} (x) \cdot v (x) + u (x) \cdot v^{'} (x)$
	↓	Setze in die Formel für die Produktregel ein.
	$=$	$- \frac{1}{2} \cdot \sqrt{x + 2} - \frac{x}{2} \cdot \frac{1}{2 \cdot \sqrt{x + 2}}$
	↓	Vereinfache.
	$=$	$- \frac{\sqrt{x + 2}}{2} - \frac{x}{4 \cdot \sqrt{x + 2}}$
	↓	Setze $g^{'} (x) = 0$ .
$0$	$=$	$- \frac{\sqrt{x + 2}}{2} - \frac{x}{4 \cdot \sqrt{x + 2}}$	$+ \frac{x}{4 \cdot \sqrt{x + 2}}$
	↓	Löse nach $x$ auf.
$\frac{x}{4 \cdot \sqrt{x + 2}}$	$=$	$- \frac{\sqrt{x + 2}}{2}$	$\cdot (4 \cdot \sqrt{x + 2})$
$x$	$=$	$- \frac{\sqrt{x + 2}}{2} \cdot 4 \cdot \sqrt{x + 2}$
	↓	Kürze und fasse die Wurzeln zusammen.
$x$	$=$	$- 2 \cdot (x + 2)$
	↓	Löse die Klammer auf.
$x$	$=$	$- 2 x - 4$	$+ 2 x$
$3 x$	$=$	$- 4$	$: 3$
$x$	$=$	$- \frac{4}{3}$

$\lim_{x \to 1^{-}} f (x)$	$=$	$\lim_{x \to 1^{-}} 2 \underset{= 0}{\underset{⏟}{(x - 1)}} \underset{\to - \infty}{\underset{⏟}{\ln ({(x - 1)}^{2})}}$
	$=$	$\lim_{x \to 1^{-}} \frac{\overset{\to - \infty}{\overset{⏞}{\ln ({(x - 1)}^{2})}}}{\underset{\to - \infty}{\underset{⏟}{\frac{1}{2 (x - 1)}}}}$
	↓	Du leitest jetzt Zähler und Nenner separat ab.
	$=$	$\lim_{x \to 1^{-}} \frac{\frac{2 (x - 1)}{{(x - 1)}^{2}}}{- \frac{1}{2 {(x - 1)}^{2}}}$
	$=$	$\lim_{x \to 1^{-}} \frac{- 2 {(x - 1)}^{2} \cdot 2 (x - 1)}{{(x - 1)}^{2}}$
	$=$	$\lim_{x \to 1^{-}} - 4 (x - 1)$
	$=$	$0$

$f (p)$	$=$	$f^{'} (p) \cdot p + t$
$2 \cdot (p - 1) \ln ({(p - 1)}^{2})$	$=$	$2 \cdot (\ln ({(p - 1)}^{2}) + 2) \cdot p + t$
	↓	Bringe t auf eine Seite der Gleichung.
$t$	$=$	$2 (p - 1) \ln ({(p - 1)}^{2}) - 2 (\ln ({(p - 1)}^{2}) + 2) p$
$t$	$=$	$2 \cdot \ln ({(p - 1)}^{2}) \cdot ((p - 1) - p) - 4 p$
$t$	$=$	$- 2 \cdot \ln ({(p - 1)}^{2}) - 4 p$

$e^{- \sqrt{k x_{0}}}$	$=$	$\frac{- k \cdot e^{- \sqrt{k x_{0}}}}{2 \sqrt{k x_{0}}} \cdot x_{0} + t_{1}$
$e^{- \sqrt{k x_{0}}}$	$=$	$\frac{- k \cdot e^{- \sqrt{k x_{0}}}}{2 \sqrt{k x_{0}}} \cdot x_{0} + \frac{- k \cdot e^{- \sqrt{k x_{0}}}}{2 \sqrt{k x_{0}}}$	$: (\frac{- k \cdot e^{- \sqrt{k x_{0}}}}{2 \sqrt{k x_{0}}})$
$\frac{2 \sqrt{k x_{0}}}{- k}$	$=$	$x_{0} + 1$	$^{2}$
$\frac{4 k x_{0}}{k^{2}}$	$=$	$x_{0}^{2} + 2 x_{0} + 1$	$\cdot k^{2}$
$0$	$=$	$k^{2} x_{0}^{2} + (2 k^{2} - 4 k) x_{0} + k^{2}$

$f (x)$	$=$	$\frac{x + 1}{x^{2} - 4}$
	↓	Berechne die Nullstellen des Nenners.
$x^{2} - 4$	$=$	$0$
$x^{2}$	$=$	$4$
	↓	Die Nullstellen des Nenners sind die Definitionslücken der Funktion.
$x_{1}$	$=$	$- 2$
$x_{2}$	$=$	$2$

$f (x)$	$=$	$\frac{x + 1}{x^{2} - 4}$
	↓	Setze 0 in die Funktion ein.
$f (0)$	$=$	$\frac{0 + 1}{0^{2} - 4}$
$f (0)$	$=$	$- \frac{1}{4}$

$f (x)$	$=$	$\frac{x + 1}{x^{2} - 4}$
	↓	Berechne die Nullstelle des Zählers.
$x + 1$	$=$	$0_{}$
$x$	$=$	$- 1$

$f (x)$	$=$	$\frac{x + 1}{x^{2} - 4}$
	↓	Für die Tangente benötigt man eine Steigung. Dafür berechnet man die Ableitung.
$f ´ (x)$	$=$	$\frac{1 \cdot (x^{2} - 4) - 2 x (x + 1)}{(x^{2} - 4)^{2}}$
	↓	Für die Tangente an der Stelle $x = 0$ benötigt man die Ableitung an der Stelle. Setze 0 in die Ableitung ein.
	$=$	$\frac{- x^{2} - 2 x - 4}{(x^{2} - 4)^{2}}$
$f ´ (0)$	$=$	$\frac{- 0^{2} - 2 \cdot 0 - 4}{(0^{2} - 4)^{2}}$
	$=$	$\frac{- 4}{16}$
	$=$	$- \frac{1}{4}$
	↓	Nachdem man die Steigung weiß, benötigt man noch die vollständigen Koordinaten des Punktes. Dafür setzt man den x-Wert in die Funktion ein.

$f (x)$	$=$	$\frac{x + 1}{x^{2} - 4}$
	↓	Für die Extremstellen sind die Nullstellen der Ableitung gesucht. Setze die Ableitung $0$ .
$f ´ {(x)}_{}$	$=$	$\frac{- x^{2} - 2 x - 4}{(x^{2} - 4)^{2}}$
	$=$	$0$
	↓	Löse nach $x$ auf.
$- x^{2} - 2 x - 4$	$=$	$0$
$x^{2} + 2 x + 4$	$=$	$0$
$x$	$=$	$\frac{- 2 \pm \sqrt{2^{2} - 4 \cdot 4 \cdot 1}}{2 \cdot 1}$
	$=$	$\frac{- 2 \pm \sqrt{- 12}}{2}$
	↓	Die Wurzel aus einer negativen Zahl gibt es im Reellen nicht, also gibt es keine Lösung für $x$ . Die Funktion hat keine Extremstellen.

$g (x)$	$=$	$- \frac{x}{2} \cdot \sqrt{x + 2}$
	↓	Setze $g (x) = 0$ .
$0$	$=$	$- \frac{x}{2} \cdot \sqrt{x + 2}$
	↓	Ein Produkt ist dann gleich null, wenn ein Faktor null ist (Satz vom Nullprodukt)
$x_{1}$	$=$	$0$
	↓	Setze nun den zweiten Faktor gleich null.
$0$	$=$	$\sqrt{x + 2}$	$()^{2}$
	↓	Löse nach $x$ auf.
$0$	$=$	$x + 2$	$- 2$
$x_{2}$	$=$	$- 2$

$g (x)$	$=$	$- \frac{x}{2} \cdot \sqrt{x + 2}$
	↓	Setze $x = 1$ ein.
$g (1)$	$=$	$- \frac{1}{2} \cdot \sqrt{1 + 2}$
	$=$	$= - \frac{1}{2} \cdot \sqrt{3}$
	$\approx$	$- 0,87$

$x + 2$	$\geq$	$0$	$- 2$
$x$	$\geq$	$- 2$

$g (x)$	$=$	$- \frac{x}{2} \cdot \sqrt{x + 2}$
	↓	Setze $x = - \frac{4}{3}$ ein.
$g (- \frac{4}{3})$	$=$	$- \frac{(- \frac{4}{3})}{2} \cdot \sqrt{- \frac{4}{3} + 2}$
	↓	Vereinfache
	$=$	$\frac{2}{3} \cdot \sqrt{\frac{2}{3}}$
	$\approx$	$0,54$

$f^{'} (x)$	$=$	$0$
$(2 x - 2) e^{x^{2} - 2 x}$	$=$	$0$
	↓	Nach dem Satz vom Nullprodukt kann man die Faktoren einzeln betrachten. Dabei liefert $e^{x^{2} - 2 x}$ keine Nullstellen, da $e^{x} > 0$ für alle x.
$2 x - 2$	$=$	$0$	$+ 2$
$2 x$	$=$	$2$	$: 2$
$x$	$=$	$1$

$f^{''} (x)$	$=$	$2 \cdot e^{x^{2} - 2 x} + (2 x - 2) \cdot (2 x - 2) e^{x^{2} - 2 x}$
	↓	Klammere $e^{x^{2} - 2 x}$ aus
	$=$	$e^{x^{2} - 2 x} \cdot (2 + {(2 x - 2)}^{2})$
	↓	Multipliziere mit der binomischen Formel aus.
	$=$	$e^{x^{2} - 2 x} \cdot (2 + 4 x^{2} - 8 x + 4)$
	$=$	$e^{x^{2} - 2 x} \cdot (4 x^{2} - 8 x + 6)$

$f^{''} (x)$	$=$	$0$
$e^{x^{2} - 2 x} \cdot (4 x^{2} - 8 x + 6)$	$=$	$0$
	↓	Nach dem Satz vom Nullprodukt kann jeder Faktor einzeln betrachtet werden. $e^{x^{2} - 2 x}$ hat allerdings keine Nullstellen, da $e^{x} > 0$ für alle $x \in ℝ$
$4 x^{2} - 8 x + 6$	$=$	$0$

$\lim_{x \to - \infty} f (x)$	$=$	$\lim_{x \to - \infty} (e^{x^{2} - 2 x})$
	↓	Im Exponenten dominiert $" (- \infty)^{2} " = " + \infty "$
	$=$	$\lim_{x \to - \infty} (e^{" + \infty "})$
	↓	Verlauf der natürlichen Exponentialfunktion
	$=$	$+ \infty$

$\lim_{x \to + \infty} f (x)$	$=$	$\lim_{x \to + \infty} (e^{x^{2} - 2 x})$
	↓	Im Exponenten dominiert $" (+ \infty)^{2} " = " + \infty "$
	$=$	$\lim_{x \to - \infty} (e^{" + \infty "})$
	↓	Verlauf der natürlichen Exponentialfunktion
	$=$	$+ \infty$

Aufgaben zur Kurvendiskussion

Definitionsbereich

Der Nenner darf nicht Null werden.

Das Argument des Logarithmus muss größer als 0 sein.

Definitionsmenge

Art der Definitionslücken

Definitionslücke x=−1

Definitionslücke x=1

Grenzwert im Unendlichen

Grenzwert an den Definitionslücken von beiden Seiten

Grenzwerte an x=−1

Grenzwerte an x=1

Waagerechte Asymptoten

Senkrechte Asymptoten

Schiefe Asymptoten

Extremstelle berechnen

Koordinaten der Extrempunkte

Art der Extrempunkte bestimmen

Art der Extrempunkte (formal)

Art der Extrempunkte (einfacher)

Lage der Wendepunkte

Grenzen des Wertebereichs

Lücken im Wertebereich

Symmetrie zum Ursprung / zur y-Achse

Symmetrie zum vermuteten Symmetriezentrum

x- Werte bestimmen

y-Werte bestimmen

Version 1: Partielle Integration

Version 2: Substitution

Schnittpunkte der Graphen

Flächenberechnung

Was wir wissen

Umfang

Flächeninhalt

Methode 1: Analytische Geometrie in der Ebene

Methode 2: Aufspalten in Dreiecke

Waagerechte Asymptoten

Senkrechte Asymptoten

1. Ableitung

Monotonieverhalten

2. Ableitung

Krümmungsverhalten

Nullstellen der ersten Ableitung

Funktionswerte an den Grenzen des Definitionsbereichs

1. Tangente: k<0

2. Tangente: k > 0

1. Substitution

2. Partielle Integration

3. Resubstitution

Graphen zeichnen

Berechnung der Anfangshöhe des Setzlings

Wachstum der Pflanze in sechs Wochen

Maximale Wachstumsrate

Maximale Wachstumsrate

Maximale Höhe der Maispflanze

Begründung der Lösung

Bestimmung des Koeffizienten

Gegenargument gegen Funktion f1

Gegenargument gegen Funktion f2

Gegenargument gegen Funktion f3

Begründung für Funktion f4

Graphenzuordnung

Monotonieverhalten

Krümmungsverhalten

Vergleich

Monotonieverhalten über Skizze von Gf′

Krümmungsverhalten

Vergleich

Beispiel Monotonietabelle

Beispiel Krümmungstabelle

Vergleich

Ableitungsfunktion bestimmen

Nullstellen der Ableitung

Art der Extremstelle

Lage der Extremstelle

Nullstellen der zweiten Ableitung

Krümmungsverhalten

Stellen stärkster Zu- oder Abnahme

Schnittpunkt mit der y-Achse

Schnittpunkte mit der x-Achse

Definitionslücke $x = - 1$

Definitionslücke $x = 1$

Grenzwerte an $x = - 1$

Grenzwerte an $x = 1$

1. Tangente: $k < 0$

Gegenargument gegen Funktion $f_{1}$

Gegenargument gegen Funktion $f_{2}$

Gegenargument gegen Funktion $f_{3}$

Begründung für Funktion $f_{4}$

Monotonieverhalten über Skizze von $G_{f^{'}}$