Wurzelfunktion

Wurzelfunktionen sind Potenzfunktionen in der Form, dass die Variable unter einer Wurzel steht. Sie bilden damit die Umkehrfunktionen zu Potenzfunktionen der Form $f (x) = x^{n}$ mit $n \in ℕ$ .

Ihre einfachste Form ist:

$f (x) = \sqrt[n]{x} = x^{\frac{1}{n}} mit n \in ℕ, x \in ℝ_{0}^{+}$

Die bekanntesten Wurzelfunktionen sind die "zweite" und die "dritte" Wurzel.

$f (x) = \sqrt[2]{x} = \sqrt{x} und g (x) = \sqrt[3]{x}$

(Bei der zweiten Wurzel wird meist die kleine 2 weggelassen.)

Graphen der ersten Wurzelfunktionen

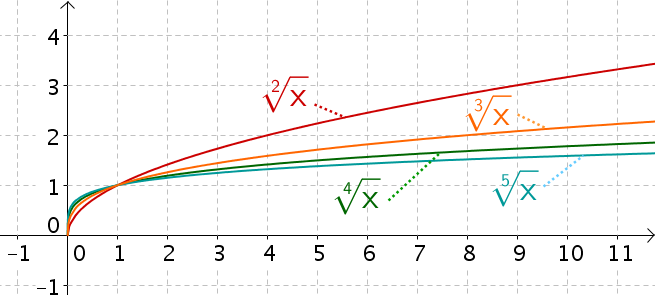
Geogebra File: https://assets.serlo.org/legacy/9285_wRU7USKTAS.xml

Grenzwerte und Monotonie

Grenzwerte

Auch wenn die Wurzelfunktionen vergleichsweise "klein" sind - sie also weniger stark wachsen als alle Geraden und Potenzfunktionen - ist ihr Grenzwert im Unendlichen stets unendlich. Beachte dabei, dass hier $x$ gegen unendlich geht, und nicht $n$ .

\lim_{x \to \infty} \sqrt[n]{x} = \infty

Am linken Rand des Definitionsbereichs gehen die Wurzelfunktionen gegen $0$ :

\lim_{x \to 0} \sqrt[n]{x} = 0

Monotonie

Wurzelfunktionen sind streng monoton steigend.

Ableitungen

Die Ableitungen der Wurzelfunktion lassen sich mit den Ableitungsregeln für Polynome berechnen.

1. Ableitung

Allgemein:

${(\sqrt[n]{x})}^{'}$	$=$	${(x^{\frac{1}{n}})}^{'}$
	↓	Wende die Ableitungsregel für Polynome an.
	$=$	$\frac{1}{n} x^{\frac{1}{n} - 1}$
	↓	Nun kannst du noch ein wenig umformen.
	$=$	$\frac{1}{n} x^{\frac{1 - n}{n}}$
	$=$	$\frac{1}{n} \sqrt[n]{x^{1 - n}}$

Beispiel für $n = 2$ :

${(\sqrt{x})}^{'}$	$=$	${(x^{\frac{1}{2}})}^{'}$
	$=$	$\frac{1}{2} x^{\frac{1}{2} - 1}$
	$=$	$\frac{1}{2} x^{- \frac{1}{2}}$
	$=$	$\frac{1}{2 \sqrt{x}}$

2. Ableitung

Die zweite Ableitung berechnet sich durch das Ableiten der 1. Ableitung. Für $n = 2$ wäre das:

${(\sqrt{x})}^{''}$	$=$	${(\frac{1}{2 \sqrt{x}})}^{'}$
	$=$	${(\frac{1}{2} x^{- \frac{1}{2}})}^{'}$
	$=$	$- \frac{1}{4} x^{- \frac{1}{2} - 1}$
	$=$	$- \frac{1}{4} x^{- \frac{3}{2}}$
	$=$	$\frac{1}{4 \sqrt{x^{3}}}$