Teil 1, Analysis

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
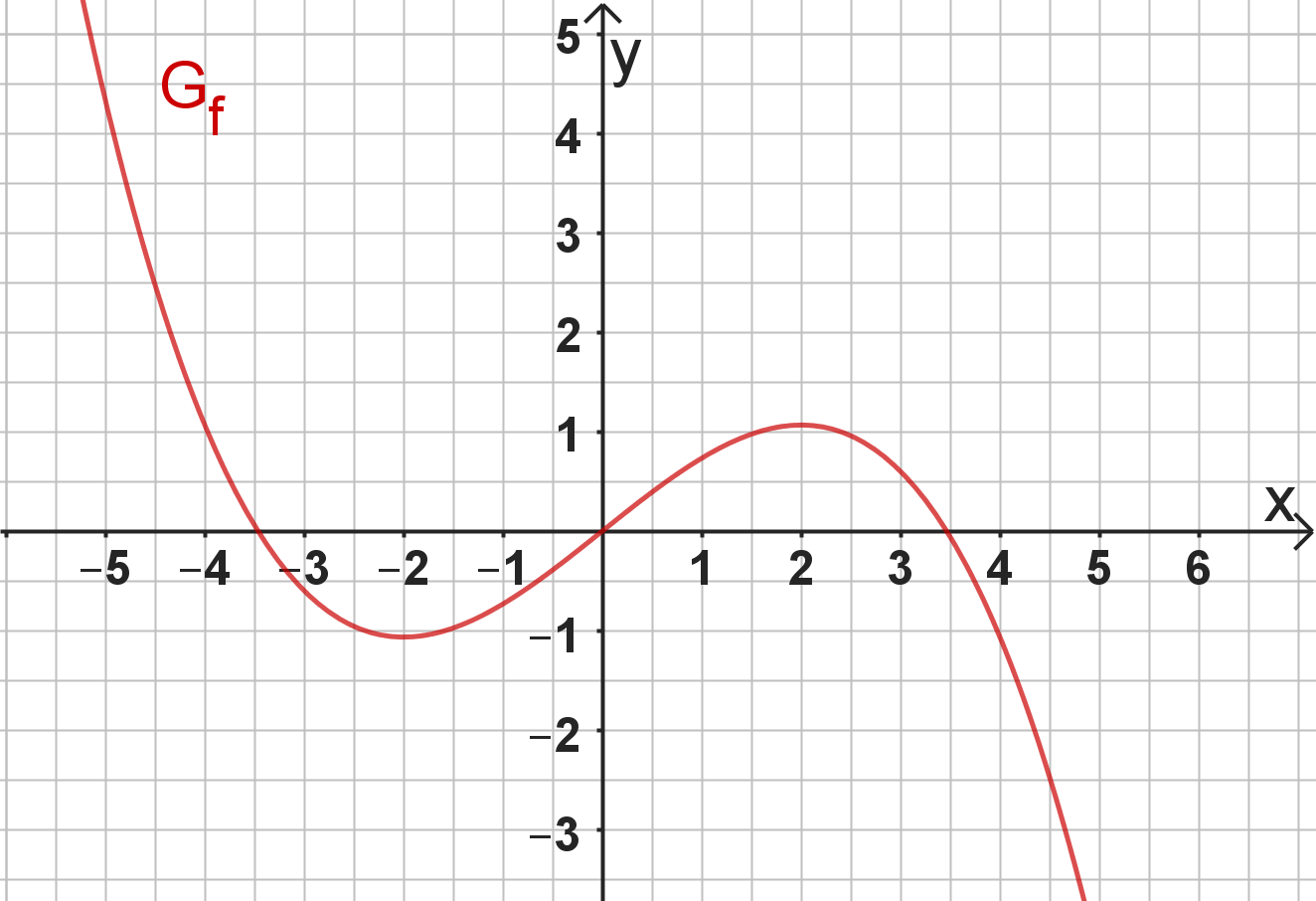
Der zum Ursprung eines kartesischen Koordinatensystems punktsymmetrische Graph $G_{f}$ einer ganzrationalen Funktion $f$ dritten Grades mit der Definitionsmenge $D_{f} = ℝ$ besitzt einen lokalen Tiefpunkt an der Stelle $x = - 2$ .
Skizzieren Sie mithilfe der oben genannten Eigenschaften von $f$ einen möglichen Graphen dieser Funktion und geben Sie das Verhalten der Funktionswerte $f (x)$ für $x \to - \infty$ und $x \to \infty$ an. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ganzrationale Funktionen (Polynomfunktionen)
Graph skizzieren
Da der Graph der ganzrationalen Funktion punktsymmetrisch zum Ursprung ist, verläuft er durch den Ursprung.
Markiere den Tiefpunkt bei $x = - 2$ . Aufgrund der Symmetrie ist außerdem bei $x = 2$ ein Hochpunkt.
Da der Grad der Funktion 3 ist, gibt es maximal zwei Extremstellen. Diese sind bei $x = 2$ und $x = - 2$ . Es gibt also keine weiteren als die oben beschriebenen.
möglicher Graph
Globalverlauf
Wenn du den Graph korrekt skizziert hast, kannst du den Globalverlauf jetzt direkt ablesen. Verwende zum Beispiel die Limes-Schreibweise:
$\lim_{x \to - \infty} f (x) = + \infty$
und
$\lim_{x \to + \infty} f (x) = - \infty$
Du weißt keine y-Koordinaten
Beachte die Punktsymmetrie: Was lernt man daraus, dass bei $x = - 2$ ein Tiefpunkt ist? Was haben alle Graphen einer punktsymmetrischen, ganzrationalen Funktion gemeinsam?
Ermittle aus deiner Skizze den Globalverlauf.

Beschreiben Sie den Verlauf des Graphen $G_{f^{'}}$ der ersten Ableitungsfunktion $f^{'}$ mit Worten. Geben Sie dabei insbesondere die Nullstellen der Funktion $f^{'}$ , die Lage des Extrempunktes und das Symmetrieverhalten des Graphen $G_{f^{'}}$ an. (4 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung von Funktionen
Der Graph $G_{f^{'}}$ hat bei $x = - 2$ und $x = 2$ einfache Nullstellen (da $G_{f}$ dort Extremstellen hat).
Links von $x = - 2$ und rechts von $x = 2$ verläuft er unterhalb der x-Achse (da $G_{f}$ dort streng monoton fällt), sonst darüber.
Der Graph von $G_{f^{'}}$ ist achsensymmetrisch zur y-Achse (da $G_{f}$ punktsymmetrisch zum Ursprung ist)
Der Extrempunkt von $G_{f^{'}}$ ist ein Hochpunkt. Er liegt auf der y-Achse (aufgrund der Symmetrie von $G_{f^{'}}$ bzw. weil $G_{f^{'}}$ eine Parabel ist, liegt er mittig zwischen den Nullstellen)
Kurz gesagt: Der Graph der Ableitung ist eine nach unten geöffnete Parabel mit den Nullstellen $x = - 2$ und $x = 2$ und dem Scheitelpunkt auf der y-Achse. Er ist achsensymmetrisch zur y-Achse.
Vergiss keinen gefragten Aspekt!
Monotonie und Extrema:
Hat $G_{f}$ eine Extremstelle, so hat $G_{f^{'}}$ dort eine Nullstelle mit Vorzeichenwechsel.
Fällt $G_{f}$ in einem Intervall, so verläuft $G_{f^{'}}$ in diesem Intervall unterhalb der x-Achse (gegenteilig für steigend)
Symmetrie: Ist $G_{f}$ achsensymmetrisch, so ist $G_{f^{'}}$ punktsymmetrisch (und umgekehrt)
Der Extrempunkt von $G_{f^{'}}$ liegt bei der Wendestelle von $G_{f}$ . Außerdem liegt er aufgrund der Symmetrie mittig zwischen den Extremstellen.

Du musst deine Angaben nicht erklären
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Lösen Sie die beiden folgenden Gleichungen über der Grundmenge der reellen Zahlen. (6 BE)
$3 x^{4} - 12 x^{2} = 0$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Binomische Formeln
$3 x^{4} - 12 x^{2}$ $=$ $0$
↓
Klammere $3 x^{2}$ aus
$3 x^{2} (x^{2} - 4)$ $=$ $0$
↓
Verwende die 3. binomische Formel
$3 x^{2} (x + 2) (x - 2)$ $=$ $0$
Laut dem Satz vom Nullprodukt sind die drei Lösungen $x = 0$ , $x = - 2$ und $x = 2$
Klammere aus.
Verwende die 3. binomische Formel. Alternativ geht es auch durch Umformen und Radizieren (Wurzel ziehen).

$e^{x^{2}} = e^{2 x - 1}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialgleichung
$e^{x^{2}}$ $=$ $e^{2 x - 1}$
↓
Da die Basis (e) auf beiden Seiten gleich ist, kannst du die Exponenten vergleichen
$x^{2}$ $=$ $2 x - 1$ $- 2 x + 1$
$x^{2} - 2 x + 1$ $=$ $0$
↓
Das ist die 2. binomische Formel
${(x - 1)}^{2}$ $=$ $0$
Die einzige Lösung ist $x = 1$
Führe einen Exponentenvergleich durch
Verwende die binomischen Formeln oder die Mitternachtsformel
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion $g : x \mapsto e^{0,25 x} - e^{- 0,25 x}$ mit der Definitionsmenge $D_{g} = ℝ$ . Ihr Graph in einem kartesischen Koordinatensystem wird mit $G_{g}$ bezeichnet.
Untersuchen Sie das Symmetrieverhalten des Graphen der Funktion g zum Koordinatensystem und geben Sie $\int_{- 2}^{2} g (x) d x$ an. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
Symmetrienachweis
Setze $- x$ ein
↓
$g (- x)$ $=$ $e^{0,25 \cdot (- x)} - e^{- 0,25 \cdot (- x)}$
$=$ $e^{- 0,25 x} - e^{0,25 x}$
↓
Klammere $- 1$ aus
$=$ $- (- e^{- 0,25 x} + e^{0,25 x})$
$=$ $- (e^{0,25 x} - e^{- 0,25 x})$
$=$ $- g (x)$
Der Graph $G_{g}$ ist also punktsymmetrisch zum Ursprung.
bestimmtes Integral
Da der Graph punktsymmetrisch zum Ursprung ist und die Grenzen gleich weit vom Ursprung entfernt sind, hat das Integral den Wert 0.
Der Graph ist symmetrisch zum Koordinatensystem, wenn entweder $g (- x) = g (x)$ (Achsensymmetrie) oder $g (- x) = - g (x)$ (Punktsymmetrie) gilt. Setze also $- x$ ein und forme um.
Überlege dir, wie deine Erkenntnisse über die Symmetrie die Berechnung des bestimmten Integrals beeinflussen.

Ermitteln Sie die Gleichung für die Tangente an den Graphen der Funktion g an der Stelle $x = 0$ . (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Verwende zum Beispiel die Punkt-Steigungs-Form der linearen Funktion:
Verläuft eine Gerade mit der Steigung m durch den Punkt $P (x_{P} | y_{P})$ , so kann die Gerade durch $y = m (x - x_{P}) + y_{P}$ angegeben werden.
Hier also:
$t (x) = g^{'} (0) \cdot (x - 0) + g (0)$
wobei $m = g^{'} (0)$ der Wert der Ableitung bei $x = 0$ ist und $g (0)$ der Funktionswert.
Da $G_{g}$ aufgrund der Punktsymmetrie durch den Ursprung verläuft, ist $g (0) = 0$
Steigung bestimmen
Verwende die Kettenregel, um $g (x) = e^{0,25 x} - e^{- 0,25 x}$ abzuleiten:
$g^{'} (x) = 0,25 e^{0,25 x} - (- 0,25) e^{- 0,25 x} = 0,25 (e^{0,25 x} + e^{- 0,25 x})$
Setze $x = 0$ ein, um die Steigung an dieser Stelle zu erhalten:
$g^{'} (0)$ $=$ $0,25 (e^{0,25 \cdot 0} + e^{- 0,25 \cdot 0})$
$=$ $0,25 (e^{0} + e^{0})$
↓
Für jede Zahl gilt: $a^{0} = 1$
$=$ $0,25 (1 + 1)$
$=$ $0,5$
Fertige Tangente
Setze in $t (x) = g^{'} (0) \cdot (x - 0) + g (0)$ ein:
$t (x) = 0,5 \cdot (x - 0) + 0 = 0,5 x$
Am elegantesten geht das Aufstellen der Tangente mit der Punkt-Steigungs-Form. In jedem Fall brauchst du:
Den Funktionswert bei $x = 0$
Die Steigung bei $x = 0$ , die du durch die Ableitung $g^{'}$ ermitteln kannst.
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
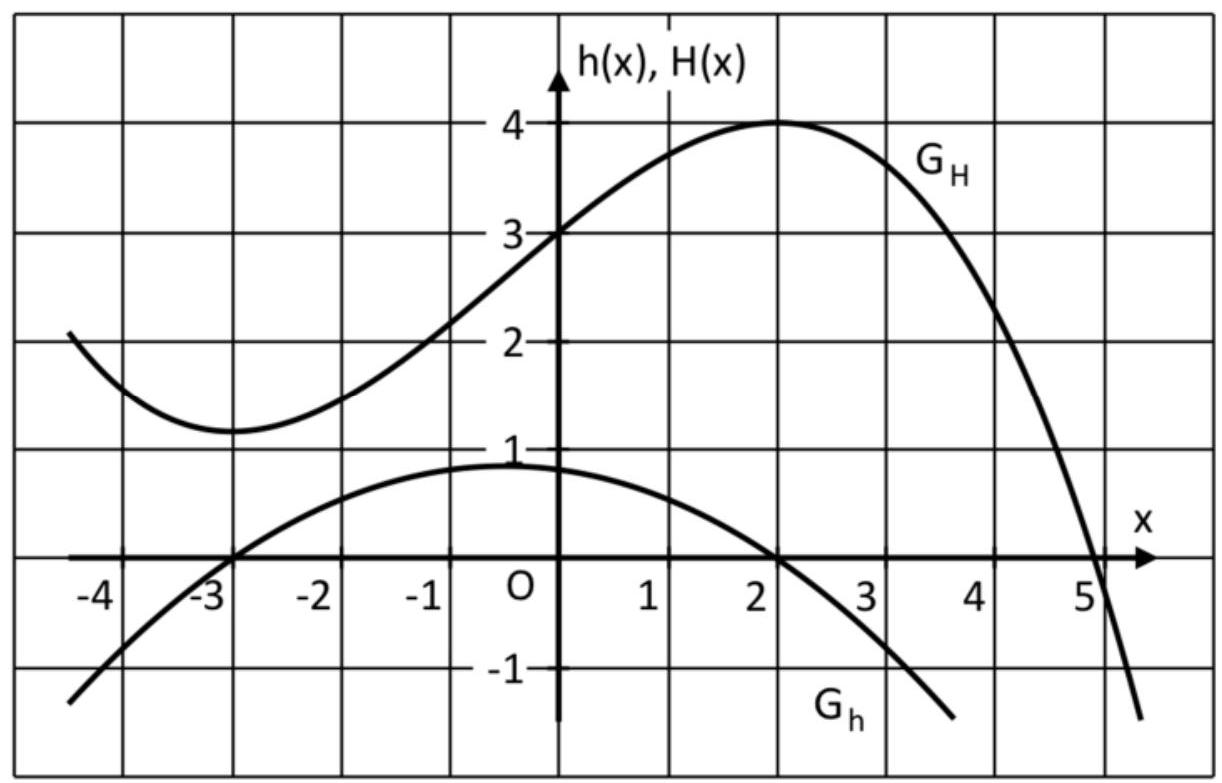
In der folgenden Abbildung ist ein Ausschnitt des Graphen der Funktion $h$ und der entsprechende Ausschnitt des Graphen einer Stammfunktion H von h dargestellt.
Entnehmen Sie der Abbildung den Wert der Differenz $H (2) - H (0)$ und interpretieren Sie diesen Wert bezüglich des Graphen von $h$ geometrisch. (3 BE)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Aus dem Graphen von $G_{H}$ kannst du direkt ablesen:
$H (2) - H (0) = 4 - 3 = 1$
Dieser Wert entspricht dem Flächeninhalt, den der Graph $G_{h}$ im Intervall $x \in [0; 2]$ mit der x-Achse einschließt.
Die Werte von $H (2)$ und $H (0)$ kannst du der Grafik entnehmen.
Überlege dir, wann du die Funktionswerte einer Stammfunktion voneinander abziehst.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$3 x^{4} - 12 x^{2}$	$=$	$0$
	↓	Klammere $3 x^{2}$ aus
$3 x^{2} (x^{2} - 4)$	$=$	$0$
	↓	Verwende die 3. binomische Formel
$3 x^{2} (x + 2) (x - 2)$	$=$	$0$

$e^{x^{2}}$	$=$	$e^{2 x - 1}$
	↓	Da die Basis (e) auf beiden Seiten gleich ist, kannst du die Exponenten vergleichen
$x^{2}$	$=$	$2 x - 1$	$- 2 x + 1$
$x^{2} - 2 x + 1$	$=$	$0$
	↓	Das ist die 2. binomische Formel
${(x - 1)}^{2}$	$=$	$0$

Setze $- x$ ein
	↓
$g (- x)$	$=$	$e^{0,25 \cdot (- x)} - e^{- 0,25 \cdot (- x)}$
	$=$	$e^{- 0,25 x} - e^{0,25 x}$
	↓	Klammere $- 1$ aus
	$=$	$- (- e^{- 0,25 x} + e^{0,25 x})$
	$=$	$- (e^{0,25 x} - e^{- 0,25 x})$
	$=$	$- g (x)$

$g^{'} (0)$	$=$	$0,25 (e^{0,25 \cdot 0} + e^{- 0,25 \cdot 0})$
	$=$	$0,25 (e^{0} + e^{0})$
	↓	Für jede Zahl gilt: $a^{0} = 1$
	$=$	$0,25 (1 + 1)$
	$=$	$0,5$

Teil 1, Analysis

Graph skizzieren

Globalverlauf

Symmetrienachweis

bestimmtes Integral

Steigung bestimmen

Fertige Tangente