Aufgaben zur Diskussion von Funktionenscharen

Wie gut kennst du dich mit Funktionenscharen aus? Vertiefe dein Wissen mit diesen gemischten Übungsaufgaben!

1
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Gegeben sind die Funktionenschar $f_{k}$ mit $f_{k} (x) = 2 kx + 3$ mit dem Parameter $k \in ℝ$ und die Parabel $p$ mit $p (x) = x^{2} - 2 x + 5$ .
Welche der Geraden $f_{k}$ ist parallel zur Tangente an $p$ im Punkt $Q (2 | 5)$ ?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente bestimmen
Berechne die Steigung der Tangente, indem du die Steigung der Parabel an dem Punkt berechnest. Bilde dazu die 1. Ableitung der Parabel.
$p ´ (x)$ $=$ $2 x - 2$
↓
Bestimme die Steigung am Punkt $(2 | 5)$
$p ´ (2)$ $=$ $4 - 2$
↓
Was heißt das für die Tangente?
$p ´ (2)$ $=$ $2$
↓
Tangente hat die Steigung 2
Parallele Gerade bestimmen
Damit die Gerade parallel zur Tangente ist, muss sie die gleiche Steigung haben.
Bestimme die Steigung der Geraden. Bilde dazu die 1. Ableitung der Geraden.
$f ´_{k} (x)$ $=$ $2 k$
↓
Diese Steigung soll gleich der der Tangente sein. Setze sie also gleich.
$2 k$ $=$ $2$ $: 2$
$k$ $=$ $1$
↓
Gib die Gerade explizit an.
$\Rightarrow f_{1} (x) = 2 x + 3$ ist die gesuchte Gerade
Graphische Darstellung
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.
Bewege den Schieberegler, bis die rote Gerade parallel zur (schwarzen) Tangente durch den Punkt $Q$ ist. Lies den Wert für $k$ und die Funktionsgleichung $f$ ab.
Vergleiche mit der rechnerischen Lösung.

Gegeben ist die Funktionenschar $f_{a}$ mit $f_{a} (x) = \frac{1}{a^{2}} x^{3} - \frac{3}{a} x^{2} - 9 x + 5 (a + 1)$ mit dem negativen Parameter $a$ .

Untersuche die Lage des Maximums.
Zeige, dass die Maxima aller Scharkurven auf einer Geraden liegen und gib deren Gleichung an.

3
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Gegeben ist die Funktionenschar $f_{k}$ mit $f_{k} (x) = \frac{kx - 2}{x^{2}}$ .
Das Schaubild zeigt den Graphen für $k = 3$ .
Bestimme die Lage des Wendepunkts in Abhängigkeit vom Parameter $k$ .
Überzeuge dich davon, dass sich für $k = 3$ die in der Abbildung gezeigte Lage des Wendepunktes ergibt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkt
$f_{k} (x) = \frac{kx - 2}{x^{2}}$
Bestimme die Ableitung.
$f_{k}^{'} (x)$ $=$ $\frac{x^{2} \cdot k - (kx - 2) \cdot 2 x}{x^{4}}$
↓
Kürze ein x und fasse dann Terme im Zähler zusammen.
$=$ $\frac{xk - 2 (kx - 2)}{x^{3}}$
$=$ $\frac{4 - kx}{x^{3}}$
Bestimme die 2. Ableitung $f_{k}^{''}$ , indem du $f_{k}^{'}$ ableitest.
$f_{k}^{''} (x)$ $=$ $\frac{x^{3} \cdot (- k) - (4 - kx) \cdot 3 x^{2}}{x^{6}}$
↓
Kürze $x^{2}$ , multipliziere aus und fasse Terme zusammen.
$=$ $\frac{2 kx - 12}{x^{4}}$
Setze die 2. Ableitung gleich Null, um Wendepunkte zu finden.
$f_{k}^{''} (x)$ $=$ $0$
$\frac{2 k x - 12}{x^{4}}$ $=$ $0$
$f_{k}^{''}$ ist Null, wenn der Zähler der Funktion Null ist.
$2 k x - 12$ $=$ $0$ $+ 12$
$2 k x$ $=$ $12$ $: 2$
$k x$ $=$ $6$
Nun benötigst du eine Fallunterscheidung, weil du nicht ohne weiteres durch $k$ teilen kannst. $k$ könnte auch Null sein und dann darfst du nicht dadurch teilen.
1. Fall: Für $k = 0$ lautet deine Gleichung am Ende $0 \cdot x = 6$ . Diese Gleichung ist für kein $x \in ℝ$ erfüllt. Also hat $f_{0}$ keine Wendestelle.
2. Fall: Wenn $k \neq 0$ ist, bekommst du nun $x = \frac{6}{k}$ als Ergebnis. $f_{k}$ hat also eine Wendestelle bei $x = \frac{6}{k}$ .
Bestimme, wo die 2. Ableitung größer bzw. kleiner 0 ist, um das Krümmungsverhalten zu ermitteln.
Wenn $k > 0$ ist:
$x < \frac{6}{k} \Rightarrow f_{k}^{^{''}} (x) < 0$
$\Rightarrow f (x)$ rechtsgekrümmt in $] - \infty; \frac{6}{k} [$
$x > \frac{6}{k} \Rightarrow f_{k}^{^{''}} (x) > 0$
$\Rightarrow f (x)$ linksgekrümmt in $] \frac{6}{k}; + \infty [$
Wenn $k < 0$ ist:
$x < \frac{6}{k} \Rightarrow f_{k}^{^{''}} (x) > 0$
$\Rightarrow f (x)$ linksgekrümmt in $] - \infty; \frac{6}{k} [$
$x > \frac{6}{k} \Rightarrow f_{k}^{‘ ‘} (x) < 0$
$\Rightarrow f (x)$ rechtsgekrümmt in $] \frac{6}{k}; + \infty [$
Krümmungsverhalten zusammenfassend
Anzahl der Wendestellen
rechtsgekrümmt in
linksgekrümmt in
k=0
keine
k>0
eine bei $x = \frac{6}{k}$
$] - \infty; \frac{6}{k} [$
$] \frac{6}{k}; + \infty [$
k<0
eine bei $x = \frac{6}{k}$
$] \frac{6}{k}; + \infty [$
$] - \infty; \frac{6}{k} [$
Überprüfung der Lösung für k=3
Überprüfe, ob der Wendepunkt für $k = 3$ übereinstimmt.
$k = 3 \Rightarrow x = \frac{6}{3} = 2$
Bestimme den y-Wert des Wendepunktes, indem du den x-Wert in f(x) einsetzt
$f_{3} (2) = \frac{3 \cdot 2 - 2}{2^{2}} = \frac{4}{4} = 1$
Gib den Wendepunkt an und überprüfe, ob er mit dem auf dem Bild übereinstimmt
Für $k = 3$ ist der Wendepunkt $(2 | 1)$
$\Rightarrow$ Stimmt mit Bild überein

	Anzahl der Wendestellen	rechtsgekrümmt in	linksgekrümmt in
k=0	keine
k>0	eine bei $x = \frac{6}{k}$	$] - \infty; \frac{6}{k} [$	$] \frac{6}{k}; + \infty [$
k<0	eine bei $x = \frac{6}{k}$	$] \frac{6}{k}; + \infty [$	$] - \infty; \frac{6}{k} [$

$f_{a} (x) = - \frac{4}{a^{2}} (8 - a) (x^{2} - ax)$ mit $a \in ℝ \ {0; 8}$

Bestimme den Flächeninhalt $A (a)$ der Fläche zwischen $G_{f_{a}}$ und der x-Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden

Nullstellen berechnen

Bestimme zuerst die Nullstellen der Funktion. Setze also die Funktion gleich 0.

$f_{a} (x)$	$=$	$0$
	↓	Setze $f_{a} (x) = - \frac{4}{a^{2}} (8 - a) (x^{2} - ax)$ ein.
$- \frac{4}{a^{2}} (8 - a) (x^{2} - ax)$	$=$	$0$	$: (- \frac{4}{a^{2}} (8 - a))$
	↓	Es wird durch alles, dass kein $x$ enthält dividiert , da dies keine Auswirkung auf die Nullstellen hat.
$x^{2} - a x$	$=$	$0$
	↓	$x$ wird ausgeklammert.
$x (x - a)$	$=$	$0$

Diese Gleichung ist dann Null, wenn entweder die Zahl vor der Klammer oder das Innere der Klammer gleich 0 ist.

$x_{1} = 0, x_{2} = a$

Integral aufstellen

Jetzt kannst du ein Integral aufstellen, um die vom Graphen $G_{f a}$ und der $x$ -Achse eingeschlossene Fläche $A (a)$ zu berechnen. Die Fläche befindet sich zwischen den beiden Nullstellen von $f_{a}$ .

$A (a)$	$=$	$\| \int_{0}^{a} - \frac{4}{a^{2}} (8 - a) (x^{2} - a x) dx \|$
	↓	Der Term $- \frac{4}{a^{2}} (8 - a)$ wird vor das Integral gezogen. Er hängt nicht von $x$ ab.
	$=$	$\| - \frac{4}{a^{2}} (8 - a) \int_{0}^{a} (x^{2} - a x) dx \|$
	↓	Bestimme eine Stammfunktion von $(x^{2} - a x)$ , um das Integral zu berechnen.
	$=$	$\| - \frac{4}{a^{2}} (8 - a) {[\frac{1}{3} x^{3} - a \frac{1}{2} x^{2}]}_{0}^{a} \|$
	↓	In die Klammer wird für $x$ die obere Grenze $(a)$ eingesetzt und minus die Klammer mit der unteren Grenze $(0)$ gerechnet.
	$=$	$\| - \frac{4}{a^{2}} (8 - a) [(\frac{1}{3} a^{3} - a \frac{1}{2} a^{2}) - (\frac{1}{3} 0^{3} - a \frac{1}{2} 0^{2})] \|$
	$=$	$\| - \frac{4}{a^{2}} (8 - a) (\frac{1}{3} a^{3} - \frac{1}{2} a^{3}) \|$
	$=$	$\| - \frac{4}{a^{2}} (8 - a) (- \frac{1}{6} a^{3}) \|$
	$=$	$\| \frac{4}{6 a^{2}} (8 a^{3} - a^{4}) \|$
	$=$	$\| \frac{2}{3} (8 a - a^{2}) \|$
	$=$	$\| \frac{2}{3} (8 a - a^{2}) \|$
	↓	Multipliziere nun die Klammer aus und sortiere nach Potenzen.
	$=$	$\| - \frac{2}{3} a^{2} + \frac{16}{3} a \|$

Um die Betragsstriche weglassen zu können und später leichter rechnen zu können, kannst du dir überlegen, wann das Innere $- \frac{2}{3} a^{2} + \frac{16}{3} a$ positiv ist und wann negativ.

$- \frac{2}{3} a^{2} + \frac{16}{3} a = - \frac{2}{3} (a^{2} - 8 a) = - \frac{2}{3} \cdot a \cdot (a - 8)$

Der Term $- \frac{2}{3} \cdot a \cdot (a - 8)$ wäre Null für $a = 0$ und $a = 8$ . Somit schaust du dir die folgenden Bereiche an:

$a < 0$
$0 < a < 8$ und
$a > 8$

In einer Vorzeichentabelle siehst du, wann $- \frac{2}{3} \cdot a \cdot (a - 8)$ positiv ist und wann negativ:

	$a < 0$	$0 < a < 8$	$a > 8$
$- \frac{2}{3}$	$-$	$-$	$-$
$a$	$-$	$+$	$+$
$a - 8$	$-$	$-$	$+$

$- \frac{2}{3} \cdot a \cdot (8 - a)$	$-$	$+$	$-$

$\Rightarrow - \frac{2}{3} a^{2} + \frac{16}{3} > 0$ für $0 < a < 8$ und sonst ist $- \frac{2}{3} a^{2} + \frac{16}{3} < 0$

Antwort: $A (a) = {\begin{matrix} - \frac{2}{3} a^{2} + \frac{16}{3} a & 0 < a < 8 \\ \frac{2}{3} a^{2} - \frac{16}{3} a & sonst \end{matrix}$

Für welche $a$ ist der Inhalt der Fläche $A (a)$ gleich 8?

Bestimme für $0 < a < 8$ den Flächeninhalt $A (a)$ so, dass dieser möglichst groß wird. Gib den maximalen Flächeninhalt an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Maximum
Der Maximalwert der Fläche ist das gleiche, wie das Maximum der Funktion .
Um dieses zu bestimmen, muss $A_{1} (a)$ ( $A_{1} = - \frac{2}{3} a^{2} + \frac{16}{3} a$ ) abgeleitet werden.
$A_{1}^{'} (a) = - \frac{4}{3} a + \frac{16}{3}$
Der Graph von $A_{1} (a)$ ist eine nach unten geöffnete Parabel, d.h. es gibt nur ein Maximum. Das gesuchte Maximum ist die Nullstelle der Ableitung, demnach wird $\frac{dA}{da}$ gleich $0$ gesetzt.
$0$ $=$ $A_{1}^{'} (a)$
$0$ $=$ $- \frac{4}{3} a + \frac{16}{3}$ $+ \frac{4}{3} a$
$\frac{4}{3} a$ $=$ $\frac{16}{3}$ $: \frac{4}{3}$
$a$ $=$ $4$
Die Bedingung in der Aufgabenstellung $0 < a < 8$ ist für $a = 4$ erfüllt.
Die Stelle, an der $A_{1} (a)$ den größten Wert hat ist bekannt, wie hoch dieser ist wird ermittelt, indem das berechnete $a$ in $A_{1} (a)$ eingesetzt wird.
$A_{1} (4)$ $=$ $- \frac{2}{3} \cdot 4^{2} + \frac{16}{3} \cdot 4$
$=$ $- \frac{2}{3} \cdot 16 + \frac{16}{3} \cdot 4$
$=$ $- \frac{32}{3} + \frac{64}{3}$
$=$ $\frac{32}{3}$
$=$ $10, 6$
Antwort: Der maximale Flächeninhalt beträgt $\frac{32}{3}$ FE.

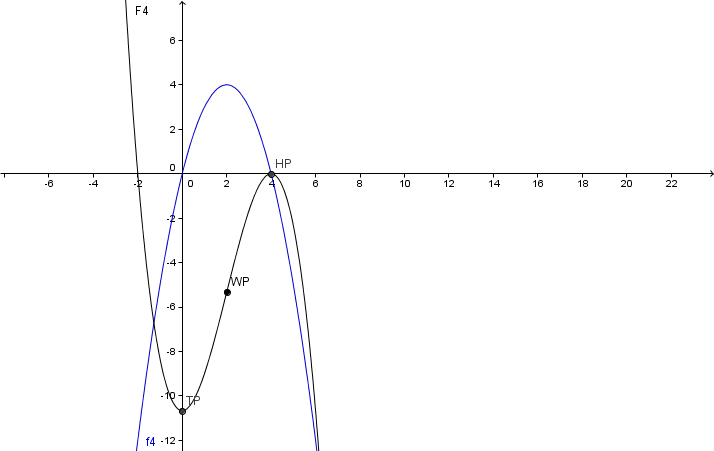
$F_{4} (x) = \int_{4}^{x} f_{4} (t) dt$ Bestimme den Term $F_{4} (x)$ und alle Nullstellen von $F_{4}$

Berechne die Hoch-, Tief- und Wendepunkte von $G_{F_{4}}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema
Leite $F_{4} (x) = - \frac{1}{3} x^{3} + 2 x^{2} - \frac{32}{3}$ zweimal ab.
$F_{4}^{'} (x) = - x^{2} + 4 x$
$F_{4}^{''} (x) = - 2 x + 4$
Extrema bestimmen
Bestimme die Extrema von $F_{4} (x)$ .
$F_{4}^{'} {(x)}_{}$ $=$ $0$
↓
Setze $F_{4}^{'} (x) = - x^{2} + 4 x$ ein.
$- x^{2} + 4 x$ $=$ $0$
↓
Klammere $- x$ aus.
$- x (x - 4)$ $=$ $0$
Die Gleichung ist gleich 0, wenn ein Element der Multiplikation ( $- x \cdot (x - 4)$ ) Null ist.
$- x = 0$ für $x = 0$
$x - 4 = 0$ für $x = 4$
$x_{1} = 0, x_{2} = 4$
Extremum für $x = 0$
Setze die gefundene Nullstelle $x = 0$ der Ableitung von $F_{4} (x)$ in $F_{4} (x)$ ein.
$F_{4} (x) = - \frac{1}{3} x^{3} + 2 x^{2} - \frac{32}{3}$
$F_{4} (0) = - \frac{1}{3} \cdot 0^{3} + 2 \cdot 0^{2} - \frac{32}{3} = - \frac{32}{3}$
Setze jetzt $x = 0$ in $F_{4}^{''} (x) = - 2 x + 4$ ein.
$F_{4}^{''} (0) = - 2 \cdot 0 + 4 = 4$
Da $F_{4}^{''} (0) > 0$ ist, hat $F_{4} (x)$ an der Stelle $x_{1} = 0$ einen Tiefpunkt $TP (0 | - \frac{32}{3})$ .
Extremum für $x = 4$
Setze die gefundene Nullstelle $x = 4$ der Ableitung von $F_{4} (x)$ in $F_{4} (x)$ ein.
$F_{4} (x) = - \frac{1}{3} x^{3} + 2 x^{2} - \frac{32}{3}$
$F_{4} (4) = - \frac{1}{3} \cdot 4^{3} + 2 \cdot 4^{2} - \frac{32}{3} = 0$
Setze jetzt $x = 4$ in $F_{4}^{''} (x) = - 2 x + 4$ ein.
$F_{4}^{''} (4) = - 2 \cdot 4 + 4 = - 4$
Da $F_{4}^{''} (4) < 0$ ist, hat $F_{4} (x)$ an der Stelle $x_{2} = 4$ einen Hochpunkt $HP (4 | 0)$
Wendepunkt bestimmen
Bestimme nun den Wendepunkt.
Setze dafür die zweite Ableitung $F_{4}^{''} (x) = - 2 x + 4$ gleich $0$ .
$0$ $=$ $F_{4}^{''} (x)$
$0$ $=$ $- 2 x + 4$ $+ 2 x$
$2 x$ $=$ $4$ $: 2$
$x$ $=$ $2$
Setze $x = 2$ in $F_{4} (x)$ ein.
$F_{4} (2) = - \frac{1}{3} \cdot 2^{3} + 2 \cdot 2^{2} - \frac{32}{3} = - \frac{16}{3}$
Damit ergeben sich die Koordinaten des Wendepunktes $W P (2 | - \frac{16}{3})$ .
Skizziere $G_{f_{4}}$ und $G_{F_{4}}$ im selben Koordinatensystem.

5
Gegeben ist die Funktionenschar mit dem Parameter $a \in ℝ$ durch $f_{a} (x) = \frac{- 2 x^{2} + 50}{x^{2} + a}$
Untersuche $f_{a}$ auf Definitionsbereich und Nullstellen. Gib den Schnittpunkt $Y_{a}$ mit der y-Achse an

Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsbereich bestimmen
Finde Definitionslücken, indem du schaust, wann der Nenner Null wird.
$x^{2} + a = 0$ $| - a$
$x^{2} = - a$
Mache eine Fallunterscheidung für a.
$a > 0$ : Gleichung nie erfüllt
Bestimme den Definitionsbereich.
$\Rightarrow D_{f_{a}} = ℝ$
$a \leq 0 :$ $x = \pm \sqrt{- a}$
Bestimme den Definitionsbereich.
$\Rightarrow D_{f_{a}} = ℝ \ {\pm \sqrt{- a}}$
Nullstellen bestimmen
$- 2 x^{2} + 50 = 0 | - 50$
$- 2 x^{2} = - 50$ $| : (- 2)$
$x^{2} = 25$ $| \sqrt{}$
$x = \pm 5$
Gib die beiden Nullstellen an.
$\Rightarrow x_{1} = - 5, x_{2} = 5$
Y-Achsenabschnitt bestimmen
Setze $0$ in die Funktion ein
$f_{a} (0) = \frac{- 2 \cdot {(0)}^{2} + 50}{{(0)}^{2} + a} = \frac{50}{a}$
Gib den Schnittpunkt an.
$\Rightarrow Y_{a} (0 | \frac{50}{a})$

Berechne $\lim_{x \to \sqrt{- a} \pm 0} f (x)$ , sofern $a \leq 0$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Grenzwert berechnen
$f_{a} (x)$ $=$ $\frac{- 2 x^{2} + 50}{x^{2} + a}$
↓
Faktorisiere die Funktion für $a \leq 0$
$=$ $\frac{- 2 (x + 5) (x - 5)}{(x + \sqrt{- a}) (x - \sqrt{- a})}$
Berechne nun den Grenzwert
$\lim_{x \to \sqrt{- a} \pm 0} f_{a} (x)$ $=$ $\lim_{x \to \sqrt{- a} \pm 0} \frac{- 2 (x + 5) (x - 5)}{(x + \sqrt{- a}) (x - \sqrt{- a})}$
↓
Setze die Grenze ein.
$=$ $\frac{- 2 (\sqrt{- a} + 5) (\sqrt{- a} - 5)}{(\sqrt{- a} + \sqrt{- a}) \underset{_{- 0 \Rightarrow 0}}{\underset{⏟}{(\sqrt{- a} - \sqrt{- a})}}}$
Bestimme nun den Grenzwert. Je nachdem von welcher Seite man sich $\sqrt{- a}$ nähert, erhält man entweder ein $+$ oder ein $-$ als Vorzeichen:
$\overset{}{\to}$

Fertige eine Skizze der Funktionsgraphen für $a = - 25, a = - 16$ und $a = 25$ an.

$f_{a} (x) = \frac{- 2 x^{2} + 50}{x^{2} + a}$
Setze die geforderten Werte für a ein und bestimme so die 3 Funktionsterme
$f_{- 25} (x) = \frac{- 2 x^{2} + 50}{x^{2} - 25} \frac{- 2 (x^{2} - 25)}{(x^{2} - 25)} - 2$
Beachte hier aber die Definitionslücken beim Einzeichnen!
$f_{- 16} (x) = \frac{- 2 x^{2} + 50}{x^{2} - 16}$
$f_{25} (x) = \frac{- 2 x^{2} + 50}{x^{2} + 25}$
Skizze:
6
Für jedes $a \in ℝ \ {0}$ ist die Funktionenschar gegeben durch $f_{a} (x) = x \cdot e^{a x} + \frac{3}{a}$ .
Der Graph der Funktion ist $K_{a}$ .
Gib bei allen Teilaufgaben die Ergebnisse in Abhängigkeit vom Scharparameter $a$ an.
Wo schneiden die Scharkurven die $y$ -Achse?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Die $y$ -Achse wird für $x = 0$ geschnitten.
Setze $x = 0$ in die Funktionsgleichung ein:
$f_{a} (0) = 0 \cdot e^{a \cdot 0} + \frac{3}{a} = 0 \cdot 1 + \frac{3}{a} = \frac{3}{a}$
Antwort: Der Schnittpunkt der Scharkurven mit der $y$ -Achse hat die Koordinaten $S_{y} (0 | \frac{3}{a})$ .

Untersuche $K_{a}$ auf Hoch- und Tiefpunkte.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Die notwendige Bedingung für ein Extremum lautet: $f_{a}^{'} (x) = 0$
Berechne die 1. Ableitung, beachte dabei die Produktregel und die Kettenregel:
$f_{a}^{'} (x) = 1 \cdot e^{a x} + x \cdot e^{a x} \cdot a = (1 + a \cdot x) \cdot e^{a x}$
Setze $f_{a}^{'} (x) = 0$
$\Rightarrow 0 = \underset{= 0}{\underset{⏟}{(1 + a \cdot x)}} \cdot \underset{immer > 0}{\underset{⏟}{e^{a \cdot x}}}$
Nur die Klammer kann null werden:
$0 = 1 + a \cdot x \Rightarrow x = - \frac{1}{a}$
Die Feststellung, ob sich an der Stelle $x = - \frac{1}{a}$ ein Extremum befindet, kann mit einer Monotonietabelle oder der 2. Ableitung erfolgen. Hier erfolgt die Überprüfung mit der 2. Ableitung:
Ist $f_{a}^{''} (x) > 0$ , dann hat die Scharkurve $K_{a}$ an der Stelle $x$ einen Tiefpunkt.
Ist $f_{a}^{''} (x) < 0$ , dann hat die Scharkurve $K_{a}$ an der Stelle $x$ einen Hochpunkt.
Berechne die 2. Ableitung, beachte dabei wieder die Produktregel und die Kettenregel:
$f_{a}^{'} (x) = (1 + a \cdot x) \cdot e^{a x}$
$f_{a}^{''} (x) = a \cdot e^{a x} + (1 + a \cdot x) \cdot e^{a x} \cdot a = (a^{2} \cdot x + 2 a) \cdot e^{a x}$
Setze $x = - \frac{1}{a}$ in $f_{a}^{''} (x) = (a^{2} \cdot x + 2 a) \cdot e^{a x}$ ein:
$f_{a}^{''} (- \frac{1}{a}) = (a^{2} \cdot (- \frac{1}{a}) + 2 a) \cdot e^{a \cdot (- \frac{1}{a})} = (- a + 2 a) \cdot e^{- 1} = a \cdot e^{- 1}$
Das Ergebnis ist vom Scharparameter $a$ abhängig, d.h. es ist eine Fallunterscheidung bzgl. des Vorzeichens von $a$ erforderlich.
Fallunterscheidung
Fall 1: $a > 0$
$f_{a}^{''} (- \frac{1}{a}) = a \cdot e^{- 1} > 0 \Rightarrow TP$
Fall 2: $a < 0$
$f_{a}^{''} (- \frac{1}{a}) = a \cdot e^{- 1} < 0 \Rightarrow HP$
Setze $x = - \frac{1}{a}$ in $f_{a} (x)$ ein, um die $y$ -Koordinate der Extrema zu berechnen.
$f_{a} (- \frac{1}{a}) = (- \frac{1}{a}) \cdot e^{a \cdot (- \frac{1}{a})} + \frac{3}{a} = \frac{3}{a} - \frac{1}{a} \cdot e^{- 1} = \frac{1}{a} \cdot (3 - e^{- 1})$
Antwort: Für $a > 0$ hat der Tiefpunkt die Koordinaten $T P (- \frac{1}{a} | \frac{1}{a} \cdot (3 - e^{- 1}))$ und für $a < 0$ hat der Hochpunkt die Koordinaten $H P (- \frac{1}{a} | \frac{1}{a} \cdot (3 - e^{- 1}))$ .

Bestimme das Verhalten der Funktion $f_{a} (x)$ für $x \to - \infty$ und für $x \to \infty$ und gib gegebenenfalls die Asymptote an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Betrachte zunächst $\lim_{x \to + \infty} (x \cdot e^{a x} + \frac{3}{a})$ . Wie verhält sich der Ausdruck $x \cdot e^{a x}$ , wenn $x$ sehr groß wird? Das Verhalten hängt vom Vorzeichen des Scharparameters $a$ ab, d.h. es ist eine Fallunterscheidung bzgl. des Vorzeichens von $a$ erforderlich.
Fallunterscheidung
Fall 1: $a > 0$
$\lim_{x \to + \infty} (x \cdot e^{a x} + \frac{3}{a}) = \lim_{x \to + \infty} \underset{\to + \infty}{\underset{⏟}{x \cdot e^{a x}}} + \frac{3}{a} = + \infty$
Für $a > 0$ wächst $e^{a x}$ für $x \to + \infty$ stärker als jede Potenz von $x$ . Der Ausdruck $x \cdot e^{a x}$ geht somit gegen $+ \infty$ .
$\lim_{x \to - \infty} (x \cdot e^{a x} + \frac{3}{a}) = \lim_{x \to - \infty} \underset{\to 0}{\underset{⏟}{x \cdot e^{a x}}} + \frac{3}{a} = \frac{3}{a}$
Für $a > 0$ geht $e^{a x}$ für $x \to - \infty$ stärker gegen $0$ als $x \to - \infty$ . Der Ausdruck $x \cdot e^{a x}$ geht somit gegen $0$ .
Fall 2: $a < 0$
$\lim_{x \to + \infty} (x \cdot e^{a x} + \frac{3}{a}) = \lim_{x \to + \infty} \underset{\to 0}{\underset{⏟}{x \cdot e^{a x}}} + \frac{3}{a} = \frac{3}{a}$
Für $a < 0$ geht $e^{a x}$ für $x \to + \infty$ stärker gegen $0$ als $x \to + \infty$ . Der Ausdruck $x \cdot e^{a x}$ geht somit gegen $0$ .
$\lim_{x \to - \infty} (x \cdot e^{a x} + \frac{3}{a}) = \lim_{x \to - \infty} \underset{\to - \infty}{\underset{⏟}{x \cdot e^{a x}}} + \frac{3}{a} = - \infty$
Für $a < 0$ wächst $e^{a x}$ für $x \to - \infty$ stärker als jede Potenz von $x$ . Der Ausdruck $x \cdot e^{a x}$ geht somit gegen $- \infty$ .
Alle Scharkurven haben eine waagrechte Asymptote $y_{A} = \frac{3}{a}$ .

Skizziere für $a = - 3$ und $a = 1$ die Graphen von $K_{- 3}$ und von $K_{1}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Für $a = - 3$ lautet $f_{- 3} (x) = x \cdot e^{- 3 x} - 1$ und für $a = 1$ ist $f_{1} = x \cdot e^{x} + 3$ . Bekannt sind weiterhin der Schnittpunkt mit der y-Achse $S_{y} (0 | \frac{3}{a})$ , der Extrempunkt $E (- \frac{1}{a} | \frac{1}{a} \cdot (3 - e^{- 1}))$ und die waagrechte Asymptote $y_{A} = \frac{3}{a}$ . Zum Skizzieren der beiden Graphen ist es sinnvoll, noch einige Funktionswerte zu berechnen. Sie sind in den beiden folgenden Tabellen aufgelistet.
Tabelle für $f_{- 3} (x) = x \cdot e^{- 3 x} - 1$ :
x
$f_{- 3} (x)$
besonderer Punkt
-0,5
-3,24
0
-1
$S_{y}$
0,33
-0,88
HP
1
-0,95
3
-1
Die Funktion $f_{- 3} (x) = x \cdot e^{- 3 x} - 1$ hat die waagrechte Asymptote $y_{A} = - 1$ .
Tabelle für $f_{1} = x \cdot e^{x} + 3$ :
x
$f_{1} (x)$
besonderer Punkt
-3
2,85
-2
2,73
-1
2,63
TP
0
3
$S_{y}$
0,5
3,82
1
5,72
Die Funktion $f_{1} (x) = x \cdot e^{x} + 3$ hat die waagrechte Asymptote $y_{A} = 3$ .
Die Graphen von $K_{- 3}$ und von $K_{1}$ .

Welche Scharkurve hat für $x = \frac{1}{2}$ ein Extremum?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Ein Extremum liegt vor, wenn $f_{a}^{'} (x) = 0$ ist.
Im Aufgabenteil b) wurde $f_{a}^{'} (x)$ berechnet: $f_{a}^{'} (x) = (1 + a \cdot x) \cdot e^{a x}$
Setze den Wert $x = \frac{1}{2}$ in die $1.$ Ableitung ein:
$f_{a}^{'} (\frac{1}{2}) = e^{a \cdot \frac{1}{2}} \cdot (1 + a \cdot \frac{1}{2})$
Setze $f_{a}^{'} (\frac{1}{2}) = 0$
$\Rightarrow 0 = \underset{immer > 0}{\underset{⏟}{e^{a \cdot \frac{1}{2}}}} \cdot \underset{= 0}{\underset{⏟}{(1 + a \cdot \frac{1}{2})}}$
Nur die Klammer kann null werden:
$0 = 1 + a \cdot \frac{1}{2} \Rightarrow a = - 2$
Antwort: Für $a = - 2$ hat die Scharfunktion $f_{- 2} (x) = x \cdot e^{- 2 x} - \frac{3}{2}$ an der Stelle $x = \frac{1}{2}$ ein Extremum.

Auf welcher Ortskurve liegen die Extrema?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ortskurve
Für die Ortskurve der Extrema benötigst du die Extrempunktkoordinaten.
Das Extremum hat die Koordinaten $E (- \frac{1}{a} | \frac{1}{a} \cdot (3 - e^{- 1}))$ .
Für die Berechnung der Ortskurve setzt du $x = - \frac{1}{a}$ und $y = \frac{1}{a} \cdot (3 - e^{- 1})$ .
Löse dann $x = - \frac{1}{a}$ nach $a$ auf $\Rightarrow a = - \frac{1}{x}$ .
Setze $a = - \frac{1}{x}$ in $y = \frac{1}{a} \cdot (3 - e^{- 1})$ ein:
$y = \frac{1}{- \frac{1}{x}} \cdot (3 - e^{- 1}) = - x \cdot (3 - e^{- 1}) = (e^{- 1} - 3) \cdot x$
Antwort: Die Gleichung der Ortskurve lautet $y = (e^{- 1} - 3) \cdot x$ . Der Graph der Ortskurve ist eine Ursprungsgerade mit der Steigung $m = e^{- 1} - 3 \approx - 2,63$ .
Zur Veranschaulichung sind im folgenden Applet mehrere Scharkurven und die Ortskurve der Extrema dargestellt.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.

x	$f_{- 3} (x)$	besonderer Punkt
-0,5	-3,24
0	-1	$S_{y}$
0,33	-0,88	HP
1	-0,95
3	-1

x	$f_{1} (x)$	besonderer Punkt
-3	2,85
-2	2,73
-1	2,63	TP
0	3	$S_{y}$
0,5	3,82
1	5,72

Für jedes $a \in ℝ \ {0}$ ist die Funktionenschar gegeben durch $f_{a} (x) = x + a \cdot e^{- x} + \frac{1}{a}$ .

Der Graph der Funktion ist $K_{a}$ .

Gib bei allen Teilaufgaben die Ergebnisse in Abhängigkeit vom Scharparameter $a$ an.

Wo schneiden die Scharkurven die $y$ -Achse?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Die $y$ -Achse wird für $x = 0$ geschnitten.
Setze $x = 0$ in die Funktionsgleichung ein:
$f_{a} (0) = 0 + a \cdot e^{- 0} + \frac{1}{a} = a \cdot 1 + \frac{1}{a}$
Antwort: Die y-Achse wird im Punkt $S_{y} (0 | a + \frac{1}{a})$ geschnitten.

Welche Scharkurve schneidet die $y$ -Achse im Punkt $S_{y} (0 | 5,2)$ ?

Untersuche $K_{a}$ auf Hoch- und Tiefpunkte.

Welche Scharkurve hat für $x = 0$ die Steigung $\frac{1}{3}$ ?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Die Steigung für $x = 0$ soll $\frac{1}{3}$ sein.
Setze $x = 0$ in $f_{a}^{'} (x) = 1 - a \cdot e^{- x}$ ein:
$f_{a}^{'} (0) = 1 - a \cdot e^{- 0} = 1 - a$
Setze $f_{a}^{'} (0) = \frac{1}{3} \Rightarrow$ $1 - a = \frac{1}{3} \Rightarrow a = \frac{2}{3}$
Antwort: Die Scharkurve $K_{\frac{2}{3}}$ hat bei $x = 0$ die Steigung $\frac{1}{3}$ .
Bestimme das Verhalten der Funktion $f_{a} (x)$ für $x \to - \infty$ und für $x \to \infty$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Betrachte zunächst $\lim_{x \to + \infty} (x + a \cdot e^{- x} + \frac{1}{a})$ . Wie verhält sich der Ausdruck $a \cdot e^{- x}$ , wenn $x$ sehr groß wird? Das Verhalten hängt vom Vorzeichen des Scharparameters $a$ ab, d.h. es ist eine Fallunterscheidung bzgl. des Vorzeichens von $a$ erforderlich.
Fallunterscheidung
Fall 1: $a > 0$
$\lim_{x \to + \infty} (x + a \cdot e^{- x} + \frac{1}{a}) = \lim_{x \to + \infty} (x + \underset{\to 0}{\underset{⏟}{a \cdot e^{- x}}} + \frac{1}{a}) = \lim_{x \to + \infty} (x + \frac{1}{a})$
$\Rightarrow y_{A s y m p t o t e} = x + \frac{1}{a}$ ist eine schiefe Asymptote (im Weiteren abgekürzt mit $y_{A}$ )
$\lim_{x \to - \infty} (x + a \cdot e^{- x} + \frac{1}{a}) = \lim_{x \to - \infty} (x + \underset{\to + \infty}{\underset{⏟}{a \cdot e^{- x}}} + \frac{1}{a}) = + \infty$
Fall 2: $a < 0$
$\lim_{x \to + \infty} (x + a \cdot e^{- x} + \frac{1}{a}) = \lim_{x \to + \infty} (x + \underset{\to 0}{\underset{⏟}{a \cdot e^{- x}}} + \frac{1}{a}) = \lim_{x \to + \infty} (x + \frac{1}{a})$
$\Rightarrow y_{A} = x + \frac{1}{a}$ ist eine schiefe Asymptote.
$\lim_{x \to - \infty} (x + a \cdot e^{- x} + \frac{1}{a}) = \lim_{x \to - \infty} (x + \underset{\to - \infty}{\underset{⏟}{a \cdot e^{- x}}} + \frac{1}{a}) = - \infty$
Alle Scharkurven haben bei $+ \infty$ eine schiefe Asymptote $y_{A} = x + \frac{1}{a}$ .
Skizziere für $a = - 1$ und $a = 1$ die Graphen von $K_{- 1}$ und von $K_{1}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kurvendiskussion
Für $a = - 1$ lautet $f_{- 1} (x) = x - e^{- x} - 1$ und für $a = 1$ ist $f_{1} = x + e^{- x} + 1$ .
Bekannt sind weiterhin der Schnittpunkt mit der y-Achse $S_{y} (0 | a + \frac{1}{a})$ , der Tiefpunkt $T P (\ln (a) | \ln (a) + 1 + \frac{1}{a})$ und die schiefe Asymptote $y_{A} = x + \frac{1}{a}$ .
Zum Skizzieren der beiden Graphen ist es sinnvoll, noch einige Funktionswerte zu berechnen. Sie sind in den beiden folgenden Tabellen aufgelistet.
Tabelle für $f_{- 1} (x) = x - e^{- x} - 1$
x
$f_{- 1} (x)$
besonderer Punkt
-1
-4,72
-0,5
-3,15
0
-2
$S_{y}$
0,5
-1,11
1
-0,37
2
0,86
3
1,95
4
2,98
Die Funktion $f_{- 1} (x) = x - e^{- x} - 1$ hat die schiefe Asymptote $y_{A} = x - 1$ .
Tabelle für $f_{1} = x + e^{- x} + 1$
x
$f_{1} (x)$
besonderer Punkt
-2
6,39
-1
2,72
0
2
$S_{y}$ und TP
0,5
2,11
1
2,37
2
3,14
3
4,04
4
5,02
Die Funktion $f_{1} = x + e^{- x} + 1$ hat die schiefe Asymptote $y_{A} = x + 1$ .
Graphen von $K_{- 1}$ und von $K_{1}$ .
Auf welcher Ortskurve $g (x)$ liegen die Extrema?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ortskurve
Für die Ortskurve der Tiefpunkte benötigst du die Tiefpunktkoordinaten:
$T P (\ln (a) | \ln (a) + 1 + \frac{1}{a})$ .
Für die Berechnung der Ortskurve setzt du $x = \ln (a)$ und $y = \ln (a) + 1 + \frac{1}{a}$ .
Löse dann $x = \ln (a)$ nach $a$ auf $\Rightarrow a = e^{x}$ .
Setze $a = e^{x}$ in $y = \ln (a) + 1 + \frac{1}{a}$ ein:
$y = \ln (e^{x}) + 1 + \frac{1}{e^{x}} = x + 1 + e^{- x}$
Antwort: Die Gleichung der Ortskurve lautet $g (x) = x + 1 + e^{- x}$ .
Zur Veranschaulichung sind im folgenden Applet mehrere Scharkurven und die Ortskurve der Tiefpunkte dargestellt.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.
Anmerkung: Die Scharkurve $K_{1}$ und die Ortskurve sind identisch.

x	$f_{- 1} (x)$	besonderer Punkt
-1	-4,72
-0,5	-3,15
0	-2	$S_{y}$
0,5	-1,11
1	-0,37
2	0,86
3	1,95
4	2,98

x	$f_{1} (x)$	besonderer Punkt
-2	6,39
-1	2,72
0	2	$S_{y}$ und TP
0,5	2,11
1	2,37
2	3,14
3	4,04
4	5,02

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$8$	$=$	$A (a)$
	↓	Setze $A_{1} = - \frac{2}{3} a^{2} + \frac{16}{3} a$ ein.
$8$	$=$	$- \frac{2}{3} a^{2} + \frac{16}{3} a$	$- 8$
$0$	$=$	$- \frac{2}{3} a^{2} + \frac{16}{3} a - 8$
	↓	Wende die Mitternachtsformel an.
$a_{1,2}$	$=$	$\frac{- \frac{16}{3} \pm \sqrt{{(\frac{16}{3})}^{2} - 4 (- \frac{2}{3}) (- 8)}}{2 (- \frac{2}{3})}$
	↓	Multipliziere unter der Wurzel aus.
$a_{1,2}$	$=$	$\frac{- \frac{16}{3} \pm \sqrt{\frac{256}{9} - \frac{64}{3}}}{2 (- \frac{2}{3})}$
	↓	Fasse zusammen.
$a_{1,2}$	$=$	$\frac{- \frac{16}{3} \pm \sqrt{\frac{64}{9}}}{- \frac{4}{3}}$
$a_{1,2}$	$=$	$\frac{- \frac{16}{3} \pm \frac{8}{3}}{- \frac{4}{3}}$
$a_{1,2}$	$=$	$- \frac{3}{4} (- \frac{16}{3} \pm \frac{8}{3})$
$a_{1,2}$	$=$	$4 \mp 2$

$8$	$=$	$A (a)$
	↓	Setze $A_{2} = \frac{2}{3} a^{2} - \frac{16}{3} a$ ein.
$8$	$=$	$\frac{2}{3} a^{2} - \frac{16}{3} a$	$- 8$
$0$	$=$	$\frac{2}{3} a^{2} - \frac{16}{3} a - 8$
	↓	Wende die Mitternachtsformel an.
$a_{3,4}$	$=$	$\frac{\frac{16}{3} \pm \sqrt{{(\frac{16}{3})}^{2} - 4 (\frac{2}{3}) (- 8)}}{2 (\frac{2}{3})}$
	↓	Multipliziere unter der Wurzel aus.
$a_{3,4}$	$=$	$\frac{\frac{16}{3} \pm \sqrt{\frac{256}{9} + \frac{64}{3}}}{2 (\frac{2}{3})}$
	↓	Fasse zusammen.
$a_{3,4}$	$=$	$\frac{\frac{16}{3} \pm \sqrt{\frac{448}{9}}}{\frac{4}{3}}$
$a_{3,4}$	$=$	$\frac{3}{4} (\frac{16}{3} \pm \frac{8 \sqrt{7}}{3})$
$a_{3,4}$	$=$	$4 \pm 2 \sqrt{7}$

$f_{4} (t)$	$=$	$\int_{4}^{x} f_{4} (t) dt$
	$=$	$\int_{4}^{x} (- t^{2} + 4 t) dt$
	↓	Integriere.
	$=$	${[- \frac{1}{3} t^{3} + \frac{4}{2} t^{2}]}_{4}^{x}$
	↓	In die Klammer wird für $t$ die obere Grenze $(x)$ eingesetzt und minus die Klammer mit der unteren Grenze $(4)$ gerechnet.
	$=$	$[- \frac{1}{3} x^{3} + \frac{4}{2} x^{2}] - [- \frac{1}{3} 4^{3} + \frac{4}{2} 4^{2}]$
	$=$	$- \frac{1}{3} x^{3} + \frac{4}{2} x^{2} + \frac{64}{3} - 32$
	$=$	$- \frac{1}{3} x^{3} + 2 x^{2} - \frac{32}{3}$

$0$	$=$	$x^{2} - 8 x + 16$
$x_{2,3}$	$=$	$\frac{8 \pm \sqrt{{(8)}^{2} - 4 \cdot (1) \cdot (16)}}{2 \cdot (1)}$
$x_{2,3}$	$=$	$\frac{8 \pm \sqrt{(64 - 64)}}{2}$
$x_{2,3}$	$=$	$\frac{8}{2}$
$x_{2,3}$	$=$	$4$

$5,2$	$=$	$a + \frac{1}{a}$	$\cdot a$
$5,2 a$	$=$	$a^{2} + 1$	$- 5,2 a$
$0$	$=$	$a^{2} - 5,2 a + 1$
	↓	Löse mit der pq-Formel.
$a_{1,2}$	$=$	$- \frac{p}{2} \pm \sqrt{{(\frac{p}{2})}^{2} - q}$
	↓	Setze $p = - 5,2$ und $q = 1$ ein.
	$=$	$- \frac{(- 5,2)}{2} \pm \sqrt{{(\frac{- 5,2}{2})}^{2} - 1}$
	↓	Vereinfache.
	$=$	$2,6 \pm \sqrt{{2,6}^{2} - 1}$
	$=$	$2,6 \pm \sqrt{5,76}$
	$=$	$2,6 \pm 2,4$
$a_{1}$	$=$	$5$
$a_{2}$	$=$	$0,2$

Aufgaben zur Diskussion von Funktionenscharen

Graphische Darstellung

2 Gerade bestimmen, auf der alle Maxima liegen

Krümmungsverhalten zusammenfassend

Überprüfung der Lösung für k=3

Nullstellen berechnen

Integral aufstellen

Alternativer Rechenweg für die Nullstelle

Extrema bestimmen

Extremum für $x = 0$

Extremum für $x = 4$

Wendepunkt bestimmen

Nullstellen bestimmen

Y-Achsenabschnitt bestimmen

Skizze:

Fallunterscheidung

Fallunterscheidung

$\lim_{x \to - \infty} (x \cdot e^{a x} + \frac{3}{a}) = \lim_{x \to - \infty} \underset{\to 0}{\underset{⏟}{x \cdot e^{a x}}} + \frac{3}{a} = \frac{3}{a}$

Tabelle für $f_{- 3} (x) = x \cdot e^{- 3 x} - 1$ :

Tabelle für $f_{1} = x \cdot e^{x} + 3$ :

Die Graphen von $K_{- 3}$ und von $K_{1}$ .

Fallunterscheidung

Tabelle für $f_{- 1} (x) = x - e^{- x} - 1$

Tabelle für $f_{1} = x + e^{- x} + 1$

Graphen von $K_{- 1}$ und von $K_{1}$ .

$p ´ (x)$	$=$	$2 x - 2$
	↓	Bestimme die Steigung am Punkt $(2 \| 5)$
$p ´ (2)$	$=$	$4 - 2$
	↓	Was heißt das für die Tangente?
$p ´ (2)$	$=$	$2$
	↓	Tangente hat die Steigung 2

$f ´_{k} (x)$	$=$	$2 k$
	↓	Diese Steigung soll gleich der der Tangente sein. Setze sie also gleich.
$2 k$	$=$	$2$	$: 2$
$k$	$=$	$1$
	↓	Gib die Gerade explizit an.

$f ´_{a} (x)$	$=$	$\frac{1}{a^{2}} \cdot 3 x^{2} - \frac{3}{a} \cdot 2 x - 9$
	$=$	$\frac{3}{a^{2}} x^{2} - \frac{6}{a} x - 9$
	↓	Setze die 1.Ableitung gleich Null, um Extremstellen zu bestimmen.
$\frac{3}{a^{2}} x^{2} - \frac{6}{a} x - 9$	$=$	$0$
	↓	Wende die Mitternachtsformel an.
	$=$

	$=$	$(\frac{6}{a} \pm \frac{12}{a}) \cdot \frac{a^{2}}{6}$
	↓	Berechne die beiden Lösungen.

$x$	$=$	$3 a$
	↓	Berechne den y-Wert zu diesem x-Wert, indem du $x = 3 a$ in $f_{a}$ einsetzt.
$f_{a} (3 a)$	$=$	$\frac{1}{a^{2}} \cdot {(3 a)}^{3} - \frac{3}{a} \cdot {(3 a)}^{2} - 9 \cdot 3 a + 5 (a + 1)$
	↓	Multipliziere aus.
	$=$	$27 a - 27 a - 27 a + 5 a + 5$
	↓	Fasse die Terme mit a zusammen.
	$=$	$- 22 a + 5$
	↓	Gib das Maximum explizit an.

$x$	$=$	$3 a$	$: 3$
$a$	$=$	$\frac{x}{3}$
$y$	$=$	$- 22 \cdot a + 5$
	↓	Setze $\frac{x}{3}$ für $a$ ein.
	$=$	$- 22 \cdot \frac{x}{3} + 5$
	↓	Vereinfache den Term.
	$=$	$- \frac{22}{3} x + 5$

$f_{k}^{'} (x)$	$=$	$\frac{x^{2} \cdot k - (kx - 2) \cdot 2 x}{x^{4}}$
	↓	Kürze ein x und fasse dann Terme im Zähler zusammen.
	$=$	$\frac{xk - 2 (kx - 2)}{x^{3}}$
	$=$	$\frac{4 - kx}{x^{3}}$

$f_{k}^{''} (x)$	$=$	$\frac{x^{3} \cdot (- k) - (4 - kx) \cdot 3 x^{2}}{x^{6}}$
	↓	Kürze $x^{2}$ , multipliziere aus und fasse Terme zusammen.
	$=$	$\frac{2 kx - 12}{x^{4}}$

$0$	$=$	$A_{1}^{'} (a)$
$0$	$=$	$- \frac{4}{3} a + \frac{16}{3}$	$+ \frac{4}{3} a$
$\frac{4}{3} a$	$=$	$\frac{16}{3}$	$: \frac{4}{3}$
$a$	$=$	$4$

$A_{1} (4)$	$=$	$- \frac{2}{3} \cdot 4^{2} + \frac{16}{3} \cdot 4$
	$=$	$- \frac{2}{3} \cdot 16 + \frac{16}{3} \cdot 4$
	$=$	$- \frac{32}{3} + \frac{64}{3}$
	$=$	$\frac{32}{3}$
	$=$	$10, 6$

$2 k x - 12$	$=$	$0$	$+ 12$
$2 k x$	$=$	$12$	$: 2$
$k x$	$=$	$6$

$\lim_{x \to \sqrt{- a} \pm 0} f_{a} (x)$	$=$	$\lim_{x \to \sqrt{- a} \pm 0} \frac{- 2 (x + 5) (x - 5)}{(x + \sqrt{- a}) (x - \sqrt{- a})}$
	↓	Setze die Grenze ein.
	$=$	$\frac{- 2 (\sqrt{- a} + 5) (\sqrt{- a} - 5)}{(\sqrt{- a} + \sqrt{- a}) \underset{_{- 0 \Rightarrow 0}}{\underset{⏟}{(\sqrt{- a} - \sqrt{- a})}}}$

$0$	$=$	$F_{4} (x) .$
$0$	$=$	$- \frac{1}{3} x^{3} + 2 x^{2} - \frac{32}{3}$	$\cdot (- 3)$
$0$	$=$	$x^{3} - 6 x^{2} + 32$

$0$	$=$	$x^{2} - 8 x + 16$
	↓	Es handelt sich um eine zweite binomische Formel.
$0$	$=$	${(x - 4)}^{2}$	$\sqrt{}$
$0$	$=$		$+ 4$
$0$	$=$	$x - 4$
$4$	$=$	$x$
$x_{2,3}$	$=$	$4$

$F_{4}^{'} {(x)}_{}$	$=$	$0$
	↓	Setze $F_{4}^{'} (x) = - x^{2} + 4 x$ ein.
$- x^{2} + 4 x$	$=$	$0$
	↓	Klammere $- x$ aus.
$- x (x - 4)$	$=$	$0$

$0$	$=$	$F_{4}^{''} (x)$
$0$	$=$	$- 2 x + 4$	$+ 2 x$
$2 x$	$=$	$4$	$: 2$
$x$	$=$	$2$

$f_{a} (x)$	$=$	$\frac{- 2 x^{2} + 50}{x^{2} + a}$
	↓	Faktorisiere die Funktion für $a \leq 0$
	$=$	$\frac{- 2 (x + 5) (x - 5)}{(x + \sqrt{- a}) (x - \sqrt{- a})}$

$0$	$=$	$1 - a \cdot e^{- x}$	$+ a \cdot e^{- x}$
$a \cdot e^{- x}$	$=$	$1$	$: a$
$e^{- x}$	$=$	$\frac{1}{a}$	$\ln$
	↓	Löse nach $x$ auf.
$\ln (e^{- x})$	$=$	$\ln (\frac{1}{a})$
$- x$	$=$	$\ln (\frac{1}{a})$	$\cdot (- 1)$
$x$	$=$	$- \ln (\frac{1}{a})$
	↓	Wende ein Logarithmusgesetz an.
$x$	$=$	$- (\ln (1) - \ln (a))$
	↓	$ \ln (1) = 0$ .
$x$	$=$	$\ln (a)$

Aufgaben zur Diskussion von Funktionenscharen

Graphische Darstellung

2 Gerade bestimmen, auf der alle Maxima liegen

Krümmungsverhalten zusammenfassend

Überprüfung der Lösung für k=3

Nullstellen berechnen

Integral aufstellen

Alternativer Rechenweg für die Nullstelle

Extrema bestimmen

Extremum für x=0

Extremum für x=4

Wendepunkt bestimmen

Nullstellen bestimmen

Y-Achsenabschnitt bestimmen

Skizze:

Fallunterscheidung

Fallunterscheidung

limx→−∞⁡(x⋅eax+3a)=limx→−∞⁡x⋅eax⏟→0+3a=3a

Tabelle für f−3(x)=x⋅e−3x−1:

Tabelle für f1=x⋅ex+3:

Die Graphen von K−3 und von K1.

Fallunterscheidung

Tabelle für f−1(x)=x−e−x−1

Tabelle für f1=x+e−x+1

Graphen von K−1 und von K1.

Extremum für $x = 0$

Extremum für $x = 4$

$\lim_{x \to - \infty} (x \cdot e^{a x} + \frac{3}{a}) = \lim_{x \to - \infty} \underset{\to 0}{\underset{⏟}{x \cdot e^{a x}}} + \frac{3}{a} = \frac{3}{a}$

Tabelle für $f_{- 3} (x) = x \cdot e^{- 3 x} - 1$ :

Tabelle für $f_{1} = x \cdot e^{x} + 3$ :

Die Graphen von $K_{- 3}$ und von $K_{1}$ .

Tabelle für $f_{- 1} (x) = x - e^{- x} - 1$

Tabelle für $f_{1} = x + e^{- x} + 1$

Graphen von $K_{- 1}$ und von $K_{1}$ .