Aufgaben zur Diskussion von Funktionenscharen

$f_{a} (x) = - \frac{4}{a^{2}} (8 - a) (x^{2} - ax)$ mit $a \in ℝ \ {0; 8}$

Bestimme den Flächeninhalt $A (a)$ der Fläche zwischen $G_{f_{a}}$ und der x-Achse.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion finden

Nullstellen berechnen

Bestimme zuerst die Nullstellen der Funktion. Setze also die Funktion gleich 0.

$f_{a} (x)$	$=$	$0$
	↓	Setze $f_{a} (x) = - \frac{4}{a^{2}} (8 - a) (x^{2} - ax)$ ein.
$- \frac{4}{a^{2}} (8 - a) (x^{2} - ax)$	$=$	$0$	$: (- \frac{4}{a^{2}} (8 - a))$
	↓	Es wird durch alles, dass kein $x$ enthält dividiert , da dies keine Auswirkung auf die Nullstellen hat.
$x^{2} - a x$	$=$	$0$
	↓	$x$ wird ausgeklammert.
$x (x - a)$	$=$	$0$

Diese Gleichung ist dann Null, wenn entweder die Zahl vor der Klammer oder das Innere der Klammer gleich 0 ist.

$x_{1} = 0, x_{2} = a$

Integral aufstellen

Jetzt kannst du ein Integral aufstellen, um die vom Graphen $G_{f a}$ und der $x$ -Achse eingeschlossene Fläche $A (a)$ zu berechnen. Die Fläche befindet sich zwischen den beiden Nullstellen von $f_{a}$ .

$A (a)$	$=$	$\| \int_{0}^{a} - \frac{4}{a^{2}} (8 - a) (x^{2} - a x) dx \|$
	↓	Der Term $- \frac{4}{a^{2}} (8 - a)$ wird vor das Integral gezogen. Er hängt nicht von $x$ ab.
	$=$	$\| - \frac{4}{a^{2}} (8 - a) \int_{0}^{a} (x^{2} - a x) dx \|$
	↓	Bestimme eine Stammfunktion von $(x^{2} - a x)$ , um das Integral zu berechnen.
	$=$	$\| - \frac{4}{a^{2}} (8 - a) {[\frac{1}{3} x^{3} - a \frac{1}{2} x^{2}]}_{0}^{a} \|$
	↓	In die Klammer wird für $x$ die obere Grenze $(a)$ eingesetzt und minus die Klammer mit der unteren Grenze $(0)$ gerechnet.
	$=$	$\| - \frac{4}{a^{2}} (8 - a) [(\frac{1}{3} a^{3} - a \frac{1}{2} a^{2}) - (\frac{1}{3} 0^{3} - a \frac{1}{2} 0^{2})] \|$
	$=$	$\| - \frac{4}{a^{2}} (8 - a) (\frac{1}{3} a^{3} - \frac{1}{2} a^{3}) \|$
	$=$	$\| - \frac{4}{a^{2}} (8 - a) (- \frac{1}{6} a^{3}) \|$
	$=$	$\| \frac{4}{6 a^{2}} (8 a^{3} - a^{4}) \|$
	$=$	$\| \frac{2}{3} (8 a - a^{2}) \|$
	$=$	$\| \frac{2}{3} (8 a - a^{2}) \|$
	↓	Multipliziere nun die Klammer aus und sortiere nach Potenzen.
	$=$	$\| - \frac{2}{3} a^{2} + \frac{16}{3} a \|$

Um die Betragsstriche weglassen zu können und später leichter rechnen zu können, kannst du dir überlegen, wann das Innere $- \frac{2}{3} a^{2} + \frac{16}{3} a$ positiv ist und wann negativ.

$- \frac{2}{3} a^{2} + \frac{16}{3} a = - \frac{2}{3} (a^{2} - 8 a) = - \frac{2}{3} \cdot a \cdot (a - 8)$

Der Term $- \frac{2}{3} \cdot a \cdot (a - 8)$ wäre Null für $a = 0$ und $a = 8$ . Somit schaust du dir die folgenden Bereiche an:

$a < 0$
$0 < a < 8$ und
$a > 8$

In einer Vorzeichentabelle siehst du, wann $- \frac{2}{3} \cdot a \cdot (a - 8)$ positiv ist und wann negativ:

	$a < 0$	$0 < a < 8$	$a > 8$
$- \frac{2}{3}$	$-$	$-$	$-$
$a$	$-$	$+$	$+$
$a - 8$	$-$	$-$	$+$

$- \frac{2}{3} \cdot a \cdot (8 - a)$	$-$	$+$	$-$

$\Rightarrow - \frac{2}{3} a^{2} + \frac{16}{3} > 0$ für $0 < a < 8$ und sonst ist $- \frac{2}{3} a^{2} + \frac{16}{3} < 0$

Antwort: $A (a) = {\begin{matrix} - \frac{2}{3} a^{2} + \frac{16}{3} a & 0 < a < 8 \\ \frac{2}{3} a^{2} - \frac{16}{3} a & sonst \end{matrix}$

Für welche $a$ ist der Inhalt der Fläche $A (a)$ gleich 8?

Bestimme für $0 < a < 8$ den Flächeninhalt $A (a)$ so, dass dieser möglichst groß wird. Gib den maximalen Flächeninhalt an.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Maximum
Der Maximalwert der Fläche ist das gleiche, wie das Maximum der Funktion .
Um dieses zu bestimmen, muss $A_{1} (a)$ ( $A_{1} = - \frac{2}{3} a^{2} + \frac{16}{3} a$ ) abgeleitet werden.
$A_{1}^{'} (a) = - \frac{4}{3} a + \frac{16}{3}$
Der Graph von $A_{1} (a)$ ist eine nach unten geöffnete Parabel, d.h. es gibt nur ein Maximum. Das gesuchte Maximum ist die Nullstelle der Ableitung, demnach wird $\frac{dA}{da}$ gleich $0$ gesetzt.
$0$ $=$ $A_{1}^{'} (a)$
$0$ $=$ $- \frac{4}{3} a + \frac{16}{3}$ $+ \frac{4}{3} a$
$\frac{4}{3} a$ $=$ $\frac{16}{3}$ $: \frac{4}{3}$
$a$ $=$ $4$
Die Bedingung in der Aufgabenstellung $0 < a < 8$ ist für $a = 4$ erfüllt.
Die Stelle, an der $A_{1} (a)$ den größten Wert hat ist bekannt, wie hoch dieser ist wird ermittelt, indem das berechnete $a$ in $A_{1} (a)$ eingesetzt wird.
$A_{1} (4)$ $=$ $- \frac{2}{3} \cdot 4^{2} + \frac{16}{3} \cdot 4$
$=$ $- \frac{2}{3} \cdot 16 + \frac{16}{3} \cdot 4$
$=$ $- \frac{32}{3} + \frac{64}{3}$
$=$ $\frac{32}{3}$
$=$ $10, 6$
Antwort: Der maximale Flächeninhalt beträgt $\frac{32}{3}$ FE.

$F_{4} (x) = \int_{4}^{x} f_{4} (t) dt$ Bestimme den Term $F_{4} (x)$ und alle Nullstellen von $F_{4}$

Berechne die Hoch-, Tief- und Wendepunkte von $G_{F_{4}}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema
Leite $F_{4} (x) = - \frac{1}{3} x^{3} + 2 x^{2} - \frac{32}{3}$ zweimal ab.
$F_{4}^{'} (x) = - x^{2} + 4 x$
$F_{4}^{''} (x) = - 2 x + 4$
Extrema bestimmen
Bestimme die Extrema von $F_{4} (x)$ .
$F_{4}^{'} {(x)}_{}$ $=$ $0$
↓
Setze $F_{4}^{'} (x) = - x^{2} + 4 x$ ein.
$- x^{2} + 4 x$ $=$ $0$
↓
Klammere $- x$ aus.
$- x (x - 4)$ $=$ $0$
Die Gleichung ist gleich 0, wenn ein Element der Multiplikation ( $- x \cdot (x - 4)$ ) Null ist.
$- x = 0$ für $x = 0$
$x - 4 = 0$ für $x = 4$
$x_{1} = 0, x_{2} = 4$
Extremum für $x = 0$
Setze die gefundene Nullstelle $x = 0$ der Ableitung von $F_{4} (x)$ in $F_{4} (x)$ ein.
$F_{4} (x) = - \frac{1}{3} x^{3} + 2 x^{2} - \frac{32}{3}$
$F_{4} (0) = - \frac{1}{3} \cdot 0^{3} + 2 \cdot 0^{2} - \frac{32}{3} = - \frac{32}{3}$
Setze jetzt $x = 0$ in $F_{4}^{''} (x) = - 2 x + 4$ ein.
$F_{4}^{''} (0) = - 2 \cdot 0 + 4 = 4$
Da $F_{4}^{''} (0) > 0$ ist, hat $F_{4} (x)$ an der Stelle $x_{1} = 0$ einen Tiefpunkt $TP (0 | - \frac{32}{3})$ .
Extremum für $x = 4$
Setze die gefundene Nullstelle $x = 4$ der Ableitung von $F_{4} (x)$ in $F_{4} (x)$ ein.
$F_{4} (x) = - \frac{1}{3} x^{3} + 2 x^{2} - \frac{32}{3}$
$F_{4} (4) = - \frac{1}{3} \cdot 4^{3} + 2 \cdot 4^{2} - \frac{32}{3} = 0$
Setze jetzt $x = 4$ in $F_{4}^{''} (x) = - 2 x + 4$ ein.
$F_{4}^{''} (4) = - 2 \cdot 4 + 4 = - 4$
Da $F_{4}^{''} (4) < 0$ ist, hat $F_{4} (x)$ an der Stelle $x_{2} = 4$ einen Hochpunkt $HP (4 | 0)$
Wendepunkt bestimmen
Bestimme nun den Wendepunkt.
Setze dafür die zweite Ableitung $F_{4}^{''} (x) = - 2 x + 4$ gleich $0$ .
$0$ $=$ $F_{4}^{''} (x)$
$0$ $=$ $- 2 x + 4$ $+ 2 x$
$2 x$ $=$ $4$ $: 2$
$x$ $=$ $2$
Setze $x = 2$ in $F_{4} (x)$ ein.
$F_{4} (2) = - \frac{1}{3} \cdot 2^{3} + 2 \cdot 2^{2} - \frac{32}{3} = - \frac{16}{3}$
Damit ergeben sich die Koordinaten des Wendepunktes $W P (2 | - \frac{16}{3})$ .
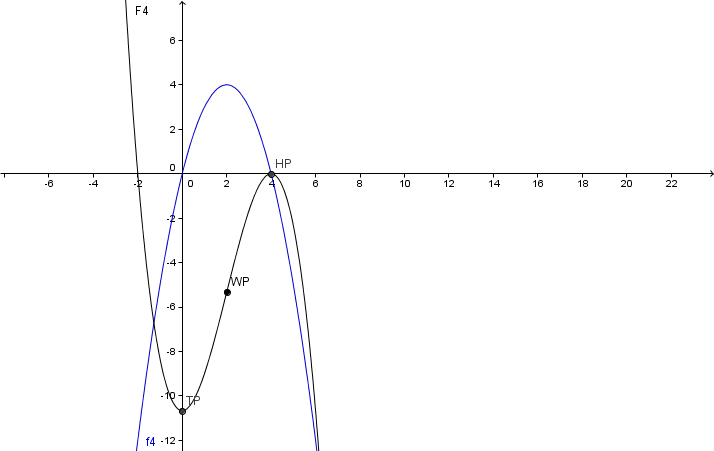
Skizziere $G_{f_{4}}$ und $G_{F_{4}}$ im selben Koordinatensystem.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$8$	$=$	$A (a)$
	↓	Setze $A_{1} = - \frac{2}{3} a^{2} + \frac{16}{3} a$ ein.
$8$	$=$	$- \frac{2}{3} a^{2} + \frac{16}{3} a$	$- 8$
$0$	$=$	$- \frac{2}{3} a^{2} + \frac{16}{3} a - 8$
	↓	Wende die Mitternachtsformel an.
$a_{1,2}$	$=$	$\frac{- \frac{16}{3} \pm \sqrt{{(\frac{16}{3})}^{2} - 4 (- \frac{2}{3}) (- 8)}}{2 (- \frac{2}{3})}$
	↓	Multipliziere unter der Wurzel aus.
$a_{1,2}$	$=$	$\frac{- \frac{16}{3} \pm \sqrt{\frac{256}{9} - \frac{64}{3}}}{2 (- \frac{2}{3})}$
	↓	Fasse zusammen.
$a_{1,2}$	$=$	$\frac{- \frac{16}{3} \pm \sqrt{\frac{64}{9}}}{- \frac{4}{3}}$
$a_{1,2}$	$=$	$\frac{- \frac{16}{3} \pm \frac{8}{3}}{- \frac{4}{3}}$
$a_{1,2}$	$=$	$- \frac{3}{4} (- \frac{16}{3} \pm \frac{8}{3})$
$a_{1,2}$	$=$	$4 \mp 2$

$8$	$=$	$A (a)$
	↓	Setze $A_{2} = \frac{2}{3} a^{2} - \frac{16}{3} a$ ein.
$8$	$=$	$\frac{2}{3} a^{2} - \frac{16}{3} a$	$- 8$
$0$	$=$	$\frac{2}{3} a^{2} - \frac{16}{3} a - 8$
	↓	Wende die Mitternachtsformel an.
$a_{3,4}$	$=$	$\frac{\frac{16}{3} \pm \sqrt{{(\frac{16}{3})}^{2} - 4 (\frac{2}{3}) (- 8)}}{2 (\frac{2}{3})}$
	↓	Multipliziere unter der Wurzel aus.
$a_{3,4}$	$=$	$\frac{\frac{16}{3} \pm \sqrt{\frac{256}{9} + \frac{64}{3}}}{2 (\frac{2}{3})}$
	↓	Fasse zusammen.
$a_{3,4}$	$=$	$\frac{\frac{16}{3} \pm \sqrt{\frac{448}{9}}}{\frac{4}{3}}$
$a_{3,4}$	$=$	$\frac{3}{4} (\frac{16}{3} \pm \frac{8 \sqrt{7}}{3})$
$a_{3,4}$	$=$	$4 \pm 2 \sqrt{7}$

$f_{4} (t)$	$=$	$\int_{4}^{x} f_{4} (t) dt$
	$=$	$\int_{4}^{x} (- t^{2} + 4 t) dt$
	↓	Integriere.
	$=$	${[- \frac{1}{3} t^{3} + \frac{4}{2} t^{2}]}_{4}^{x}$
	↓	In die Klammer wird für $t$ die obere Grenze $(x)$ eingesetzt und minus die Klammer mit der unteren Grenze $(4)$ gerechnet.
	$=$	$[- \frac{1}{3} x^{3} + \frac{4}{2} x^{2}] - [- \frac{1}{3} 4^{3} + \frac{4}{2} 4^{2}]$
	$=$	$- \frac{1}{3} x^{3} + \frac{4}{2} x^{2} + \frac{64}{3} - 32$
	$=$	$- \frac{1}{3} x^{3} + 2 x^{2} - \frac{32}{3}$

$0$	$=$	$x^{2} - 8 x + 16$
$x_{2,3}$	$=$	$\frac{8 \pm \sqrt{{(8)}^{2} - 4 \cdot (1) \cdot (16)}}{2 \cdot (1)}$
$x_{2,3}$	$=$	$\frac{8 \pm \sqrt{(64 - 64)}}{2}$
$x_{2,3}$	$=$	$\frac{8}{2}$
$x_{2,3}$	$=$	$4$

$0$	$=$	$A_{1}^{'} (a)$
$0$	$=$	$- \frac{4}{3} a + \frac{16}{3}$	$+ \frac{4}{3} a$
$\frac{4}{3} a$	$=$	$\frac{16}{3}$	$: \frac{4}{3}$
$a$	$=$	$4$

$A_{1} (4)$	$=$	$- \frac{2}{3} \cdot 4^{2} + \frac{16}{3} \cdot 4$
	$=$	$- \frac{2}{3} \cdot 16 + \frac{16}{3} \cdot 4$
	$=$	$- \frac{32}{3} + \frac{64}{3}$
	$=$	$\frac{32}{3}$
	$=$	$10, 6$

$0$	$=$	$F_{4} (x) .$
$0$	$=$	$- \frac{1}{3} x^{3} + 2 x^{2} - \frac{32}{3}$	$\cdot (- 3)$
$0$	$=$	$x^{3} - 6 x^{2} + 32$

$0$	$=$	$x^{2} - 8 x + 16$
	↓	Es handelt sich um eine zweite binomische Formel.
$0$	$=$	${(x - 4)}^{2}$	$\sqrt{}$
$0$	$=$		$+ 4$
$0$	$=$	$x - 4$
$4$	$=$	$x$
$x_{2,3}$	$=$	$4$

$F_{4}^{'} {(x)}_{}$	$=$	$0$
	↓	Setze $F_{4}^{'} (x) = - x^{2} + 4 x$ ein.
$- x^{2} + 4 x$	$=$	$0$
	↓	Klammere $- x$ aus.
$- x (x - 4)$	$=$	$0$

$0$	$=$	$F_{4}^{''} (x)$
$0$	$=$	$- 2 x + 4$	$+ 2 x$
$2 x$	$=$	$4$	$: 2$
$x$	$=$	$2$

Aufgaben zur Diskussion von Funktionenscharen

Nullstellen berechnen

Integral aufstellen

Alternativer Rechenweg für die Nullstelle

Extrema bestimmen

Extremum für x=0

Extremum für x=4

Wendepunkt bestimmen

Extremum für $x = 0$

Extremum für $x = 4$