Pflichtteil
- 1
Ableitung
Bilden Sie die Ableitung der Funktion mit
Bilden Sie die Ableitung der Funktion mit
Bilden Sie die Ableitung der Funktion mit
Bilden Sie die Ableitung der Funktion mit .
Bilden Sie die Ableitung der Funktion mit .
Bilden Sie die erste Ableitung der Funktion mit und vereinfachen Sie so weit wie möglich.
- 2
Stammfunktion und Integral
Gegeben ist die Funktion mit .
Bestimmen Sie eine Stammfunktion von .
Gegeben ist die Funktion mit . Bestimmen Sie diejenige Stammfunktion von , deren Schaubild den Punkt enthält.
Zeigen Sie, dass eine Stammfunktion von ist.
Berechnen Sie das Integral .
Berechnen Sie das Integral .
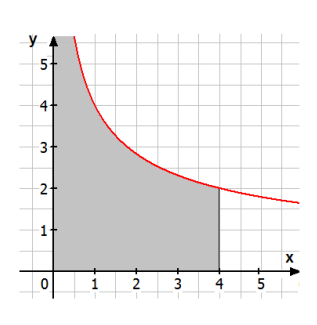
Die Funktion f mit schließt mit der x-Achse, der Geraden und der y-Achse eine nach oben offene Fläche ein (siehe Skizze). Untersuchen Sie, ob diese Fläche einen endlichen Flächeninhalt hat und bestimmen Sie diesen gegebenenfalls.
- 3
Gleichungslehre
Lösen Sie die Gleichung
Lösen Sie die Gleichung
Lösen Sie die Gleichung
Lösen Sie die Gleichung
Lösen Sie für die Gleichung
Lösen Sie die Gleichung
Lösen Sie die Gleichung
Lösen Sie für die Gleichung
- 4
Elemente der Kurvendiskussion
Bestimmen Sie die Extrempunkte der Funktion mit
Bestimmen Sie den Wendepunkt der Funktion mit
Gegeben ist die Funktion mit
a) Bestimmen Sie die Gleichung der Normalen von im Punkt .
b) Bestimmen Sie den Schnittpunkt der Normalen mit der x-Achse.
Die Funktion hat das nebenstehende Schaubild und die Funktionsgleichung
,
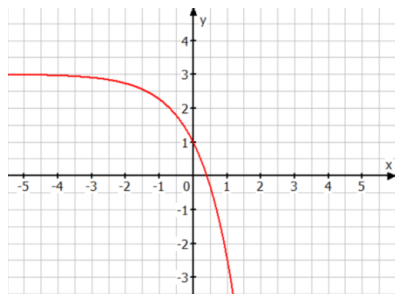
a) Bestimmen Sie die Werte von und .
b) Berechnen Sie, an welcher Stelle die Funktion die Steigung besitzt.
Gegeben sind die Funktionen und mit und .
Geben Sie die waagrechte Asymptote der Funktion an.
Bestimmen Sie die Stelle, an der und die gleiche Steigung haben.
Gegeben ist die Funktion mit
a) Skizzieren Sie das Schaubild von .
b) Berechnen Sie die Gleichung der Tangente an den Graphen von an der Stelle und zeichnen Sie die Tangente ein.
Gegeben ist die Funktion mit .
a) Berechnen Sie die Steigung von an der Stelle .
b) Berechnen Sie die Stelle, an der die Funktion die Steigung hat.
c) Bestimmen Sie die Gleichung der Tangente an der Stelle .
Gegeben ist die Funktion mit
a) Skizzieren Sie das Schaubild von für .
b) Bestimmen Sie die Steigung von an der Stelle .
c) Bestimmen Sie so, dass der Ursprung auf dem Schaubild von liegt.
- 5
Funktionskompetenz
Die Abbildung zeigt das Schaubild der Ableitung einer Funktion . Begründen Sie, ob folgende Aussagen über die Funktion wahr, falsch oder unentscheidbar sind.
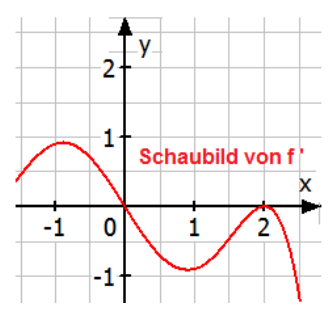
a) An der Stelle hat das Schaubild von einen Hochpunkt.
b) Für ist .
c) Das Schaubild von ist punktsymmetrisch zum Ursprung für .
d) An der Stelle hat das Schaubild von einen Wendepunkt.
Die Abbildung zeigt das Schaubild der Ableitung einer Funktion .
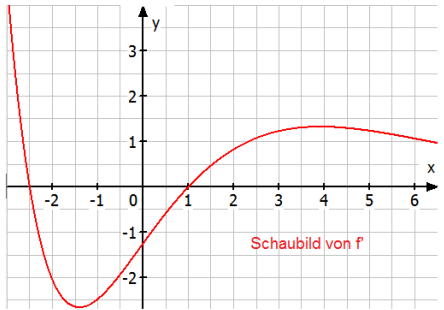
a) Begründen Sie, welche Aussagen man in dem dargestellten Bereich hinsichtlich der Anzahl der
- Extremstellen,
- Wendestellen
und Nullstellen
von man treffen kann.
b) Begründen Sie, dass gilt.
Die Abbildung zeigt das Schaubild der Ableitung einer Funktion .
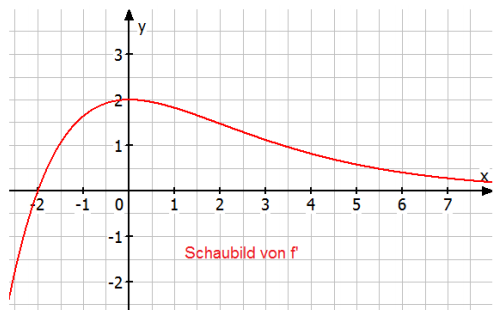
Begründen Sie, ob folgende Aussagen über die Funktion wahr, falsch oder unentscheidbar sind.
a) Bei besitzt das Schaubild von einen Extrempunkt.
b) Bei besitzt das Schaubild von f eine waagrechte Tangente.
c) Das Schaubild der Funktion besitzt keine Wendepunkte.
d) für .
Gegeben sind die Schaubilder zweier Funktionen und Eine der beiden Funktionen ist die Ableitungsfunktion der anderen Funktion.
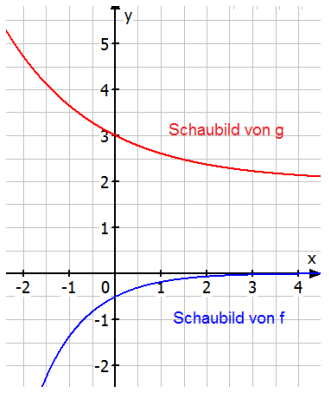
a) Begründen Sie, dass die Funktion die Ableitung der Funktion ist.
b) Die Funktion hat die Funktionsgleichung . Bestimmen Sie und
Die 4 Abbildungen zeigen die Schaubilder von Funktionen. Eines dieser Schaubilder gehört zu der Funktion mit .
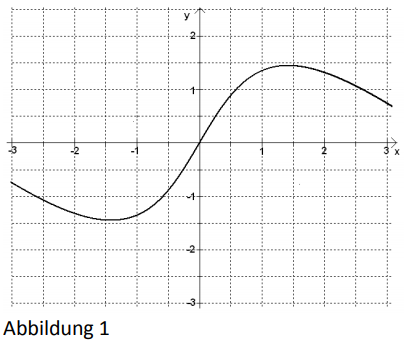
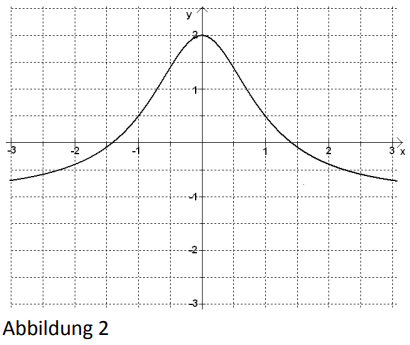
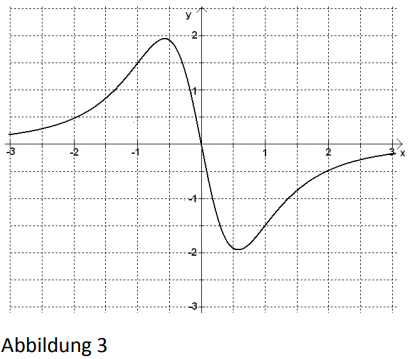
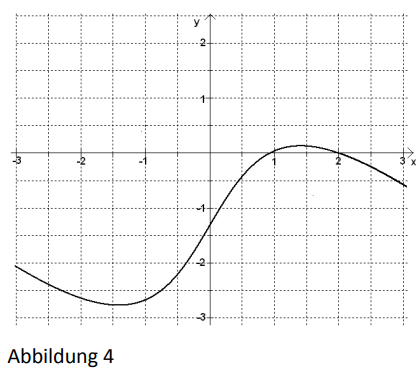
a) Begründen Sie, dass Abbildung 2 zur Funktion gehört. Bestimmen Sie den Wert von a.
b) Von den anderen drei Abbildungen gehört eine zur Ableitungsfunktion und eine zur Integralfunktion mit . Ordnen Sie diesen beiden Funktionen die zugehörigen Abbildungen zu und begründen Sie jeweils Ihre Zuordnung.
- 6
Lineare Gleichungssysteme, Inzidenzgeometrie
Bestimmen Sie die Lösungsmenge des Linearen Gleichungssystems.
Stellen Sie den Vektor als Linearkombination der drei Vektoren
, und dar.
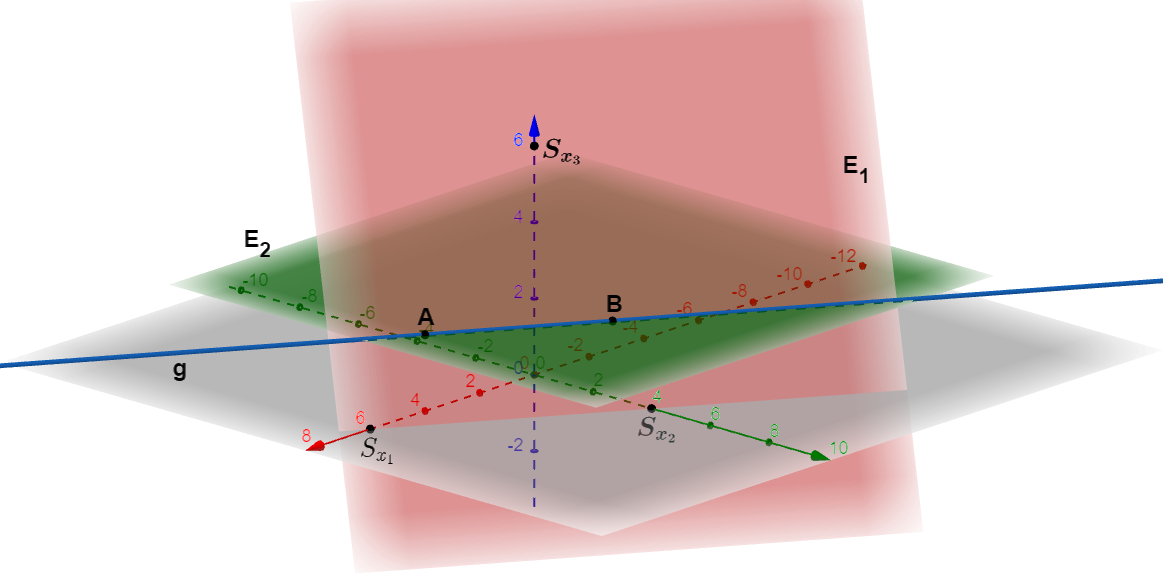
Gegeben sind die Ebenen und
a) Stellen Sie die Ebenen und in einem gemeinsamen Koordinatensystem dar.
b) Zeichnen Sie die Schnittgerade von und ein und bestimmen Sie die Gleichung der Schnittgeraden.
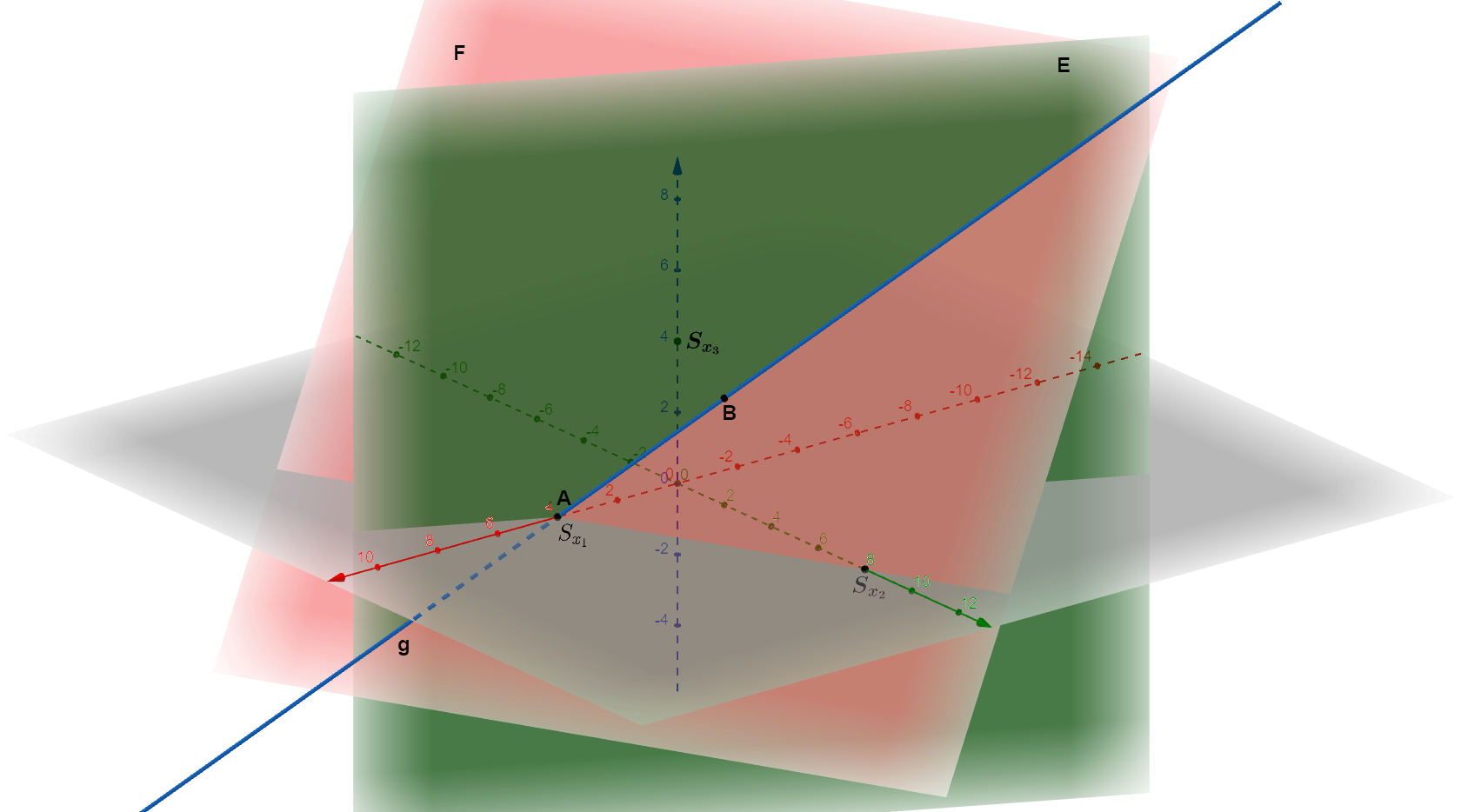
Gegeben sind die Ebenen und
a) Stellen Sie die Ebenen und in einem gemeinsamen Koordinatensystem dar.
b) Zeichnen Sie die Schnittgerade von und ein und bestimmen Sie die Gleichung der Schnittgeraden.
a) Geben Sie die Gleichung der Ebene an, welche die Spurpunkte und und keinen Schnittpunkt mit der -Achse hat.
b) Geben Sie die Gleichung der Ebene an, welche den Punkt ) enthält und parallel zur Ebene ist.
c) Geben Sie die Gleichung der Geraden an, welche durch den Punkt geht und senkrecht zur Ebene
steht.
Gegeben sind die Geraden und mit und
a) Zeigen Sie, dass und parallel, aber nicht identisch sind.
b) Geben Sie eine Gleichung der Ebene an, in der die Geraden und liegen.
- 7
Metrische Geometrie
Gegeben sind die beiden Ebenen und mit
; und
a) Weisen Sie nach, dass und parallel zueinander liegen.
b) Bestimmen Sie den Abstand von und .
Gegeben sind die Punkte und Die Ebene enthält die Punkte und
a) Bestimmen Sie die Gleichung von in Normalenform und Koordinatenform.
b) Untersuchen Sie die Lage der Ebene zur Geraden mit
Gegeben ist die Gerade mit ; und mit
;
a) Zeigen Sie, dass die Geraden und orthogonal zueinander liegen.
b) Untersuchen Sie, ob sich und auch schneiden.
Gegeben sind die Punkte , und
a) Zeigen Sie, dass das Dreieck rechtwinklig ist.
b) Berechnen Sie den Flächeninhalt des Dreiecks .
Gegeben sind die Punkte und .
Berechnen Sie den Flächeninhalt des Dreiecks .
Gegeben sind die Punkte und .
a) Zeigen Sie, dass das Dreieck gleichschenklig ist.
b) Das Dreieck lässt sich so durch einen Punkt ergänzen, dass eine Raute entsteht. Bestimmen Sie die Koordinaten von .
c) Berechnen Sie den Flächeninhalt des Dreiecks .
- 8
Stochastik
Ein Auto hat einen Wert von 30000€ und soll von eine Versicherung jährlich gegen Schäden versichert werden.
Die Autoversicherung erwartet, dass bei 10000 versicherten Autos des gleichen Typs pro Jahr folgende Schadensfälle passieren:
- 10 Versicherungsfälle mit einem Totalschaden,
- 50 Versicherungsfälle mit einem durchschnittlichen Schaden von 10000€,
- 250 kleinere Schäden mit einem durchschnittlichen Schaden von 2000€.
Berechnen Sie, welchen Versicherungsbeitrag die Versicherung jährlich anbieten sollte, wenn Sie pro Kunden einen Gewinn von 100 € (ohne Verwaltungskosten) erwirtschaften möchte.
Ein Biathlet trifft erfahrungsgemäß bei 80% seiner Schüsse die Scheibe.
a) Berechnen Sie, mit welcher Wahrscheinlichkeit er bei drei Schüssen
- nur den mit dem ersten Schuss
- mindestens einen Schuss trifft.
b) Für ein Ereignis gilt: . Geben Sie geeignete Werte für , und an. Beschreiben Sie das Ereignis in Worten.
Ein Chuck-your-luck ist ein Würfelspiel aus Amerika. Der Spieler setzt einen Dollar und würfelt dann dreimal. Für jede Sechs erhält er von der Bank einen Dollar.
a) Die Zufallsvariable soll den Gewinn des Spielers angeben. Geben Sie die möglichen Werte von und ihre jeweilige Wahrscheinlichkeit an.
b) Untersuchen Sie, ob das Spiel fair ist.
Auf einem Tisch liegen verdeckt Kreuz-Karten und Herz-Karten.Es werden zwei Karten aufgedeckt.
Berechnen Sie, für welche Werte von die Wahrscheinlichkeit, dass unter den aufgedeckten Karten genau eine Herzkarte ist, gleich ist.
In einem Behälter befinden sich weiße und schwarze Kugeln. Es werden Kugeln mit Zurücklegen gezogen.
a) Berechnen Sie die Wahrscheinlichkeit, dass mindestens eine der beiden Kugeln weiß ist.
b) Berechnen Sie, wie viele weiße Kugeln sich in dem Behälter befinden müssten, damit die Wahrscheinlichkeit, mindestens eine weiße Kugel zu ziehen, betragen hätte.
- 9
Beschreiben, Verstehen, Begründen
Gegeben sind zwei zueinander parallele Ebenen und . Die Ebene ist parallel zu und und hat von beiden Ebenen den gleichen Abstand.
Beschreiben Sie ein Verfahren, mit dem man eine Gleichung der Ebene bestimmen kann.
Gegeben ist eine Ebene . Gesucht ist eine zu parallele Ebene im
Abstand 3.
Beschreiben Sie ein Verfahren, mit dem man eine Gleichung der Ebene bestimmen kann.
Die vier Punkte und bilden ein Parallelogramm im Raum. Des Weiteren ist ein Punkt gegeben.
Beschreiben Sie ein Verfahren, um festzustellen ob der Punkt im Parallelogramm liegt.
Skizzieren Sie das Schaubild einer Funktion mit folgenden Eigenschaften:
und
Begründen Sie: Ist , so ist das Schaubild von eine Rechtskurve.
Für ein Ereignis bei der mehrmaligen Durchführung eines Bernoulli-Experimentes gilt
Beschreiben Sie das Ereignis in Worten.