Aufgaben zur Spiegelung an einer Ursprungsgeraden
Wie gut kennst du dich mit dem Spiegeln aus? Lerne mit diesen Aufgaben, Punkte und Geraden an Ursprungsgeraden zu spiegeln!
- 1
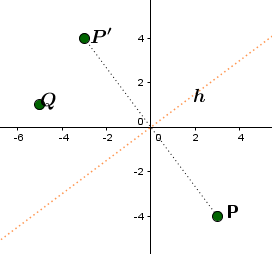
Spiegle den Punkt an der Ursprungsgeraden und gib die Koordinaten des Bildpunktes an.
Gib den Punkt jeweils in das Eingabefeld ein, zum Beispiel:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgerade
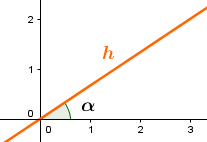
Der Punkt soll an der Geraden gespiegelt werden:
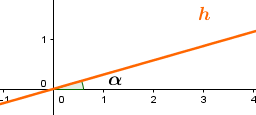
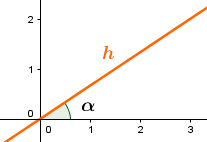
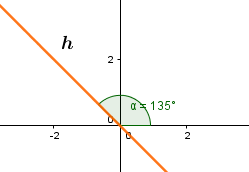
Um den Punkt an der Geraden zu spiegeln, benötigt man als erstes den Winkel , den die Gerade mit der x-Achse einschließt.
Somit ergibt sich folgende Gleichung:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgerade
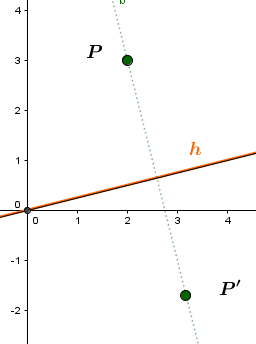
Der Punkt soll an der Geraden gespiegelt werden:
Um den Punkt an der Geraden zu spiegeln, benötigt man als erstes den Winkel , den die Gerade mit der x-Achse einschließt.
Somit ergibt sich folgende Gleichung:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgerade
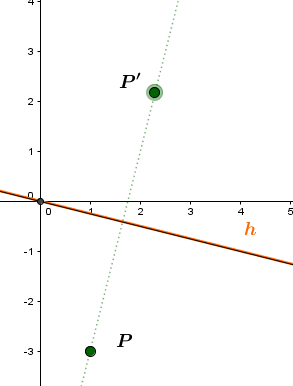
Der Punkt soll an der Geraden gespiegelt werden:
Um den Punkt an der Geraden zu spiegeln, benötigt man als erstes den Winkel , den die Gerade mit der x-Achse einschließt.
Somit ergibt sich folgende Gleichung:
- 2
Spiegle den Punkt an der Ursprungsgeraden und gib die Koordinaten des Bildpunktes an.
,
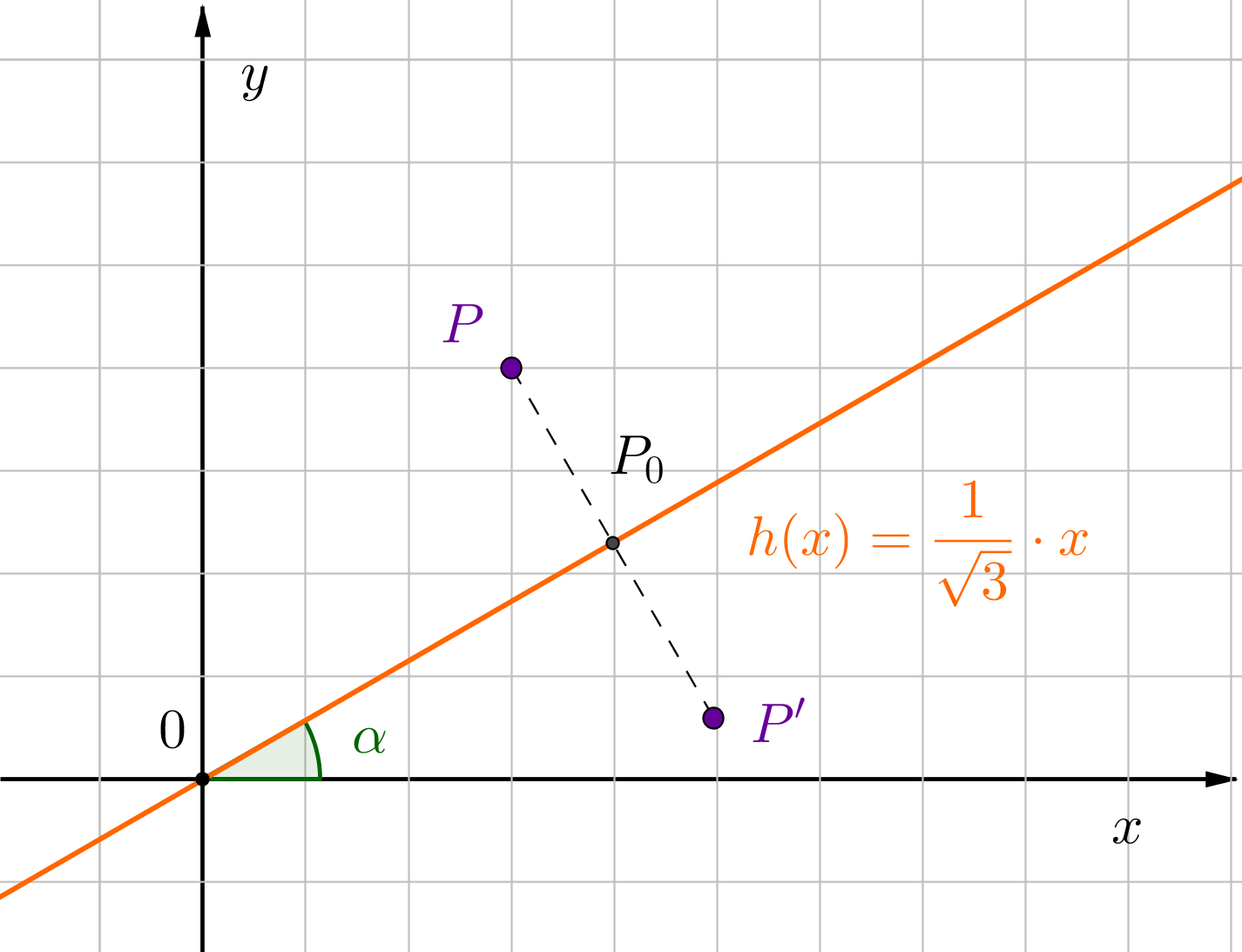
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
Die Steigung der Geraden ist . Das bedeutet, dass der Winkel ist.
Alternative 1: Lösung in Koordinatenform:
Setze den Winkel in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Winkel in die Matrix ein.
Setze die Koordinaten des Punktes in den Vektor ein.
Führe die Matrix-Vektor-Multiplikation aus.
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
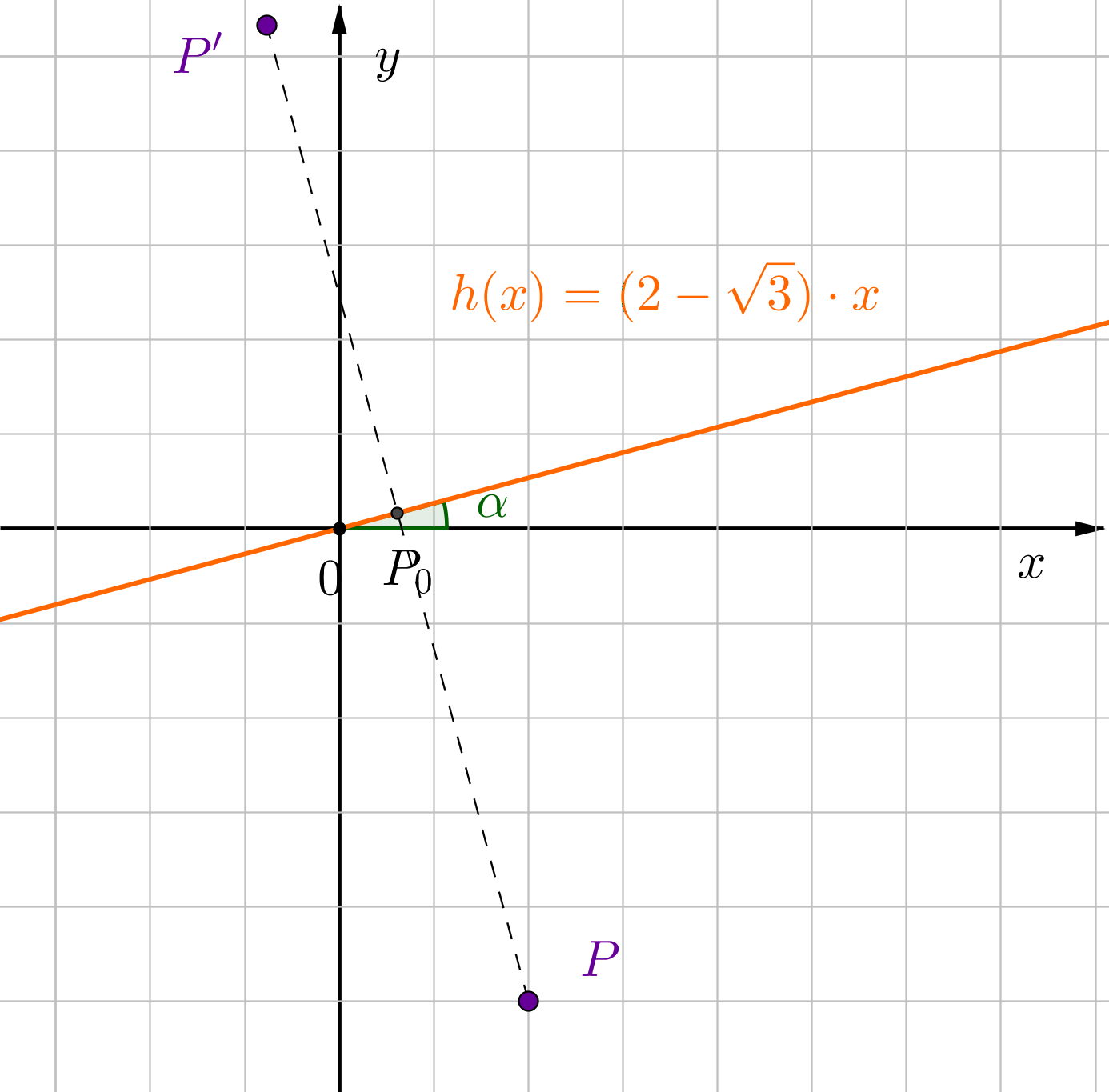
Die Steigung der Geraden ist . Das bedeutet, dass der Winkel ist.
Alternative 1: Lösung in Koordinatenform:
Setze den Winkel in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Winkel in die Matrix ein.
Setze die Koordinaten des Punktes in den Vektor ein.
Führe die Matrix-Vektor-Multiplikation aus.
,
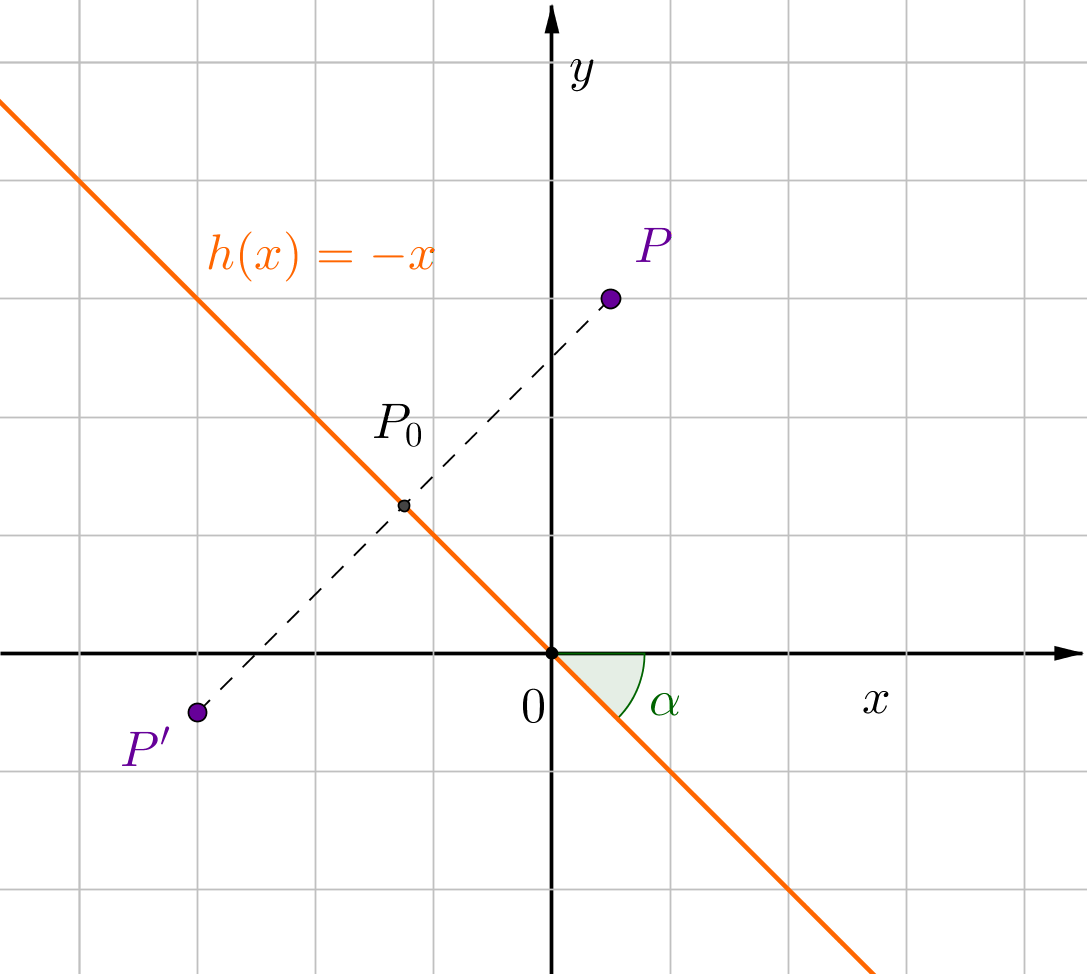
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
Die Steigung der Geraden ist . Das bedeutet, dass der Winkel ist.
Alternative 1: Lösung in Koordinatenform:
Setze den Winkel in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Winkel in die Matrix ein.
Setze die Koordinaten des Punktes in den Vektor ein.
Führe die Matrix-Vektor-Multiplikation aus.
,
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
Die Steigung der Geraden ist . Das bedeutet, dass der Winkel ist.
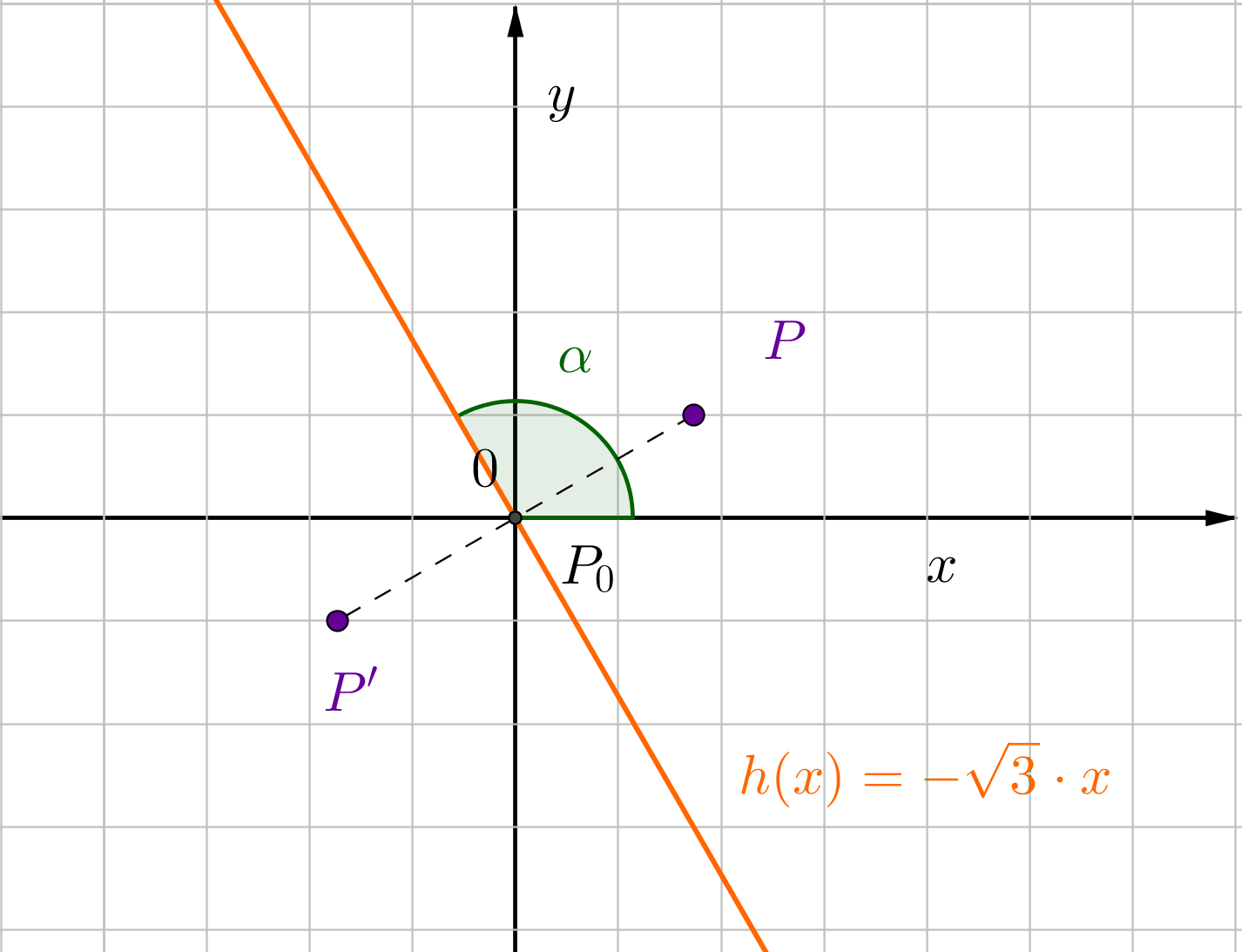
Alternative 1: Lösung in Koordinatenform:
Setze den Winkel in das Gleichungssystem ein.
Setze die Koordinaten des Punktes in das Gleichungssystem ein.
Alternative 2: Lösung in Matrixform:
Setze den Winkel in die Matrix ein.
Setze die Koordinaten des Punktes in den Vektor ein.
Führe die Matrix-Vektor-Multiplikation aus.
- 3
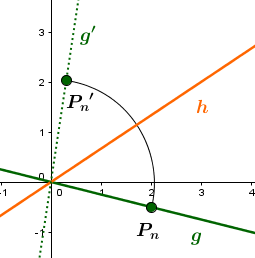
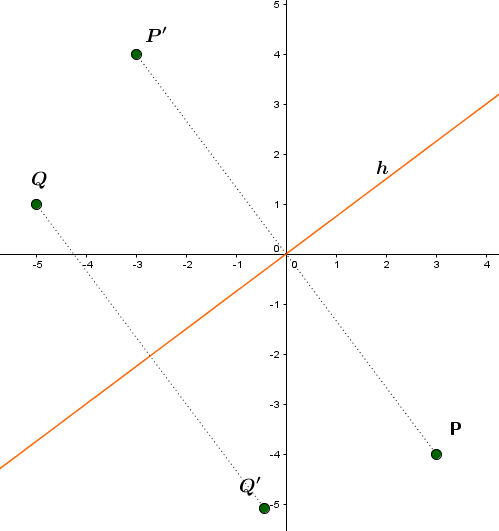
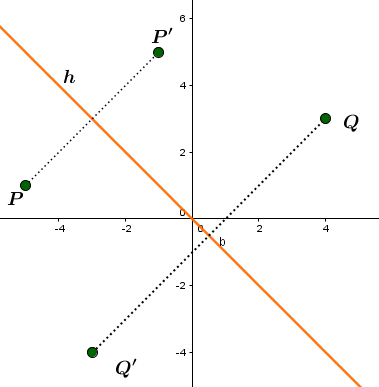
Spiegle die Gerade an der Ursprungsgeraden und gib die Gleichung der Bildgeraden an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung einer Geraden an einer Ursprungsgeraden
Somit ergibt sich folgende Gleichung:
Die gespiegelten Punkte haben also folgende Koordinaten:
Als letztes muss noch der Trägergraph bestimmt werden.
In Koordinatenform dargestellt ergibt sich:
Dazu löst man die Gleichung (1) nach auf.
Setze nun Gleichung in ein:
Die gespiegelte Gerade hat demnach folgende Gleichung:
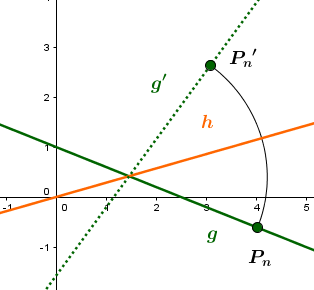
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung einer Geraden an einer Ursprungsgeraden
Somit ergibt sich folgende Gleichung:
Die gespiegelten Punkte haben also folgende Koordinaten:
Als letztes muss noch der Trägergraph bestimmt werden.
In Koordinatenform dargestellt ergibt sich:
Dazu löst man die Gleichung (1) nach auf.
Setze nun die Gleichung in ein:
Die gespiegelte Gerade hat demnach folgende Gleichung:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung einer Gerade an einer Ursprungsgerade
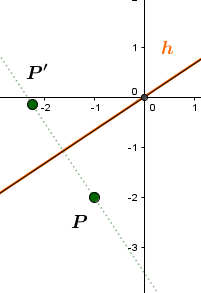
Die Gerade soll an der Geraden gespiegelt werden:
Das heißt, man wählt sich einen beliebigen Punkt auf der Geraden g und spiegelt diesen an der Geraden auf den Bildpunkt .
ist somit ein beliebiger Punkt auf der Bildgeraden .
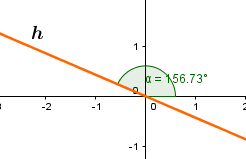
Um den Punkt an der Geraden zu spiegeln, benötigt man als erstes den Winkel , den die Gerade mit der x-Achse einschließt.
Somit ergibt sich folgende Gleichung:
Die gespiegelten Punkte haben also folgende Koordinaten:
Als letztes muss noch der Trägergraph bestimmt werden.
In Koordinatenform dargestellt ergibt sich:
Dazu löst man die Gleichung (1) nach auf.
Setze nun die Gleichung in ein:
Die gespiegelte Gerade hat demnach folgende Gleichung:
- 4
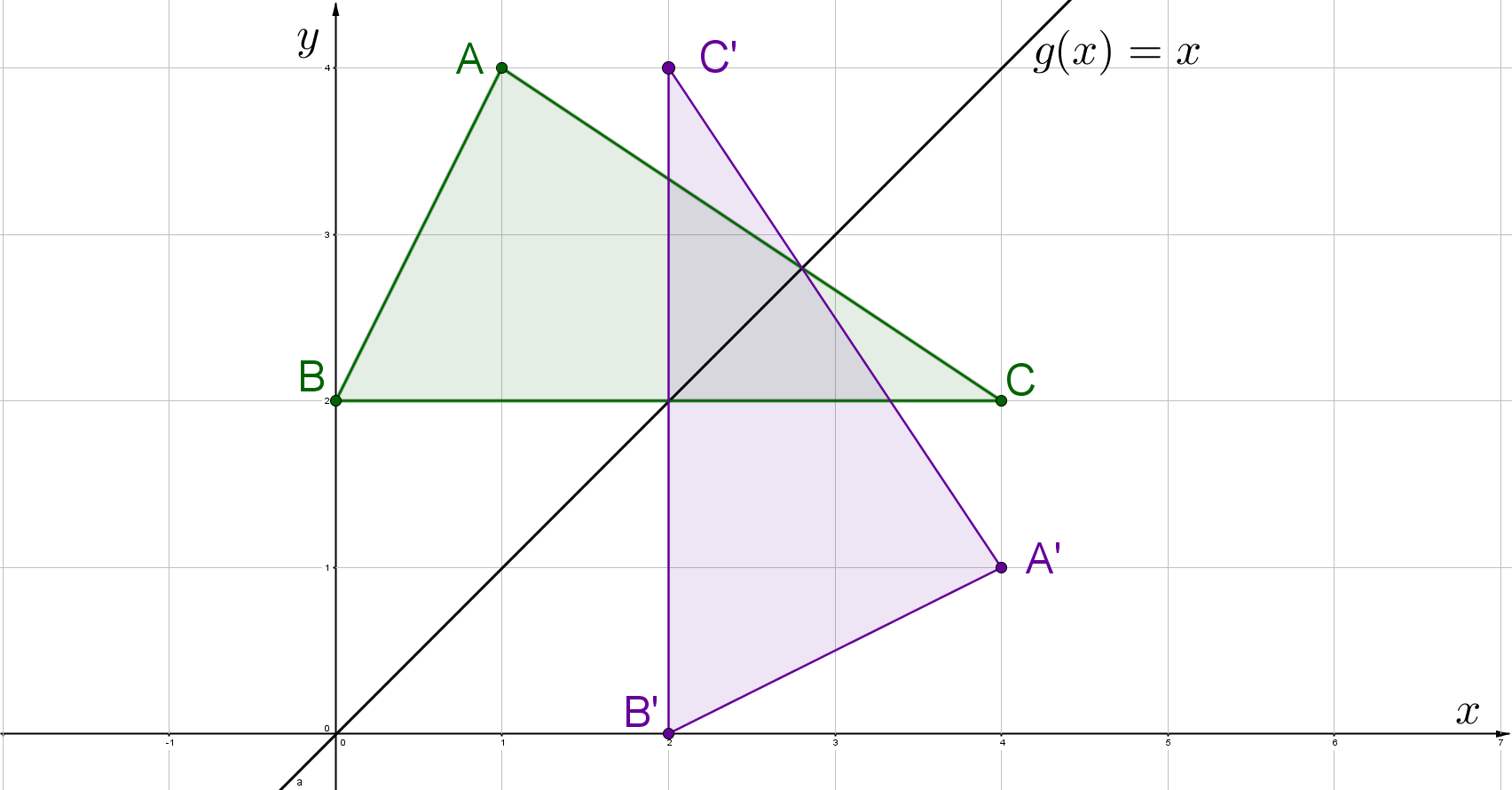
Spiegele das Dreieck gegeben durch die Punkte , , an der Gerade und berechne die Koordinaten der Bildpunkte .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung an einer Ursprungsgeraden
Die Steigung der Geraden ist . Das bedeutet, dass der Winkel ist.
Variante 1: Berechnung in Koordinatenform:
Die Koordinaten der gespiegelten Punkte erhältst du mit:
Setze den Winkel nun ein.
Setze die Koordinaten der Punkte , und jetzt in diese Formeln ein und berechne das Ergebnis:
Variante 2: Berechnung in Matrixform:
↓ Setze den WInkel in die Matrix ein.
↓ Berechne die Werte des Sinus und Cosinus.
Setzt nun die Koordinaten der Punkte und ein und führe die Matrix-Vektor-Multiplikationen durch:
- 5
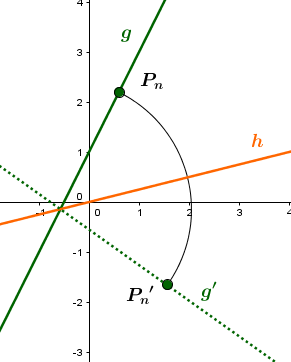
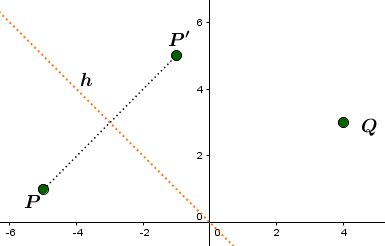
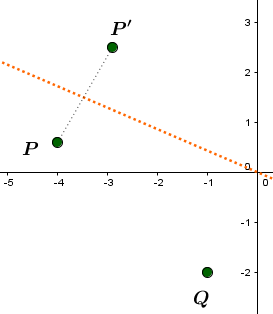
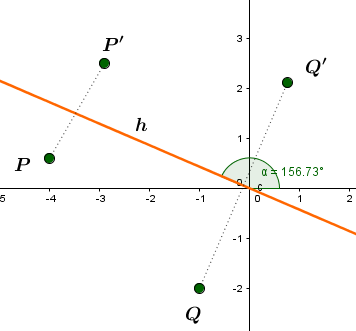
Der Bildpunkt entsteht durch Spiegelung des Urpunktes an einer Ursprungsgeraden .Gib die Gleichung der Spiegelachse , die Abbildungsgleichung und die Koordinaten von an.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelachse berechnen
Skizze:
Um die Gleichung der Spiegelachse zu bestimmen, musst du zuerst den Schnittwinkel der Spiegelachse mit der x-Achse berechnen. Dazu benuzt du die Abbildungsgleichung, setzt und ein und löst nach auf.
Hier bietet sich die Koordinatenform an:
Setze in ein und löse nach auf.
Du hast also den Winkel bestimmt, unter dem sich die Spiegelachse mit der x-Achse schneidet.
Mit dieser Information kannst du auf die Steigung der Geraden schließen und somit die Geradengleichung aufstellen.
Nachdem du die Gleichung der Spiegelachse bestimmt hast, musst du noch die Abbildungsgleichung und den Bildpunkt angeben bzw. berechnen.
Abbildungsgleichung in Koordinatenform:
Spiegelung von
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelachse berechnen
Skizze:
Um die Gleichung der Spiegelachse zu bestimmen, musst du zuerst den Schnittwinkel der Spiegelachse mit der x-Achse berechnen. Dazu benuzt du die Abbildungsgleichung, setzt und ein und löst nach auf.
Hier bietet sich die Koordinatenform an:
Setze in ein und löse nach auf.
in :
Du hast also den Winkel bestimmt, unter dem sich die Spiegelachse mit der x-Achse schneidet.
Mit dieser Information kannst du auf die Steigung der Geraden schließen und somit die Geradengleichung aufstellen.
Nachdem du die Gleichung der Spiegelachse bestimmt hast, musst du noch die Abbildungsgleichung und den Bildpunkt angeben bzw. berechnen.
Abbildungsgleichung in Koordinatenform:
Spiegelung von
Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelachse berechnen
Skizze:
Um die Gleichung der Spiegelachse zu bestimmen, musst du zuerst den Schnittwinkel der Spiegelachse mit der x-Achse berechnen. Dazu benuzt du die Abbildungsgleichung, setzt und ein und löst nach auf.
Hier bietet sich die Koordinatenform an:
Setze in ein und löse nach auf.
in :
Du hast also den Winkel bestimmt, unter dem sich die Spiegelachse mit der x-Achse schneidet.
Mit dieser Information kannst du auf die Steigung der Geraden schließen und somit die Geradengleichung aufstellen.
Nachdem du die Gleichung der Spiegelachse bestimmt hast, musst du noch die Abbildungsgleichung und den Bildpunkt angeben bzw. berechnen.
Abbildungsgleichung in Koordinatenform:
Spiegelung von