Teil B
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen
Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe B 1
Manchmal werden zu Fasching Krapfen zum
Spaß mit Senf gefüllt. Von zwölf Krapfen sind
zwei mit Senf („S“) und zehn mit Marmelade
(„M“) gefüllt.
Martin nimmt sich von den zwölf Krapfen zwei
zufällig ausgewählte.

Zeichnen Sie ein zugehöriges Baumdiagramm, in dem alle Anteile ersichtlich sind.
(2,5 P)
Berechnen Sie die Wahrscheinlichkeit dafür, dass mindestens einer der beiden
ausgewählten Krapfen mit Senf gefüllt ist. (2 P)
Ergebnis:
Martin vermutet, dass mit einer Wahrscheinlichkeit von mehr als keiner der
beiden ausgewählten Krapfen mit Senf gefüllt ist.
Beurteilen Sie diese Vermutung. (2 P)
- 2
Aufgabe B 2
Die Vorlage einer Spielfigur ist ein Rotationskörper mit der Rotationsachse MS. Nebenstehende Skizze zeigt grau eingefärbt den zugehörigen Axialschnitt.
Es gilt: ;
.
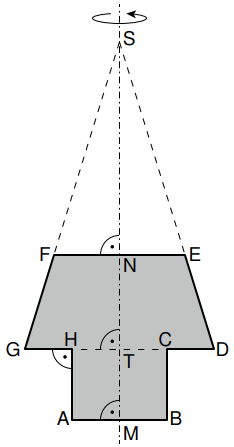
Berechnen Sie das Volumen des Rotationskörpers.
Runden Sie auf zwei Stellen nach dem Komma.
Zwischenergebnis: (4 P)
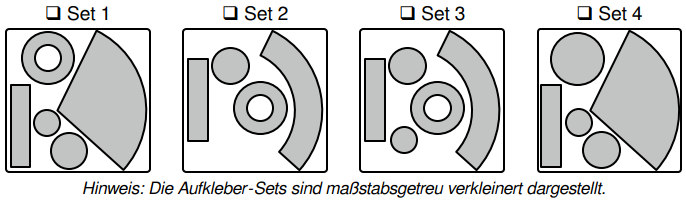
Die komplette Oberfläche der Spielfigur soll mit einer grauen Schutzfolie beklebt werden.
Welches Aufkleber-Set ist hierfür passend? Kreuzen Sie an. (1 P)
- 3
Aufgabe B3
Die Parabel mit dem Scheitelpunkt verläuft durch den Punkt .
Sie hat eine Gleichung der Form mit und .
Die Gerade hat die Gleichung mit .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Zeigen Sie durch Rechnung, dass für die Gleichung der Parabel gilt:
.
Zeichnen Sie sodann die Parabel sowie die Gerade für in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit ; (5 P)
Punkte auf der Parabel und Punkte auf der Geraden haben dieselbe Abszisse . Sie sind für zusammen mit Punkten die Eckpunkte von Dreiecken . Die Punkte liegen ebenfalls auf der Geraden und ihre Abszisse ist stets um kleiner als die Abszisse der Punkte .
Zeichnen Sie die Dreiecke für und für in das Koordinatensystem zu Aufgabe a) ein. (2 P)
Zeigen Sie rechnerisch, dass für die Länge der Strecken in Abhängigkeit von gilt: . (1 P)
Unter den Strecken hat die Strecke die maximale Länge.
Berechnen Sie die Länge der Strecke sowie den zugehörigen Flächeninhalt des Dreiecks . (2,5 P)
In allen Dreiecken haben die Winkel das gleiche Maß.
Berechnen Sie das zugehörige Maß .
Ergebnis: (1,5 P)
Unter den Dreiecken gibt es die gleichschenkligen Dreiecke mit der Basis sowie mit der Basis .
Begründen Sie rechnerisch, dass die Länge der Schenkel bei diesen gleichschenkligen Dreiecken stets beträgt.
Berechnen Sie anschließend die zugehörigen Werte für . (3 P)
- 4
Aufgabe 4
Die nebenstehende Skizze zeigt das Fünfeck sowie den Kreisbogen mit dem Mittelpunkt und dem Radius .
Es gilt: ; ;
; ;
; .
Runden Sie im Folgenden auf zwei Stellen
nach dem Komma.
Zeichnen Sie das Fünfeck mit den Strecken und sowie den Kreisbogen . (3 P)
Begründen Sie, dass gilt: .
Berechnen Sie sodann die Maße der Winkel und sowie die Länge der Strecke .
Teilergebnisse: ; (4 P)
Berechnen Sie den Umfang der Figur, die durch die Strecken , , sowie den Kreisbogen begrenzt wird.
Zwischenergebnis: (4 P)
Ein Kreis um Punkt berührt die Strecke im Punkt und schneidet die Strecke im Punkt sowie die Strecke im Punkt .
Ergänzen Sie die Zeichnung zu Aufgabe a) um die Strecke und den Kreisbogen mit dem Mittelpunkt .
Bestimmen Sie sodann rechnerisch die Länge der Strecke und den Flächeninhalt des Sektors, der durch die Strecken und sowie den Kreisbogen begrenzt wird.
Teilergebnisse: (3 P)
Bestimmen Sie rechnerisch den prozentualen Anteil des Flächeninhalts des Sektors aus Aufgabe d) am Flächeninhalt des Dreiecks . (2 P)







