Konstruktion regulärer n-Ecke

Dieser Artikel beschreibt die Konstruktion von regulären n-Ecken, insbesondere eines regulären Dreiecks, Vierecks und Sechsecks. Mit Konstruktion ist gemeint, dass die Figuren allein mit der Verwendung von Zirkel und Lineal gezeichnet werden.

Konstruktion eines regulären Dreiecks

Im Folgenden soll ein reguläres Dreieck (= gleichseitiges Dreieck) mit der Seitenlänge $c$ konstruiert werden.

Mit dem Schieberegler kann man sich die Konstruktion Schritt für Schritt anzeigen lassen.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.

Konstruktion eines Quadrats (reguläres Viereck)

Im Folgenden soll ein reguläres Viereck (= Quadrat) mit der Seitenlänge $a$ konstruiert werden.

Mit dem Schieberegler kann man sich die Konstruktion Schritt für Schritt anzeigen lassen.

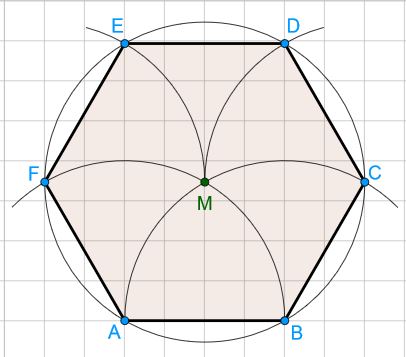
Konstruktion eines regulären Sechsecks

Hier wird nun das reguläre Sechseck (auch Hexagon genannt) konstruiert. Mit dem Schieberegler kann man sich die Konstruktion Schritt für Schritt anzeigen lassen.

Welche regulären $n$ -Ecke sind konstruierbar?

Nicht jedes reguläre $n$ -Eck kann mithilfe des Zirkels und Lineals konstruiert werden. Die Formel

n = 2^{(2^{k})} + 1

liefert eine Auswahl von konstruierbaren $n$ - Ecken. Beispiele hier für sind:

$2^{(2^{0})} + 1 = 3$
$2^{(2^{1})} + 1 = 5$
$2^{(2^{2})} + 1 = 17$
$2^{(2^{3})} + 1 = 257$

Zusätzlich kommt mit $n = 4$ das regelmäßige Viereck hinzu und weiter alle Zahlen, die durch Verdoppelung gewonnen werden können. Somit sind auch $6$ -Ecke, $10$ -Ecke etc. konstruierbar, aber nicht etwa ein $7$ -Eck oder ein $11$ -Eck.