Analysis, Teil A, Aufgabengruppe 2

1. Nullstellen berechnen

Die Nullstellen von $f$ sind die Nullstellen des Zählers, wenn diese ungleich $-2$ sind ($-2$ ist nicht in ${𝔻}_{𝕗}$ enthalten).

$\Rightarrow x^2-9=(x+3)\cdot (x-3)=0$

Verwende den Satz vom Nullprodukt:

$\Rightarrow x+3=0\Rightarrow x_1=-3$ und $x-3=0\Rightarrow x_2=+3$

Die Funktion $f$ hat die beiden Nullstellen $x_1=-3$ und $x_2=+3$.

Koordinaten des Schnittpunkts des Graphen von $f$ mit der y-Achse

Berechne $f(0)$:

$\Rightarrow f(0)={\displaystyle \frac{0^2-9}{0+2}}={\displaystyle \frac{-9}{2}}=-\mathrm{4,5}$

Es ist$${\displaystyle \underset{x\to -\infty }{\lim }{\displaystyle \frac{\stackrel{\to +\infty }{\overbrace{x^2-9}}}{\underset{\to -\infty }{\underbrace{x+2}}}}=-\infty }$$ und $${\displaystyle \underset{x\to +\infty }{\lim }{\displaystyle \frac{\stackrel{\to +\infty }{\overbrace{x^2-9}}}{\underset{\to +\infty }{\underbrace{x+2}}}}=+\infty }$$

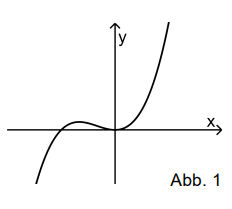
Term der ersten Ableitungsfunktion von $g$

Gegeben ist die Funktion $g(x)=x^3+x^2$.

Berechne die 1. Ableitung einer Potenzfunktion:

Inhalt der Fläche, die der Graph von $g$ mit der x-Achse einschließt

Dazu werden die Nullstellen von $g$ benötigt.

$g(x)=x^3+x^2=x^2(x+1)\Rightarrow x^2(x+1)=0$

Die Lösungen erhält man mit dem Satz vom Nullprodukt:

$x^2=0\Rightarrow x_{\mathrm{1,2}}=0$ und $x+1=0\Rightarrow x_3=-1$

Berechne nun das Integral:

Antwort: Der Inhalt der Fläche, die der Graph von $g$ mit der x-Achse einschließt, beträgt ${\displaystyle \frac{1}{12}}\text{FE}$.

Wie geht der Graph von $h$ aus dem Graphen der Funktion $w$ hervor?

Es ist $w(x)=\sqrt{x}$ und $h(x)=\sqrt{x+3}-2$.

$w\stackrel{\stackrel{}{\text{Verschieb. um 3 auf der x-Achse nach links}}}{\to }\sqrt{x+3}\stackrel{\stackrel{}{\text{Verschieb. um 2 in Richtung der y-Achse nach unten}}}{\to }\underset{h(x)}{\underbrace{\sqrt{x+3}-2}}$

Als Hilfe kannst du die Graphen von $w$ und $h$ zeichnen:

Antwort: Der Graph von $h$ entsteht aus $w$ durch Verschiebung um 3 nach links und um 2 nach unten.

Begründen Sie, dass h umkehrbar ist

Alle streng monoton wachsenden bzw. streng monoton fallenden Funktionen besitzen eine Umkehrfunktion.

Die Funktion $h$ ist streng monoton wachsend, besitzt also eine Umkehrfunktion.

Beschreiben Sie, wie der Graph der Umkehrfunktion $h^{-1}$ von $h$ aus dem Graphen von $h$ hervorgeht

$h\stackrel{\stackrel{}{\text{Spiegelung an der Winkelhalbierenden y=x}}}{\to }{h}^{-1}$

Geben Sie den Definitions- und den Wertebereich von $h^{-1}$ an

Beim Umkehren vertauschen sich Definitions- und Wertemenge. Die Definitionsmenge von $h$ ist die Wertemenge von $h^{-1}$ und die Wertemenge von

$h$ ist die Definitionsmenge von $h^{-1}$.

Es ist ${𝔻}_{𝕙}=\{x\in ℝ|x\ge -3\}$ und ${𝕎}_{𝕙}=\{y\in ℝ|y\ge -2\}$.

Demnach ist dann ${𝔻}_{{𝕙}^{-\mathrm{𝟙}}}=\{x\in ℝ|x\ge -2\}$ und ${𝕎}_{{𝕙}^{-\mathrm{𝟙}}}=\{y\in ℝ|y\ge -3\}$.

Gleichung der Tangente t

$t:y=m\cdot x+b$

Der y-Achsenabschnitt ist $b=-8$ (Schnitt von $t$ mit der y-Achse) und mit dem eingezeichneten Steigungsdreieck erhält man $m={\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}}={\displaystyle \frac{16}{4}}=4$.

Also ist $t:y=4\cdot x-8$.

Tangente an den Graphen von $f_a$ im Punkt $(u|f_a(u))$ schneidet die y-Achse im Punkt $(0|-f_a(u))$

Es ist $f_a(x)=a{x}^2\Rightarrow f_a^{\prime }(x)=2ax$ und der Punkt ist $(u|f_a(u))$.

Weiterhin gilt für die Tangente:

Setze die Koordinaten von $(u|f_a(u))$ in $t:y=2au\cdot x+b$ ein:

Mit $f_a(u)=a{u}^2$ folgt dann $b=a{u}^2-2a{u}^2=-a{u}^2$.

Damit erhält man für die Tangentengleichung im Punkt $(u|f_a(u))$:

Für den Schnittpunkt der Tangente $t$ mit der y-Achse setze $x=0$ in $t$ ein. Mit $x=0$ folgt $y=-a{u}^2=-f_a(u)$.

Also ist: