Weitere Aufgaben zu Extremwertproblemen
Hier findest du Aufgaben zu Extremwertproblemen. Lerne das Optimieren mithilfe von Extremwertproblemen!
- 1
Welcher Punkt auf der Geraden g mit der Funktionsgleichung hat vom Punkt minimalen Abstand?
Wie groß ist dieser minimale Abstand?
Fertige zunächst eine Skizze an!
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe lösen
Abstand eines Punktes von einer Geraden
Bei dieser Aufgabe bestimmst du als Extremwertaufgabe denjenigen Punkt der Geraden, der von einem gegebenen Punkt außerhalb der Geraden den kleinsten Abstand hat.
Der Zeichnung entnimmst du die Zielfunktion und die Nebenbedingung dieser Extremwertaufgabe.
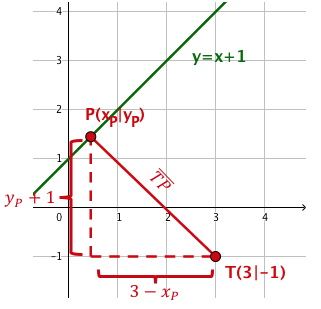
Zielfunktion
Abstand der Punkte und .
Nebenbedingung
Der Punkt liegt auf der Geraden
Berechne die Zielfunktion mit Hilfe des Satzes des Pythagoras.
↓ Setze die Geradengleichung für y ein.
↓ Quadriere aus
↓ Fasse zusammen
↓ Ziehe die Wurzel
Beachte für Extremwertaufgaben mit einer Abstandsbedingung:
Für alle Punkte, für die der Abstand minimal oder maximal wird, ist auch das Quadrat des Abstandes minimal bzw. maximal, da gilt:
.
Da die Ableitung für bequemer zu berechnen ist, als für (keine Wurzel!), benutzt man als Zielfunktion ab hier das Quadrat des Abstandes.
↓ Bilde die Ableitung
↓ Setze die Ableitung gleich Null
Berechne die 2. Ableitung der Zielfunktion, um dich zu versichern, dass ein Minimum des Quadrats des Abstandes liefert.
Bestimme jetzt aus der Nebenbedingung :
ist der gesuchte Punkt.
Berechne abschließend , nicht nur !!
Ergebnis:
Der minimale Abstand des Punktes von der Geraden beträgt:
Alternative Lösung
Ohne Kenntnisse aus der Differenzialrechnung kannst du die Aufgabe auch mit einer geometrischen Überlegung lösen:
Der gesuchte Punkt der Geraden mit kleinstem Abstand zum Punkt ist der Lotfußpunkt vom Punkt auf die Gerade .
Er kann
a) als Gleitpunkt auf der Geraden oder
b) als Schnittpunkt zweier Geraden
berechnet werden.
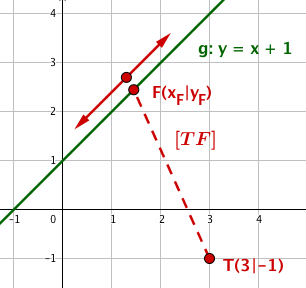
a) Der Lotfußpunkt als Gleitpunkt auf .
Wenn die Strecke auf der Geraden senkrecht stehen soll, muss für deren Steigungen und gelten:
.
Also:
↓ Setze die Geradengleichung für y ein
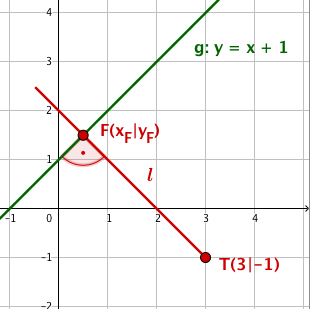
b) Der Lotfußpunkt liegt auf der Geraden , seine x-Koordinate hast du gerade berechnet, die y-Koordinate erhältst du durch einsetzen in :
Im nachfolgenden Applet kannst du die Rechnung überprüfen, indem du den Geradenpunkt verschiebst.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung. - 2
Welcher Punkt P auf der Parabel mit der Funktionsgleichung hat vom Punkt minimalen Abstand?
Wie groß ist dieser minimale Abstand?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben
Der Zeichnung entnimmst du die Zielfunktion und die Nebenbedingung dieser Extremwertaufgabe.
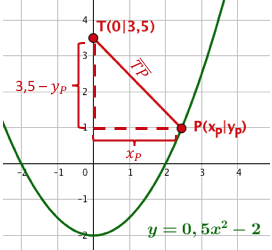
Zielfunktion:
Abstand der beiden Punkte und .
Nebenbedingung:
Der Punkt liegt auf der Parabel.
Gib die Zielfunktion an. Benutze dazu den Satz des Pythagoras.
Gib die Funktionsgleichung der Nebenbedingung an.
Beachte: Für alle Punkte, für die der Abstand minimal wird, wird auch das Quadrat des Abstandes minimal.Deshalb nimmt man als Zielfunktion.
Dies erleichtert die Rechnung.
Zielfunktion:
Nebenbedingung:
Setze die Nebenbedingung in die Zielfunktion ein.
Fasse in der Klammer zusammen und quadriere mit der binomischen Formel.
Bilde die Ableitung
Setze die Ableitung gleich Null und löse die Gleichung.
Untersuche, für welche der Lösungen die 2. Ableitung positiv ist, damit jeweils ein Minmum vorliegt
ergibt ein lokales Maximum des Abstandsquadrats.
und liefern ein Minimum des Quadrat des Abstandes und damit auch ein Minimum des Abstands.
Gib die drei Punkte und den dazu gehörigen Abstand an.
Einsetzen der drei -Werte in die Nebenbedingung:
und
Ergebnis:
Die beiden Punkte und haben von der Parabel mit rund den geringsten Abstand.
Im nachfolgenden Applet kannst du dies überprüfen indem du den Punkt verschiebst.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.Alternative Lösung
Bei dieser Lösung ermittelst du in Frage kommende Parabelpunkt über eine Betrachtung von Tangenten der Parabel.
Für die drei Extremumspunkte , , gilt:
Die jeweilige Verbindungsstrecke zum Punkt steht senkrecht auf der Parabeltangente.
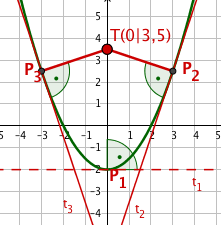
Parabel:
Tangentensteigung:
Gib die Steigung von an.
Lotbedingung ansetzen!
Damit sind - auf anderem Weg - die x-Koordinaten der beiden Lösungspunkte der Extremumsaufgabe gefunden.
Zusatz:
Auch für den Punkt ("Maximumspunkt") steht die Tangente senkrecht auf der Verbindungsstrecke zu .
Bei dieser Aufgabe sollst du den minimalen Abstand eines Parabelpunktes von einem vorgegebenen Punkt "innerhalb" der Parabel als Extremwertaufgabe berechnen.
- 3
Der Absatz (Verkaufszahlen) einer Ware ist wesentlich abhängig vom Preis . Je höher der Preis, desto geringer ist in der Regel der Absatz.
Diesen Zuammenhang beschreibt die Preis-Absatz-Funktion (PAF)
Der Umsatz (Verkaufserlös) ist als Produkt aus Absatz und Preis eine Wertgröße.
Eine Firma verkauft pro Monat von einem Artikel Stück zu einem Stückpreis von .
Die Preis-Absatz-Funktion ist gegeben durch:
Bestimme den monatlichen Umsatz in Abhängigkeit vom Stückpreis p.
Für welchen Preis p ist der Umsatz maximal?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
In dieser Aufgabe aus dem Wirtschaftsleben sollst du den Zusammenhang zwischen Warenpreis und Verkaufserfolg, der am Umsatz gemessen wird, erfassen und den maximalen Umsatz als Extremwertaufgabe berechnen.
Anmerkung: Diese Lösungsskizze rechnet ohne Einheiten.
Gesucht: und optimaler Preis
Stelle die Zielfunktion auf: monatlicher Umsatz = Stückzahl mal Preis.
Erkenne die Nebenbedingung, die durch die Preis-Absatz-Funktion gegeben ist.
:
Bestimme die Extremalfunktion , also den monatlichen Umsatz in Abhängigkeit vom Preis, indem du in die Nebenbedingung einsetzt.
Berechne die erste und zweite Ableitung.
Setze die erste Ableitung gleich Null und erkenne anhand der zweiten Ableitung, dass es sich um ein Maximum handelt.
Berechne .
Ergebnis:
Der maximale monatliche Umsatz der Firma beim Verkauf des Artikels beträgt bei einem Stückpreis von .
- 4
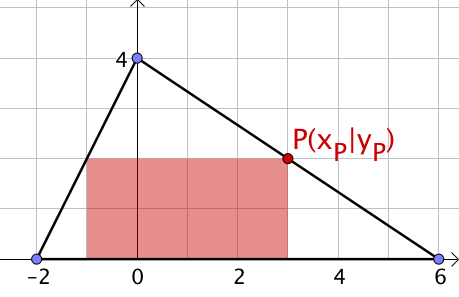
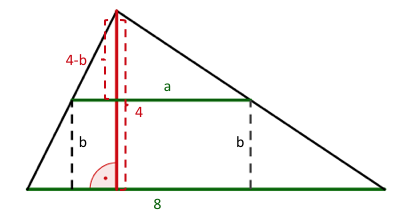
Dem abgebildeten Dreieck soll ein Rechteck mit möglichst großem Flächeninhalt einbeschrieben werden.
Berechne den größtmöglichen Flächeninhalt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Bei dieser Aufgabe ist einem Dreieck ein größtmögliches Rechteck einzubeschreiben. Es handelt sich also um eine Extremwertaufgabe
Wenn du eine Rechtecksseite auf die Grundlinie des Dreiecks legst, bedeutet die Forderung des "Einbeschreibens", dass die beiden weiteren Rechteckspunkte und jeweils auf den anderen Seiten des Dreiecks liegen. Dies ergibt zwei Nebenbedingungen für die Extremwertaufgabe.
Da der Flächeninhalt maximiert werden soll, benötigst du zunächst als Zielfunktion die Formel für den Flächeninhalt eines Rechtecks, in die du dann die Nebenbedingungen "einarbeiten" musst.
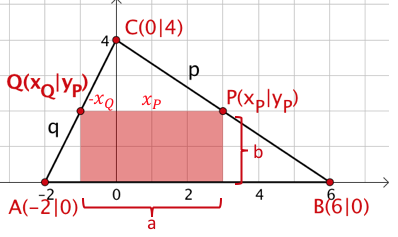
Zielfunktion
mit und also:
1. Nebenbedingung
liegt auf der Geraden .
Stelle die Gleichung der Geraden mit Hilfe der Punkte und auf.
Gib nun die 2. Nebenbedingung an.
2. Nebenbedingung
liegt auf der Geraden .
Stelle die Gleichung der Geraden mit Hilfe der Punkte und auf.
Löse nach auf.
↓ Setze für den Term aus (1) ein.
↓ Multipliziere die Klammer aus
Setze und in die Zielfunktion ein, um die Zielfunktion in Abhängigkeit der einzigen Variablen zu erhalten.
↓ Multipliziere aus
Bilde die Ableitung .
Setze gleich Null und löse die Gleichung.
Überprüfe mit der 2. Ableitung, ob sich für tatsächlich ein Maximum ergibt.
ist eine konstante Funktion. Somit ist auch und ergibt eine größtmögliche Rechtecksfläche.
Setze in die Fläche ein.
Flächeninhalt:
Setze auch noch in die 1. Nebenbedingung ein, um die 2. Koordinate des Eckpunktes P zu erhalten.
Nebenbedingung:
Ergebnis:
Mit dem Eckpunkt ist das größtmögliche Rechteck in das Dreieck einbeschrieben und hat den Flächeninhalt .
Alternative Lösung 1
Der Graph der Zielfunktion
ist eine nach unten geöffnete Parabel.
Ihr Maximum ist der Scheitelpunkt. Diesen kann man - außer über die Ableitung von - durch eine quadratische Ergänzung ermitteln.
↓ Klammere aus.
↓ ↓ 2. binomische Formel benutzen.
Lies den Scheitelpunkt ab
Dessen 2. Koordinate liefert den gesuchten maximalen Flächeninhalt eines dem Dreieck einbeschriebenen Rechtecks.
Im nachfolgenden Applet kannst du durch Verschieben des Punktes P das Ergebnis kontrollieren.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.Alternative Lösung 2
Die gestellte Aufgabe lässt eine verblüffend einfache Lösung zu. Dabei wird das Koordinatensystem nicht benötigt, sondern sie ergibt sich aus dem Strahlensatz.
Entscheidend für diese Möglichkeit ist, dass vom Dreieck neben der Grundlinie die Höhe auf diese Seite mit gegeben ist.
Zielfunktion ist die Formel für die Fläche des Rechtecks mit den Seitenlängen und . Also:
Die Nebenbedingung ergibt sich aus dem Strahlensatz.
Benutze den Strahlensatz und erhalte:
Setze in ein.
Die Zielfunktion ist eine nach unten geöffnete Parabel. Deshalb ergibt die y-Koordinate des Scheitelpunktes den maximal möglichen Flächeninhalt einbeschriebener Rechtecke.
Den Scheitelpunkt berechnest du über die Ableitung von oder mit einer quadratischen Ergänzung.
Ableitung von
quadratische Ergänzung
Vertiefung der Aufgabe
In der gegebenen Aufgabenstellung soll das Rechteck dem Dreieck so einbeschrieben werden, dass eine Rechteckseite auf der Grundseite liegt.
Natürlich kann man Rechtecke auch so einbeschreiben, dass eine Rechteckseite auf einer der beiden anderen Dreieckseiten liegt.
Dann stellt sich die Frage: Haben die maximal möglichen Flächeninhalte auch bei den beiden anderen Lagen den gleichen Wert?
Dass dies tatächlich so ist, kannst du am folgenden Applet nachvollziehen, indem du die unterschiedlichen Gleitpunkte , oder verschiebst.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung. - 5
Es gibt viele Zahlenpaare positiver Zahlen, deren Produktwert 0,64 beträgt.
a) Gib 10 solcher Zahlenpaare an.
b) Ermittle dasjenige Zahlenpaar, das den kleinsten Summenwert besitzt.
Teilaufgabe a
Für diese Teilaufgabe gibt es viele Lösungen. Du kannst zum Beispiel diese 10 Zahlenpaare angeben:
(0,1|6,4), (0,8|0,8), (1|0,64), (2|0,32), (4|0,16), (8|0,08), (10|0,064), (16|0,04), (32|0,02), (64|0,01).
Teilaufgabe b
Ein allgemeines Zahlenpaar kannst du schreiben als mit zwei Zahlen und , die du noch bestimmen musst.
Da nach jenem Zahlenpaar gesucht ist, dass den kleinsten Summenwert besitzt, musst du die Funktion unter der Nebenbedingung minimieren.
Löst du die Nebenbedingung nach auf, so erhältst du den Zusammenhang
den du in die Funktion einsetzen kannst. Das bedeutet:
Gesucht ist also das Minimum dieser Funktion. Kandidaten für Extremstellen von sind als Nullstellen von gegeben. Die erste Ableitung von berechnet sich zu
Setzt du das eben berechnete gleich null, so erhältst du als Lösungen
Da nach einem Zahlenpaar positiver Zahlen gesucht ist, kannst du die negative Lösung vernachlässigen. Um die Art des Extremums zu verifizieren (gesucht ist ja ein Minimum), berechnest du die zweite Ableitung. Sie ist gegeben durch
Setzt du in ein, erkennst du, dass
gilt, sodass bei tatsächlich ein Minimum von vorliegt.
Setzt du in die Nebenbedingung ein, so erhältst du
Das gesuchte Zahlenpaar ist also .
- 6
Aus einer rechteckigen Fensterscheibe mit den Seitenlängen und , ist vom unteren Mittelpunkt der kleineren Seite aus, eine Ecke geradlinig unter einem Winkel von 45° abgesprungen.
Aus der restlichen Scheibe soll durch Schnitte parallel zu den ursprünglichen Seiten eine möglichst große rechteckige Scheibe hergestellt werden.
Welche Seitenlängen und welche Fläche hat die "Ersatzscheibe"? In welchem Punkt setzen die Schnitte an?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben
Bei dieser Aufgabe soll ein größtmöglicher Flächeninhalt bestimmt werden. Es handelt sich also um eine Extremwertaufgabe.
Die Scheibe sei höher als breit. Also gelte: .
Das abgeschnittene Stück der Scheibe ist wegen des Neigungswinkels von 45° ein gleichschenklig-rechtwinkliges Dreieck mit der Kathetenlänge von .
Die gesuchte rechteckige "Ersatzscheibe" habe die Seitenlängen und und entsteht von einem Punkt aus, der auf der abgebrochenen Schnittkante variiert.
Die Zielfunktion ist der Flächeninhalt eines Rechtecks mit den Seiten und :
,
wobei
und
Grafische Veranschaulichung
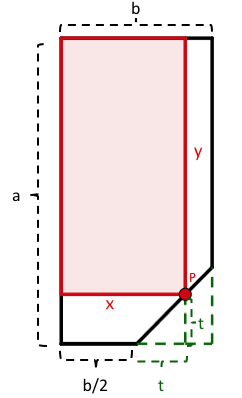
Die Nebenbedingungen für ergeben sich aus dessen variabler Lage auf der Schnittkante und können mit einem variablen Parameter so angegeben werden:
Setze die Nebenbedingungen in die Zielfunktion ein, um diese als Funktion der Variablen zu erhalten.
Zielfunktion
↓ Bilde - z.B. mit der Produktregel - die 1. Ableitung und die 2. Ableitung .
↓ Setze gleich Null und löse die Gleichung.
Zwischenstand der Lösung:
Die gesuchte Ersatzscheibe mit maximalem Flächeninhalt wird von einem variablen Punkt P aus erzeugt, der auf der Strecke liegen muss.
Damit ist der Definitionsbereich der Flächen-Zielfunktion auf das Intervall begrenzt.
ist wegen eine nach unten geöffnete Parabel und der errechnete Wert liefert ein lokales Maximum - also einen maximalen Flächeninhalt, aber nur dann, wenn der Wert im Intervall liegt.
Da ist jedenfalls .
ist aber nicht für jedes Zahlenpaar und kleiner als , da gilt:
Fallunterscheidung:
Fall 1: ("a nicht zu groß")
Fall 2:("a beliebig groß")
Setze in ein.
Fall 1:
liefert lokales Maximum
Die Seitenlängen der Ersatzscheibe sind:
Die Ersatzscheibe ist demnach ein Quadrat.
Für den Punkt auf , von dem aus geschnitten wird gilt:
Zahlenbeispiel
Am nachfolgenden Applet kannst du die Aufgabe mit den Zahlenwerten und nachvollziehen. Verschiebe dazu den Erzeugungspunkt längst der Bruchkante .
Man erhält für den maximalen Flächeninhalt , für die (quadratische) Rechtecksseite und für den Abstand des Punktes von den Wert
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.Fall 2
Damit liegt der Scheitelpunkt der Flächenparabel rechts vom Intervall und nimmt in diesem Intervall streng monoton zu.
Die größte Fläche wird demnach - als Randextremum - angenommen, wenn der erzeugende Punkt mit dem rechtem Randpunkt zusammenfällt. Also für .
Demnach gilt hier:
.
Die Seitenlängen für sind:
und .
Für den erzeugenden Punkt gilt: .
Zahlenbeispiel
Am nachfolgenden Applet kannst du die Aufgabe mit den Zahlenwerten und nachvollziehen. Verschiebe dazu den Erzeugungspunkt längs der Bruchkante .
Man erhält für den maximalen Flächeninhalt , bei den Seitenlängen von und .
Zusammenfassung
Die Aufgabe ist durch die notwendige Fallunterscheidung der Fenstermaße anspruchsvoll.
Falls die Fensterhöhe "nicht zu groß" gegenüber der Fensterbreite ist (), besitzt die Aufgabe ein lokales Maximum.
Falls die Fensterhöhe "zu groß" gegenüber der Fensterbreite ist () ergibt sich ein Randmaximum.
Alternative Lösung
Die beschriebene Lösung hat für die variable Lage des Erzeugungspunktes auf der Bruchkante seinen horizontalen Abstand vom Punkt als Parameter verwendet.
Für eine alternative Lösung der Aufgabe verzichten wir auf einen zusätzlichen Parameter und betrachten die Rechtecksseiten und als die Variablen des gesuchten maximalen Rechtecks und bestimmen die Nebenbedingung zwischen und aus dem Strahlensatz.
Die Zielfunktion lautet:
mit
Die Nebenbedingung ergibt sich durch Anwendung des Strahlensatzes in der nebenstehenden Skizze:
Grafische Veranschaulichung
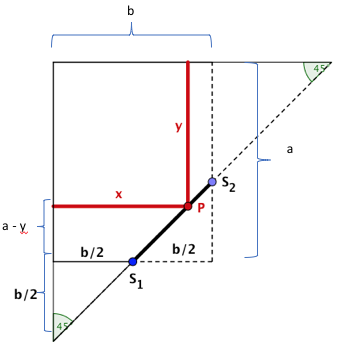
Setze das Ergebnis der Nebenbedingung in die Zielfunktion ein.
↓ Setze gleich Null, um ein mögliches Maximum zu erhalten.
↓ mit
Zwischenstand der alternativen Lösung
Die gesuchte Ersatzscheibe mit maximalem Flächeninhalt ist ein Rechteck mit den Seitenlängen und .
Dabei muss eine Zahl aus dem Intervall sein, damit der erzeugende Punkt auf der Strecke liegt.
Durch die Nebenbedingung aus dem Strahlensatz ergibt sich mit eine nach unten geöffnete Parabel und liefert ein lokales Maximum für die Rechtecksfläche - aber nur dann, wenn im Intervall liegt.
Da gilt: , ist jedenfalls
.
ist aber nicht für jedes Zahlenpaar und kleiner als , da gilt:
Fallunterscheidung
Fall 1:
Fall 2:
Fall 1:
liefert lokales Maximum mit
Setze in die Nebenbedingung ein, um zu bekommen. Setze beide Werte in ein , um die maximale Fläche zu berechnen.
Das maximale Rechteck ist demnach ein Quadrat mit der Seitenlänge .
Für die Fläche gilt:
Fall 2:
Damit liegt der Scheitelpunkt der Parabel rechts vom Intervall und nimmt in diesem Intervall streng monoton zu.
Die größte Fläche wird demnach - als Randextremum - angenommen, wenn der erzeugende Punkt mit dem rechten Randpunkt zusammenfällt. Also für .
Damit gilt für die Seitenlängen des gesuchten maximalen Rechtecks und .
Die maximale Fläche ist:
Die beiden folgenden Grafiken veranschaulichen die alternative Lösung der Aufgabe.
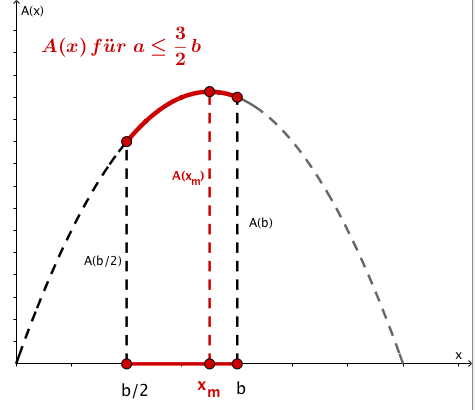
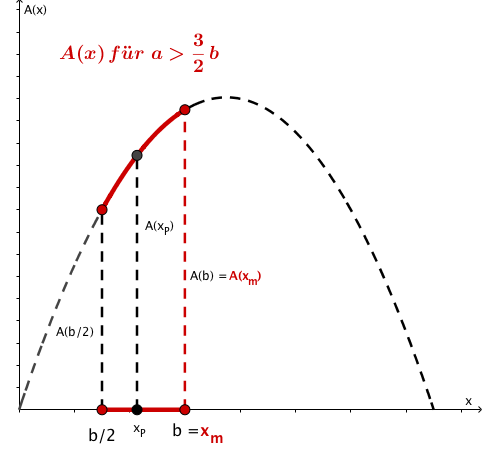
- 7
Aus einem kreisrunden Papierstück mit dem Radius R soll eine kegelförmige Popkorntüte hergestellt werden.
Wie muss das Papier zugeschnitten und zusammengeklebt werden, wenn die fertige Tüte mit möglichst viel Popcorn gefüllt werden soll?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Aus dem Kreis mit dem Radius wird ein Kreissektor mit dem Mittelpunktswinkel ausgeschnitten. Der ausgeschnittene Kreissektor ergibt den Mantel des Kegels.
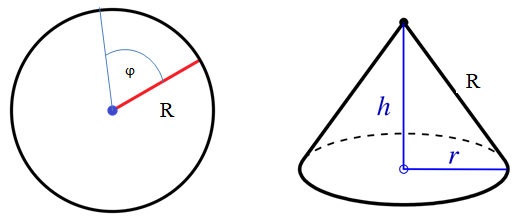
Aufstellen der Zielfunktion und der Nebenbedingung
Die Zielfunktion bei dieser Aufgabe ist das Volumen eines Kegels:
Die Nebenbedingung ergibt sich aus der obigen rechten Abbildung.
Im rechtwinkligen Dreieck gilt der Satz des Pythagoras:
Die Volumenfunktion hängt sowohl von als auch von ab, d.h. .
Um die Nebenbedingung in die Zielfunktion einzusetzen kann man sie nach einer der beiden Variablen oder auflösen. Man hat somit zwei Lösungsvarianten.
Die einfachere dieser beiden Lösungsvarianten ergibt sich, wenn das Volumen des Kegels nur von der Kegelhöhe abhängig ist, d.h. es muss bestimmt werden.
Lösungsvariante 1
Einsetzen in die Zielfunktion
Gleichung wird nach bzw. gleich nach aufgelöst: .
Dieses wird nun in die Zielfunktion eingesetzt um die Extremalfunktion als Funktion von zu erhalten:
.
Für den Definitionsbereich gilt: .
Bestimmung des Extremwertes
Leite die Extremalfunktion zweimal ab, um den Extremwert und die Art des Extremwertes bestimmen zu können.
Setze die erste Ableitung gleich Null:
Nach aufgelöst erhält man: .
Da ist, gilt: .
Setze Gleichung in die zweite Ableitung ein:
Da die zweite Ableitung kleiner Null ist, ist der Extremwert ein Maximum.
Bestimmung des Kegelgrundkreisradius
Setzt man in ein,
so erhält man:
Zieht man nun die Wurzel aus , so erhält man für den Radius des Grundkreises des Kegels:
Bestimmung des Mittelpunktwinkels
Für die Bogenlänge des ausgeschnittenen Kreissektors gilt:
Die Bogenlänge ist der Umfang des Kegelgrundkreises mit dem Radius .
nach aufgelöst:
.
Setzt man Gleichung in Gleichung ein,
erhält man
Anmerkung: Der Winkel ist von unabhängig.
Das maximale Volumen in Abhängigkeit von
Setzt man die Gleichungen und in Gleichung ein, so erhält man das maximale Volumen:
Beantwortung der Ausgangsfrage
Die Popkorntüte hat ein maximales Volumen, wenn aus dem Kreis mit Radius ein Kreissektor mit dem Mittelpunktswinkel ausgeschnitten wird.
Der Radius des Kegelgrundkreises beträgt .
Die Höhe des Kegels beträgt und sein maximales Volumen ist
.
Lösungsvariante 2
Einsetzen in die Zielfunktion
Löst man Gleichung nach auf, erhält man:
Setzt man Gleichung in Gleichung ein, erhält man das Volumen in Abhängigkeit von :
Für den Definitionsbereich gilt: .
Anmerkung: Für und ist das Volumen gleich Null.
Bestimmung des Extremwertes
Leite die Extremalfunktion zweimal ab, um den Extremwert und die Art des Extremwertes bestimmen zu können. Für diese Ableitung benötigst du die Produktregel, die Ableitung einer Wurzel und die Kettenregel. Der Rechenaufwand für diese Ableitung ist relativ hoch. Mit einem Rechentrick kann man den Rechenaufwand verringern. Der Funktionsterm wird so umgeformt, dass der Term unter die Wurzel gezogen wird. Man erhält Gleichung .
Für die Ableitung von Gleichung genügt die Betrachtung des Radikanden.
Nimmt der Radikand einen maximalen Wert an, so ist auch die Wurzel aus diesem maximalen Radikanden ebenfalls maximal. Damit ist auch maximal.
Wir betrachten nun den Radikanden als Funktion von .
und suchen das Maximum dieser Funktion.
Setze die erste Ableitung gleich Null:
Die Gleichung hat die Lösungen (entfällt hier, da ) und die Lösung
Da ist, gilt .
Zur Überprüfung, ob es sich um ein Maximum handelt, setze Gleichung in die zweite Ableitung ein:
Da die zweite Ableitung kleiner Null ist, ist der Extremwert ein Maximum.
Bestimmung der Höhe des Kegels
In Gleichung wird die Gleichung eingesetzt:
Bestimmung des Mittelpunktswinkels
In Gleichung wird die Gleichung eingesetzt .
Anmerkung: der Winkel ist von unabhängig.
Das maximale Volumen in Abhängigkeit von
Setzt man die Gleichung in Gleichung ein, so erhält man das maximale Volumen in Abhängigkeit von : .
Beantwortung der Ausgangsfrage
Die Popkorntüte hat ein maximales Volumen, wenn aus dem Kreis mit Radius ein Kreissektor mit dem Mittelpunktswinkel ausgeschnitten wird.
Der Radius des Kegelgrundkreises ist .
Die Höhe des Kegels beträgt und sein maximales Volumen ist
.
Beispiel
Für einen Kreisradius von ergibt sich ein Kegelgrundkreisradius von
, eine Kegelhöhe von und ein Mittelpunktswinkel
von .
Das maximale Volumen in diesem Beispiel beträgt
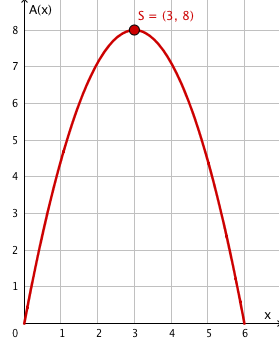
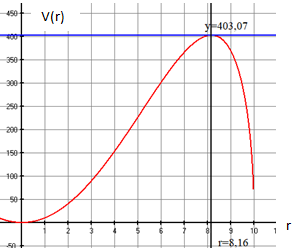
In der Abbildung ist die Extremalfunktion
für dargestellt.
Das Extremum befindet sich im Punkt
.
Mit den Maßen und
wurde ein Kegel hergestellt.
Unter dem Kegel befindet sich ein Lineal
zur Bestimmung des Durchmessers.

In diesem Bild ist die rechte Seite des Lineals zu sehen.
Es zeigt einen Durchmesser von
an. Der Radius beträgt
in guter Übereinstimmung mit dem berechneten Wert.

Bestimme die Zielfunktion und die Nebenbedingung. Ermittle daraus die Extremalfunktion und bestimme mit Hilfe der Ableitung den Extremwert.