Analysis, Teil A, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion $g : x \mapsto \sqrt{x + 1} - 2$ mit maximaler Definitionsmenge $D$ .
a)
(1 BE)
Geben Sie $D$ an.
b)
(4 BE)
Bestimmen Sie die Gleichung der Tangente an den Graphen von $g$ im Punkt $(8 | g (8))$ .

Die maximale Definitionsmenge und die Gleichung der Tangente einer Funktion in einem vorgegebenen Punkt sind zu bestimmen.
Lösung Teilaufgabe a)
Für die Bestimmung des maximalen Definitionsbereichs $D_{g}$ der Wurzelfunktion
$g : x \mapsto \sqrt{x + 1} - 2$
gilt die Bedingung, dass der Term $x + 1$ unter der Wurzel (der "Radikand") nicht negativ wird.
"nicht negativ" ist gleichwertig mit "größer oder gleich Null".
Löse also folgende Ungleichung:
$\begin{array}{rcll} x + 1 & \geq & 0 & | - 1 \\ x & \geq & - 1 \end{array}$
Der maximale Definitionsbereich $D_{g}$ kann somit folgendermaßen angegeben werden:
$D_{g} = {x | x \geq - 1}$ oder so: $D_{g} = [- 1; + \infty [$
Lösung Teilaufgabe b)
Bestimme die 2. Koordinate des Punktes $(8 | g (8))$ :
$g (8) = \sqrt{8 + 1} - 2 = 1$ .
Die Gleichung der Tangente soll also im Punkt $P (8 | 1)$ aufgestellt werden.
Bilde die 1.Ableitung $g^{'}$ von $g$ :
$\begin{array}{rcll} g (x) & = & (x + 1)^{\frac{1}{2}} - 2 & | Benutze die Potenz- und die Kettenregel \\ g^{'} (x) & = & \frac{1}{2} (x + 1)^{- \frac{1}{2}} \cdot 1 - 0 \\ = & \frac{1}{2} \cdot \frac{1}{(x + 1)^{\frac{1}{2}}} \\ g^{'} (x) & = & \frac{1}{2 \sqrt{x + 1}} \end{array}$
Im Punkt $P (8 | 1)$ hat die gesuchte Tangente die Steigung
$g^{'} (8) = \frac{1}{2 \sqrt{8 + 1}} = \frac{1}{6}$
Ein Ansatz für die Gleichung der Tangente lautet dann:
$t : y = \frac{1}{6} x + m$
Setze den Punkt $(8 | 1)$ ein, um $m$ zu berechnen:
$1 = \frac{8}{6} + m \Rightarrow m = - \frac{1}{3}$ .
Damit lautet die gesuchte Tangente:
$t : y = \frac{1}{6} x - \frac{1}{3}$
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die in $R ∖ {0}$ definierte Funktion $f : x \mapsto 1 - \frac{1}{x^{2}}$ , die die Nullstellen $x_{1} = - 1$ und $x_{2} = 1$ hat.
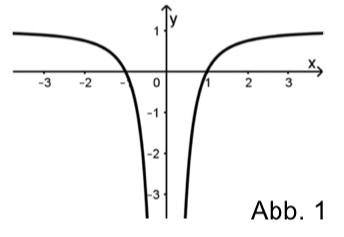
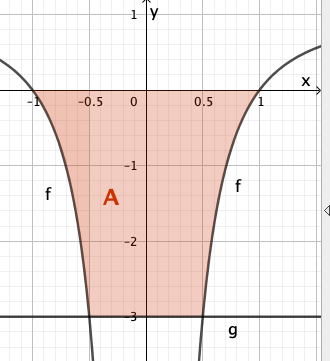
Abbildung 1 zeigt den Graphen von $f$ , der symmetrisch bezüglich der y-Achse ist.
Weiterhin ist die Gerade $g$ mit der Gleichung $y = - 3$ gegeben.
a)
(1 BE)
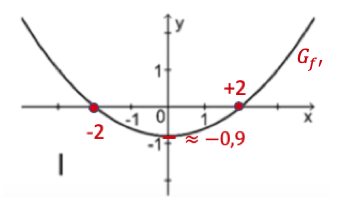
Zeigen Sie, dass einer der Punkte, in denen $g$ den Graphen von $f$ schneidet, die x-Koordinate $\frac{1}{2}$ hat.
b)
(4 BE)
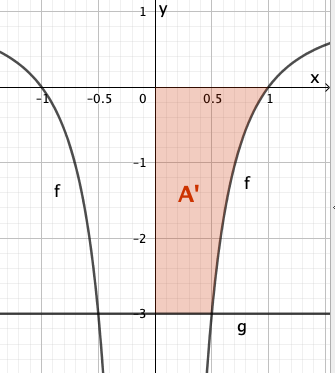
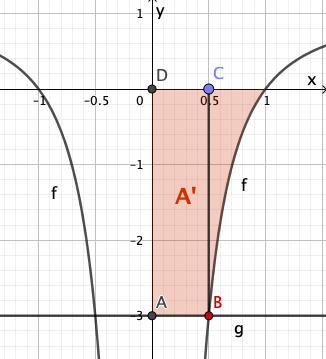
Bestimmen Sie rechnerisch den Inhalt der Fläche, die der Graph von $f$ , die x-Achse und die Gerade $g$ einschließen.

Im Zusammenhang mit einer gegebenen gebrochen-rationalen Funktion ist ein Flächenstück zu berechnen.
Lösung Teilaufgabe a)
In dieser Teilaufgabe sind die beiden Funktionen
$f : x \mapsto 1 - \frac{1}{x^{2}}$ und
$g : x \mapsto - 3$
zu schneiden.
Setze die beiden Funktionsterme gleich und löse die Gleichung.
$\begin{array}{rcll} 1 - \frac{1}{x^{2}} & = & - 3 & | \cdot x^{2} \\ x^{2} - 1 & = & - 3 x^{2} & | + 3 x^{2} + 1 \\ 4 x^{2} & = & 1 & | : 4 \\ x^{2} & = & \frac{1}{4} & | \sqrt{} \\ x_{1} & = & + \frac{1}{2} \\ x_{2} & = & - \frac{1}{2} \end{array}$
Einer der beiden Schnittpunkte der Graphen von $f$ und $g$ ist der Punkt $S (0,5 | - 3)$ .
Lösung Teilaufgabe b)
Die Teilaufgabe verlangt eine Flächenberechnung.
Schraffiere zunächst die zu berechnende Fläche in einer Skizze.
Achtung:
Gemeint ist eine Fläche, deren Rand allein aus Teilen des Graphen von $f$ , aus Teilen der x-Achse und Teilen des Graphen von $g$ besteht.
Die richtige Fläche
Eine falsche Fläche
Die Fläche $A^{'}$ ist deshalb nicht die richtige Fläche, da ihr Rand einen Teil der y-Achse enthält.
Dennoch ist $A^{'}$ hilfreich zur Berechnung der Fläche $A$ , da - wegen der Symmetrie des Graphen von $f$ zur y-Achse - gilt: $A = 2 \cdot A^{'}$ .
So berechnest du die Fläche $A^{'}$ :
$\begin{array}{rcll} A^{'} & = & {Rechteck}_{A B C D} + | \int_{0,5}^{1} f (x) dx | \\ = & 0,5 \cdot 3 + | \int_{0,5}^{1} (1 - \frac{1}{x^{2}}) dx | \end{array}$
$\begin{array}{rcll} A^{'} & = & 1,5 + | [x + x^{- 1}]_{0,5}^{1} | \\ = & 1,5 + | (1 + 1) - (0,5 + 2) | \\ = & 1,5 + 0,5 \\ A^{'} & = & 2 \end{array}$
Damit gilt für die gesuchte Fläche der Teilaufgabe:
$A = 4$
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
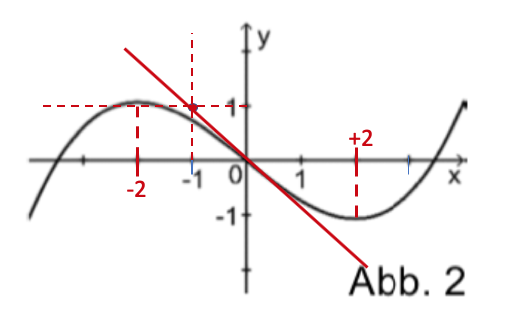
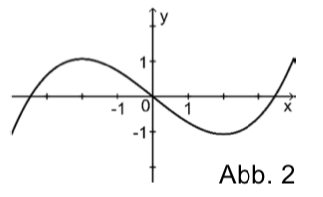
Die nebenstehende Abbildung 2 zeigt den Graphen einer Funktion $f$ .
a)
(3 BE)
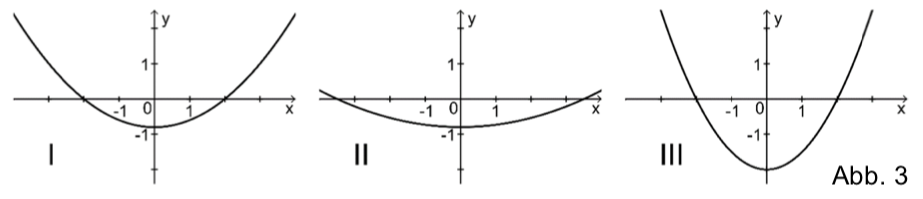
Einer der folgenden Graphen I, II, und III gehört zur ersten Ableitungsfunktion von $f$ . Geben Sie diesen Graphen an. Begründen Sie, dass die beiden anderen Graphen dafür nicht infrage kommen.
b)
(2 BE)
Die Funktion $F$ ist eine Stammfunktion von $f$ . Geben Sie das Monotonieverhalten von $F$ im Intervall $[1; 3]$ an. Begründen Sie Ihre Angabe.

Aus gegebenen Graphen sind charakteristische Eigenschaften der zugehörigen Funktionen zu erschließen bzw. im Rahmen der Zeichengenauigkeit vernünftig abzuschätzen.
Lösung Teilaufgabe a)
Infrage kommt nur der Graph I.
Begründung:
Der Graph der Funktion $f$ hat für die (geschätzten) Werte $x_{1} = - 2$ und $x_{2} = + 2$ lokale Extrema.
Die Ableitungsfunktion $f^{'}$ der Funktion $f$ muss deshalb (etwa) für diese Werte Nullstellen haben.
Damit scheidet Graph II aus.
Dem Graphen von $f$ entnimmt man für $x = 0$ eine (Wende-)Tangente mit einer geschätzten Steigung von etwa $- 1$ .
Damit scheidet der Graph III aus. Denn für diesen Graph gilt $f^{'} (0) \approx - 2$ . Der Graph I dagegen passt mit $\approx - 0,9$ gut.
Lösung Teilaufgabe b)
Die Lösung der Aufgabe verlangt die Vertrautheit mit dem Zusammenhang einer Funktion und einer ihrer Stammfunktionen und Kenntnis eines Monotoniekriteriums.
Ergebnis:
Jede Stammfunkktion $F$ ist im Intervall $[1; 3]$ monoton fallend.
Begründung:
Für jede Stammfunktion $F$ ist $f$ die zugehörige Ableitungsfunktion.
Da $f$ im Intervall $[1; 3]$ negativ ist, ist nach dem Monotoniekriterium differenzierbarer Funktionen $F$ monoton fallend.
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Schar der in $ℝ$ definierten Funktionen $p_{k} : x \mapsto k x^{2} - 4 x - 3$ mit $k \in R ∖ {0}$ , deren Graphen Parabeln sind.
Bestimmen Sie den Wert von $k$ so, dass der Punkt $(2 | - 3)$ auf der zugehörigen Parabel liegt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionenschar
In der Aufgabe sind Lagebeziehungen bei einer Funktionenschar zu untersuchen.
Gegeben ist die Funktionenschar
$p_{k} : x \mapsto k x^{2} - 4 x - 3$
und der Punkt $P (2 | - 3)$ .
Setze die Koordinaten von $P$ in die Funktionsgleichung der Schar ein und löse nach $k$ auf.
$- 3$ $=$ $k \cdot 22 - 4 \cdot 2 - 3$
$- 3$ $=$ $4 k - 11$ $+ 11$
$4 k$ $=$ $8$ $: 4$
$k$ $=$ $2$
Der Punkt $P (2 ∣ - 3)$ liegt auf der Parabel $p_{k}$ :
$p_{2} : x \mapsto 2 x^{2} - 4 x - 3$

Ermitteln Sie diejenigen Werte von $k$ , für die die jeweils zugehörige Funktion $p_{k}$ keine Nullstelle besitzt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionenschar
Dass eine Funktion der Schar keine Nullstelle hat, bedeutet, dass die Gleichung $p_{k} (x) = 0$ keine Lösung hat.
Somit darf die quadratische Gleichung
$k x^{2} - 4 x - 3 = 0$
keine Lösung haben.
Also muss deren Diskriminante negativ sein.
$16 + 12 k$ $<$ $0$ $- 16$
$12 k$ $<$ $- 16$ $: 12$
$k$ $<$ $- \frac{3}{4} $
Für alle Funktionen der Schar $p_{k}$ mit $k < - \frac{4}{3}$ haben die Graphen keine Nullstelle.