Aufgaben zum Thema Analysis

1
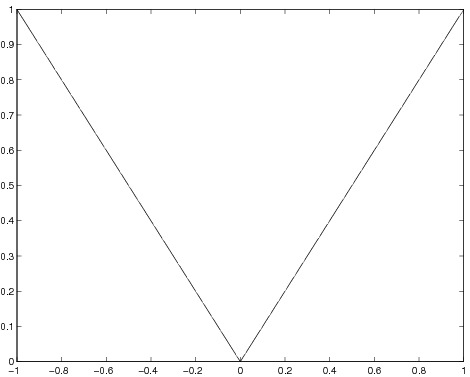
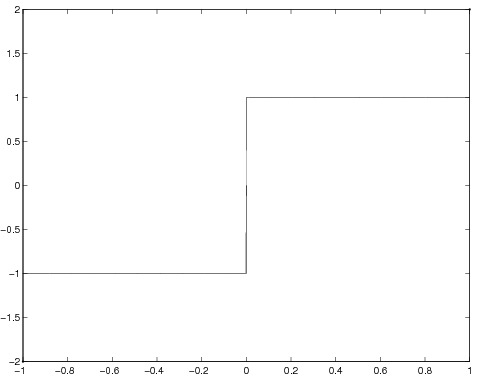
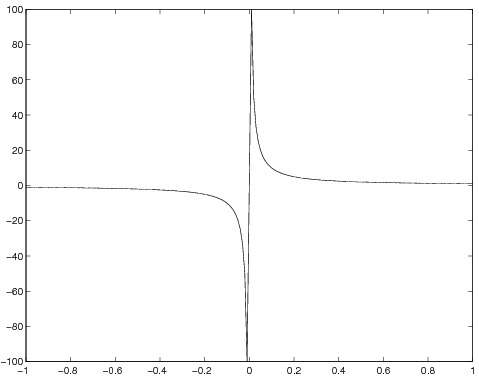
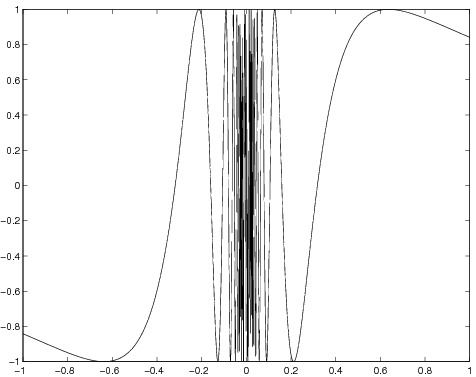
Entscheide, ob die folgenden Funktionen stetig sind (ohne Begründung).
$f (x) = abs (x) = | x |$

$f (x) = sign (x) = {\begin{matrix} 1, & für x > 0, \\ 0, & für x = 0, \\ - 1, & für x < 0. \end{matrix}$

$f (x) = \frac{1}{x}$

$f (x) = \sin (\frac{1}{x})$

$f (x) = x \sin (\frac{1}{x})$

$f (x) = {\begin{matrix} 1, & für x \in ℚ, \\ - 1, & für x \notin ℚ . \end{matrix}$
2
Zeige direkt anhand der $ϵ$ - $δ$ -Definition die Stetigkeit der Funktion $f (x) = | x |$ . Wie kannst du anhand der $ϵ$ - $δ$ -Definition zeigen, dass die Signumsfunktion
$sign (x) = {\begin{matrix} 1 & f \ddot{u} r x > 0, \\ 0 & f \ddot{u} r x = 0, \\ - 1 & f \ddot{u} r x < 0 \end{matrix}$ in $x = 0$ nicht stetig ist?
3
Leite mit Hilfe der Kettenregel die Ableitung von $\frac{1}{g (x)}$ und anschließend mit der Produktregel die Ableitung von $\frac{f (x)}{g (x)}$ her.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Analysis
Zur Erinnerung: Die Kettenregel lautet: $(h (g (x)))^{'} = h^{'} (g (x)) g^{'} (x)$ .
Wenn wir nun $\frac{1}{g (x)}$ ableiten wollen, dann können wir
$h (x) = \frac{1}{x} \Rightarrow h (g (x)) = \frac{1}{g (x)}$
wählen und die Kettenregel benutzen:
$(h (g (x)))^{'} = h^{'} (g (x)) g^{'} (x) = - \frac{1}{(g (x))^{2}} g^{'} (x) = - \frac{g^{'} (x)}{(g (x))^{2}} ■$
Nun kommen wir zum zweiten Teil der Aufgabe, dem Ableiten von
$\frac{f (x)}{g (x)} = f (x) \cdot \frac{1}{g (x)}$
Dazu wenden wir die Produktregel und die gerade ermittelte Ableitungsregel an:
${(f (x) \frac{1}{g (x)})}^{'} = f^{'} (x) \frac{1}{g (x)} + f (x) (- \frac{g^{'} (x)}{(g (x))^{2}})$
$= \frac{f^{'} (x) \cdot g (x)}{g (x) \cdot g (x)} - \frac{f (x) g^{'} (x)}{(g (x))^{2}} = \frac{f^{'} (x) g (x) - f (x) g^{'} (x)}{(g (x))^{2}}$
Und damit sind wir bei der Quotientenregel gelandet.
4
Der Mittelwertsatz der Differentialrechnung lautet:
Die Funktion $f$ sei im Intervall $[a, b]$ mit $a < b$ stetig und im Inneren $(a, b)$ differenzierbar.
Dann existiert ein $c \in [a, b]$ mit
$f (b) - f (a) = f^{'} (c) (b - a) .$
Was bedeutet dieser Satz anschaulich?

Beweise den Satz von Rolle:
Die Funktion $f$ sei im Intervall $[a, b]$ stetig differenzierbar und es gelte $f (a) = f (b)$ .Dann besitzt der Graph von $f$ zwischen $a$ und $b$ mindestens einen Punkt mit waagrechter Tangente.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Analysis
An einem Punkt $x$ , an dem $f$ eine waagrechte Tangente hat, gilt $f^{'} (x) = 0$ (da die waagrechte Tangente nicht steigt oder fällt).Wenn $f (a) = f (b)$ , dann ist natürlich $f (b) - f (a) = 0$ .Nun betrachten wir den Mittelwertsatz (wir haben ja vorausgesetzt, dass $f$ im Intervall $[a, b]$ stetig differenzierbar ist; zusätzlich muss $a \neq b$ gelten, denn sonst wäre, sobald der Satz bewiesen ist, in jedem Punkt eine waagrechte Tangente):
$f (b) - f (a) = f^{'} (c) (b - a)$
Mit der oben erkannten Eigenschaft ergibt sich:
$0 = f^{'} (c) (b - a)$
Da wir $a \neq b$ noch zusätzlich vorausgesetzt haben, können wir durch $(b - a)$ dividieren:
$0 = f^{'} (c)$
Und damit haben wir am Punkt $ξ \in [a, b]$ eine waagrechte Tangente. Da nach mindestens einer solcher verlangt war, haben wir den Satz von Rolle bewiesen.
$■$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org