Heft 2 - B1

🎓 Prüfungsbereich für Schleswig-Holstein

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Hier findest du die Aufgaben und Lösungen des Mathe MSA 2023 Prüfungsteil 2 Aufgabe 1.

Link zur Formelsammlung

Ein Taschenrechner ist in diesem Prüfungsteil erlaubt.

1
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
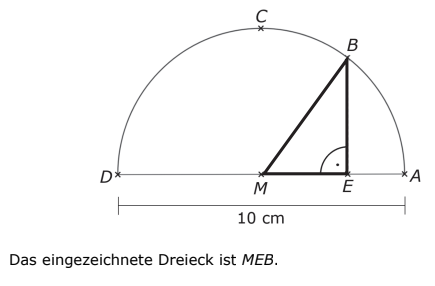
André untersucht mithilfe einer Geometriesoftware Punkte auf einem Halbkreis mit dem Radius $5 c m$ um den Mittelpunkt $M$ . Die Punkte $A, B$ und $C$ lassen sich auf der Kreislinie verschieben.
André untersucht die Abstände der Punkte $A, B$ und $C$ zueinander.
Berechne den Abstand der Punkte $C$ und $B$ in Zentimetern für $α = 75^{\circ}$ . (3 Punkte)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
Kosinussatz: $c^{2} = a^{2} + b^{2} - 2 a b \cdot \cos (γ)$
$a = b = 5 cm$
$γ = 90 ° - α = 90 ° - 75 ° = 15 °$
Einsetzen:
${B C}^{2} = 5^{2} + 5^{2} - 2 \cdot 5 \cdot 5 \cdot \cos (15 °)$
${B C}^{2} = 50 - 50 \cdot \cos (15 °) = 50 - 50 \cdot 0,9659 = 1,705$
$B C \approx 1,3$
Verwende die Formel des Kosinussatzes für das allgemeine Dreieck.

Der Abstand $a$ der Punkte $A$ und $C$ zueinander ist $a = \sqrt{2} \cdot 5 c m$ .
Zeige, dass das stimmt. (2 Punkte)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
Kosinussatz: $c^{2} = a^{2} + b^{2} - 2 a b \cdot \cos (α)$
$a = b = 5 cm$
$α = 90 °$
Einsetzen:
$| A C |^{2} = 5^{2} + 5^{2} - 2 \cdot 5 \cdot 5 \cdot \cos (90 °)$
$| A C |^{2} = 50 - 50 \cdot \cos (90 °) = 50$
$| A C | = \sqrt{50} = \sqrt{2 \cdot 25} = \sqrt{2} \cdot 5$
Der Abstand $a$ beträgt $\sqrt{2} \cdot 5 cm$ .
Alternative:
Das Dreieck $A C M$ ist bei $M$ rechtwinklig.
Daher gilt mit dem Satz des Pythagoras
$| A C |^{2} = | A M |^{2} + | C M |^{2} = 5^{2} + 5^{2} = 50$
$| A C | = \sqrt{50} = 2 \sqrt{5}$
Verwende den Kosinussatz für das allgemeine Dreieck.

André verschiebt den Punkt $B$ so, dass $A$ und $B$ den Abstand $5 c m$ voneinander haben.
Gib die Größe des Winkels $α$ an. (1 Punkt)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
Kosinussatz: $c^{2} = a^{2} + b^{2} - 2 a b \cdot \cos (α)$
$| A B | = c = 5 cm$
$a = b = 5 cm$
Einsetzen:
$5^{2} = 50 - 50 \cdot \cos (α)$
$0,5 = \cos (α)$
$α = 60 °$
Die Größe des Winkels $α$ beträgt 60°.
Alternative:
Das Dreieck $A B M$ ist gleichseitig, da alle Seitenlängen $5 cm$ betragen. Daher sind alle Innenwinkel $60^{\circ}$ .
Verwende den Kosinussatz für das allgemeine Dreieck.
2
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
André verschiebt den Punkt $B$ so, dass der Punkt $E$ den Durchmesser des Halbkreises im Verhältnis 8:2 teilt.
André nutzt den Höhensatz zur Berechnung des Abstands der Punkte $B$ und $E$ .
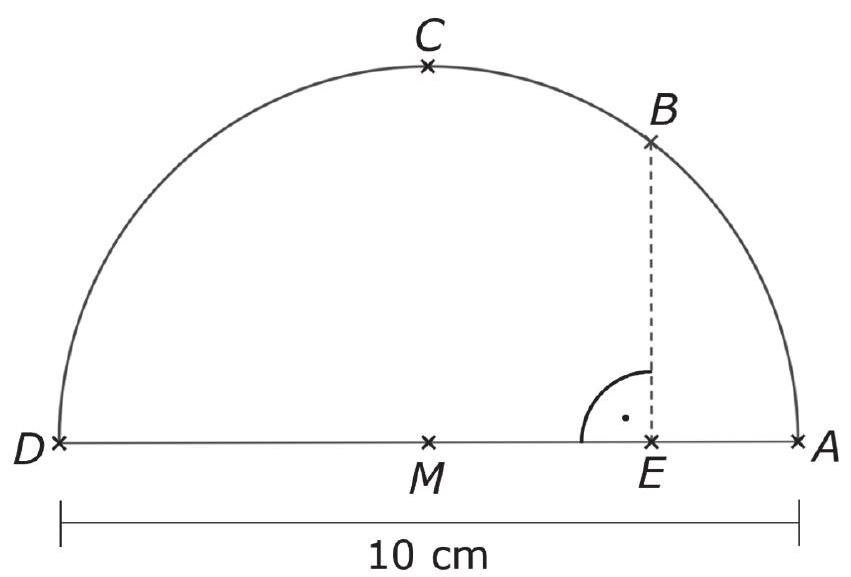
Berechne den Abstand der Punkte $B$ und $E$ mithilfe des Höhensatzes. (2 Punkte)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Höhen- und Kathetensatz
Höhenstatz: $h^{2} = p \cdot q$
$p = 2 cm, q = 8 cm$
$| B E | = \sqrt{p \cdot q}$
$| B E | = \sqrt{2 \cdot 8} = 4$
Der Abstand der Punkte $B$ und $E$ zueinander beträgt $4 cm$ .
Bestimme zuerst die Längen der Strecken $A E$ und $D E$ .
Verwende dann den Höhensatz mit diesen Längen.

Mila rechnet lieber mit dem Satz des Pythagoras.
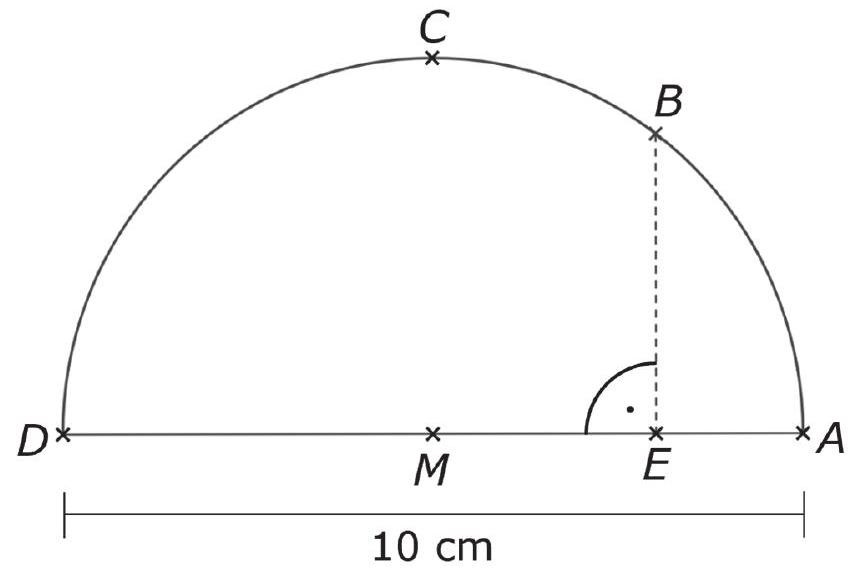
Zeichne das Dreieck ein, mit dem Mila den Abstand der Punkte $B$ und $E$ berechnen kann. (1 Punkt)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Pythagoras
Verbinde die Punkte M, B und E miteinander. Du erhälst ein rechtwinkliges Dreieck. Für die Berechnung des Abstands der Punkte $B$ und $E$ kannst du den Satz des Pythagoras verwenden:
Das Dreieck $M E B$ ist bei $M$ rechtwinklig.
Da $| D E | = 8 cm$ und $| D M | = 5 cm$ ist, ist $| M E | = 3 cm$ .
Der Radius $| M B |$ ist $5 cm$ .
Daher ist $| B E |^{2} = 5^{2} - 3^{2} = 25 - 9 = 16$
und $| B E | = 4 cm$ .
Verbinde die Punkte M, E und B miteinander zu einem rechtwinkligen Dreieck.
3
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
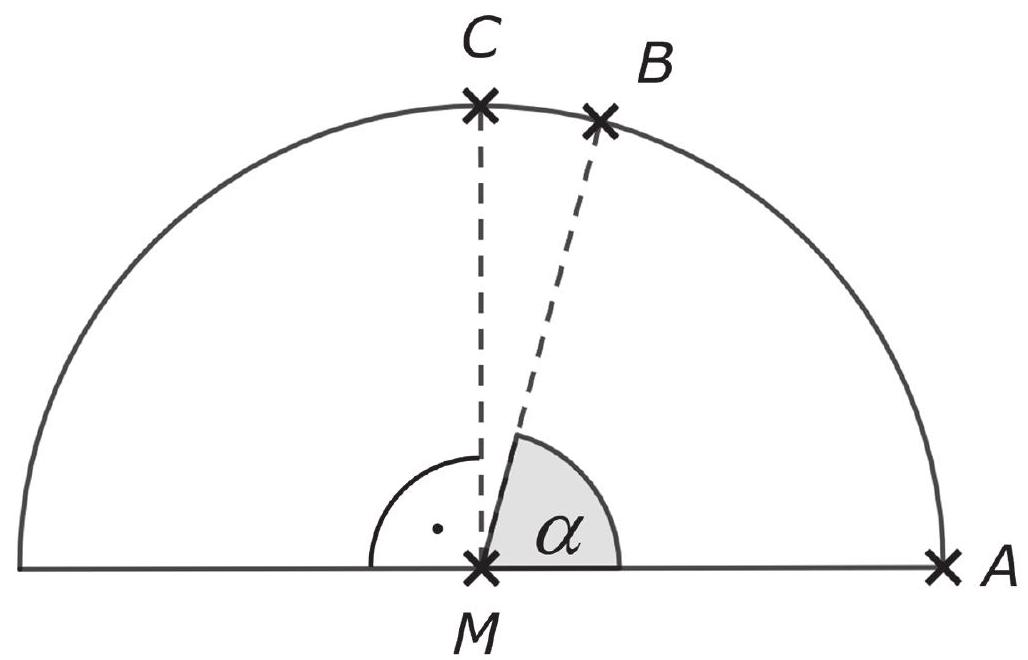
André will die Punkte so auf der Kreislinie verschieben, dass sowohl der Punkt $A$ als auch der Punkt $C$ vom Punkt $B$ den Abstand $5 c m$ hat.
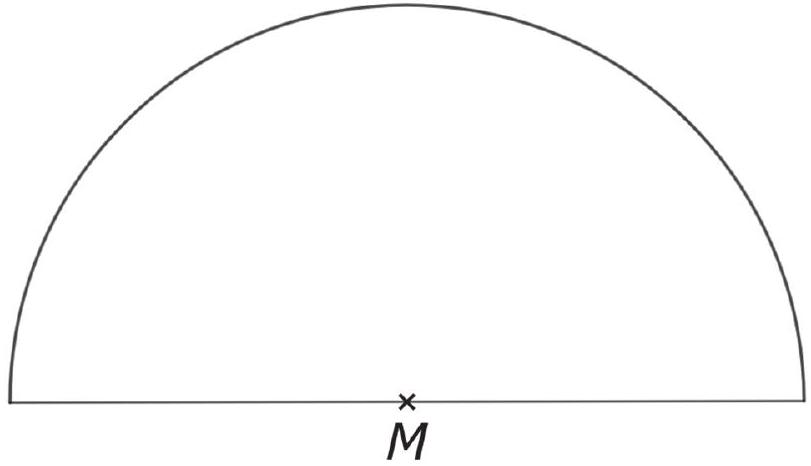
Zeichne den Sachverhalt in der Abbildung. (2 Punkte)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreise und Kreisteile
Einzeichnen der Punkte $A, B, C$ :
Die Punkte $A, B$ und $C$ liegen auf dem Halbkreis.
Für die Winkel $α$ und $β$ gilt: $α = β = 60 °$
Da der Kreis einen Durchmesser von $10 cm$ hat, entsprechen $5 cm$ gerade dem Radius. Verschiebe die Punkte so, dass sie einen Radius Abstand zueinander haben.
4
Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Ministerium für Allgemeine und Berufliche Bildung, Wissenschaft, Forschung und Kultur des Landes Schleswig-Holstein zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
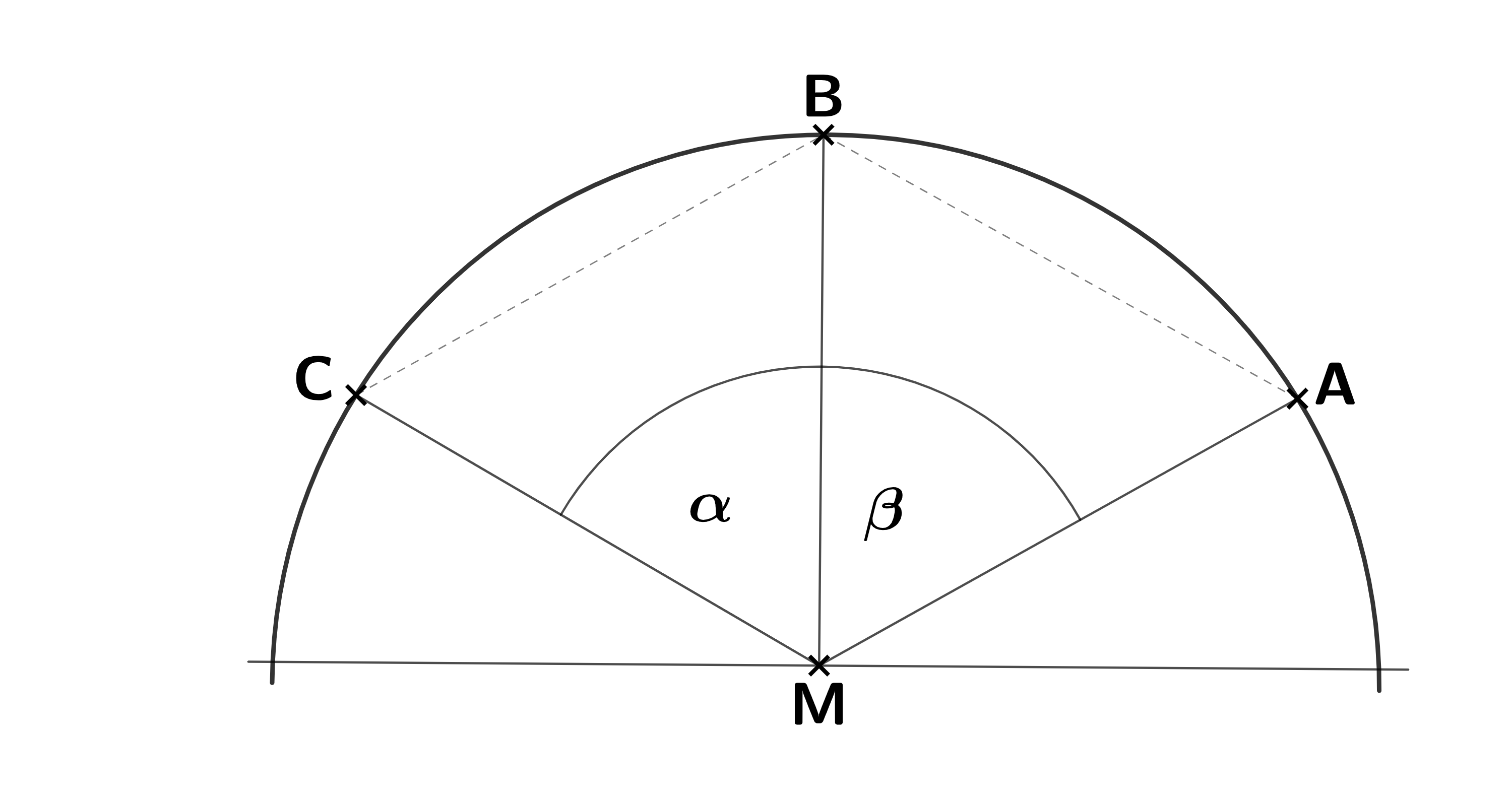
André untersucht, wie sich der Winkel $β$ ändert, wenn sich der Abstand zwischen den Punkten $B$ und $C$ verändert.
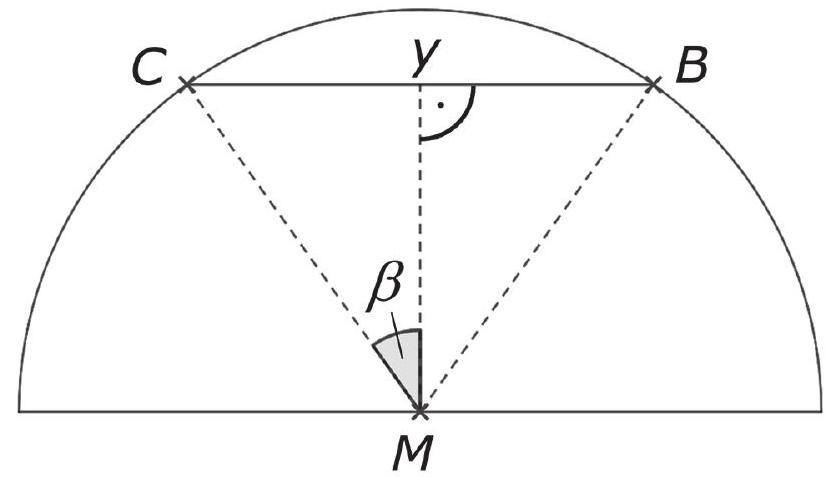
André sagt: "Zur Untersuchung kann ich die Gleichung $\sin (β) = \frac{0,5 y}{5}$ nutzen."
Entscheide und begründe, ob André recht hat. (3 Punkte)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens
André hat mit seiner Aussage recht.
Für seine Untersuchung verwendet er den Sinus:
$\sin (α) = \frac{Gegenkathete}{Hypotenuse}$
Die Hypotenuse hat die Länge $5 cm$ .
Die Gegenkathete hat die Länge $\frac{1}{2} \cdot y$
Durch Einsetzen der Werte untersucht André den Winkel $β$
$\sin (β) = \frac{0,5 y}{5}$

André erhält bei seiner Untersuchung das Ergebnis $\sin (β) = 1$ .
Stelle die Bedeutung dieses Wertes für die Punkte $B$ und $C$ dar. (1 Punkt)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens
Aus einer Wertetabelle kann André ablesen, dass bei einem Winkel von $β = 90^{\circ}$ der Sinuswert $\sin (90^{\circ}) = 1$ ist.
Das bedeutet, dass die Punkte $B$ und $C$ auf dem Kreisbogen so weit nach unten verschoben werden, dass sie sich genau gegenüberliegen.
Der Abstand der beiden Punkte voneinander entspricht dann dem Durchmesser des Kreises.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

Heft 2 - B1

Einzeichnen der Punkte A, B, C :

Einzeichnen der Punkte $A, B, C$ :