Aufgaben zu Winkeln zwischen Vektoren
Mit diesen gemischten Aufgaben lernst du, den Winkel zwischen Vektoren zu bestimmen. Schaffst du sie alle?
- 1
Bestimme den Winkel, den die beiden Vektoren einschließen.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Du hast zwei Vektoren gegeben, deren gemeinsamen Winkel du berechnen sollst. Dies geht mit der Formel
In unserem Fall haben wir die beiden Vektoren und .
Diese setzst du ein und erhätst:
Löse die Formel nach um:
Schließlich bestimmst du das Skalarprodukt für den Zähler sowie die beiden Längen für den Nenner.
Aus der Division der beiden Ergebisse bekommst du nun den Faktor, den du in den Arkuskosinus einsetzt.
Also beträgt der Schnittwinkel .
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren berechnen
Du hast zwei Vektoren gegeben, deren gemeinsamen Winkel du berechnen sollst. Dies geht mit der Formel
In unserem Fall hast du die beiden Vektoren und . Diese setzst du ein und erhältst:
Löse die Formel nach auf:
Schließlich bestimmst du das Skalarprodukt für den Zähler sowie die beiden Längen für den Nenner.
Aus der Division der beiden Ergebisse bekommst du nun den Faktor, den du in den Arkuskosinus einsetzt.
Schließlich kommst du auf den gesuchten Winkel.
Also beträgt der Schnittwinkel .
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
In dieser Aufgabe geht es darum, den Winkel zw. zwei Vektoren zu berechnen.
Du hast zwei Vektoren und gegeben, deren gemeinsamen Winkel du berechnen sollst. Dies geht mit der Formel
Danach bildest du den Arkuskosinus und kommst auf:
Anschaulich bedeutet das, dass die beiden Vektoren genau entgegengesetzt gerichtet sind bzw. dass sich als schreiben lässt, wobei eine reelle Zahl.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
In dieser Aufgabe geht es darum, den Winkel zw. zwei Vektoren zu berechnen.
Du hast zwei Vektoren und gegeben, deren gemeinsamen Winkel du berechnen sollst. Dies geht mit der Formel
Danach bildest du den Arkuskosinus und kommst auf:
also beträgt der Winkel .
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Die Berechnung des Winkels zwischen zwei Vektoren verwendet die Länge der jeweiligen Vektoren und das Skalarprodukt zwischen den beiden. Ein Spezialfall liegt vor, wenn das Skalarprodukt ist. Das ist genau dann der Fall, wenn die beiden Vektoren senkrecht aufeinander stehen.
Berechne das Skalarprodukt zwischen und !
Das Skalarprodukt von und ist also . Daher stehen die beiden Vektoren senkrecht aufeinander und der eingeschlossene Winkel beträgt also .
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Um den eingeschlossenen Winkel zwischen den Vektoren zu berechnen, benötigst du die Länge der beiden Vektoren und das Skalarprodukt von und . Berechne nun zunächst diese Größen!
Länge der Vektoren berechnen
Zur Berechnung der Länge eines Vektors bildest du das Skalarprodukt des Vektors mit sich selbst und ziehst dann die Wurzel daraus.
Du berechnest zunächst das Skalarprodukt von mit sich selbst und mit sich selbst:
Indem du jetzt jeweils die Wurzel aus dem Skalarprodukt ziehst, erhältst du die Längen der Vektoren:
und
Skalarprodukt berechnen
Jetzt musst du das Skalarprodukt der beiden Vektoren berechnen.
Das Skalarprodukt wird allgemein gebildet durch .
Hier also:
Das Skalarprodukt von und ist somit .
Winkel berechnen
Mit den bisher berchneten Größen kannst du jetzt den gesuchten Winkel berechnen. Dafür benutzt du die Formel zur Winkelberechnung:
Setze jetzt die bereits berechneten Größen ein!
Der Winkel zwischen den beiden Vektoren beträgt .
- 2
Prüfe, ob die beiden Vektoren senkrecht aufeinander stehen.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
Zwei Vektoren stehen senkrecht aufeinander, wenn ihr Skalarprodukt ergibt.
Das Skalarprodukt von und ist . Die beiden Vektoren stehen also senkrecht aufeinander.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
Zwei Vektoren stehen senkrecht aufeinander, wenn ihr Skalarprodukt ergibt.
Das Skalarprodukt von und ist .Die beiden Vektoren stehen also nicht senkrecht aufeinander.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
Zwei Vektoren stehen senkrecht aufeinander, wenn ihr Skalarprodukt ergibt.
=
Das Skalarprodukt von und ist .Die beiden Vektoren stehen also senkrecht aufeinander.
und
Orthogonalität von Vektoren
Zwei Vektoren stehen senkrecht aufeinander, wenn ihr Skalarprodukt ergibt.
Falls du einen Taschenrechner benutzt, ist die Rechnung natürlich kein Problem. Mit einer kleinen Nebenrechnung kommst du aber auch ohne Nebenrechnung weiter.
Nebenrechnung:
Damit ergibt sich insgesamt:
Das Skalarprodukt von und ist . Die beiden Vektoren stehen also senkrecht aufeinander.
- 3
Bestimme einen Vektor so, dass er orthogonal zu dem gegebenen Vektor und nicht der Nullvektor ist.
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
In dieser Aufgabe möchtest du zu einem gegebenen Vektor einen orthogonalen Vektor finden. Also suchst du einen Vektor , sodass das Skalarprodukt zwischen und Null ist.
Es lässt sich (zur Vereinfachung) annehmen. Dann erhältst du die Gleichung:
Durch Umformen siehst du, dass gelten muss:
Eine geeignete Wahl ist z.B gegeben durch und . Du erhältst also:
Du kannst jetzt die Probe machen, um nachzurechnen, dass die Vektoren tatsächlich senkrecht aufeinander stehen:
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
In dieser Aufgabe möchtest du zu einem gegebenen Vektor einen orthogonalen Vektor finden. Also suchst du einen Vektor , sodass das Skalarprodukt zwischen und ist.
Es lässt sich annehmen. Dann erhältst du die Gleichung:
Durch Umformen siehst du, dass gelten muss:
Eine geeignete Wahl ist z.B gegeben durch und . Du erhältst also:
Du kannst jetzt die Probe machen, um nachzurechnen, dass die Vektoren tatsächlich senkrecht aufeinander stehen:
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
In dieser Aufgabe möchtest du zu einem gegebenen Vektor einen orthogonalen Vektor finden. Also suchst du einen Vektor , sodass das Skalarprodukt zwischen und ist.
Es lässt sich annehmen. Dann erhältst du die Gleichung:
Durch Umformen siehst du, dass gelten muss:
Eine geeignete Wahl ist z.B gegeben durch und . Du erhältst also:
Du kannst jetzt die Probe machen, um nachzurechnen, dass die Vektoren tatsächlich senkrecht aufeinander stehen:
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
In dieser Aufgabe möchtest du zu einem gegebenen Vektor einen orthogonalen Vektor finden. Also suchst du einen Vektor , sodass das Skalarprodukt zwischen und ist.
Es lässt sich annehmen. Dann erhältst du die Gleichung:
Durch Umformen siehst du, dass gelten muss:
Eine geeignete Wahl ist z.B gegeben durch und . Du erhältst also:
Du kannst jetzt die Probe machen, um nachzurechnen, dass die Vektoren tatsächlich senkrecht aufeinander stehen:
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
In dieser Aufgabe möchtest du zu einem gegebenen Vektor einen orthogonalen Vektor finden. Also suchst du einen Vektor , sodass das Skalarprodukt zwischen und ist.
Es lässt sich annehmen, wegen . Dann erhältst du die Gleichung:
Durch Umformen siehst du, dass gelten muss:
Eine geeignete Wahl ist z.B gegeben durch und . Du erhältst also:
Du kannst jetzt die Probe machen, um nachzurechnen, dass die Vektoren tatsächlich senkrecht aufeinander stehen:
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
In dieser Aufgabe möchtest du zu einem gegebenen Vektor einen orthogonalen Vektor finden. Also suchst du einen Vektor , sodass das Skalarprodukt zwischen und ist.
Es lässt sich annehmen, wegen . Dann erhältst du die Gleichung:
Durch Umformen siehst du, dass gelten muss:
Eine geeignete Wahl ist z.B gegeben durch und . Du erhältst also:
Du kannst jetzt die Probe machen, um nachzurechnen, dass die Vektoren tatsächlich senkrecht aufeinander stehen:
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
In dieser Aufgabe möchtest du zu einem gegebenen Vektor einen orthogonalen Vektor finden. Also suchst du einen Vektor , sodass das Skalarprodukt zwischen und ist.
Es lässt sich annehmen. Dann erhältst du die Gleichung:
Durch Umformen siehst du, dass gelten muss:
Eine geeignete Wahl ist z.B gegeben durch und . Du erhältst also:
Du kannst jetzt die Probe machen, um nachzurechnen, dass die Vektoren tatsächlich senkrecht aufeinander stehen:
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
In dieser Aufgabe möchtest du zu einem gegebenen Vektor einen orthogonalen Vektor finden. Also suchst du einen Vektor , sodass das Skalarprodukt zwischen und ist.
Es lässt sich annehmen. Dann erhältst du die Gleichung:
Durch Umformen siehst du, dass gelten muss:
Eine geeignete Wahl ist z.B gegeben durch und . Du erhältst also:
Du kannst jetzt die Probe machen, um nachzurechnen, dass die Vektoren tatsächlich senkrecht aufeinander stehen:
Für diese Aufgabe benötigst Du folgendes Grundwissen: orthogonale Vektoren
In dieser Aufgabe möchtest du zu einem gegebenen Vektor einen orthogonalen Vektor finden. Also suchst du einen Vektor , sodass das Skalarprodukt zwischen und ist.
Es lässt sich annehmen. Dann erhältst du die Gleichung:
Durch Umformen siehst du, dass gelten muss:
Eine geeignete Wahl ist z.B gegeben durch und . Du erhältst also:
Du kannst jetzt die Probe machen, um nachzurechnen, dass die Vektoren tatsächlich senkrecht aufeinander stehen:
- 4
Berechne den Winkel zwischen zwei Vektoren.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Benutze die Formel zum Berechnen des Winkels zwischen zwei Vektoren.
↓ Setz die Werte ein.
↓ Berechne das Skalarprodukt und die Beträge der Vektoren.
↓ Vereinfache.
↓ Verwende den Gegenkosinus, um den Winkel zu ermitteln.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Benutze die Formel zum Berechnen des Winkels φ zwischen zwei Vektoren.
↓ Setz die Werte ein.
↓ Berechne das Skalarprodukt und die Beträge der Vektoren.
↓ Vereinfache.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Benutze die Formel zum Berechnen des Winkels zwischen zwei Vektoren.
↓ Setz die Werte ein.
↓ Berechne das Skalarprodukt und die Beträge der Vektoren.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Benutze die Formel zum Berechnen des Winkels zwischen zwei Vektoren.
↓ Setz die Werte ein.
↓ Berechne das Skalarprodukt und die Beträge der Vektoren.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Benutze die Formel zum Berechnen des Winkels zwischen zwei Vektoren.
↓ Setz die Werte ein.
↓ Berechne das Skalarprodukt und die Beträge der Vektoren.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Benutze die Formel zum Berechnen des Winkels zwischen zwei Vektoren.
↓ Setz die Werte ein.
↓ Berechne das Skalarprodukt und die Beträge der Vektoren.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Benutze die Formel zum Berechnen des Winkels φ zwischen zwei Vektoren.
↓ Berechne das Skalarprodukt und die Beträge der Vektoren.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Benutze die Formel zum Berechnen des Winkels zwischen zwei Vektoren.
↓ Setz die Werte ein.
↓ Berechne das Skalarprodukt und die Beträge der Vektoren.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel zwischen zwei Vektoren
Benutze die Formel zum Berechnen des Winkels φ zwischen zwei Vektoren.
↓ Setz die Werte ein.
↓ Berechne das Skalarprodukt und die Beträge der Vektoren.
- 5
Gegeben ist ein Würfel mit der Kantenlänge .
Berechne für den abgebildeten Würfel den Winkel zwischen der Flächendiagonalen und der Raumdiagonalen .
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Der Punkt des Würfels hat die Koordinaten .
Der Punkt hat die Koordinaten und hat die Koordinaten .
Für den Vektor gilt:
Für den Betrag dieses Vektors folgt:
Für den Vektor gilt:
Für den Betrag dieses Vektors folgt:
Den Winkel berechnest du mit:
↓ Setze die berechneten Werte ein.
↓ Berechne das Skalarprodukt und fasse die Wurzeln zusammen.
↓ Vereinfache.
Den Winkel kannst du nun mit der Umkehrfunktion des Kosinus berechnen.
Wähle dazu auf dem Taschenrechner die Funktion .
Antwort: Der Winkel zwischen der Flächendiagonalen und der Raumdiagonalen beträgt etwa .
Wie groß ist der Schnittwinkel der Raumdiagonalen und ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Du brauchst den Vektor und seinen Betrag , ebenso den Vektor und seinen Betrag .
Den Winkel berechnest du mit:
↓ Setze die berechneten Werte ein.
↓ Berechne das Skalarprodukt und berechne die Wurzeln.
↓ Vereinfache.
↓ Kürze.
Den Winkel kannst du nun mit der Umkehrfunktion des Kosinus berechnen.
Wähle dazu auf dem Taschenrechner die Funktion .
Antwort: Der Schnittwinkel der Raumdiagonalen und beträgt etwa .
- 6
Gegeben sind die beiden Vektoren , mit und .
Für welche Werte von schließen die beiden Vektoren einen Winkel von ein?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Es ist .
Weiterhin gilt:
↓ Berechne das Skalarprodukt und die Beträge.
↓ Vereinfache.
↓ Ziehe die Wurzel und kürze.
↓ Löse nach auf.
Die Gleichung hat die Lösungen und .
Antwort: Die beiden Vektoren und schließen mit dem Vektor einen Winkel von ein.
Die folgende Abbildung dient nur zur Veranschaulichung:
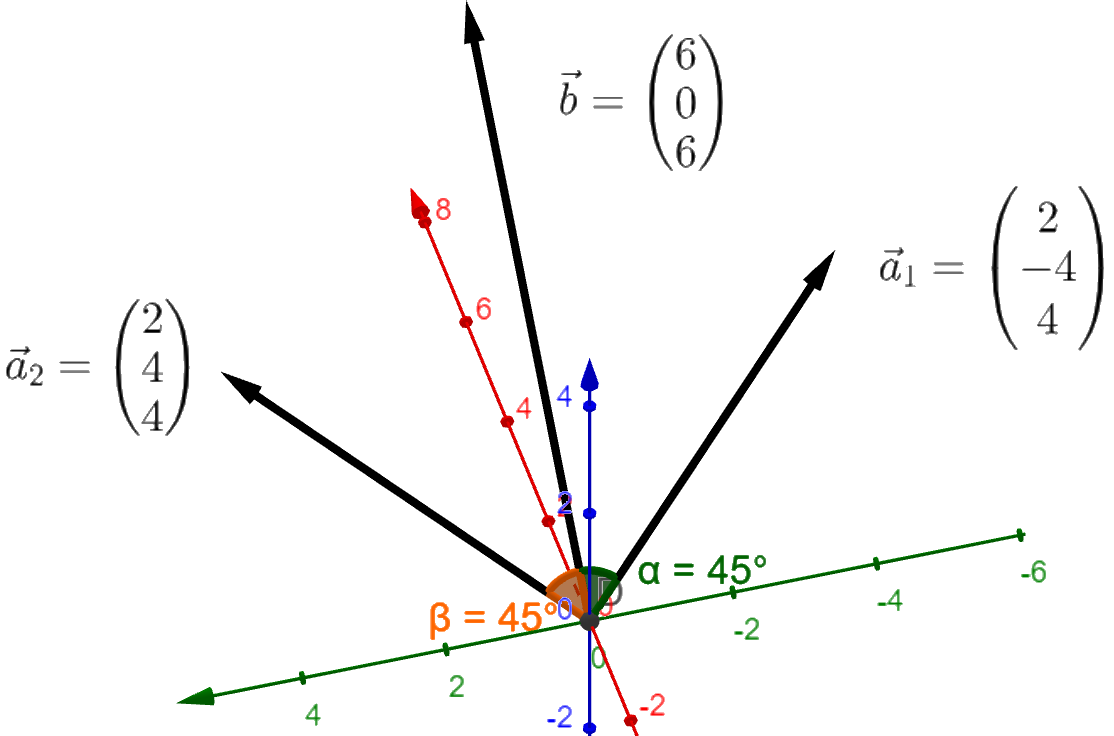
Es ist .
Löse mit den gegebenen Vektoren die Gleichung:
