Analysis, Teil A, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die Funktion f: $x \mapsto l n (x - 3)$ mit maximaler Definitionsmenge $D$ und Ableitungsfunktion $f^{'}$ .
Geben Sie $D$ sowie die Nullstelle von $f$ an. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Definitionsmenge
Definitionsmenge
Was im Logarithmus steht, muss immer größer als $0$ sein.
$\ln (\underset{Das muss größer als 0 sein}{\underset{⏟}{x - 3}})$
$\Rightarrow x - 3 > 0$ bzw. $x > 3$
Die Definitionsmenge ist somit:
$D = {x \in ℝ | x > 3}$
Nullstelle
Die ln-Funktion hat eine Nullstelle für $x = 1$ :
Setze $x - 3 = 1 \Rightarrow x = 4$
Die Funktion $f$ hat für $x = 4$ eine Nullstelle.
Alternative
Die $\ln$ -Funktion wurde durch den Term " $x - 3$ " um drei nach rechts verschoben. Die Nullstelle, die der Graph an der Stelle $x = 1$ normalerweise hätte, befindet sich jetzt bei $x = 4$ .
Das Argument $(x - 3)$ der $\ln$ -Funktion muss größer 0 sein.
Also muss gelten:
$x - 3 > 0$
Somit muss $x > 3$ sein.
Zur Nullstelle: Die $\ln$ -Funktion hat den Wert 0, wenn das Argument $x - 3 = 1$ ist.
Also $f (x) = 0$ , genau dann, wenn $x - 3 = 1$ . Damit ist die Nullstelle (nach Umstellen) $x = 4$ .

Ermitteln Sie diejenige Stelle $x \in D$ für die $f^{'} (x) = 2$ gilt. (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ableitung berechnen
Berechne die erste Ableitung der Funktion $f$ . Beachte die Kettenregel.
$f^{'} (x) = \frac{1}{x - 3} \cdot 1$
Es soll $f^{'} (x) = 2$ sein:
Setze $f^{'} (x) = 2$ .
↓
$2$ $=$ $\frac{1}{x - 3}$ $\cdot (x - 3)$
↓
Löse nach $x$ auf.
$2 \cdot (x - 3)$ $=$ $1$
↓
Löse die Klammer auf.
$2 x - 6$ $=$ $1$ $+ 6$
$2 x$ $=$ $7$ $: 2$
$x$ $=$ $3,5$
$x = 3,5$ ist in $D$ enthalten.
Für $x = 3,5$ hat die erste Ableitung von $f$ den Wert $2$ .

Gegeben ist die in $ℝ$ \{0} definierte Funktion $g : x \mapsto \frac{1}{x^{2}} - 1.$

Geben Sie eine Gleichung der waagrechten Asymptote des Graphen von $g$ sowie die Wertemenge von $g$ an. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Waagrechte Asymptote
Gleichung der waagrechten Asymptote
Bilde den Grenzwert gegen $+ \infty :$
$\lim_{x \to + \infty} \underset{\to 0^{+}}{\underset{⏟}{\frac{1}{\underset{\to + \infty}{\underset{⏟}{x^{2}}}}}} - 1 = - 1^{-}$
Bilde den Grenzwert gegen $- \infty :$
$\lim_{x \to - \infty} \underset{\to 0^{+}}{\underset{⏟}{\frac{1}{\underset{\to + \infty}{\underset{⏟}{x^{2}}}}}} - 1 = - 1^{-}$
$\Rightarrow y = - 1$
$y = - 1$ ist eine waagerechte Asymptote.
Wertemenge
Alle Funktionswerte der Funktion $g$ liegen oberhalb der Asymptoten $y = - 1$ .
Somit ergibt sich die Wertemenge zu:
$W = {y \in ℝ | y > - 1}$ oder $W =] - 1; + \infty [$

Berechnen Sie den Wert des Integrals $\int_{\frac{1}{2}}^{2} g (x) d x .$ (3 P)

3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Eine in $ℝ$ definierte ganzrationale, nicht lineare Funktion $f$ mit erster Ableitungsfunktion $f^{'}$ und zweiter Ableitungsfunktion $f^{''}$ hat folgende Eigenschaften:
$f$ hat bei $x_{1}$ eine Nullstelle
Es gilt $f^{'} (x_{2}) = 0$ und $f^{''} (x_{2}) \neq 0.$
$f^{'}$ hat ein lokales Minimum an der Stelle $x_{3} .$
Die Abbildung 1 zeigt die Postion von $x_{1}$ , $x_{2}$ , und $x_{3}$
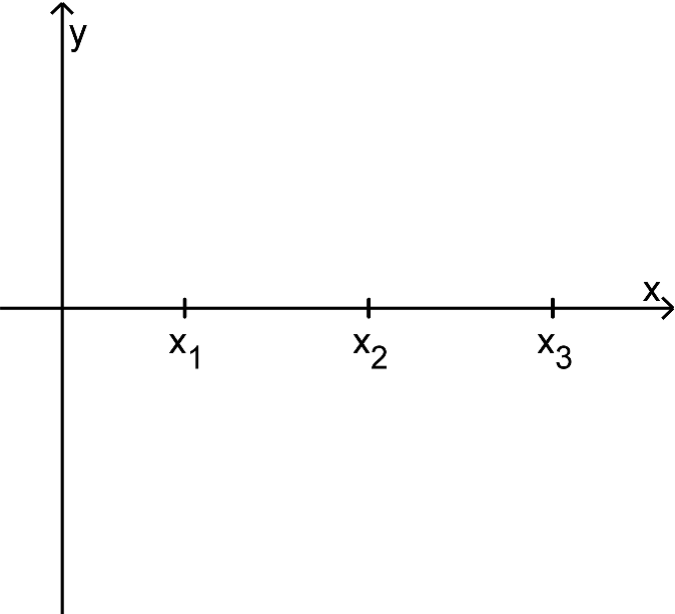
Abb. 1
Begründen Sie, dass der Grad von $f$ mindestens $3$ ist. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkt
Der Grad von $f$ ist mindestens $3$
$f^{'}$ hat ein lokales Minimum an der Stelle $x_{3}$ .
Bei $x_{3}$ liegt somit ein Wendepunkt vor:
Es ist $f^{'} (x_{3}) = 0$ und da bei $x_{3}$ ein lokales Minimum vorliegt, ist $f^{''} (x_{3}) = 0$
(mit einem Vorzeichenwechsel von $f^{''}$ bei $x_{3}$ ).
Die Funktion $f$ hat also einen Wendepunkt und die Gleichung $f^{''} (x) = 0$ hat mindestens eine Lösung. $f^{''}$ muss also mindestens den Grad $1$ haben.
$\Rightarrow f (x)$ hat mindestens den Grad $3$

Skizzieren Sie in Abbildung $1$ einen möglichen Graphen von $f .$ (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
Der Graph der Funktion $f$ könnte z.B. so aussehen.
$($ Hier ist $x_{1} = 1$ , $x_{2} = 2$ und $x_{3} = 3) .$
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
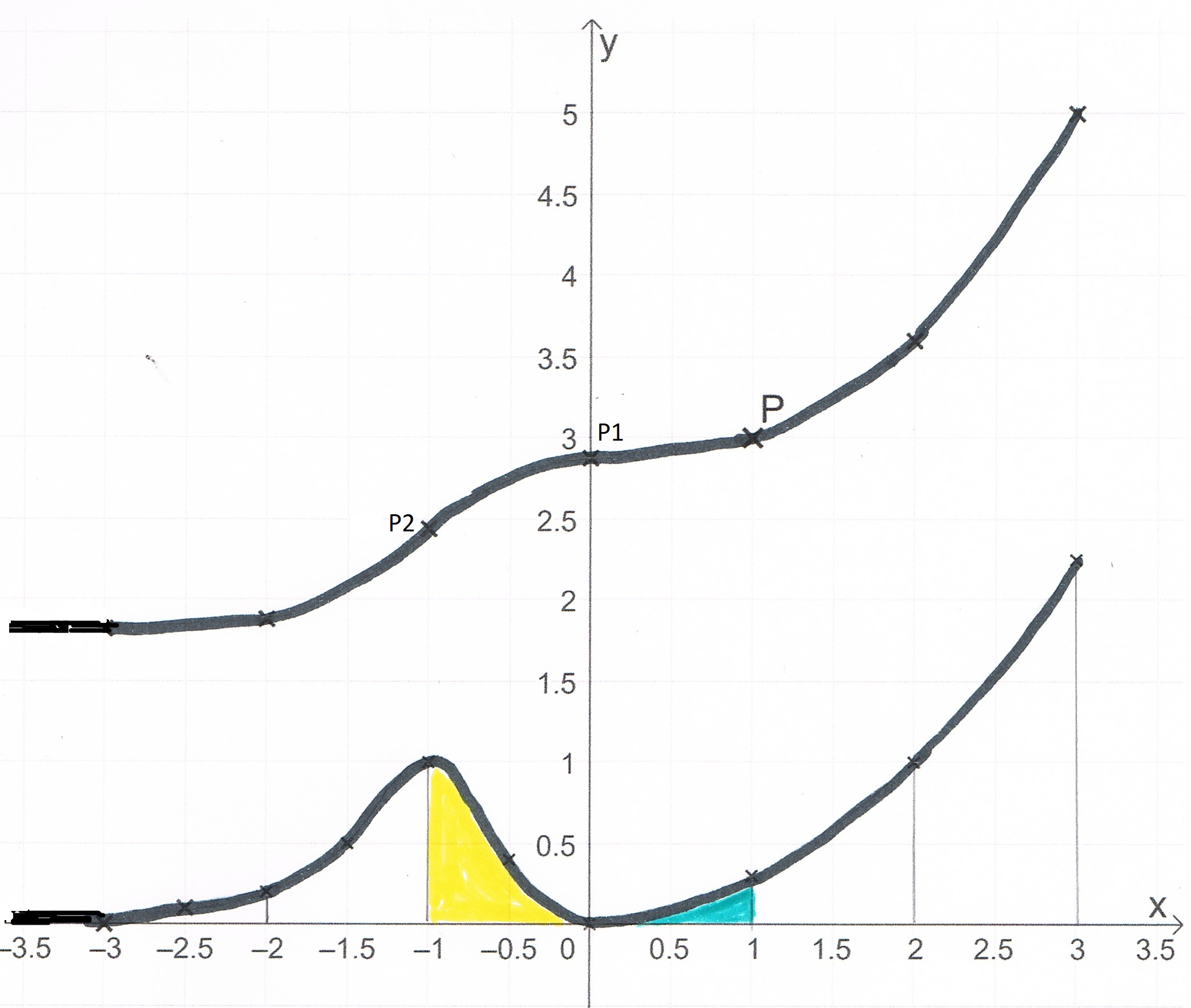
Abbildung 2 zeigt den Graphen der in $ℝ$ definierten Funktion $g$ , dessen einzige Extrempunkte $(- 1 | 1)$ und $(0 | 0)$ sind, sowie den Punkt $P$ .
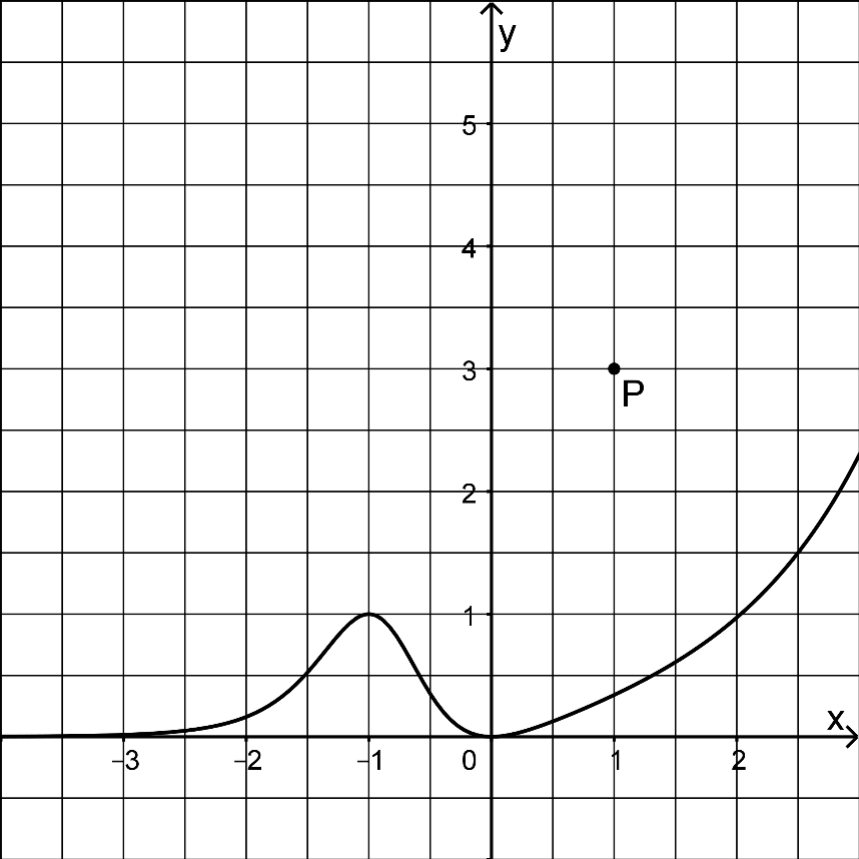
Abb. 2
Geben Sie die Koordinaten des Tiefpunkts des Graphen, der in
$ℝ$ definierten Funktion $h$ mit $h (x) = - g (x - 3)$ an. (2 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extrema
Koordinaten des Tiefpunkts von h(x)
$h (x) = - g (x - 3)$
Die Funktion $h (x)$ geht im ersten Schritt durch Spiegelung von $g (x)$ an der x-Achse hervor. Im zweiten Schritt wird dann $- g (x)$ um $3$ nach rechts verschoben.
Der Graph der Funktion $g (x)$ hat einen Hochpunkt $H P (- 1 | 1)$ und einen Tiefpunkt $T P (0 | 0)$ . Bei der Spiegelung an der x-Achse wird aus dem Hochpunkt ein Tiefpunkt (und aus dem Tiefpunkt wird ein Hochpunkt). Der Graph der gespiegelten Funktion $g (x)$ hat dann den Tiefpunkt $T P (- 1 | - 1)$ . Damit die Funktion $h (x)$ entsteht, muss die gespiegelte Funktion noch um $3$ Einheiten nach rechts verschoben werden, sodass der Tiefpunkt der Funktion $h (x)$ entsteht. $\Rightarrow T P (- 1 + 3 | - 1)$
Der Tiefpunkt hat also die Koordinaten: $T P (2 | - 1)$

Der Graph einer Stammfunktion von $g$ verläuft durch $P$ . Skizzieren Sie diesen Graphen in Abbildung 2. (3 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Stammfunktion
Besondere Punkte des Graphen von $g (x)$
Die Stammfunktion von $g (x)$ ist die Funktion $G (x)$ . Es gilt: $G^{'} (x) = g (x)$
Anhand von ein paar besonderen Punkten von $g (x)$ folgen diese Informationen:
Die Extrempunkte des Graphens der Funktion $g$ sind Wendepunkte des Graphens der Stammfunktion $G$ .
Doppelte Nullstellen des Graphens der Funktion $g$ sind Terrassenstellen des Graphens der Stammfunktion $G$ .
Konkret heißt das:
Der Graph von $G$ hat bei $x = - 1$ eine Wendestelle. Die Steigung im Wendepunkt des Graphens von $G$ beträgt $1$ , da $g$ an der Stelle $x = - 1$ den Funktionswert $1$ hat. Der Funktionswert $1$ ist dann der Wert von $G^{'} (- 1)$ .
Der Graph von $G$ hat bei $x = 0$ eine Terrassenstelle, da der Graph von $g$ bei $x = 0$ eine doppelte Nullstelle hat. Die Steigung im Terrassenpunkt ist $0$ .
Wie findet man nun Funktionswerte der Stammfunktion $G$ ?
Der Punkt $P (1 | 3)$ liegt auf dem Graphen von $G (x)$ . Dieser kann eingezeichnet werden und hilft, weitere Punkte zu berechnen.
Eine Flächeneinheit in der Abbildung 2 des Graphens $g$ besteht aus $4$ Kästchen, d.h. ein Kästchen hat einen Flächeninhalt von $0,25 FE .$
Der türkis eingefärbte Bereich zwischen $x = 0$ und $x = 1$ zwischen dem Graphen von $g$ und der x-Achse ist etwa $0,5$ Kästchen groß:
$\Rightarrow 0,5 \cdot 0,25 = 0,125 FE$
Somit vergrößert sich der Flächeninhalt zwischen $x = 0$ und $x = 1$ um $0,125 FE .$
Im gegebenen Punkt $P$ der Abb. 2 gilt: $G (1) = 3 \Rightarrow G (0) = 3 - 0,125 = 2,875$
Ein zweiter Punkt der Graphens von $G$ hat dann die Koordinaten $P_{1} (0 | 2,875) .$
Der gelb eingefärbte Bereich zwischen $x = - 1$ und $x = 0$ zwischen dem Graphen von $g$ und der x-Achse ist etwa $1,75$ Kästchen groß:
$\Rightarrow 1,75 \cdot 0,25 \approx 0,44 FE$
Somit vergrößert sich der Flächeninhalt zwischen $x = - 1$ und $x = 0$ zwischen dem Graphen von $g$ und der x-Achse um etwa $0,44 FE .$
Im Punkt $P 1$ ist $G (0) = 2,875 \Rightarrow G (- 1) = 2,875 - 0,44 \approx 2,44$
Ein dritter Punkt der Graphens von $G$ hat die Koordinaten $P_{2} (0 | 2,44)$ .
Zusatz
Entsprechend findet man weitere Punkte des Graphens von $G$ , sodass sich nach dem Verbinden der eingezeichneten Punkte der Graph der Stammfunktion $G$ ergibt. (Die Berechnung der Koordinaten der anderen eingezeichneten Punkte wird hier nicht weiter ausgeführt.)
Beim Zeichnen ist noch zu beachten, dass die Steigung im Punkt $P 1$ gleich $0$ und im Punkt $P 2$ gleich $1$ ist.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

Setze $f^{'} (x) = 2$ .
	↓
$2$	$=$	$\frac{1}{x - 3}$	$\cdot (x - 3)$
	↓	Löse nach $x$ auf.
$2 \cdot (x - 3)$	$=$	$1$
	↓	Löse die Klammer auf.
$2 x - 6$	$=$	$1$	$+ 6$
$2 x$	$=$	$7$	$: 2$
$x$	$=$	$3,5$

$\int_{\frac{1}{2}}^{2} (\frac{1}{x^{2}} - 1) d x$	$=$	${[- \frac{1}{x} - x]}_{\frac{1}{2}}^{2}$
	↓	Die Stammfunktion von $\frac{1}{x^{2}}$ ist $- \frac{1}{x}$ . In die Klammer wird für $x$ der obere Wert (2) eingesetzt und minus die Klammer mit dem unteren Wert $(\frac{1}{2})$ gerechnet.
	$=$	$(- \frac{1}{2} - 2) - (- \frac{1}{\frac{1}{2}} - \frac{1}{2})$
	↓	Klammern auflösen.
	$=$	$- \frac{1}{2} - 2 + 2 + \frac{1}{2}$
	↓	Zusammenfassen.
	$=$	$0$

Analysis, Teil A, Aufgabengruppe 1

Definitionsmenge

Nullstelle

Gleichung der waagrechten Asymptote

Wertemenge

Der Grad von f ist mindestens 3

Koordinaten des Tiefpunkts von h(x)

Besondere Punkte des Graphen von g(x)

Wie findet man nun Funktionswerte der Stammfunktion G?

Zusatz

Der Grad von $f$ ist mindestens $3$

Besondere Punkte des Graphen von $g (x)$

Wie findet man nun Funktionswerte der Stammfunktion $G$ ?