Aufgabengruppe I
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen
Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
(Kleine Änderungen der Formulierung aufgrund der Umwandlung in ein digitales Medium sind kursiv geschrieben.)
- 1
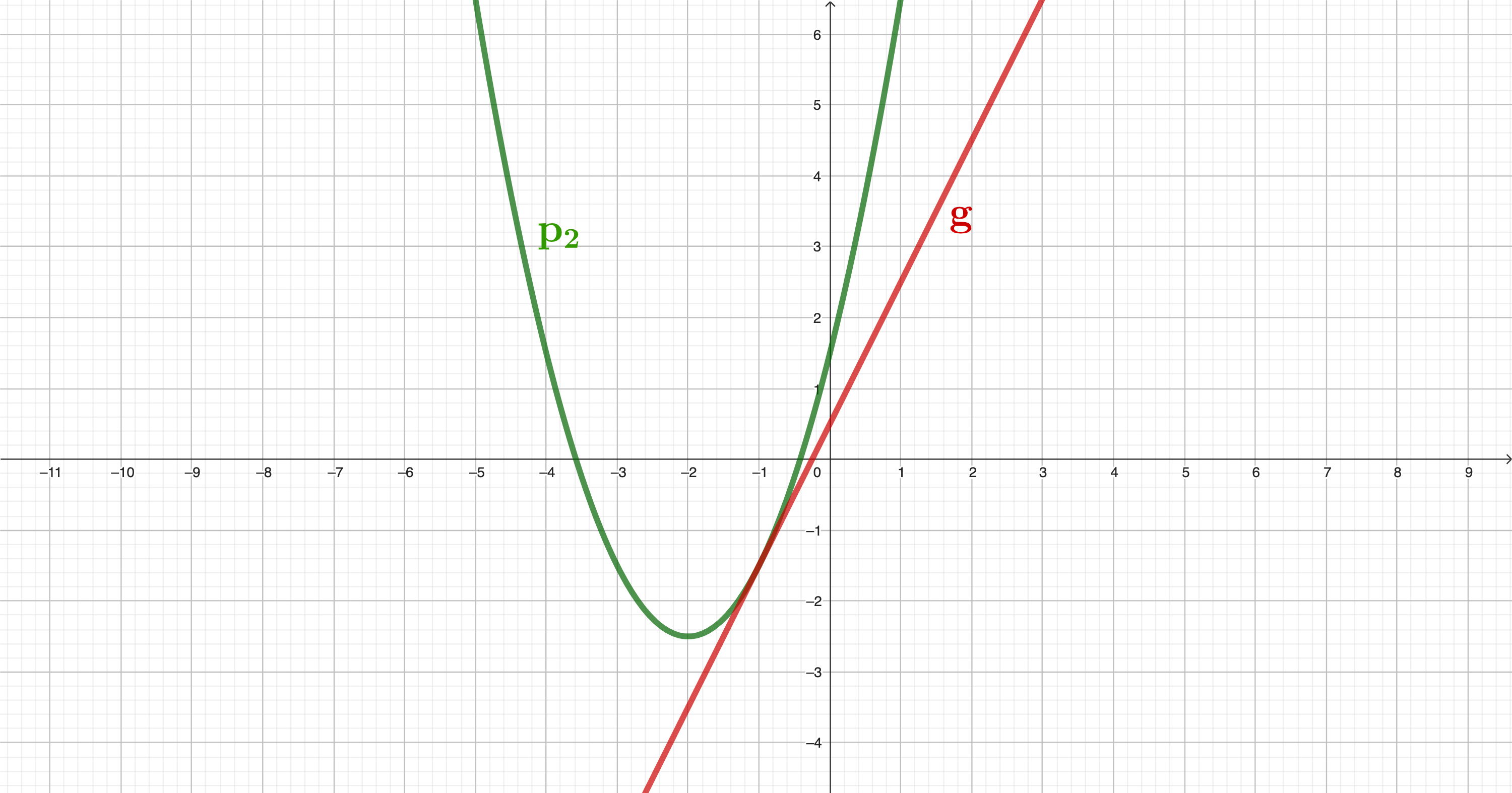
Die nachfolgende Abbildung zeigt den Graphen einer Normalparabel .
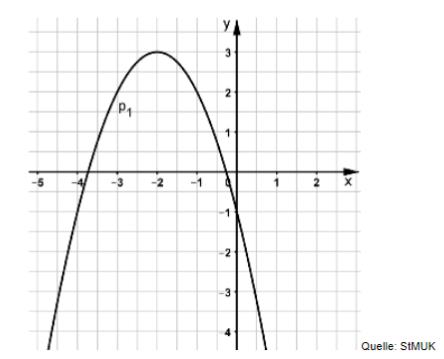
Ermitteln Sie rechnerisch die Funktionsgleichung von in der Normalform.
Überprüfen Sie durch Rechnung, ob die Punkte und auf der Normalparabel mit der Funktionsgleichung : liegen.
Ermitteln Sie rechnerisch den Scheitelpunkt der Parabel .
Die Gerade g mit der Funktionsgleichung hat mit der Parabel den Punkt gemeinsam. Berechnen Sie die Koordinaten von und geben Sie diesen Punkt an.
Zeichnen Sie die Graphen der Parabel und der Geraden in ein Koordinatensystem mit der Längeneinheit .
Eine nach unten geöffnete Normalparabel hat den Scheitelpunkt . Durch Spiegelung an der y-Achse entsteht . Durch eine weitere Spiegelung von an der x-Achse entsteht . Geben Sie die Funktionsgleichung der Parabel in der Scheitelpunktform an und stellen Sie Ihren Lösungsweg nachvollziehbar dar.
- 2
Das radioaktive Element Kobalt-60 hat eine Halbwertszeit von fünf Jahren.
In einem Behälter befinden sich 3,675 kg Kobalt-60. Berechnen Sie, wie viele Kilogramm nach 13 Jahren von dieser Menge noch vorhanden sind.
Ermitteln Sie rechnerisch, nach wie vielen Jahren von den 3,675 kg Kobalt-60 nur noch 0,1 kg vorhanden sind.
Berechnen Sie die Ausgangsmenge des radioaktiven Elements Kobalt-60, von der nach 38 Jahren noch 0,742 kg vorhanden sind.
- 3
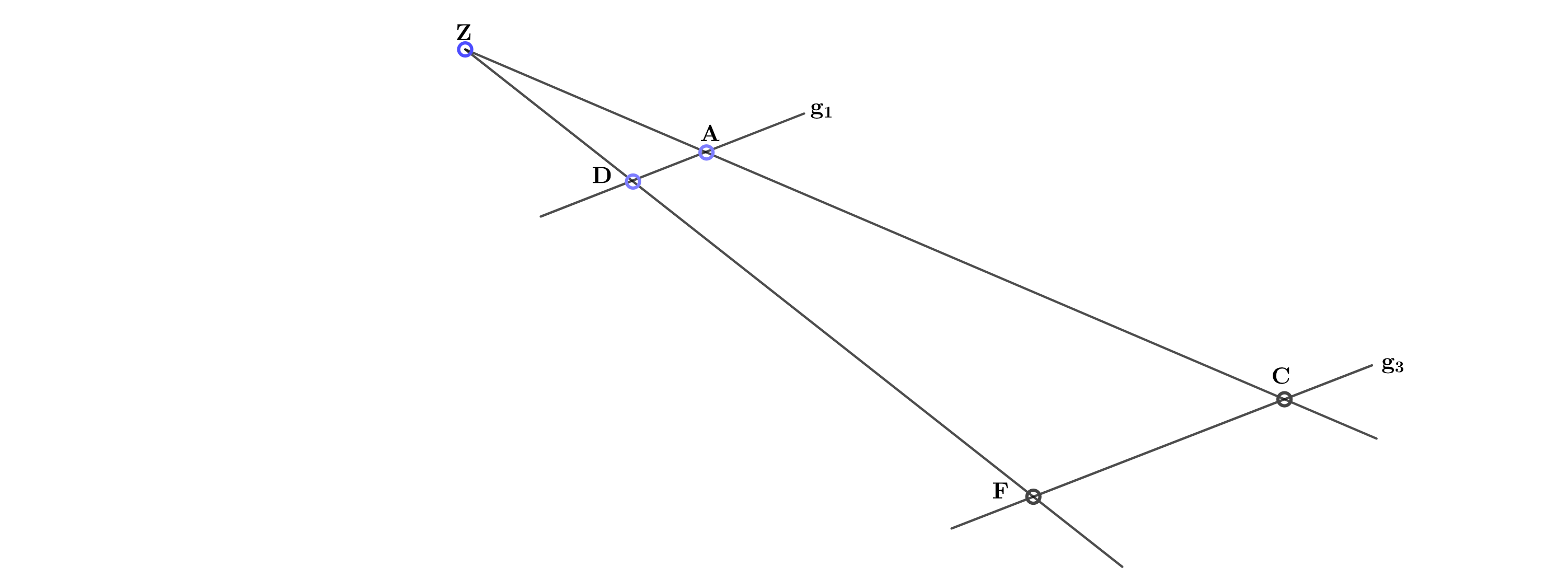
In der folgenden Skizze gilt: ; ; ; .
Berechnen Sie die Länge der Strecke in cm.
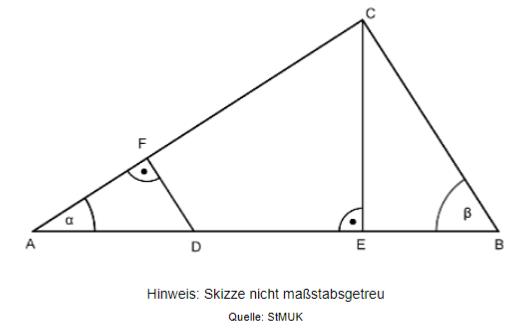 cm
cm - 4
Vereinfachen Sie den unten stehenden Term so weit wie möglich. Es gilt:
- 5
Lösen Sie folgende Aufgaben.
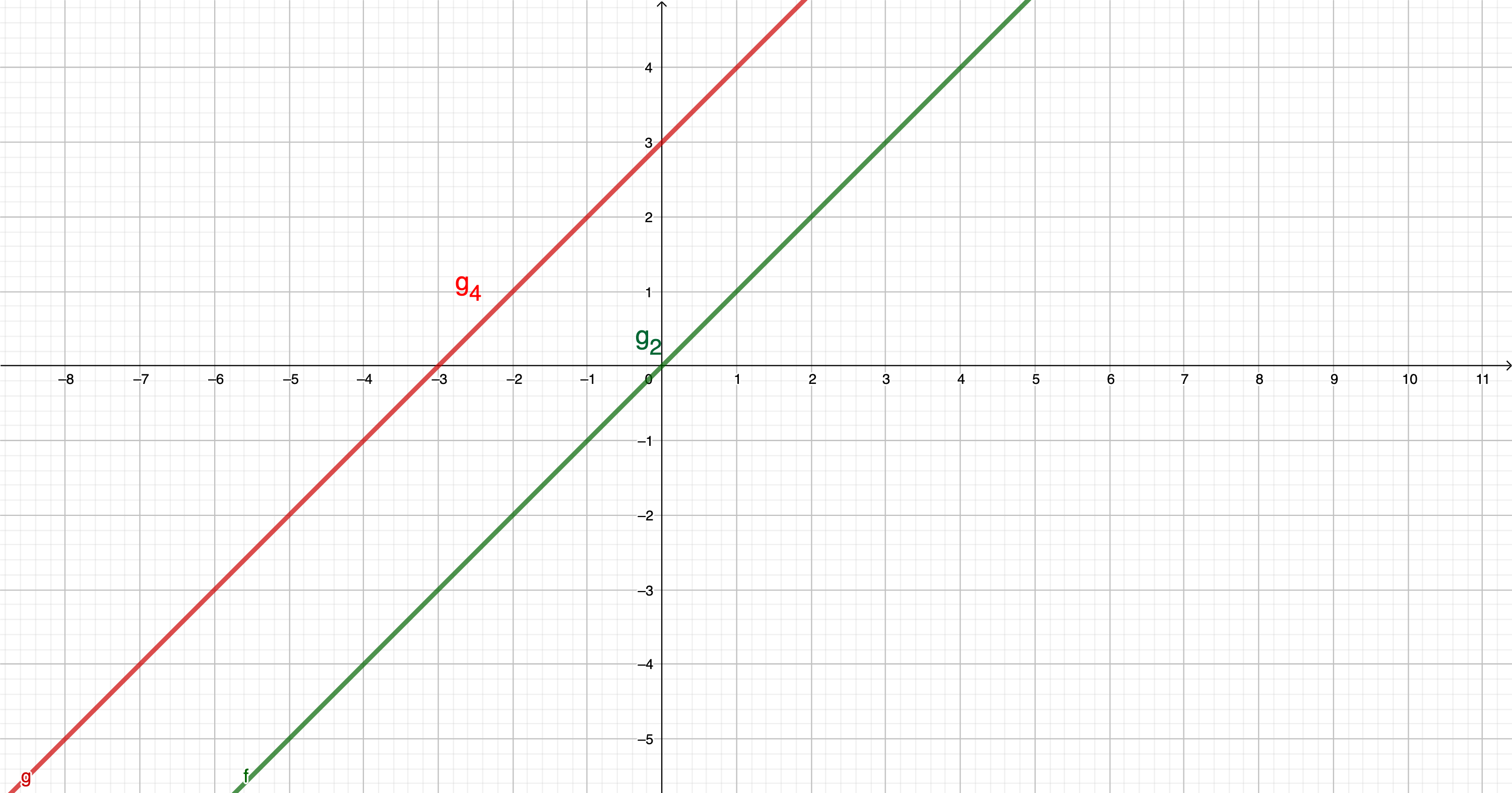
Bestimmen Sie rechnerisch die Funktionsgleichung der Geraden , die durch die Punkte und verläuft.
Die Gerade verläuft durch den Punkt und steht senkrecht auf der Geraden : . Bestimmen Sie rechnerisch die Funktionsgleichung der Geraden .
Geben Sie eine mögliche Funktionsgleichung einer Geraden an, die parallel zur Geraden : verläuft und nicht auf liegt.
Der Punkt liegt auf der Geraden : . Bestimmen Sie die Steigung rechnerisch.
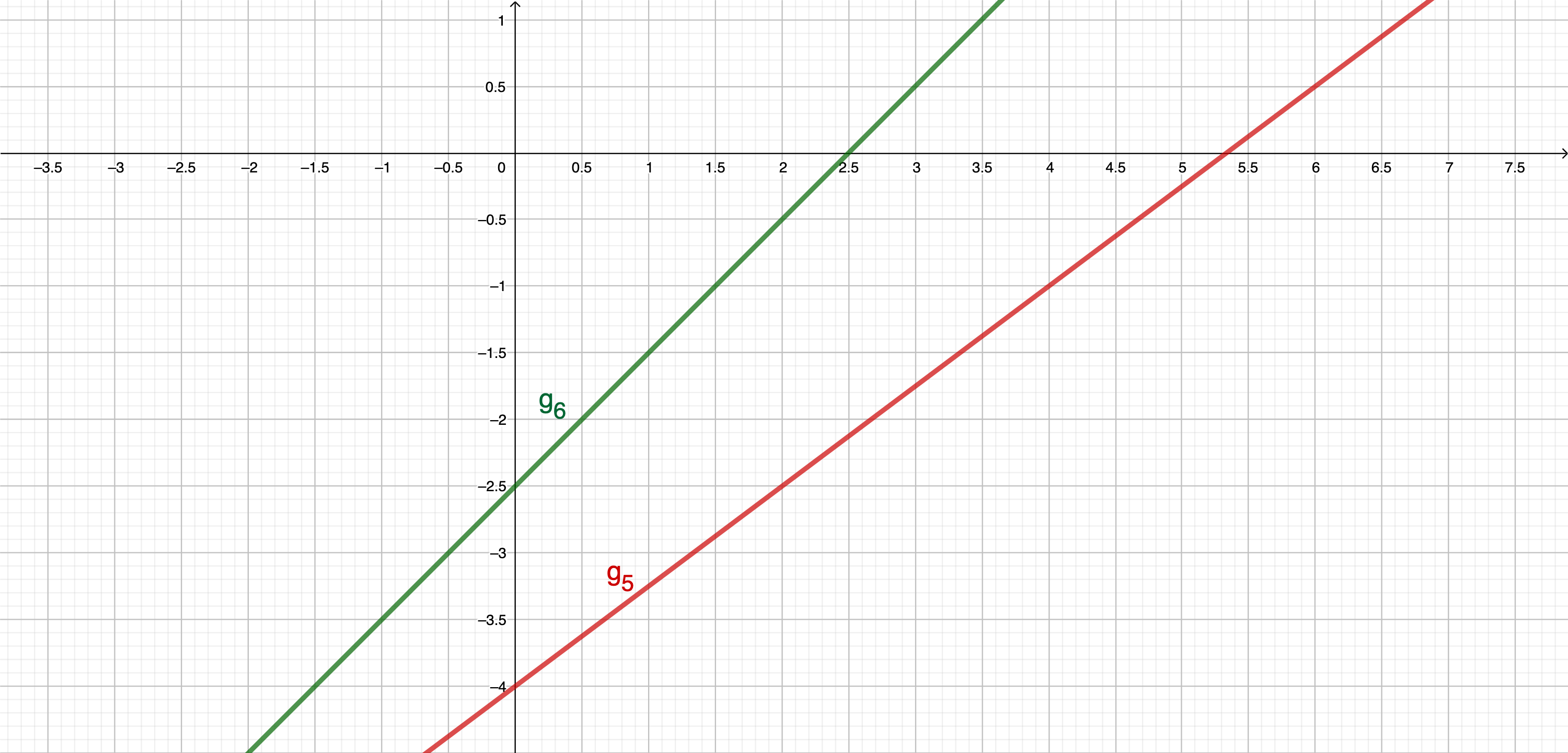
Die Gerade : und die Gerade mit der Funktionsgleichung
: schneiden sich im Punkt . Ermitteln Sie rechnerisch die Koordinaten des Schnittpunkts und geben Sie diesen Punkt an.
Zum Beispiel so: "(3|-2,5)"
Berechnen Sie die Koordinaten des Schnittpunkts der Geraden mit der x-Achse und geben Sie diesen Punkt an.
Zum Beispiel so: "(3|-2,5)"
Zeichnen Sie die Geraden und in ein Koordinatensystem mit der Längeneinheit 1cm.
- 6
Lösen Sie die folgende Gleichung rechnerisch. Geben Sie die Definitionsmenge und die Lösungsmenge an.
- 7
Eine Metallkugel mit einem Durchmesser von 40 mm soll eingeschmolzen und zu sechs gleich großen Kugeln umgeformt werden.
Zeigen Sie durch Rechnung, dass die sechs kleineren Kugeln zusammen einen größeren Oberflächeninhalt haben als die ursprüngliche Kugel.
- 8
Es gilt .
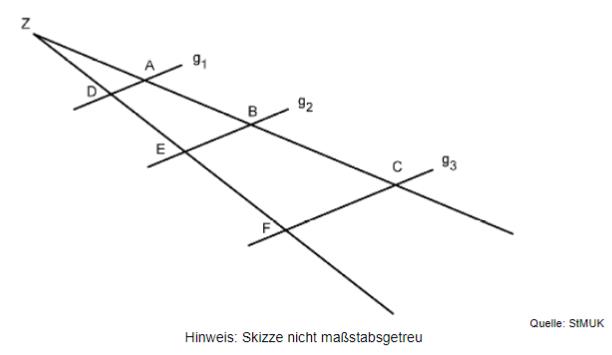
Von den folgenden vier Aussagen geben zwei die Streckenverhältnisse richtig wieder.
Berechnen Sie die Länge der Strecke , wenn folgende Streckenlängen gegeben sind: ; ; .
- 9
Folgende Aufgaben sind Anwendungen von binomischen Formeln und quadratischen Gleichungen.
Ersetzen Sie die Symbole , und jeweils durch den entsprechenden Term und schreiben Sie die mathematisch richtige Gleichung auf Ihr Lösungsblatt.
(1)
(2) =
Ersetzen Sie die Platzhalter der folgenden Gleichung so, dass eine quadratische Gleichung mit der Lösungsmenge L = {-4; 3} entsteht und schreiben Sie diese auf Ihr Lösungsblatt.
- 10
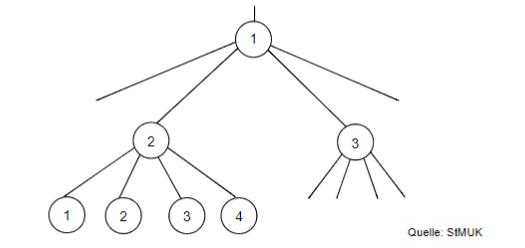
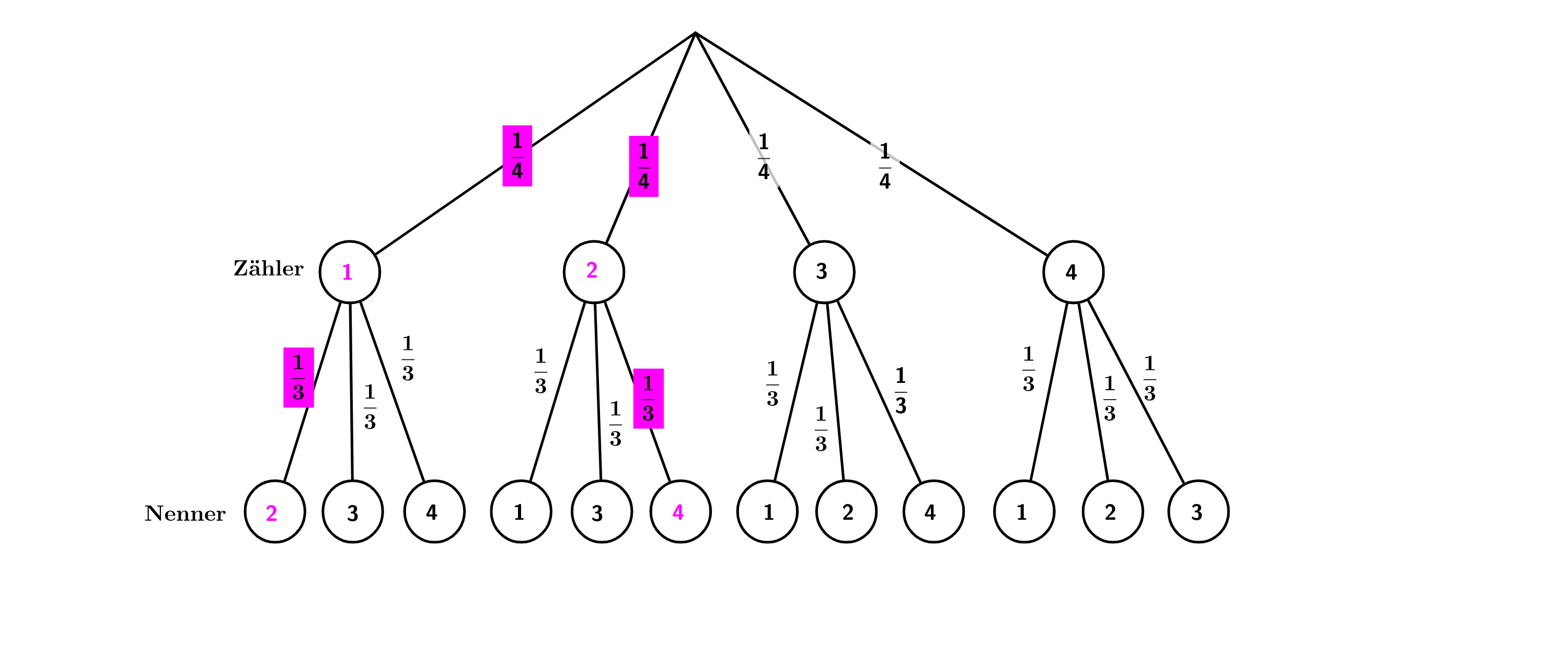
In einem Behälter befinden sich genau vier Kugeln. Sie sind mit den Ziffern 1, 2, 3 und 4 durchnummeriert.
Mit den vier Kugeln kann man unterschiedliche Zahlen legen. Ermitteln Sie rechnerisch die Anzahl aller Kombinationsmöglichkeiten für eine vierstellige Zahl.
Es werden nacheinander zwei Kugeln gezogen und nicht mehr zurückgelegt. Aus beiden gezogenen Ziffern wird ein Bruch gebildet. Die zuerst gezogene Ziffer bildet den Zähler, die zweite den Nenner des Bruches. Geben Sie die Ergebnismenge mit allen bei diesem Vorgang möglichen Brüchen an und bestimmen Sie die Wahrscheinlichkeit, dass der gebildete Bruch den Wert 0,5 hat.
Die Abbildung zeigt einen Ausschnitt aus einem Baumdiagramm zu einem weiteren Zufallsexperiment. Begründen Sie, dass das Experiment mit Zurücklegen der Kugeln durchgeführt wurde.