Nachtermin Teil B
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen
Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgaben findest Du hier zum Ausdrucken als PDF.
- 1
Die Parabel verläuft durch die Punkte und . Sie hat eine Gleichung der Form mit und . Die Gerade hat die Gleichung mit .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
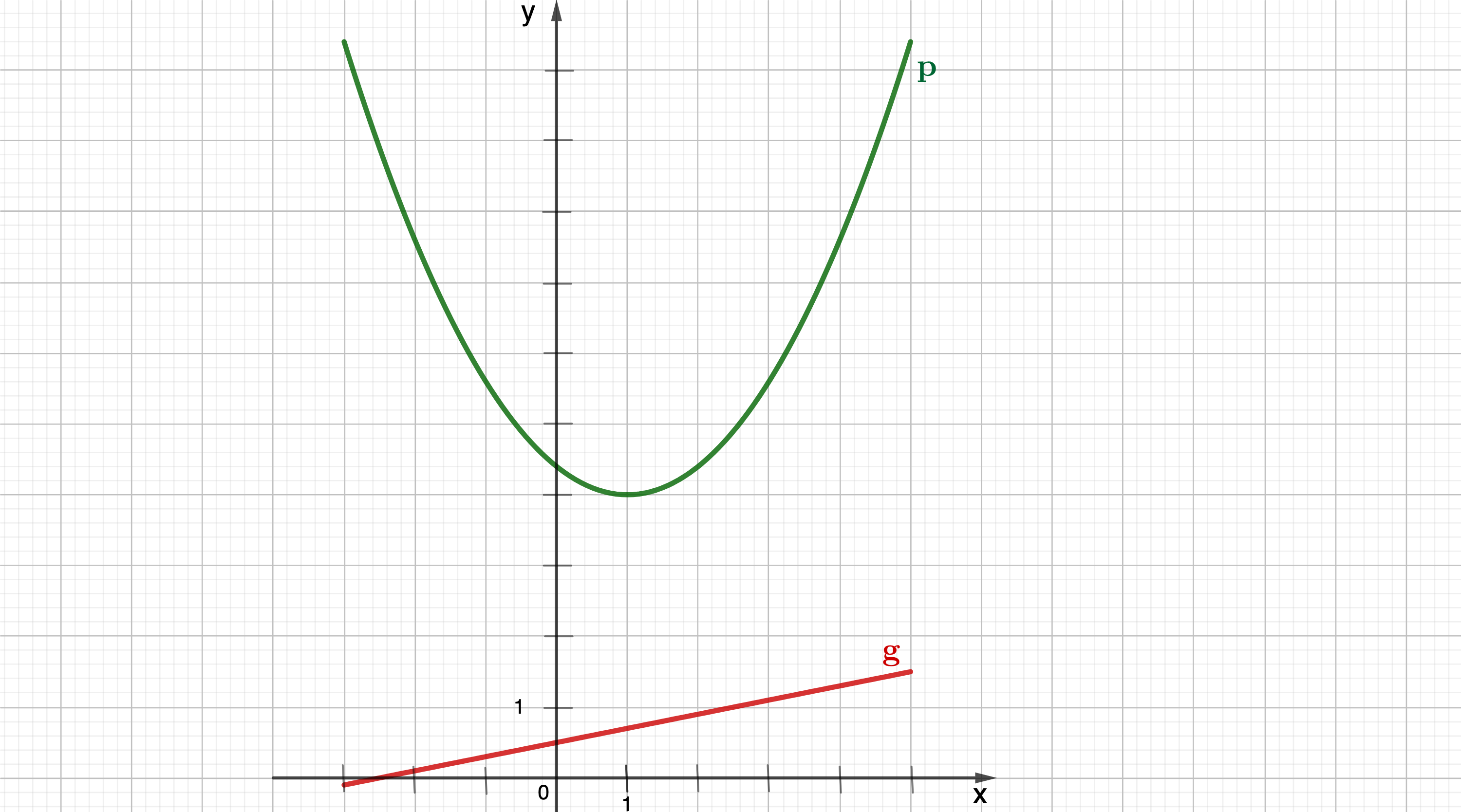
Zeigen Sie durch Berechnung der Werte für b und c, dass die Parabel p die Gleichung hat.
Zeichnen Sie sodann die Gerade g sowie die Parabel p für in ein Koordinatensystem ein.
Für die Zeichnung: Längeneinheit 1 cm;
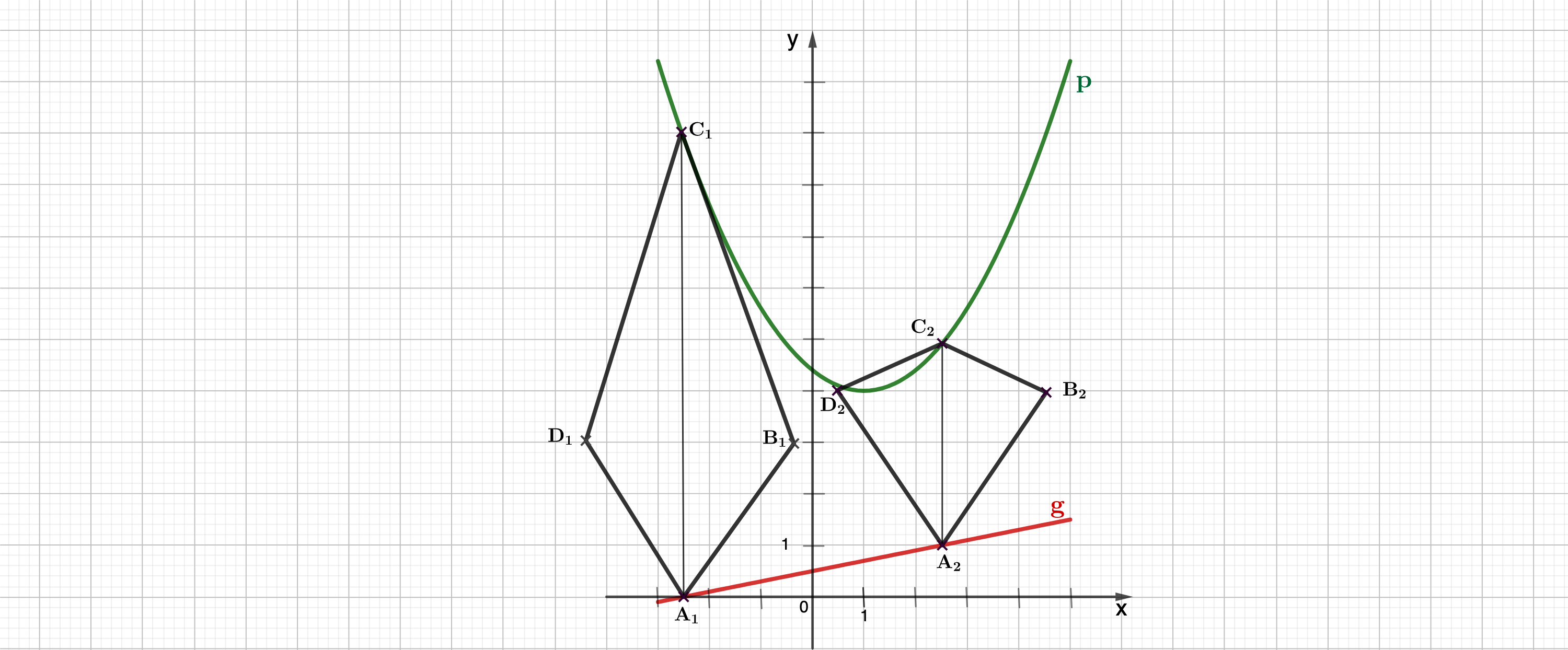
Punkte und sind zusammen mit Punkten auf der Geraden g und Punkten auf der Parabel p die Eckpunkte von Drachenvierecken mit den Geraden als Symmetrieachse.
Es gilt: .
Zeichnen Sie das Drachenviereck für und das Drachenviereck für in das Koordinatensystem zu Teilaufgabe (a) ein.
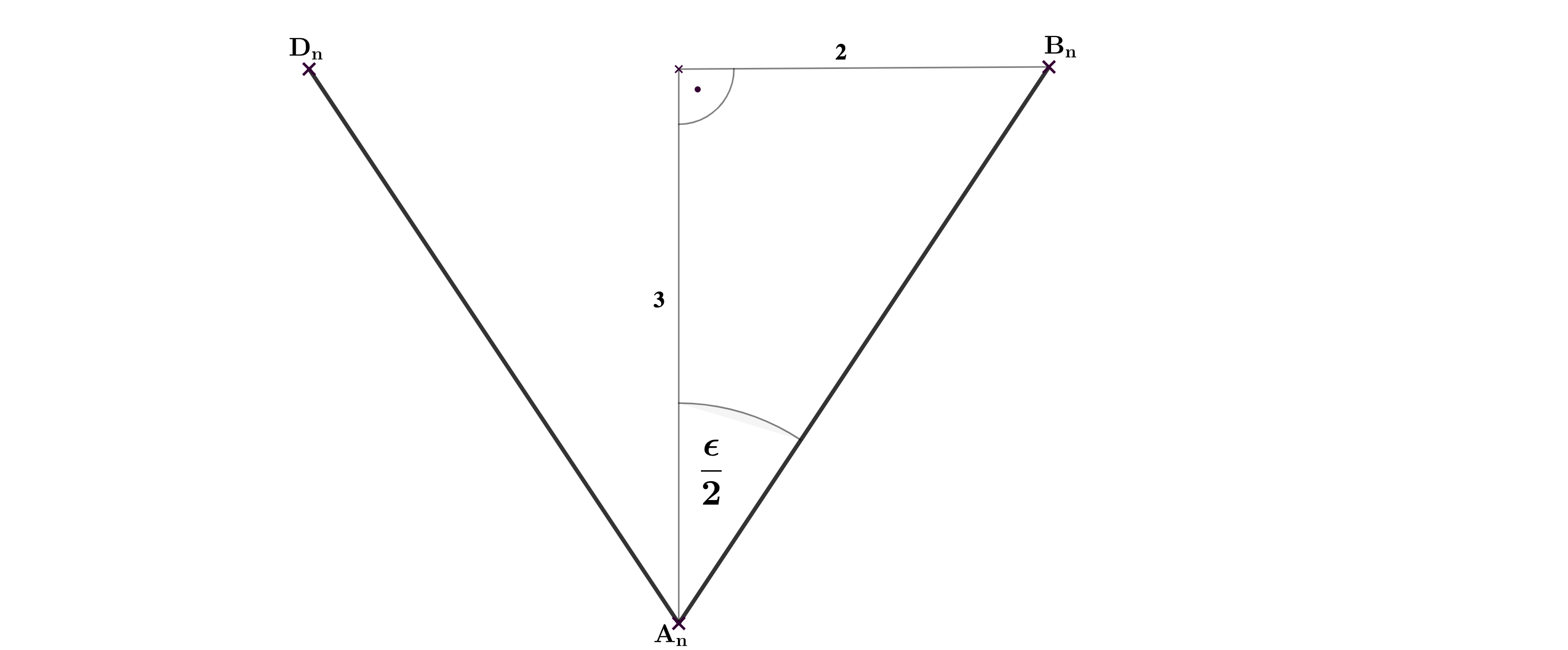
In allen Drachenvierecken haben die Winkel das gleiche Maß . Berechnen Sie das Maß der Winkel .
Zeigen Sie rechnerisch, dass für den Flächeninhalt A der Drachenvierecke in Abhängigkeit von der Abszisse x der Punkte gilt: [Teilergebnis: ]
Unter den Drachenvierecken hat das Drachenviereck den minimalen Flächeninhalt.
Berechnen Sie den Flächeninhalt des Drachenvierecks und den zugehörigen Wert für .
Begründen Sie, dass für die Drachenvierecke Rauten sind.
Ermitteln Sie die -Werte der Punkte und .
Zeigen Sie durch Rechnung, dass die Punkte und nicht gemeinsam auf einer Geraden liegen können.
- 2
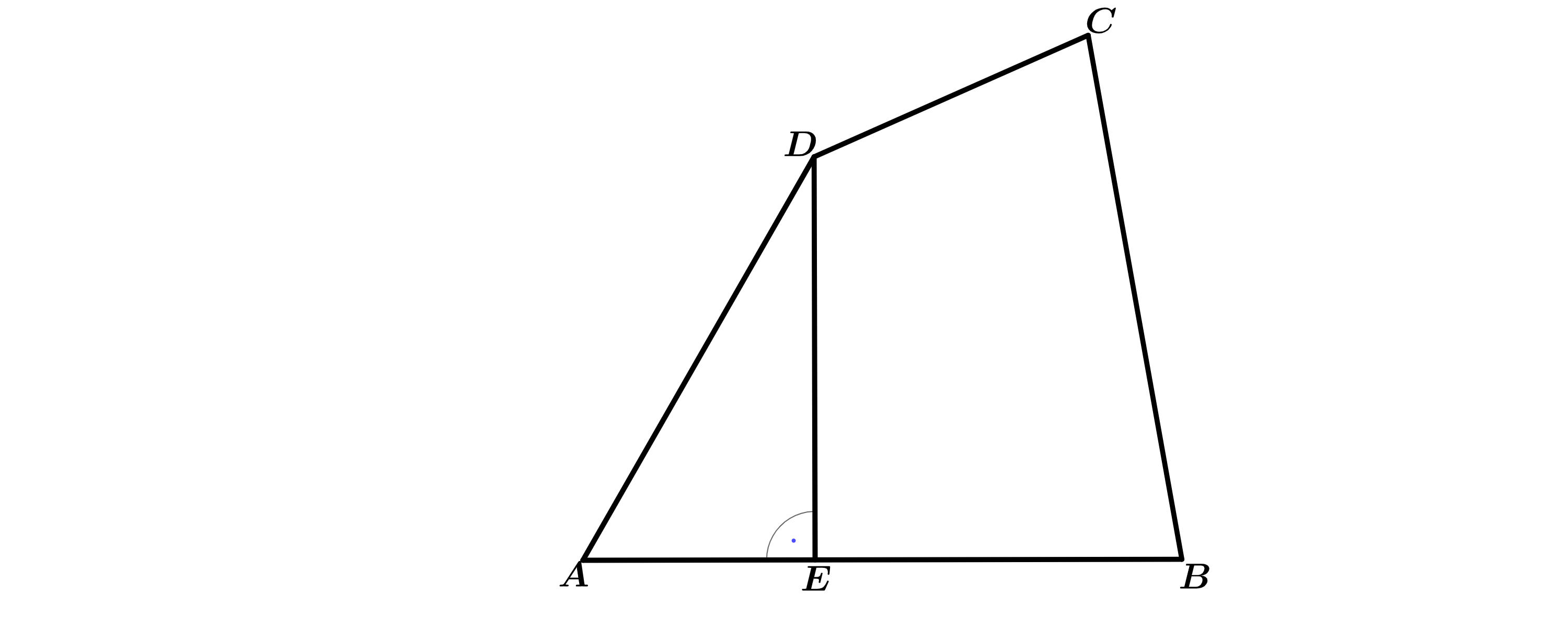
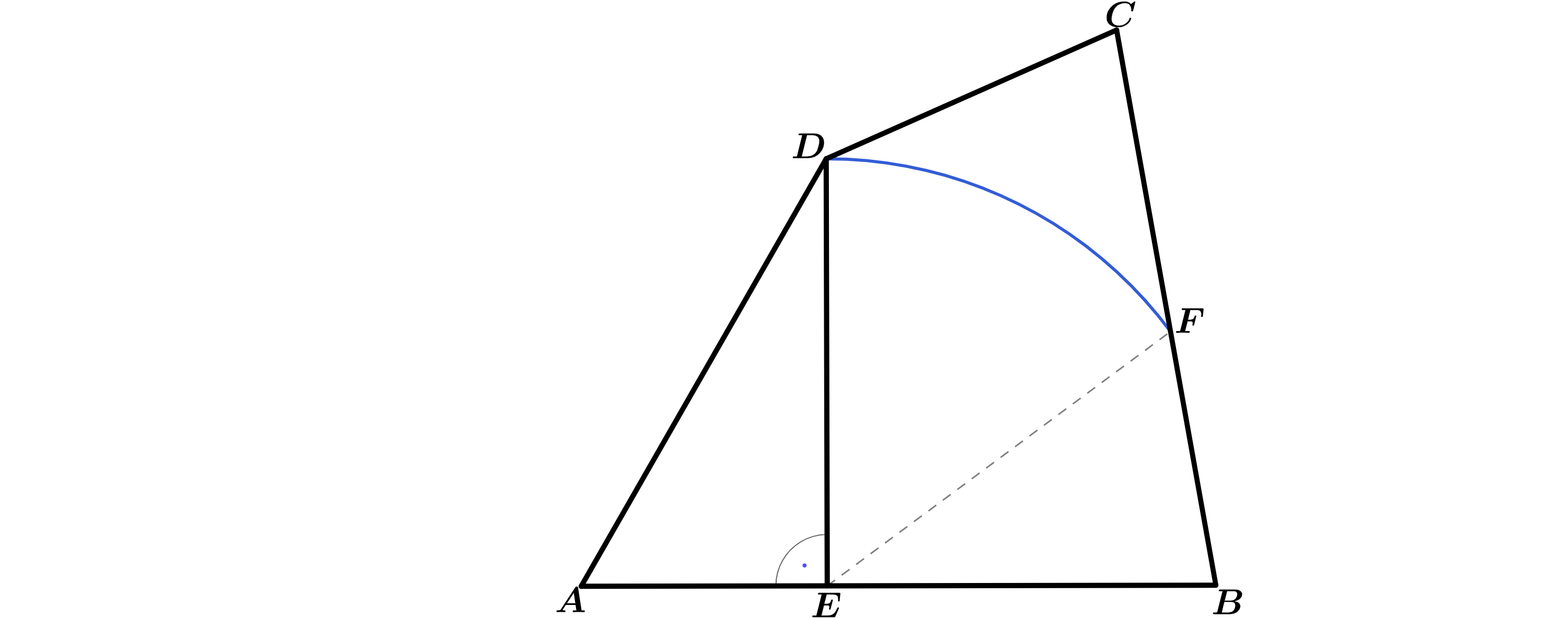
Die untenstehende Skizze zeigt den Plan eines Gartengrundstücks .
Es gilt: ; ;
; ; .
Runden Sie im Folgenden auf eine Stelle nach dem Komma.
Zeichnen Sie das Viereck im Maßstab .
Die dreieckige Gartenfläche die im Plan durch die Strecken und begrenzt ist, soll geschottert werden. Eine Metallschiene, im Plan durch gekennzeichnet, soll verhindern, dass sich der Schotter im ganzen Grundstück verteilt. Zum Nachbargrundstück wird entlang der im Plan durch gekennzeichneten Strecke ein Sichtschutz errichtet. Berechnen Sie die Länge der Strecken und .
[Teilergebnis: ]
Die im Plan durch das Viereck dargestellte Fläche soll aus einem Rasenstück und einem Beet bestehen.
Bestimmen Sie rechnerisch die Länge der Strecke [EC] sowie den Flächeninhalt des Vierecks .
[Ergebnis: ; Teilergebnis: ]
Der Kreis mit dem Mittelpunkt E hat den Radius und schneidet die Strecke [BC] im Punkt F. Das Beet wird durch den Kreisbogen sowie durch die Strecken und begrenzt. Zeichnen Sie den Kreisbogen in die Zeichnung zur Teilaufgabe (a) ein.
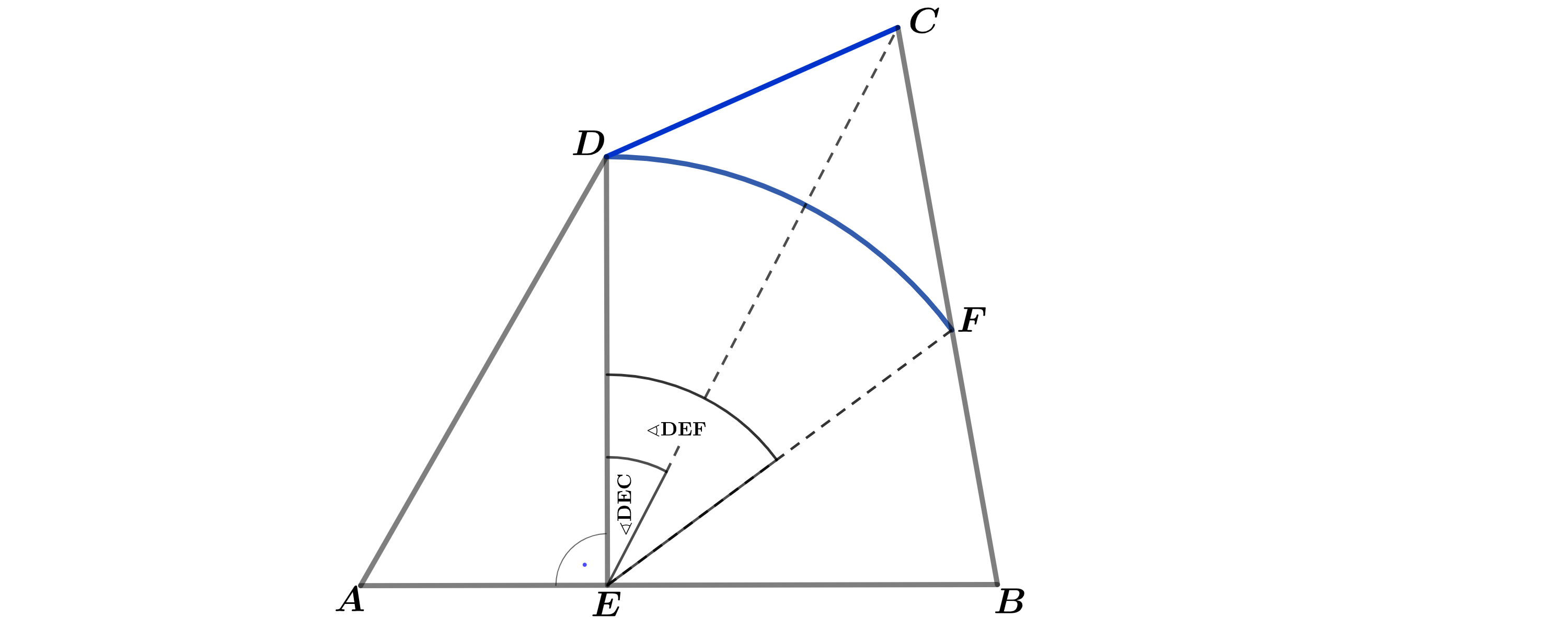
Das Beet aus Teilaufgabe (d) wird entlang des Kreisbogens und der Strecke [DC] mit einem Schneckenschutzzaun geschützt. Berechnen Sie die benötigte Länge des Zauns.
[Teilergebnis: ]
Berechnen Sie den Flächeninhalt des Beetes.