Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
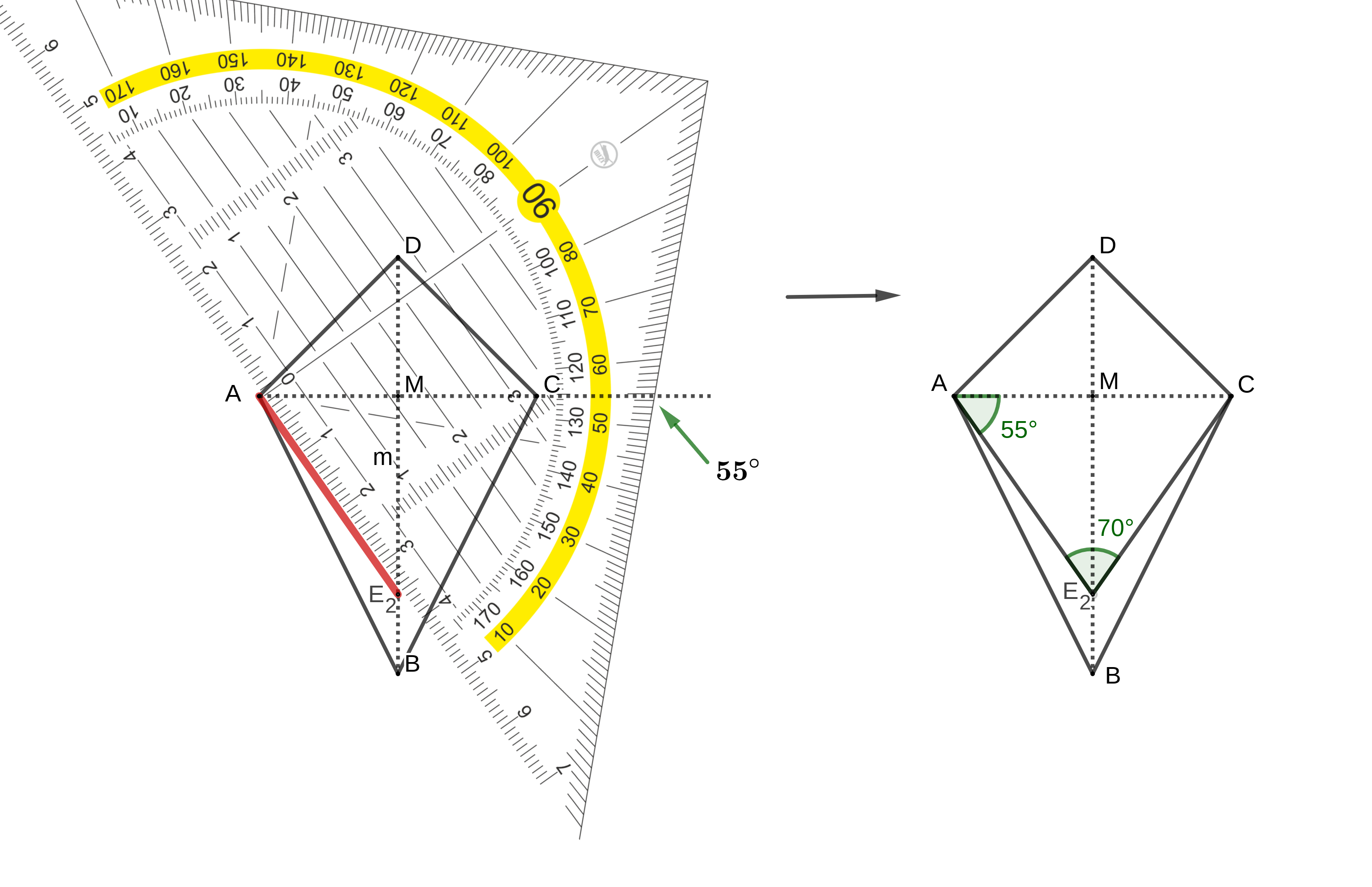
Gegeben ist das Drachenviereck $A B C D$ mit der Symmetrieachse $B D$ und dem Diagonalenschnittpunkt $M$ .
Es gilt: $A M = D M = 2 cm$ und $B D = 6 cm$ .
Punkte $E_{n}$ auf der Strecke $[B M]$ legen zusammen mit den Punkten $A, C$ und die Drachenvierecke $A E_{n} C D$ fest.
Die Winkel $C E_{n} A$ haben das Maß $φ$ mit $φ \in [{53,13}^{\circ}; 180^{\circ} [.$
Die Zeichnung zeigt das Drachenviereck $A B C D$ und das Drachenviereck $A E_{1} C D$ für $φ = 100^{\circ}$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Zeichnen Sie das Drachenviereck $A E_{2} C D$ für $φ = 70^{\circ}$ in die Zeichnung zur Aufgabenstellung ein. Bestätigen Sie sodann die untere Intervallgrenze für $φ$ durch Rechnung.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
Zunächst versuchst du die Lage des Punktes $E_{2}$ so zu konstruieren, dass für $φ$ ein $70 °$ Winkel entsteht. In einem Dreieck beträgt die Summe der Innenwinkel immer $180 °$ . Das Dreieck $A C E_{2}$ ist gleichschenklig, die Winkel $∠ E_{2} A C$ und $∠ A C E_{2}$ sind also gleich groß. Für die Winkelsumme erhältst du nun $180 ° = 70 ° + 2 \cdot ∠ E_{2} A C$ und damit $∠ E_{2} A C = 55 °$ . Mit diesem Winkel kannst du jetzt den Punkt $E_{2}$ , wie unten gezeigt, bestimmen.
Je weiter der Punkt $E$ nach unten wandert, desto spitzer wird der Winkel $φ$ . Am kleinsten ist $φ$ also, wenn der Punkt $B$ erreicht ist. Das Dreieck $A B M$ ist rechtwinklig, deshalb kannst du hier gut den Tangens verwenden und erhältst:
$\tan (\frac{φ}{2}) = \frac{A M}{M B} = \frac{2}{4} = \frac{1}{2}$
Mit deinem Taschenrechner und der Umkehrfunktion des Tangens bekommst du als Ergebnis: $φ = 53,13$ .

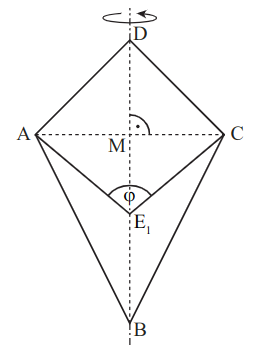
Die Drachenvierecke $A E_{n} C D$ rotieren um die Gerade $B D$ . Zeigen Sie, dass für das Volumen $V$ der entstehenden Rotationskörper in Abhängigkeit von $φ$ gilt:
$V (φ) = \frac{8}{3} \cdot π \cdot (1 + \frac{1}{\tan (0,5 \cdot φ)}) {cm}^{3}$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
Der Rotationskörper besteht aus zwei Kegeln, die dieselbe Grundfläche, aber verschiedene Höhen haben. Das Volumen des Körpers ist also die Summe der beiden Kegelvolumen.
Allgemein gilt:
$V_{Kegel} = \frac{1}{3} \cdot G \cdot h = \frac{1}{3} \cdot r^{2} \cdot π \cdot h$
Die Grundfläche ist ein Kreis mit dem Radius $A M = 2$ . Er hat den Flächeninhalt:
$A_{Kreis} = 2^{2} \cdot π = 4 π$
Der obere Kegel hat die Höhe $M D = 2$ . Damit kannst du sein Volumen bestimmen:
$V_{oberer Kegel} = \frac{1}{3} \cdot 4 π \cdot 2 = \frac{8}{3} π$
Der untere Kegel hat die Höhe $E_{n} M$ , die Länge dieser Strecke ist von der Größe des Winkels $φ$ abhängig. In dem rechtwinkligen Dreieck $A E_{n} M$ gilt:
$\tan (\frac{φ}{2}) = \frac{A M}{E_{n} M} = \frac{2}{E_{n} M}$
Durch Umstellen der Gleichung erhältst du: $E_{n} M = \frac{2}{\tan (\frac{φ}{2})}$
Das Volumen des unteren Kegels ist also:
$V_{unterer Kegel} = \frac{1}{3} \cdot 4 π \cdot \frac{2}{\tan (\frac{φ}{2})} = \frac{8}{3} π \cdot \frac{1}{\tan (\frac{φ}{2})}$
Wenn du nun die Summe bildest und dann ausklammerst, entsteht das Volumen des Rotationskörpers: $V_{Rotationskörper} = V_{oberer Kegel} + V_{unterer Kegel}$
$V_{Rotationskörper} = \frac{8}{3} π + \frac{8}{3} π \cdot \frac{1}{\tan (\frac{φ}{2})} = \frac{8}{3} π (1 + \frac{1}{\tan (\frac{φ}{2})})$

Das Drachenviereck $A E_{3} C D$ ist ein Quadrat. Bestimmen Sie das Volumen des zugehörigen Rotationskörpers.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Rotationskörper
In einem Quadrat hat jeder Innenwinkel den Wert $90 °$ , also gilt für das Quadrat auch $φ = 90 °$ . Das kannst du nun in die Formel aus Teilaufgabe b) einsetzen und erhältst:
$\begin{array}{rcll} V_{Rotationskörper} & = & \frac{8}{3} π (1 + \frac{1}{\tan (\frac{90 °}{2})}) \\ = & \frac{8}{3} π (1 + \frac{1}{\tan (45 °)}) \\ = & \frac{16}{3} π \end{array}$
Das Volumen des Rotationskörpers des Quadrats beträgt also $\frac{16}{3} π {cm}^{3} \approx 16,76 {cm}^{3}$ .
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
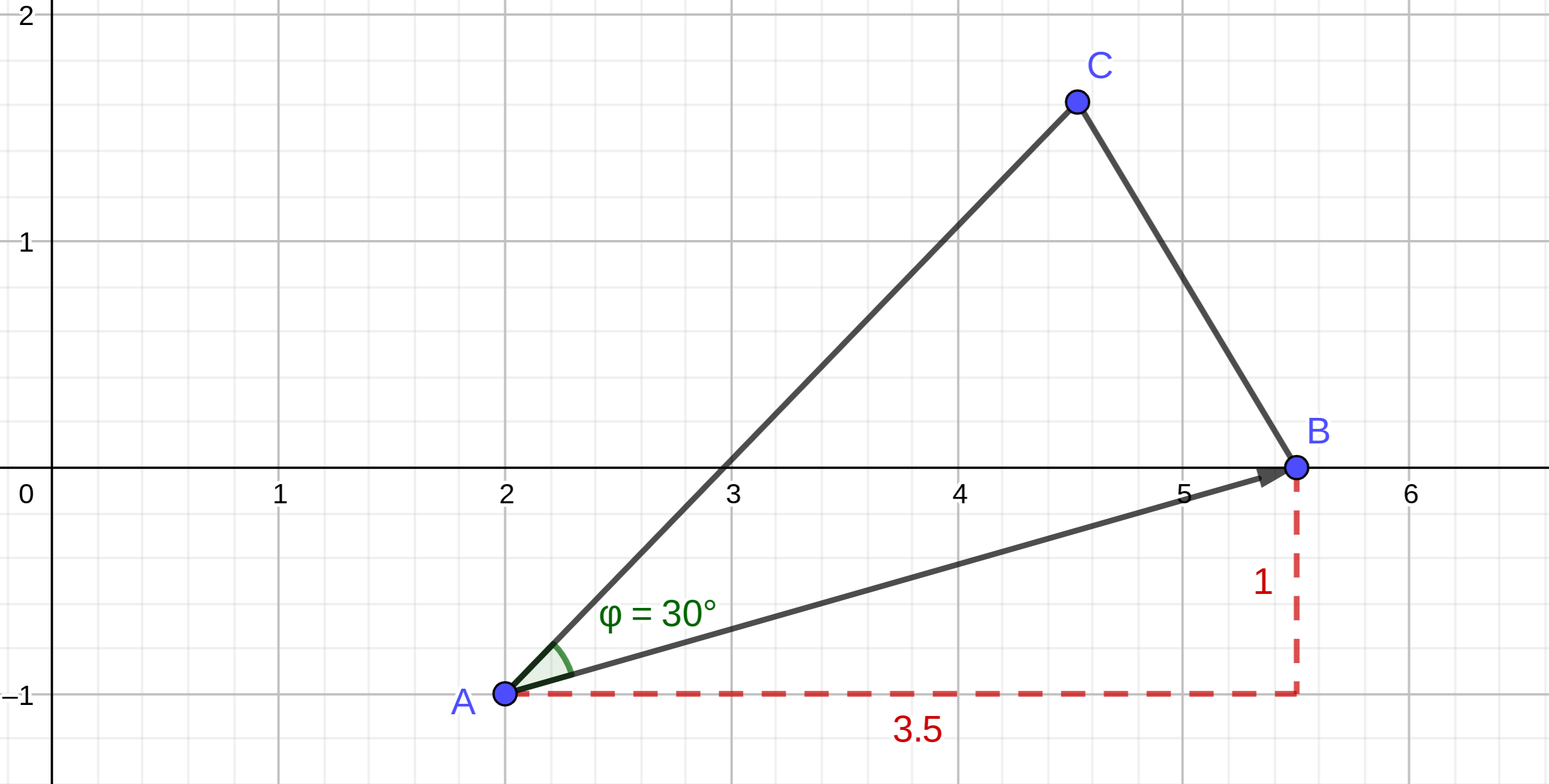
Der Punkt $A (2 | - 1)$ legt zusammen mit den Pfeilen
$\vec{A B_{n}} (φ) = (\begin{array}{c} - 3 \cdot \sin (φ) + 2 \\ 2 \cdot \sin (φ) + 2 \end{array})$
und Punkten $C_{n}$ gleichschenklige Dreiecke $A B_{n} C_{n}$ mit den Basen $[B_{n} C_{n}]$ fest
$(φ \in [0^{\circ}; 360^{\circ}])$ . Es gilt: $∠ B_{n} A C_{n} = 30^{\circ}$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
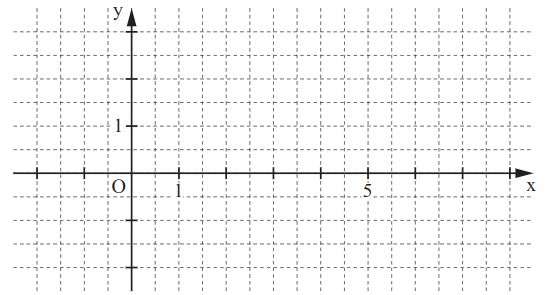
Berechnen Sie die Koordinaten des Pfeils $\vec{A B_{1}}$ für $φ = 210^{\circ}$ und zeichnen Sie das zugehörige Dreieck $A B_{1} C_{1}$ in das Koordinatensystem zur Aufgabenstellung ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie
Um die Koordinaten des Pfeils zu berechnen setzt du einfach den Wert $210 °$ für $φ$ in die Formel ein (achte darauf, dass dein Taschenrechner richtig eingestellt ist):
$\vec{A B_{1}} (φ) = (\begin{array}{c} - 3 \cdot \sin (210 °) + 2 \\ 2 \cdot \sin (210 °) + 2 \end{array}) = (\begin{array}{c} - 3 \cdot (- 0,5) + 2 \\ 2 \cdot (- 0,5) + 2 \end{array}) = (\begin{array}{c} 3,5 \\ 1 \end{array}) .$
Nun kannst du den Pfeil $\vec{A B_{1}}$ in das Koordinatensystem einzeichnen und seine Länge abmessen ( $3,64$ cm). Den Punkt $C_{1}$ kannst du einzeichnen, indem du dein Geodreieck am Punkt $A$ anlegst, am Pfeil $\vec{A B}$ einen $30 °$ Winkel abmisst und dann eine Strecke zeichnest, die genau so lang ist wie $\vec{A B}$ .

Bestimmen Sie rechnerisch die Koordinaten der Punkte $C_{n}$ in Abhängigkeit von $φ$ .
[Ergebnis: $C_{n} (- 3,60 \cdot \sin (φ) + 2,73 | 0,23 \cdot \sin (φ) + 1,73)]$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie
Der Punkt $C_{n}$ besitzt die selben Koordinaten wie der Pfeil $\vec{O C_{n}}$ (Ortsvektor).
Vom Ursprung $O$ aus kommst du zu $C_{n}$ , indem du erst den Punkt $A$ besuchst und dann daran den Pfeil $\vec{A C_{n}}$ hängst. Es gilt also: $\vec{O C_{n}} = \vec{O A} + \vec{A C_{n}}$ .
Die Koordinaten von $A (2 | - 1)$ kennst du bereits. Der Pfeil $\vec{A C_{n}}$ entsteht durch Drehung des Pfeils $\vec{A B_{n}}$ um $A$ mit $∠ B_{n} A C_{n} = 30^{\circ}$ .
$\begin{array}{rcl} \vec{A C_{n}} & = & (\begin{array}{cc} \cos 30 ° & - \sin 30 ° \\ \sin 30 ° & \cos 30 ° \end{array}) \cdot \vec{A B_{n}} \\ = & (\begin{array}{cc} 0,866 & - 0,5 \\ 0,5 & 0,866 \end{array}) \cdot (\begin{array}{c} - 3 \cdot \sin (φ) + 2 \\ 2 \cdot \sin (φ) + 2 \end{array}) \\ = & (\begin{array}{c} - 2,60 \cdot \sin (φ) + 1,73 - \sin (φ) - 1 \\ - 1,5 \sin (φ) + 1 + 1,73 \sin (φ) + 1,73 \end{array}) \\ \vec{A C_{n}} & = & (\begin{array}{c} - 3,60 \cdot \sin (φ) + 0,73 \\ 0,23 \cdot \sin (φ) + 2,73 \end{array}) \end{array}$
Jetzt kannst du noch $\vec{O C_{n}}$ berechnen:
$\begin{array}{rcl} \vec{O C_{n}} & = & \vec{O A} + \vec{A C_{n}} \\ = & (\begin{array}{c} 2 \\ - 1 \end{array}) + (\begin{array}{c} - 3,60 \cdot \sin (φ) + 0,73 \\ 0,23 \cdot \sin (φ) + 2,73 \end{array}) \\ = & (\begin{array}{c} - 3,60 \cdot \sin (φ) + 2,73 \\ 0,23 \cdot \sin (φ) + 1,73 \end{array}) \end{array}$
Damit ist das Endergebnis $C_{n} (- 3,60 \cdot \sin (φ) + 2,73 | 0,23 \cdot \sin (φ) + 1,73)$ .

Für welches Maß von $φ$ wird die Abszisse der Punkte $C_{n}$ minimal? Kreuzen Sie an.
0°
45°
90°
180°
270°

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie
Die Abszisse von $C_{n}$ ist $x = - 3,60 \cdot \sin (φ) + 2,73$ .
Sie wird kleiner, je größer $\sin (φ)$ ist (negativer Faktor vor dem $\sin (φ)$ ).
Der größte Wert, der hier für $\sin (φ)$ möglich ist, ist $1$ (beachte auch die Angabe: $(φ \in [0^{\circ}; 360^{\circ}])$ ).
Diesen Wert erhältst du für einen Winkel von $90 °$ (das kannst du dir zum Beispiel mithilfe des Einheitskreises erklären).
Die Abszisse ist also für einen Winkel von $90 °$ minimal.
Hier kannst du dir noch die verschiedenen Dreiecke für die verschiedenen Winkel ansehen:
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.

Für $φ \in [0^{\circ}; 120^{\circ}]$ gibt es das Dreieck $A B_{2} C_{2}$ , dessen Punkt $C_{2}$ auf der $y$ -Achse liegt. Berechnen Sie die Koordinaten des Punktes $B_{2}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie
Da $C_{2}$ auf der $y$ -Achse liegt, ist die Abszisse von $C_{2}$ gleich $0$ . Es muss also gelten:
$\begin{array}{rcll} - 3,60 \sin (φ) + 2,73 & = & 0 & | - 2,73 \\ - 3,60 \sin (φ) & = & - 2,73 & | : (- 3,60) \\ \sin (φ) & = & 0,76 \end{array}$
Wenn du darauf nun die Umkehrfunktion des Sinus anwendest, erhältst du $φ = 49,32 °$ .
Die Koordinaten von $B_{2}$ erhältst du, indem du dich vom Punkt $A$ aus in Richtung $\vec{A B_{2}}$ bewegst:
$\begin{array}{rcl} \vec{O B_{2}} & = & \vec{O A} + \vec{A B_{2}} \\ = & (\begin{array}{c} 2 \\ - 1 \end{array}) + (\begin{array}{c} - 3 \cdot \sin (49,32 °) + 2 \\ 2 \cdot \sin (49,32 °) + 2 \end{array}) \\ = & (\begin{array}{c} 2 \\ - 1 \end{array}) + (\begin{array}{c} - 3 \cdot 0,76 + 2 \\ 2 \cdot 0,76 + 2 \end{array}) \\ = & (\begin{array}{c} 2 \\ - 1 \end{array}) + (\begin{array}{c} - 2,28 + 2 \\ 1,52 + 2 \end{array}) \\ \vec{O B_{2}} & = & (\begin{array}{c} 1,72 \\ 2,52 \end{array}) \end{array}$
Damit besitzt der Punkt $B_{2}$ die Koordinaten $B_{2} (1,72 | 2,52)$ .
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Vitamin D kann im menschlichen Körper produziert werden, wenn Sonnenstrahlung unter bestimmten Bedingungen auf die Haut trifft. Im Winterhalbjahr nimmt daher die Konzentration von Vitamin D im Körper normalerweise ab.
Bei Andreas wurde Ende September eine Anfangskonzentration von $55$ Nanogramm Vitamin D pro Milliliter Blut $(55 \frac{ng}{ml})$ gemessen. Der Zusammenhang zwischen der Anzahl $x$ der Wochen und der verbleibenden Konzentration $y \frac{ng}{ml}$ an Vitamin D lässt sich bei Andreas näherungsweise durch die Funktion $f_{1}$ mit der Gleichung
$y = 55 \cdot {0,93}^{x} (𝔾 = ℝ^{+} \times ℝ^{+})$ beschreiben.
Um wie viel Prozent reduziert sich folglich bei Andreas die Konzentration an Vitamin D in einer Woche?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktionen
Die Vitamin-D-Konzentration beträgt zu Beginn der Messung $55 \frac{ng}{ml}$ .
Nach einer Woche $(x = 1)$ beträgt sie $0,93 = 93 %$ .
Antwort: Die Konzentration hat um $7 %$ abgenommen.

Berechnen Sie mithilfe der Funktion $f_{1}$ die Konzentration an Vitamin D bei Andreas nach 21 Tagen.
Runden Sie auf 2 Nachkommastellen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktionen
Antwort: Nach $21$ Tagen, also $x = 3$ Wochen beträgt die Konzentration bei Andreas:
$55 \cdot {0,93}^{3} \approx 44,24 \frac{ng}{ml}$

Berechnen Sie, in welcher Woche sich die Anfangskonzentration an Vitamin D bei Andreas entsprechend der Funktion $f_{1}$ halbiert.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktionen
$\begin{array}{rcll} 0,5 \cdot 55 & = & 55 \cdot {0,93}^{x} & | : 55 \\ 0,5 & = & {0,93}^{x} \\ x & = & \log_{0,93} 0,5 \\ x & \approx & 9,55 \end{array}$
Da es keine "halben" Wochen gibt, muss man hier aufrunden.
Achtung: hier gelten die Rundungsregeln nicht, es muss nach dem jeweiligen Kontext entschieden werden!
Antwort: In der 10. Woche hat sich die Vitamin-D-Konzentration halbiert.

Bei Stephan wurde gleichzeitig mit Andreas eine Messung begonnen. Bei Stephan lässt sich der Zusammenhang zwischen der Anzahl $x$ der Wochen und der verbleibenden Konzentration $y \frac{ng}{ml}$ an Vitamin D durch die Funktion $f_{2}$ mit der Gleichung $y = 51 \cdot {0,91}^{x} (𝔾 = ℝ_{0}^{+} \times ℝ_{0}^{+})$ beschreiben.
Ist es unter diesen Voraussetzungen möglich, dass die Konzentrationen an Vitamin D zu einem Zeitpunkt bei Stephan und Andreas den gleichen Wert erreichen? Begründen Sie Ihre Entscheidung ohne Rechnung.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Exponentialfunktionen
Die Vitamin-D-Konzentrationen bei Stephan und Andreas können zu keinem Zeitpunkt gleich sein. Denn die beiden Exponentialfunktionen sind streng monoton fallend.
Für $x = 0$ ist die Konzentration bei Andreas $f_{1} (0) = 55$ und bei Stephan $f_{2} (0) = 51$ . Da also die Startkonzentration bei Stephan niedriger ist als bei Andreas, und die Konzentration bei Stephan schneller fällt als bei Andreas, können beide Vitamin-D-Konzentrationen nie gleich sein.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org