Teil B

Nebenstehende Skizze zeigt das Fünfeck $A B C D E$ , das aus dem Drachenviereck $A B C D$ mit der Symmetrieachse $A C$ und dem Dreieck $A D E$ besteht. Es gilt: $A B = A D = 11 cm; ∡ B A D = 45 °; ∡ C B A = ∡ A D C = ∡ B A E = 90 °; [A B] | | [E D]$ . Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

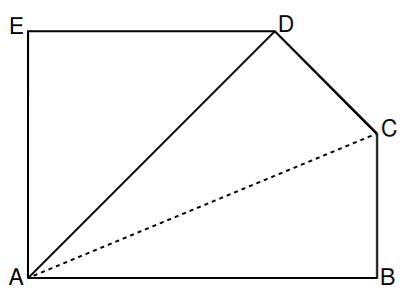
Zeichnen Sie das Fünfeck $A B C D E$ sowie die Strecken $[A D]$ und $[A C]$ .
Teilaufgabe a
Zeichnung des Fünfecks ABCDE
$[A B] = 11 cm$
$∡ ABC$ $= 45 °$
$[A D] = 11 cm$
45°-Winkel
Da [AB] parallel zu $[E D]$ ist, kann man eine Parallele $i$ , durch den Punkt $D$ konstruieren. Die Gerade $j$ steht senkrecht auf $[A B]$ .
Punkt $E$ ist der Schnittpunkt der Geraden $i$ und $j$ .
$∡ ADC$ = 90°
Winkelhalbierende $[A C [$ halbiert den Winkel $∡ BAD$
Punkt $C$ ist der Schnittpunkt der Winkelhalbierenden und der Halbgeraden $[D C [$ .
Strecke $[C B]$
Da $[A B]$ parallel zu $[E D]$ ist, kann man eine Parallele $i$ , durch den Punkt $D$ konstruieren. Die Gerade $j$ steht senkrecht auf $[A B]$ .
Punkt $E$ ist der Schnittpunkt der Geraden $i$ und $j$ .
$∡ ADC$ = 90°
Winkelhalbierende $[A C [$ halbiert den Winkel $∡ BAD$
Punkt $C$ ist der Schnittpunkt der Winkelhalbierenden und der Halbgeraden $[D C [$ .
Strecke $[C B]$
Begründen Sie, weshalb $∡ E D C = 135 °$ und $A E = E D$ .
Berechnen Sie sodann die Länge der Strecke $[E D]$ .
$[$ Teilergebnis: $E D = 7,78 cm$ $]$
Teilaufgabe b
$∡ E D C = 135 °$ und $[A E] = [E D]$ :
Da $∡ B A E$ = 90° und $[A B]$ parallel zu $[E D]$ ist, ist auch $∡ A E D = 90 °$ .
Da $∡ B A E = 90 °$ und $∡ B A D = 45 °$ ist, ist $∡ D A E = 45$ °.
Innenwinkelsumme im Dreieck $A D E$ : $∡ E D A = 180 ° - 90 ° - 45 ° = 45 °$
$∡ E D C = ∡ A D C + ∡ E D A = 90 ° + 45 ° = 135 °$
$∡ D A E = ∡ E D A = 45 °$
Das rechtwinklige Dreieck $A D E$ hat zwei gleich große Winkel, es ist damit gleichschenklig mit $E D = A E$ .
Länge von $[A E]$ und $[E D]$ :
$\sin (45 °)$ $=$ $\frac{Gegenkathete}{Hypotenuse}$
$\sin (45 °)$ $=$ $\frac{E D}{11 cm}$ $\cdot 11 cm$
$\sin (45 °) \cdot 11 cm$ $=$ $E D$
$E D$ $\approx$ $7,78 c m$
Berechnen Sie die Länge der Strecke $[B C]$ und den prozentualen Anteil des Flächeninhalts des Drachenvierecks $A B C D$ am Flächeninhalt des Fünfecks $A B C D E$ .
$[$ Teilergebnis: $B C = 4,56 cm$ $]$

Teilaufgabe c
Länge von $[B C]$ :
$∡ B A C = 45 ° : 2 = 22,5 °$
( $[A C]$ ist die Symmetrieachse des Drachenvierecks $A B C D$ )
$\tan (22,5 °)$ $=$ $\frac{Gegenkathete}{Ankathete}$
$\tan (22,5 °)$ $=$ $\frac{B C}{11 cm}$ $\cdot 11 c m$
$\tan (22,5 °) \cdot 11 cm$ $=$ $B C$
$B C$ $\approx$ $4,56 cm$
Flächeninhalt des Drachenvierecks $A B C D$ :
Das Viereck $A B C D$ besteht aus zwei flächengleichen rechtwinkligen Dreiecken $A B C$ .
$A_{D}$ $=$ $\frac{1}{2} \cdot B C \cdot A B$
$=$ $\frac{1}{2} \cdot 4,56 cm \cdot 11 cm$
$=$ $25,08 {cm}^{3}$
$A_{F}$ $=$ $A_{D} \cdot 2$
$\approx$ $50,16 {cm}^{3}$
Fläche des Fünfecks $A B C D E$ :
Die Fläche des Fünfecks $A B C D E$ , besteht aus dem Viereck $A B C D$ und dem rechtwinkligen Dreieck $A D E$ .
$A_{D}$ $=$ $\frac{1}{2} \cdot B C \cdot A B$
$=$ $\frac{1}{2} \cdot A E \cdot E D$
$=$ $\frac{1}{2} \cdot 7,78 cm \cdot 7,78 cm$
$\approx$ $30,26 {cm}^{2}$
$A$ $=$ $A_{D} + A_{F}$
$=$ $50,16 {cm}^{2} + 30,26 {cm}^{2}$
$\approx$ $80,42 {cm}^{2}$
Prozentualer Flächenanteil des Drachenvierecks $A B C D$ am Fünfeck $A B C D E$ :
$\frac{50,16 {cm}^{2}}{80,42 {cm}^{2}} \cdot 100 % \approx 62,37 %$
Auf der Strecke $[A E]$ liegen Punkte $S_{n}$ , für die gilt: $E S_{n} (x) = x cm$ mit $x \in ℝ), x \in] 0; 7,78 [$ . Punkte $R_{n}$ liegen auf dem Kreisbogen $\overset{⌢}{A}$ mit dem Mittelpunkt $E$ .
Ferner gilt: $[S_{n} R_{n}] | | [E D]$ .
Zeichnen Sie den Kreisbogen $\overset{⌢}{A}$ und die Strecke $[S_{1} R_{1}]$ für $x = 2$ in die Zeichnung zu Teilaufgabe a) ein.
Teilaufgabe d
Kreisbogen und die Strecke [ $S_{1} R_{1}$ ]:
$[E S_{1}] = 2 cm$
Kreisbogen $b$ von Punkt $A$ bis Punkt $D$ mit Mittelpunkt $E$ und $r = [E D]$ .
$[$ $S_{1} R_{1}$ $[$ ist parallel zu $[E D]$
$R_{1}$ ist der Schnittpunkt von $b$ und der Halbgeraden $[$ $S_{1} R_{1}$ $[$
Der Punkt $R_{2}$ ist der Schnittpunkt des Kreisbogens $\overset{⌢}{A}$ mit der Symmetrieachse $A C$ des Drachenvierecks $A B C D$ .
Ergänzen Sie die Zeichnung zu Teilaufgabe a) um das Dreieck $S_{2} R_{2} E$ und berechnen Sie die Länge der Strecke $[S_{2} R_{2}]$ .
$[$ Zwischenergebnis: $∡ R_{2} A E = ∡ E R_{2} A = 67,5 °]$

Das Dreieck $S_{2} R_{2} E$ :
Länge der Strecke $[S_{2} R_{2}]$ :
Da $[A B] ∥ [E D] ∥ [S_{2} R_{2}]$ und $∡ B A E = 90 °$ , ist auch der Winkel $∡ R_{2} S_{2} E = 90 ° .$ Das heißt, das Dreieck ist rechtwinklig.
Der Winkel $∡ S_{2} E R_{2}$ :
Das Dreieck $A R_{2} E$ ist gleichschenklig, da $[A E] = [R_{2} E]$ . Somit sind auch die Winkel $∡ R_{2} A E = ∡ E R_{2} A$ .
$∡ R_{2} A E$ $=$ $∡ B A E - ∡ B A C$
$=$ $90 ° - 22,5 °$
$=$ $67,5 °$
$=$ $∡ E R_{2} A$
Innenwinkelsumme im Dreieck $A R_{2} E$ :
$∡ A E R_{2}$ $=$ $180 ° - ∡ R_{2} A E - ∡ E R_{2} A$
$=$ $180 ° - 67,5 ° - 67,5 °$
$=$ $45 °$
$\sin (45 °)$ $=$ $\frac{Gegenkathete}{Hypotenuse}$
↓
einsetzen
$\sin (45 °)$ $\approx$ $\frac{R_{2} S_{2}}{E A}$
$\sin (45 °)$ $=$ $\frac{R_{2} S_{2}}{7,78 cm}$ $\cdot 7,78 cm$
$R_{2} S_{2}$ $=$ $\sin (45 °) \cdot 7,78 cm$
$\approx$ $5,50 cm$
Die Bogenlänge $b$ des Kreisbogens $\overset{⌢}{R_{3}}$ mit dem Mittelpunkt $E$ beträgt $3 cm$ . Berechnen Sie das Maß des Winkels $R_{3} E D$ und den zugehörigen Wert für $x$ .

Teilaufgabe f
$∡ R_{3} E D$ mit Bogenlänge $b = 3 cm$ , Mittelpunkt $E$ :
Bogenlänge allgemein: $b = U \cdot \frac{α}{360^{\circ}} = 2 \cdot r \cdot π \cdot \frac{α}{360^{\circ}}$
Bekannte Werte einsetzen:
↓
$3$ $=$ $2 \cdot 7,78 \cdot π \cdot \frac{α}{360^{\circ}}$ $360^{\circ}$
$1080^{\circ}$ $=$ $15,56 \cdot π \cdot α$ $: (15,56 \cdot π)$
$α$ $\approx$ ${22,09}^{\circ}$
Der zugehörige Wert $x = [E S_{3}]$ :
$∡ S_{3} E R_{3} = 90 ° - α$
$∡ S_{3} E R_{3}$ $=$ $90 ° - α$
$\approx$ $90 ° - 22,09 °$
$\approx$ $67,91 °$
$\cos (67,91 °)$ $=$ $\frac{Ankathete}{Hypotenuse}$
$\cos (67,91 °)$ $=$ $\frac{x}{7,78}$ $\cdot 7,78$
$x$ $=$ $\cos (67,91 °) \cdot 7,78$
$x$ $=$ $2,93$

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org

$\sin (45 °)$	$=$	$\frac{Gegenkathete}{Hypotenuse}$
$\sin (45 °)$	$=$	$\frac{E D}{11 cm}$	$\cdot 11 cm$
$\sin (45 °) \cdot 11 cm$	$=$	$E D$
$E D$	$\approx$	$7,78 c m$

$\tan (22,5 °)$	$=$	$\frac{Gegenkathete}{Ankathete}$
$\tan (22,5 °)$	$=$	$\frac{B C}{11 cm}$	$\cdot 11 c m$
$\tan (22,5 °) \cdot 11 cm$	$=$	$B C$
$B C$	$\approx$	$4,56 cm$

$A_{D}$	$=$	$\frac{1}{2} \cdot B C \cdot A B$
	$=$	$\frac{1}{2} \cdot 4,56 cm \cdot 11 cm$
	$=$	$25,08 {cm}^{3}$

$A_{D}$	$=$	$\frac{1}{2} \cdot B C \cdot A B$
	$=$	$\frac{1}{2} \cdot A E \cdot E D$
	$=$	$\frac{1}{2} \cdot 7,78 cm \cdot 7,78 cm$
	$\approx$	$30,26 {cm}^{2}$

$A$	$=$	$A_{D} + A_{F}$
	$=$	$50,16 {cm}^{2} + 30,26 {cm}^{2}$
	$\approx$	$80,42 {cm}^{2}$

$∡ R_{2} A E$	$=$	$∡ B A E - ∡ B A C$
	$=$	$90 ° - 22,5 °$
	$=$	$67,5 °$
	$=$	$∡ E R_{2} A$

$∡ A E R_{2}$	$=$	$180 ° - ∡ R_{2} A E - ∡ E R_{2} A$
	$=$	$180 ° - 67,5 ° - 67,5 °$
	$=$	$45 °$

$\sin (45 °)$	$=$	$\frac{Gegenkathete}{Hypotenuse}$
	↓	einsetzen
$\sin (45 °)$	$\approx$	$\frac{R_{2} S_{2}}{E A}$
$\sin (45 °)$	$=$	$\frac{R_{2} S_{2}}{7,78 cm}$	$\cdot 7,78 cm$
$R_{2} S_{2}$	$=$	$\sin (45 °) \cdot 7,78 cm$
	$\approx$	$5,50 cm$

Bekannte Werte einsetzen:
	↓
$3$	$=$	$2 \cdot 7,78 \cdot π \cdot \frac{α}{360^{\circ}}$	$360^{\circ}$
$1080^{\circ}$	$=$	$15,56 \cdot π \cdot α$	$: (15,56 \cdot π)$
$α$	$\approx$	${22,09}^{\circ}$

$∡ S_{3} E R_{3}$	$=$	$90 ° - α$
	$\approx$	$90 ° - 22,09 °$
	$\approx$	$67,91 °$

$\cos (67,91 °)$	$=$	$\frac{Ankathete}{Hypotenuse}$
$\cos (67,91 °)$	$=$	$\frac{x}{7,78}$	$\cdot 7,78$
$x$	$=$	$\cos (67,91 °) \cdot 7,78$
$x$	$=$	$2,93$

Teil B

Teilaufgabe a

Teilaufgabe b

Teilaufgabe c

Teilaufgabe d

Teilaufgabe f