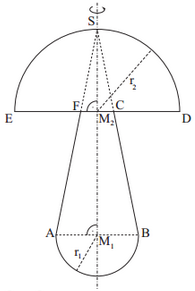
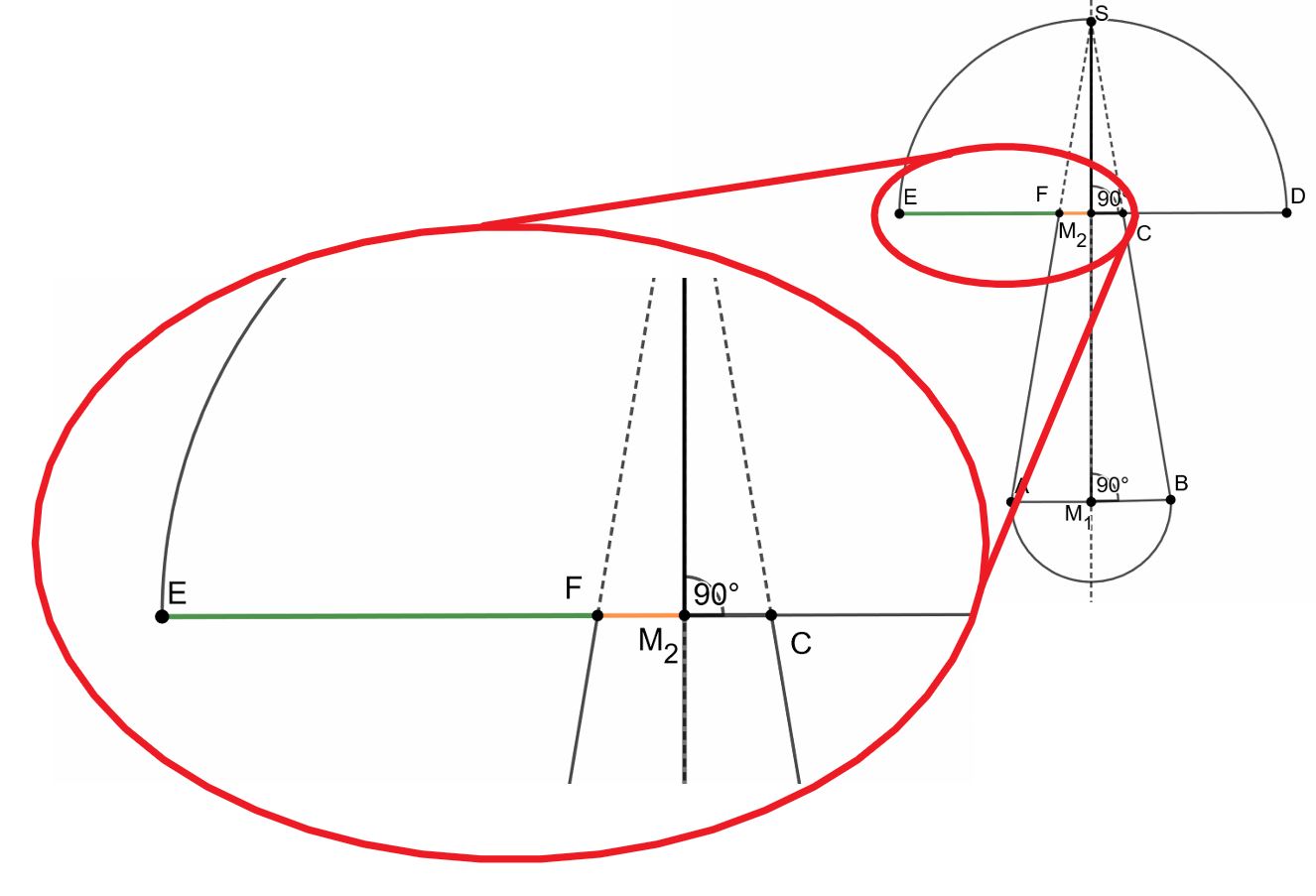
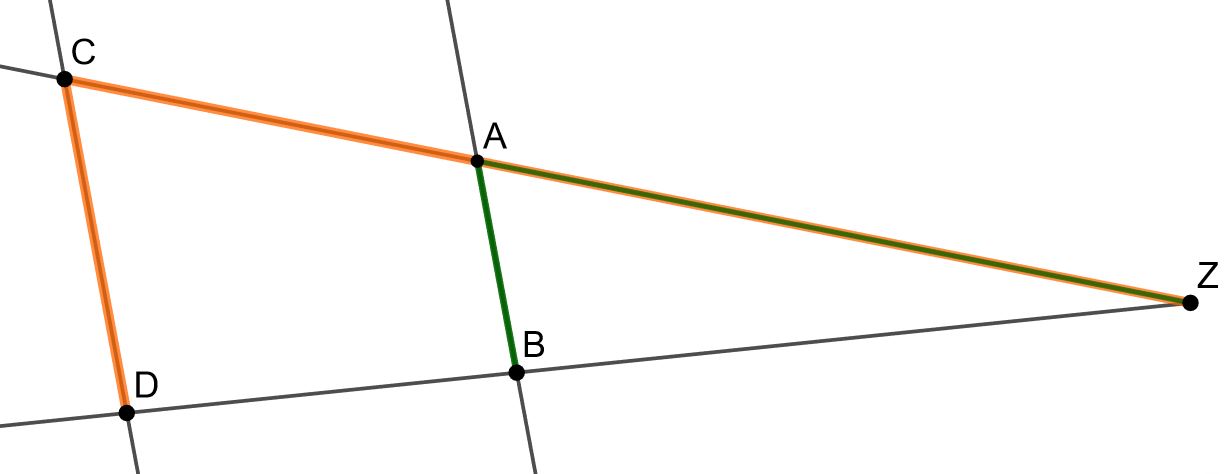
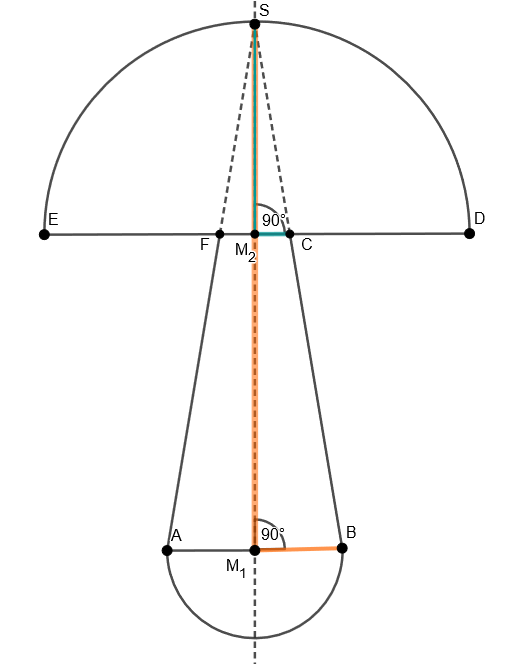
Oberflächeninhalt der kleineren Halbkugel
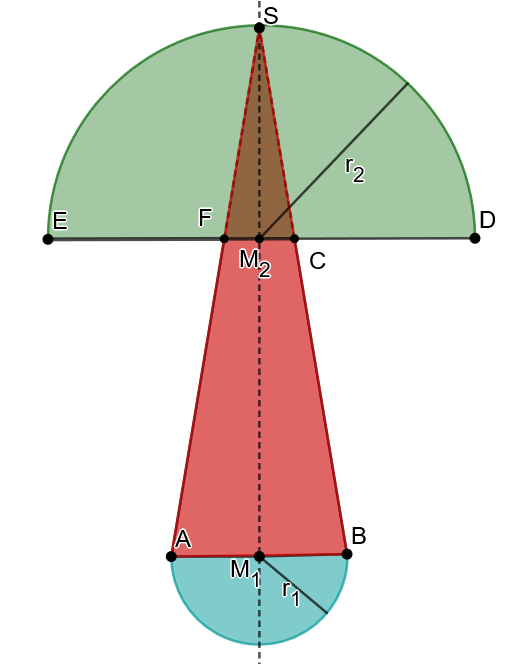
Im ersten Schritt berechnest du den Oberflächeninhalt der türkisen, kleineren Halbkugel.
Den Oberflächeninhalt einer Kugel berechnet man durch folgende Formel.
Die Kugel hat den Radius . Da du nur eine Halbkugel vorliegen hast, halbierst du den Oberflächeninhalt noch:
| | | |
| ↓ | Setze den Radius ein. |
| | | |
| ↓ | Vereinfache so weit wie möglich. |
| | | |
| ↓ | Berechne und Runde. |
| | | |
Der Oberflächeninhalt der kleinen, türkisen Halbkugel beträgt gerundet .
Oberflächeninhalt der größeren Halbkugel
Nun berechnest du den Oberflächeninhalt der größeren, grünen Halbkugel. Für diese Berechnung bestimmst du die Hälfte des Oberflächeninhalts einer ganzen Kugel mit Radius .
| | | |
| ↓ | Setze die Formel zur Bestimmung des Oberflächeninhaltes der Kugel ein und halbiere ihn. |
| | | |
| ↓ | Setze den Radius ein. |
| | | |
| ↓ | Vereinfache soweit wie möglich. |
| | | |
| ↓ | Berechne und Runde das Ergebnis |
| | | |
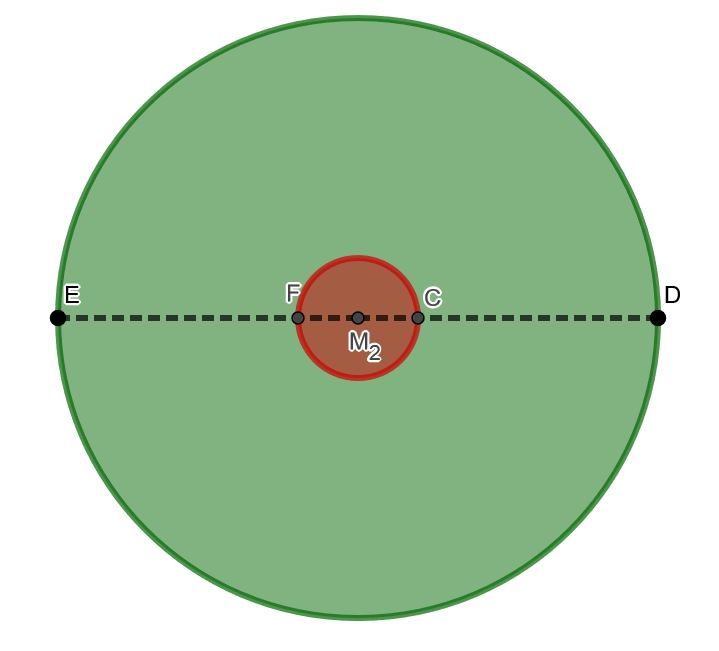
Flächeninhalt des Kreisrings
Um den Flächeninhalt des Kreisrings zu bestimmen, subtrahierst du den Flächeninhalt des Kreises mit Radius von dem Flächeninhalt des Kreises mit Radius .
| | | |
| ↓ | Setze die beiden Radien ein. |
| | | |
| ↓ | Vereinfache so weit wie möglich. |
| | | |
| ↓ | Vereinfache weiter. |
| | | |
| ↓ | Berechne und runde auf eine Nachkommastelle. |
| | | |
Der Flächeninhalt des Kreisrings beträgt circa .
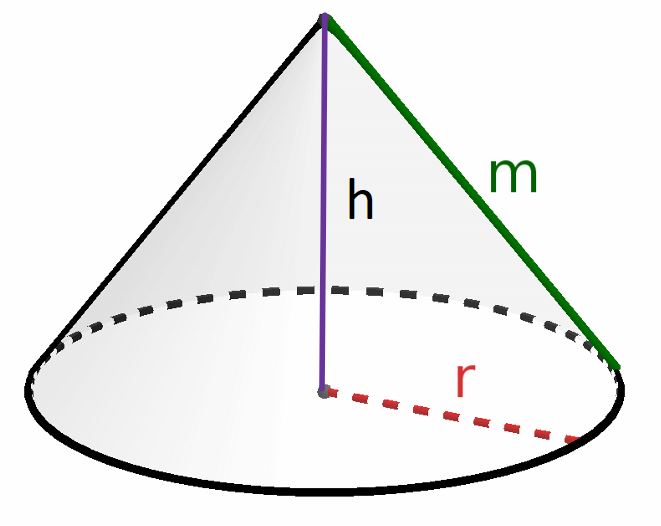
Oberflächeninhalt des Kegels
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
| | | |
Der Oberflächeninhalt des Kegelstumpfes beträgt gerundet .
Oberflächeninhalt des gesamten Rotationskörpers
Für den Oberflächeninhalt des gesamten Rotationskörper sind lediglich die äußeren Oberflächenstücke entscheidend.
Deshalb addiert man für die Gesamtoberfläche den Oberflächeninhalt der großen Halbkugel, den Flächeninhalt des Kreisrings, den Oberflächeninhalt des Kegelstumpfs und den Oberflächeninhalt der kleineren Halbkugel.
Der Oberflächeninhalt umfasst also .