Gemischte Aufgaben zu Geraden, Strecken oder Halbgeraden

Hier findest du Übungsaufgaben zu Geraden, Strecken und Halbgeraden. Wiederhole wichtige Grundlagen und vertiefe dein Wissen!

1
Bestimme die größte Anzahl von Schnittpunkten, die $2, 3, \dots, n$ Geraden bilden können.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schnittpunkt zweier Funktionen
Zwei nicht parallele Geraden $f$ und $g$ haben einen Schnittpunkt. (Bild oben links)
$N_{2} = 1$
Eine weitere Gerade $h$ kann (sofern sie nicht parallel zu $f$ oder $g$ ist) $f$ und $g$ schneiden. Zu dem einen Schnittpunkt $S 1$ kommen $2$ Schnittpunkte dazu $S 2$ und $S 3$ .
$3$ Geraden können $3$ Schnittpunkte haben. (Bild oben rechts)
$N_{3} = 1 + 2 = 3$
Eine weitere Gerade $i$ kann (sofern sie nicht parallel zu einer der vorherigen Geraden ist) $f$ , $g$ und $h$ schneiden. Zu den $3$ Schnittpunkten kommen $3$ Schnittpunkte hinzu $S 4$ , $S 5$ und $S 6$ .
$4$ Geraden können $6$ Schnittpunkte haben. (Bild unten links)
$N_{4} = 1 + 2 + 3 = 6$
Eine weitere Gerade $j$ kann (sofern sie nicht parallel zu einer der vorherigen Geraden ist) $f$ , $g$ , $h$ und $i$ schneiden. Zu den $6$ Schnittpunkten kommen $4$ Schnittpunkte hinzu $S 7$ , $S 8$ , $S 9$ und $S 10$ .
$5$ Geraden können $10$ Schnittpunkte haben. (Bild unten rechts)
$N_{5} = 1 + 2 + 3 + 4 = 10$
.
.
.
$N_{n} = 1 + 2 + 3 + 4 + 5 + 6 + 7 + . . . . . + (n - 1)$
Für diese Summe gibt es eine Formel, die Gaußsche Summenformel:
$\sum_{n = 0}^{n} k = \frac{(n) \cdot (n + 1)}{2}$
Bei den Geradenschnittpunkten beginnt die Summe bei $n = 1$ und geht bis $(n - 1)$ . Für insgesamt $n$ Geraden kann die maximale Anzahl der Schnittpunkte dann nach folgender Formel berechnet werden:
$N_{n} = \sum_{k = 1}^{n - 1} k = \frac{(n - 1) \cdot n}{2}$
Probe:
$n = 4 \Rightarrow N = \sum_{n = 1}^{3} k = \frac{(4 - 1) \cdot 4}{2} = \frac{3 \cdot 4}{2} = 6$
$n = 5 \Rightarrow N = \sum_{n = 1}^{4} k = \frac{(5 - 1) \cdot 5}{2} = \frac{4 \cdot 5}{2} = 10$
2
Zeichne ein Gitternetz und trage die Punkte $A (3 | 3)$ , $B (7 | 6)$ , $C (3 | 9)$ und $D (2 | 5)$ ein.
Zeichne $A B$ , $[C B$ und $[A D]$ ein.
Fälle von $C$ das Lot auf $A D$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade, Strecken, Halbgeraden
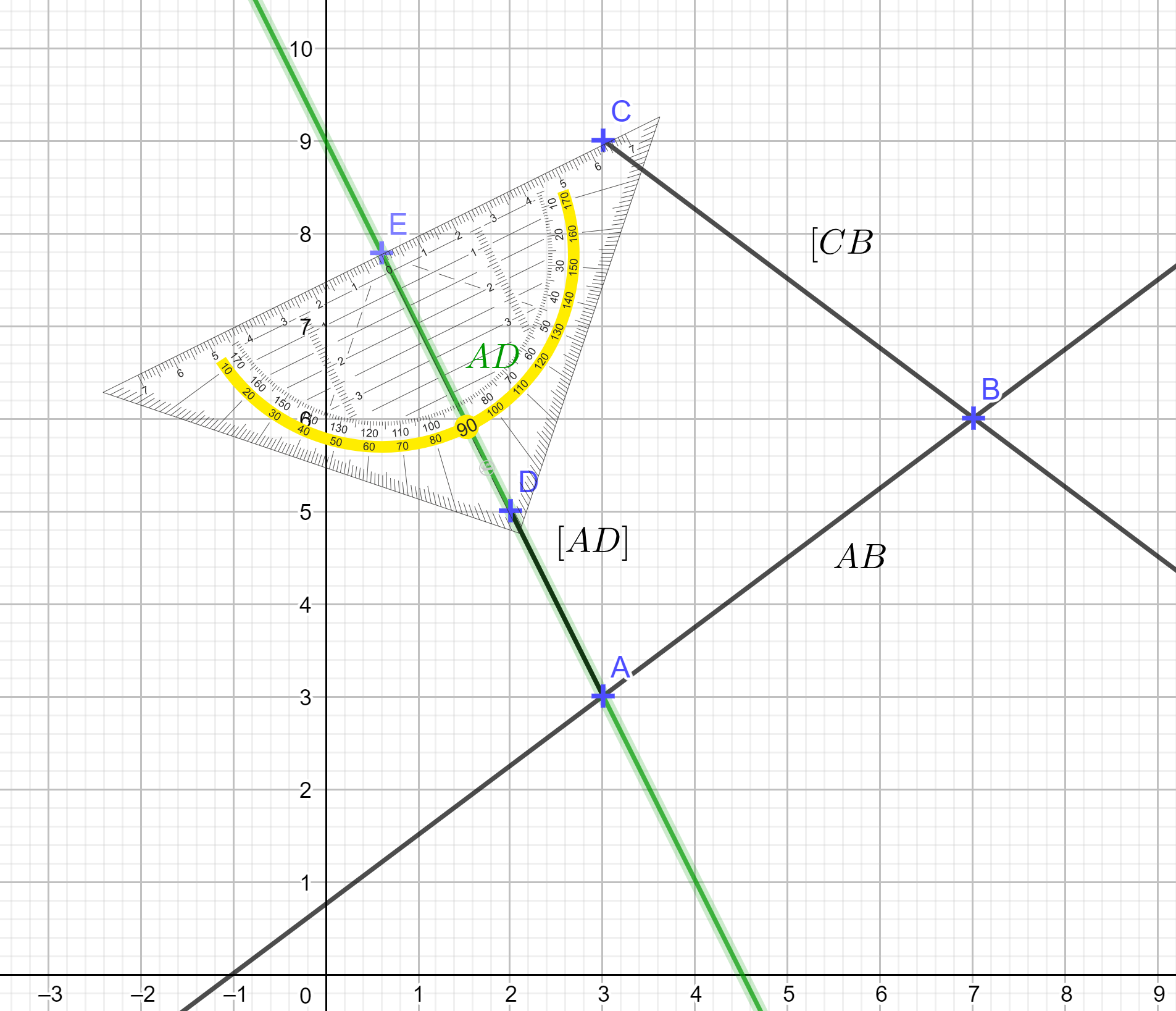
$A B$ ist die Gerade durch die Punkte $A$ und $B$ .
$[C B$ ist die Halbgerade (oder der Strahl) von $C$ durch $B$ .
$[A D]$ ist die Strecke zwischen $A$ und $D$ .
$A D$ ist die Gerade durch $A$ und $D$ (in grün).
$E$ ist der Fusspunkt des Lots von $C$ auf die Gerade $A D$ , der mit einem Geodreieck eingezeichnet wurde.
3
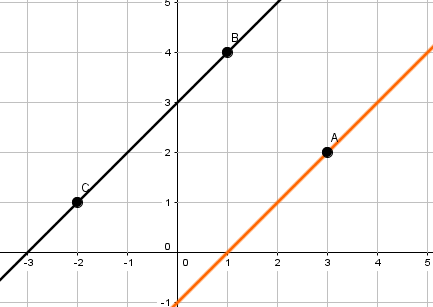
Zeichne die Gerade $A B$ und den Punkt $C$ in ein Koordinatensystem ein und miss den Abstand mit einem Geodreieck.
$A (2 | 2)$ , $B (4 | 6)$ , $C (6 | 3)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
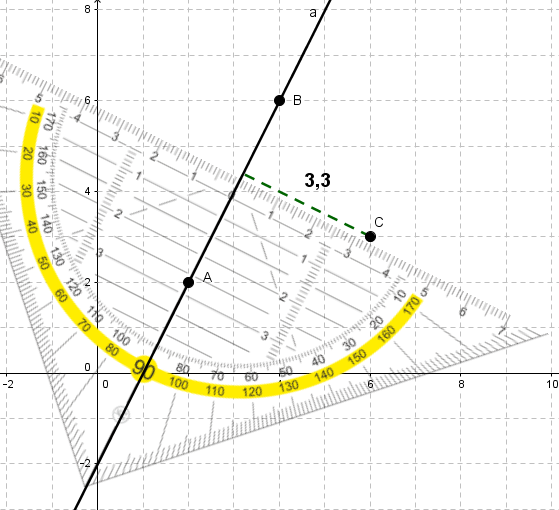
Trage alle Punkte ins Koordinatensystem ein und verbinde die Punkte A und B zu einer Gerade.
Lege die Mittellinie des Geodreiecks auf die Gerade und schiebe es solange nach oben/unten bis du den Punkt C erreichst.
Lies den Abstand ab.
Abstand: 3,1cm - 3,5cm (wird als Lösung akzeptiert: Zeichenungenauigkeit)

$A (2 | 2)$ , $B (4 | 6)$ , $C (1 | 5)$

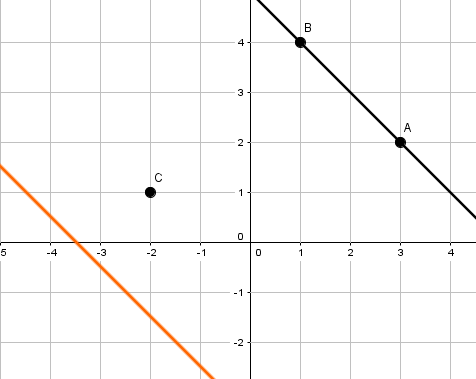
Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
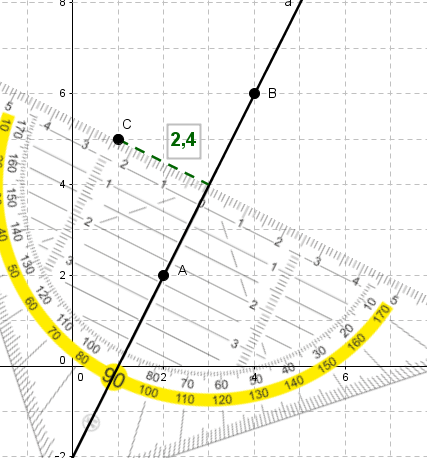
Trage alle Punkte ins Koordinatensystem ein und verbinde die Punkte A und B zu einer Gerade.
Lege die Mittellinie des Geodreiecks auf die Gerade und schiebe es solange nach oben/unten bis du den Punkt C erreichst.
Lies den Abstand ab.
Abstand: 2,2cm - 2,6cm (wird als Lösung akzeptiert: Zeichenungenauigkeit)

$A (6 | 1)$ , $B (2 | 5)$ , $C (7 | 6)$

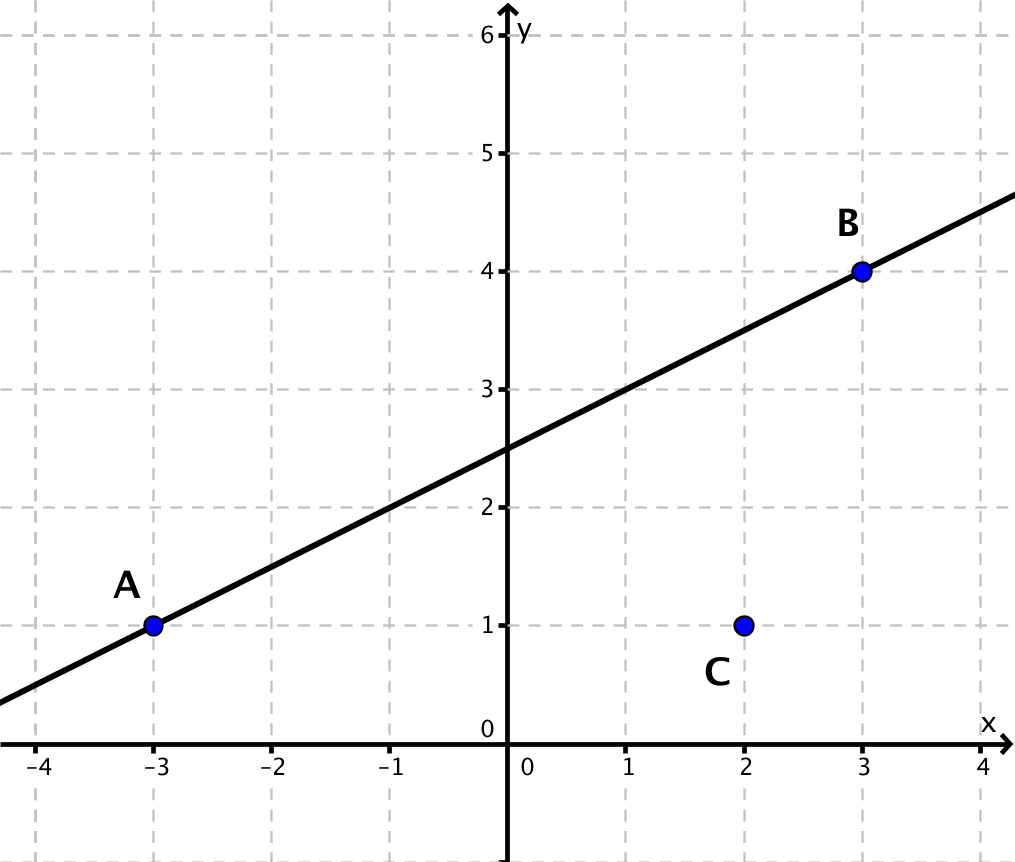
Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
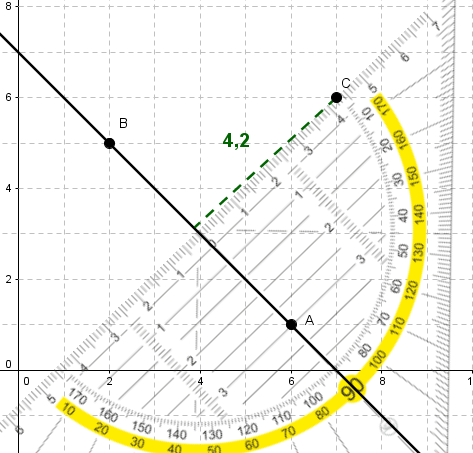
Trage alle Punkte ins Koordinatensystem ein und verbinde die Punkte A und B zu einer Gerade.
Lege die Mittellinie des Geodreiecks auf die Gerade und schiebe es solange nach oben/unten bis du den Punkt C erreichst.
Lies den Abstand ab.
Abstand: 4,0cm - 4,4cm (wird als Lösung akzeptiert: Zeichenungenauigkeit)
4
Löse die folgenden Aufgaben
Zeichne ein Gitternetz und trage die Punkte $A (3 | 2)$ , $B (1 | 4)$ und $C (- 2 | 1)$ ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Senkrechte Gerade
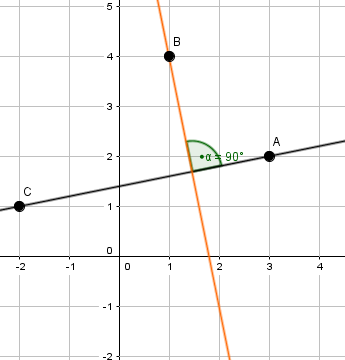
Trage die Punkte $A$ , $B$ und $C$ in das Koordinatensystem ein.

Fälle von $B$ das Lot auf $A C$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Senkrechte Gerade
Zeichne die Gerade $A C$ ein.
Fälle das Lot durch $B$ auf die Gerade $A C$ .

Zeichne die Parallele zu $B C$ durch $A$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallele Gerade durch Punkt
Zeichne die Gerade $B C$ ein.
Lege das Geodreieck an die Gerade $B C$ an und verschiebe es, bis du den Punkt $A$ erreicht hast.
Zeichne die Gerade ein.

Zeichne eine Parallele zu $A B$ im Abstand $6 c m$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallele mit gewissen Abstand zeichnen
Zeichne die Gerade $A B$ ein.
Lege das Geodreieck an der Geraden $A B$ an und verschiebe es so lange bis du den gewünschten Abstand (Innenskala) erreicht hast.
Zeichne die parallele Gerade ein.
5
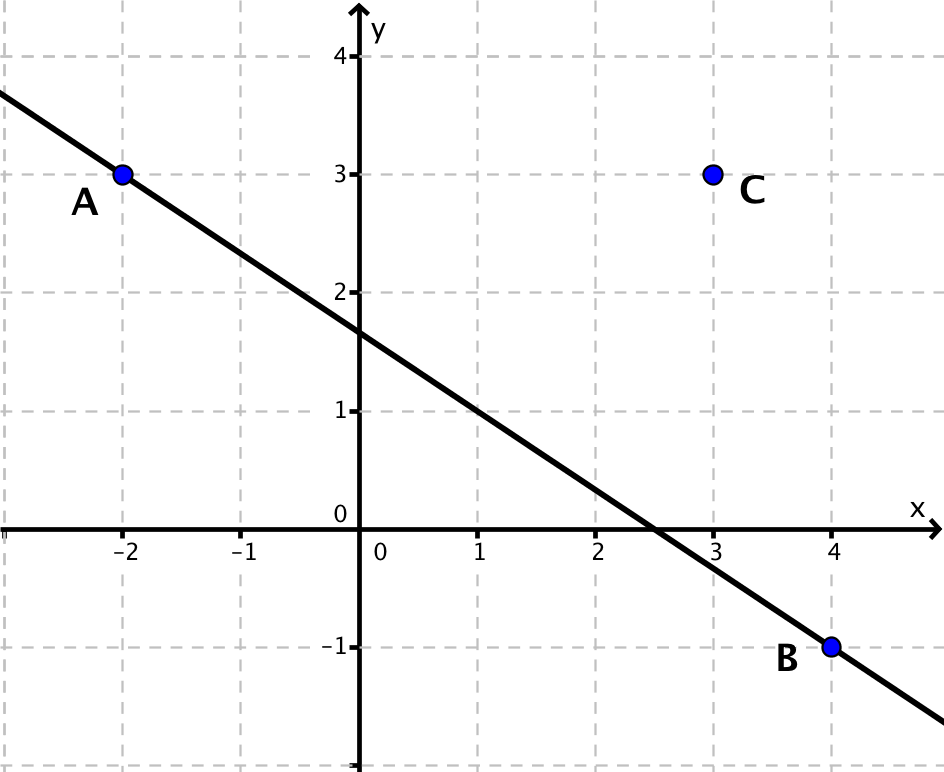
Bestimme den Abstand der Gerade $A B$ zu dem Punkt $C$ .
$A (- 3 | 1), B (3 | 4), C (2 | 1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand eines Punktes zu einer Geraden
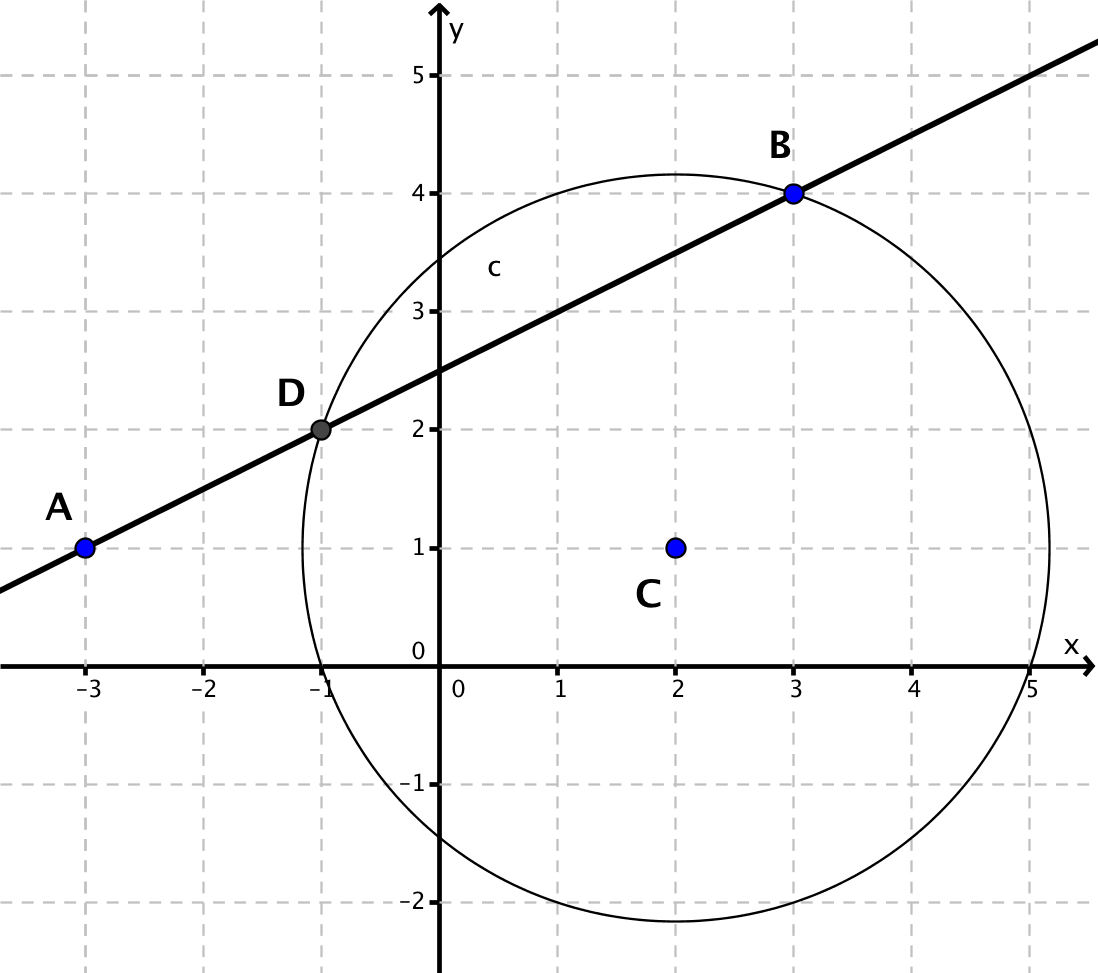
Zeichne die Gerade AB und den Punkt C in ein Koordinatensystem ein.
Zeichne einen Kreis mit dem Mittelpunkt C, der die Gerade AB in zwei Punkten schneidet. Für den Radius des Kreises gibt es viele Möglichkeiten.
Der hier gewählte Kreis schneidet die Gerade AB in den Punkten B und D. Konstruiere nun die Mittelsenkrechte zu den Punkten D und B und bestimme den Schnittpunkt der Mittelsenkrechten mit der Geraden AB.
Die Mittelsenkrechte wurde hier orange eingezeichnet und der Schnittpunkt mit der Geraden AB mit E bezeichnet. Die Mittelsenkrechte steht senkrecht auf der Geraden AB und verläuft durch den Punkt C. Die Strecke [EC] ist also die kürzeste Verbindung von dem Punkt C zu der Geraden AB. Der Abstand von C zu AB entspricht also der Länge der Strecke [EC].
Miss nun die Länge der Strecke [EC]
$EC \approx 2,2$
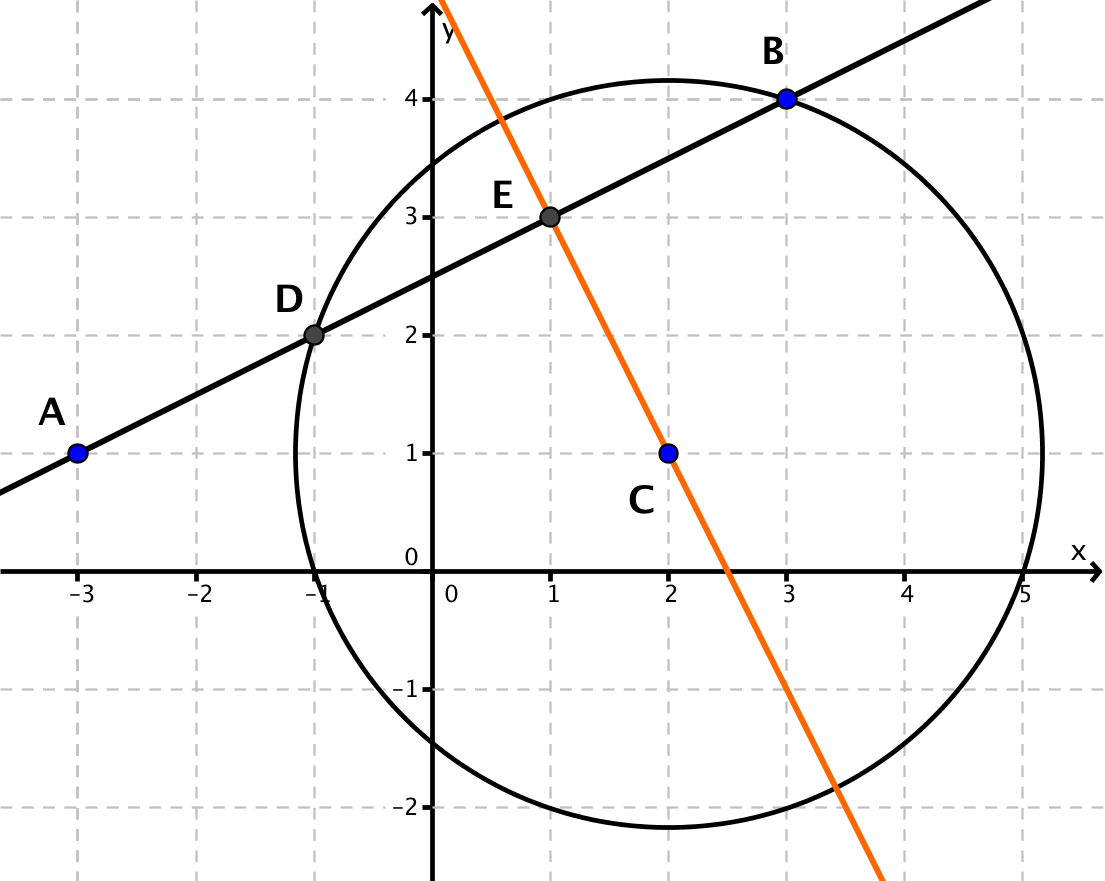
Antwort: Der Abstand des Punktes C zur Gerade AB beträgt ca. 2,2.

$A (- 3 | 1), B (3 | 4), C (- 2 | 5)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand eines Punktes zu einer Geraden
Zeichne die Gerade AB und den Punkt C in ein Koordinatensystem ein.
Zeichne einen Kreis mit dem Mittelpunkt C, der die Gerade AB in zwei Punkten schneidet. Für den Radius des Kreises gibt es viele Möglichkeiten.
Der hier gewählte Kreis schneidet die Gerade AB in den Punkten B und D. Konstruiere nun die Mittelsenkrechte zu den Punkten D und B und bestimme den Schnittpunkt der Mittelsenkrechten mit der Geraden AB.
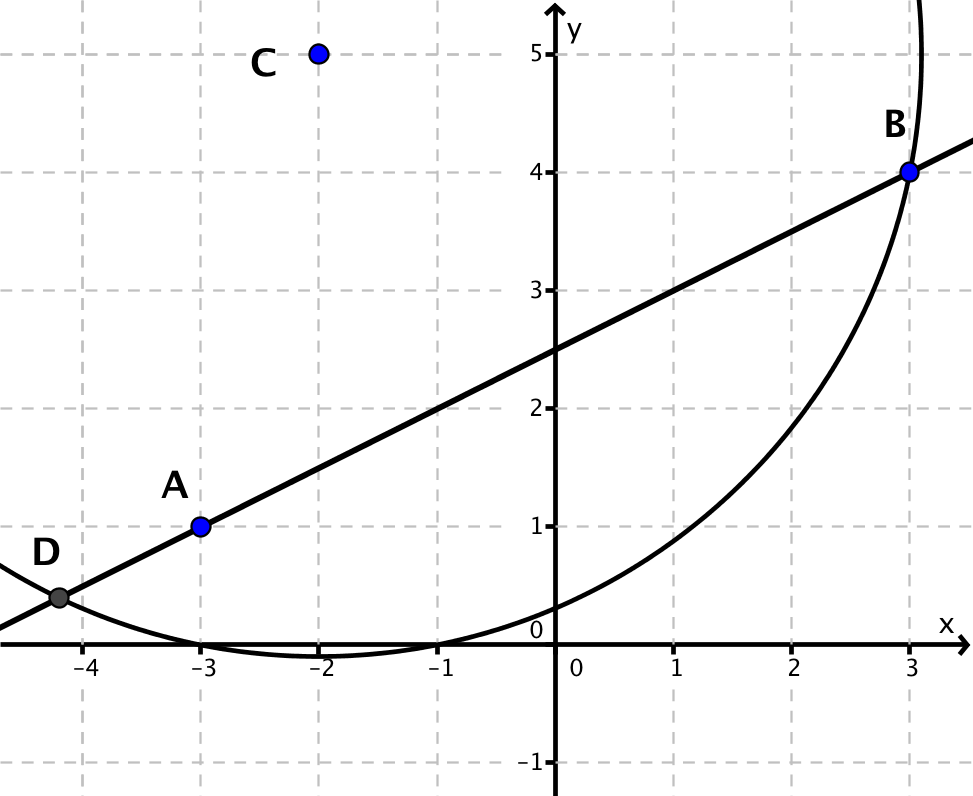
Die Mittelsenkrechte wurde hier orange eingezeichnet und der Schnittpunkt mit der Geraden AB mit E bezeichnet. Die Mittelsenkrechte steht senkrecht auf der Geraden AB und verläuft durch den Punkt C. Die Strecke [EC] ist also die kürzeste Verbindung von dem Punkt C zu der Geraden AB. Der Abstand von C zu AB entspricht also der Länge der Strecke [EC].
Miss nun die Länge der Strecke [EC]
$EC \approx 3,1$
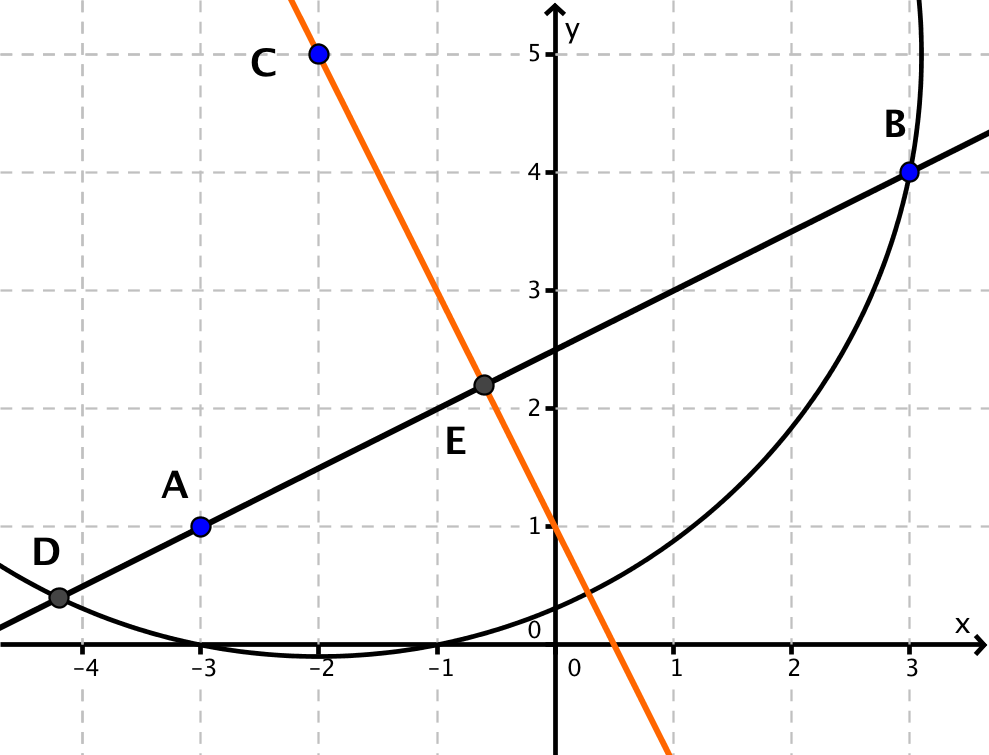
Antwort: Der Abstand des Punktes C zur Gerade AB beträgt ca. 3,1.

$A (- 2 | 3), B (4 | - 1), C (3 | 3)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand eines Punktes zu einer Geraden
Zeichne die Gerade AB und den Punkt C in ein Koordinatensystem ein.
Zeichne einen Kreis mit dem Mittelpunkt C, der die Gerade AB in zwei Punkten schneidet. Für die Wahl des Radius des Kreises gibt es viele Möglichkeiten.
Der hier gewählte Kreis schneidet die Gerade AB in den Punkten B und D. Konstruiere nun die Mittelsenkrechte zu den Punkten D und B und bestimme den Schnittpunkt der Mittelsenkrechten mit der Geraden AB.
Die Mittelsenkrechte wurde hier orange eingezeichnet und der Schnittpunkt mit der Geraden AB mit E bezeichnet. Die Mittelsenkrechte steht senkrecht auf der Geraden AB und verläuft durch den Punkt C. Die Strecke [EC] ist also die kürzeste Verbindung von dem Punkt C zu der Geraden AB. Der Abstand von C zu AB entspricht also der Länge der Strecke [EC].
Miss nun die Länge der Strecke [EC]
$EC \approx 2,8$
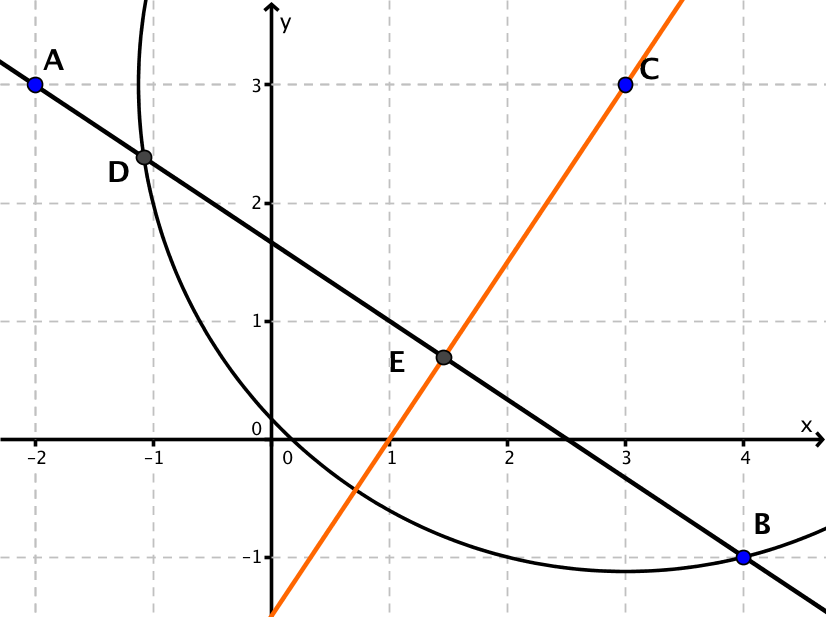
Antwort: Der Abstand des Punktes C zur Gerade AB beträgt ca. 2,8.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org