Nullstellenberechnung

1 Übersicht

Nullstellen und deren Berechnung sind in vielen Bereichen der Mathematik und anderen Wissenschaften von Bedeutung. In diesem Kurs lernst du, welche Strategien du anwenden kannst, um Nullstellen ausgewählter Funktionen bestimmen zu können.

Vorkenntnisse

Umformen von Gleichungen
Graphen zeichnen und auswerten
Grundkenntnisse über die verschiedenen Funktionstypen

Kursdauer:

ca. 3 Stunden

2 Definition von Nullstellen

Eine Nullstelle einer Funktion $f$ ist der $x$ -Wert eines Schnittpunktes vom Graphen von $f$ mit der x-Achse.

Das sind also gerade die $x$ -Werte, an denen $f (x) = 0$ ist.

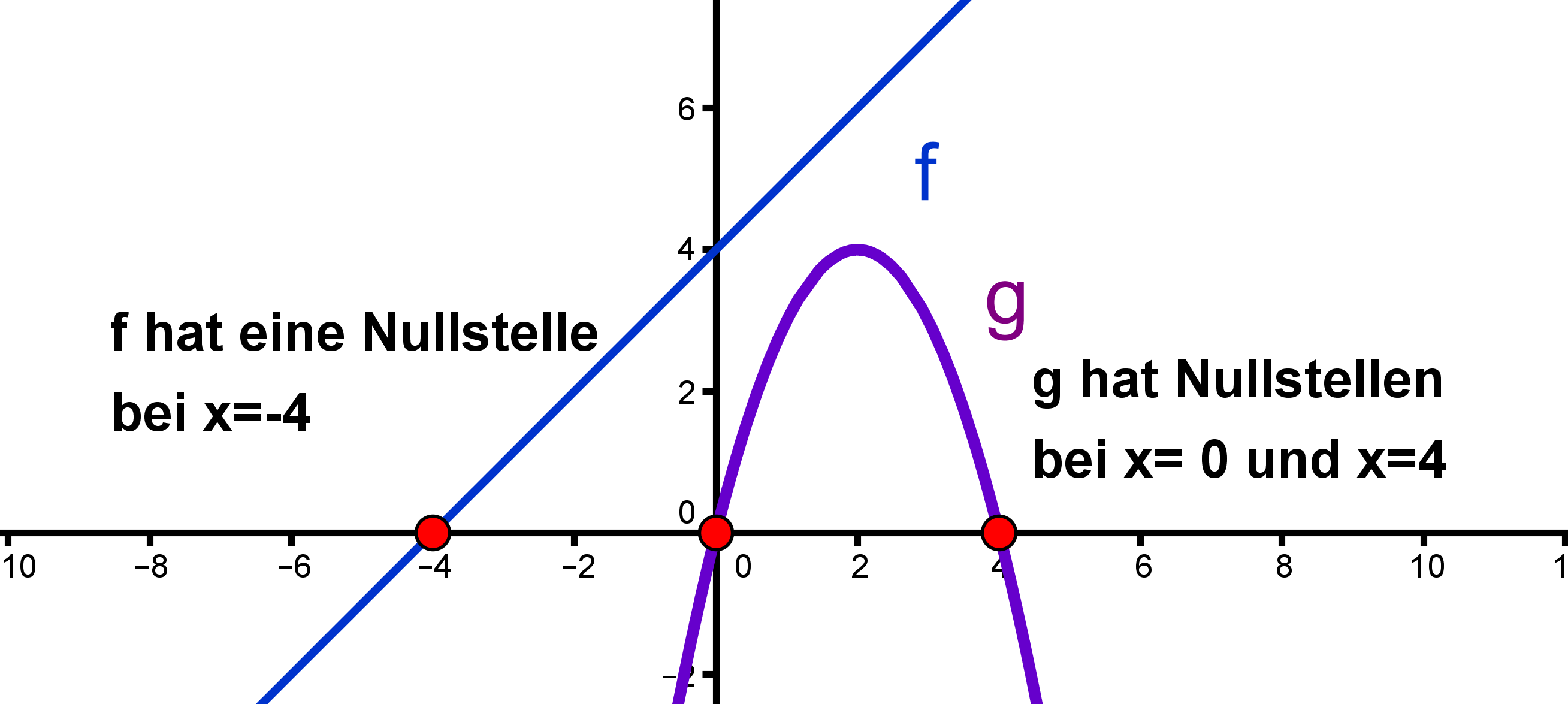
Hier sind die Nullstelle(n) der linearen Funktion f mit $f (x) = x + 4$ und der quadratischen Funktion g mit $g (x) = - (x - 2)^{2} + 4$ eingezeichnet.

Zur Berechnung der Nullstellen einer Funktion, brauchst du also Folgendes immer zu beachten:

Die Nullstellen einer Funktion $f$ sind die $x$ -Werte, für die $f (x) = 0$ wird.

3 Vorgehen bei der Nullstellenbestimmung

Wie du bei der Nullstellenberechnung vorgehst, hängt davon ab, welcher Funktionstyp vorliegt.

Handelt es sich um …

4 Nullstellen von ganzrationalen Funktionen

Eine ganzrationale Funktion ist eine Funktion der Form $f (x) = a_{n} \cdot x^{n} + a_{n - 1} \cdot x^{n - 1} + \dots + a_{2} \cdot x^{2} + a_{1} \cdot x + a_{0}$

Beispiele sind die Funktionen $g (x) = 3 x^{2} + 2$ oder $h (x) = 7 x^{6} + x^{4} - 9$ .

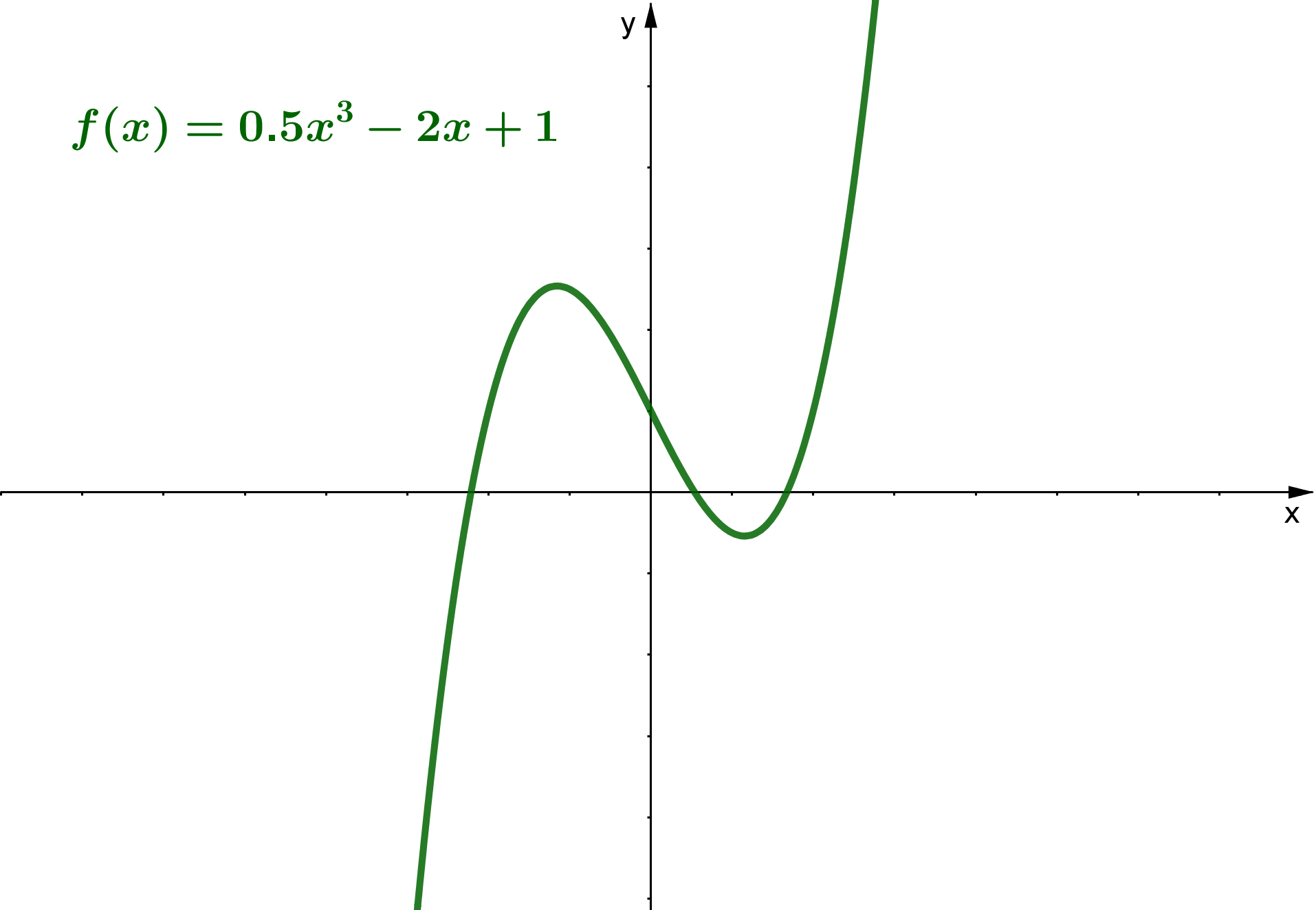
Wie du die Nullstellen einer Polynomfunktion berechnen kannst, hängt von der Form und vom Grad der Funktion ab.

Ist die Funktion in Linearfaktordarstellung, kannst du die Nullstellen sofort ablesen. Du musst nur betrachten, für welche Zahlen die einzelnen Faktoren Null werden.

Ist nur ein Teil der Funktion in Linearfaktoren zerlegt, musst du die Nullstellen der einzelnen Faktoren teilweise mit anderen Mitteln bestimmen wie z.B. der quadratischen Lösungsformel.

Handelt es sich um eine Summe aus einer Potenzfunktion und einer Konstanten, dann bringe die Konstante auf die andere Seite des Gleichheitszeichens und ziehe die Wurzel.

Bei einer quadratische Funktion kannst du die Nullstellen mithilfe der quadratischen Lösungsformel oder mit dem Satz von Vieta bestimmen.

Handelt es sich um eine Polynomfunktion vom Grad $n > 2$ , gibt es unterschiedliche Vorgehensweisen bei der Nullstellenbestimmung:
- kleinste Potenz von $x$ ausklammern
- Substitution
- Polynomdivision

Eine ausführliche Erklärung zur Nullstellenberechnung bei ganzrationalen Funktionen findest du in dem Kurs: Berechnungsmethoden - Nullstellen von Polynomfunktionen.

5 Nullstellen von gebrochenrationalen Funktionen

Eine gebrochenrationale Funktion ist eine Funktion, die sich als Bruch von Polynomen darstellen lässt. Gebrochenrationale Funktionen sind also von der Form $f (x) = \frac{p (x)}{q (x)}$ , wobei sowohl $p (x)$ als auch $q (x)$ Polynome sind.

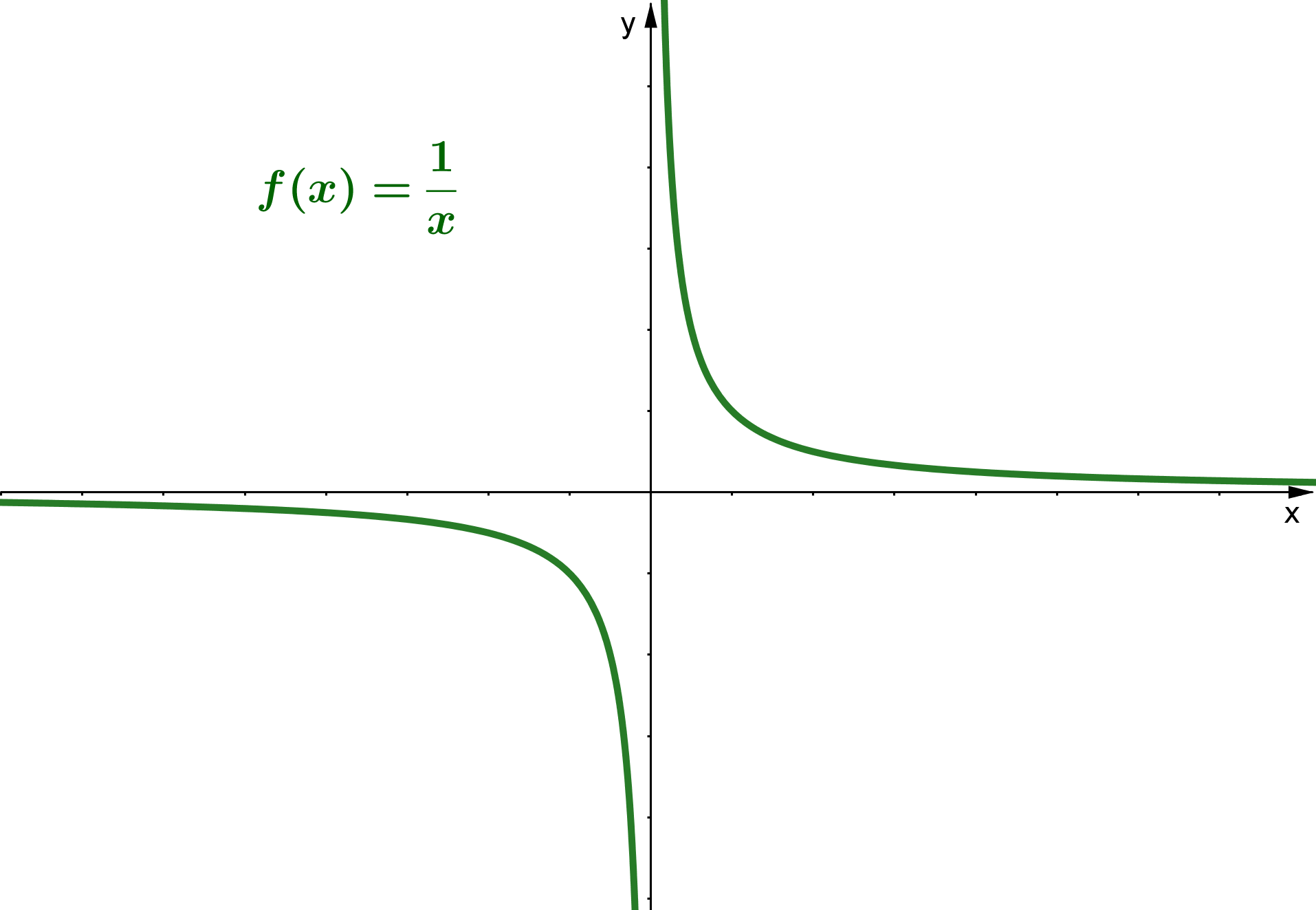
Eine gebrochenrationale Funktion wird genau dann Null, wenn das Zählerpolynom $p (x) = 0$ ist und das Nennerpolynom an der ermittelten Nullstelle $q (x) \neq 0$ ist.

Beispiel

$f (x) = \frac{p (x)}{q (x)} = \frac{x^{2} - 4 x + 3}{x^{2} - 1}$

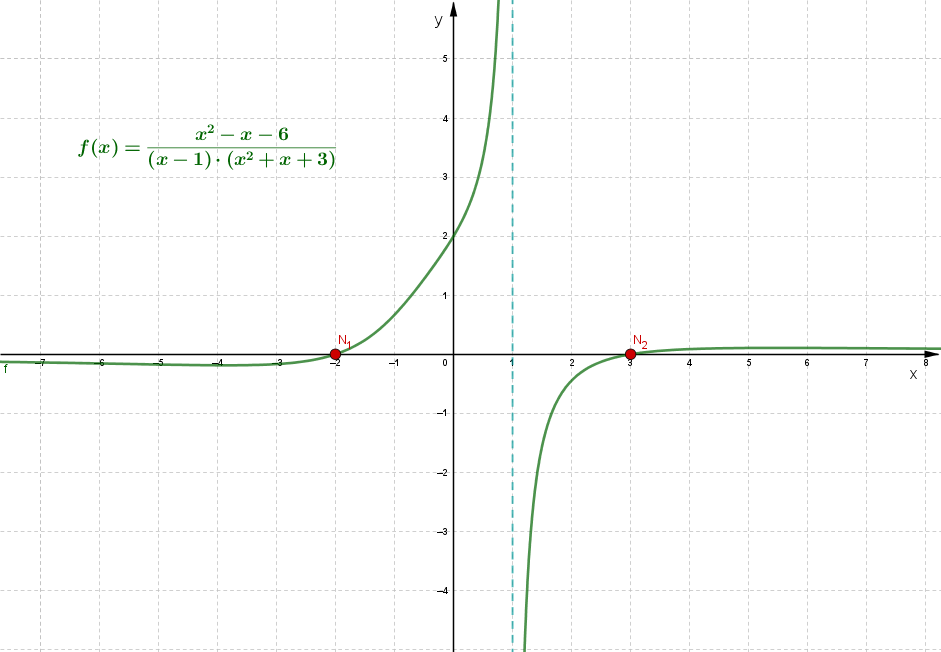
Sowohl das Zählerpolynom als auch das Nennerpolynom hat eine Nullstelle unter anderem bei $x_{0} = 1$ . An dieser Stelle nimmt die gebrochenrationale Funktion den Wert $f (x_{0}) = - 1$ an.

Berechnung der Nullstellen

Um die Nullstellen von $f (x)$ zu berechnen, brauchst du also nur das Polynom $p (x) = 0$ zu setzen. Du musst aber danach prüfen, dass für das Nennerpolynom an der ermittelten Nullstelle $q (x) \neq 0$ gilt. Die Nullstellen von $p (x)$ kannst du auf die gleiche Weise bestimmen, wie es auf der Kursseite Nullstellen von ganzrationalen Funktionen beschrieben wird.

Dabei muss eine beliebige Nullstellen $x_{0}$ auch im Definitionsbereich der Funktion liegen, also $x_{0} \in 𝔻_{f}$ .

Beispiel

$f (x) = \frac{p (x)}{q (x)}$	$=$	$\frac{x^{2} - x - 6}{(x - 1) (x^{2} + x + 3)} = 0$
	↓	Berechne die möglichen Nullstellen von $f (x)$ . Setze dazu $p (x) = 0$ .
$p (x)$	$=$	$x^{2} - x - 6 = 0$
	↓	Mitternachtsformel anwenden.
$x_{1,2}$	$=$	$\frac{1 \pm \sqrt{(- 1)^{2} - 4 \cdot 1 \cdot (- 6)}}{2 \cdot 1}$
	$=$	$\frac{1 \pm \sqrt{25}}{2} = \frac{1 \pm 5}{2}$
$x_{1}$	$=$	$\frac{1 - 5}{2} = \frac{- 4}{2} = - 2$
$x_{2}$	$=$	$\frac{1 + 5}{2} = \frac{6}{2} = 3$

Überprüfe nun, ob das Nennerpolynom an den ermittelten Nullstellen nicht auch Null wird.

$q (x_{1}) = - 15 \neq 0$ , und $q (x_{2}) = 30 \neq 0$ .

Überprüfe nun, ob die Nullstellen im Definitionsbereich der Funktion liegen, indem du die Definitionsmenge $𝔻_{f}$ bestimmst. Setze dazu das Nennerpolynom gleich Null und berechne die Nullstellen von $q (x)$ .

$q (x) = (x - 1) (x^{2} + x + 3) = 0$

Aus dem Linearfaktor $(x - 1)$ kannst du die Nullstelle $x_{q_{1}} = 1$ von $q (x)$ ablesen. Überprüfe $q (x)$ auf weitere Nullstellen. Setze dazu die zweite Klammer gleich Null.

$x^{2} + x + 3$	$=$	$0$
	↓	Mitternachtsformel anwenden.
$x_{q_{2,3}}$	$=$	$\frac{- 1 \pm \sqrt{1^{2} - 4 \cdot 1 \cdot 3}}{2 \cdot 1}$
	$=$	$\frac{- 1 \pm \sqrt{- 11}}{2}$

Da die Diskriminante $D < 0$ , besitzt $q (x)$ keine weiteren Nullstellen. Bestimme die Definitionsmenge $𝔻_{f}$ .

$𝔻_{f} = ℝ ∖ {1}$

Da $x_{1} \in 𝔻_{f}$ und $x_{2} \in 𝔻_{f}$ , hat $f (x)$ zwei Nullstellen bei $x_{1} = - 2$ , $x_{2} = 3$ .

6 Nullstellen von Wurzelfunktionen

Wurzelfunktionen sind Potenzfunktionen in der Form, dass die Variable unter einer Wurzel steht, also $f (x) = \sqrt[n]{x^{m}}$ . Sie bilden damit die Umkehrfunktionen zu Potenzfuktionen der Form $f (x) = x^{n}$ mit $n \in ℕ$ .

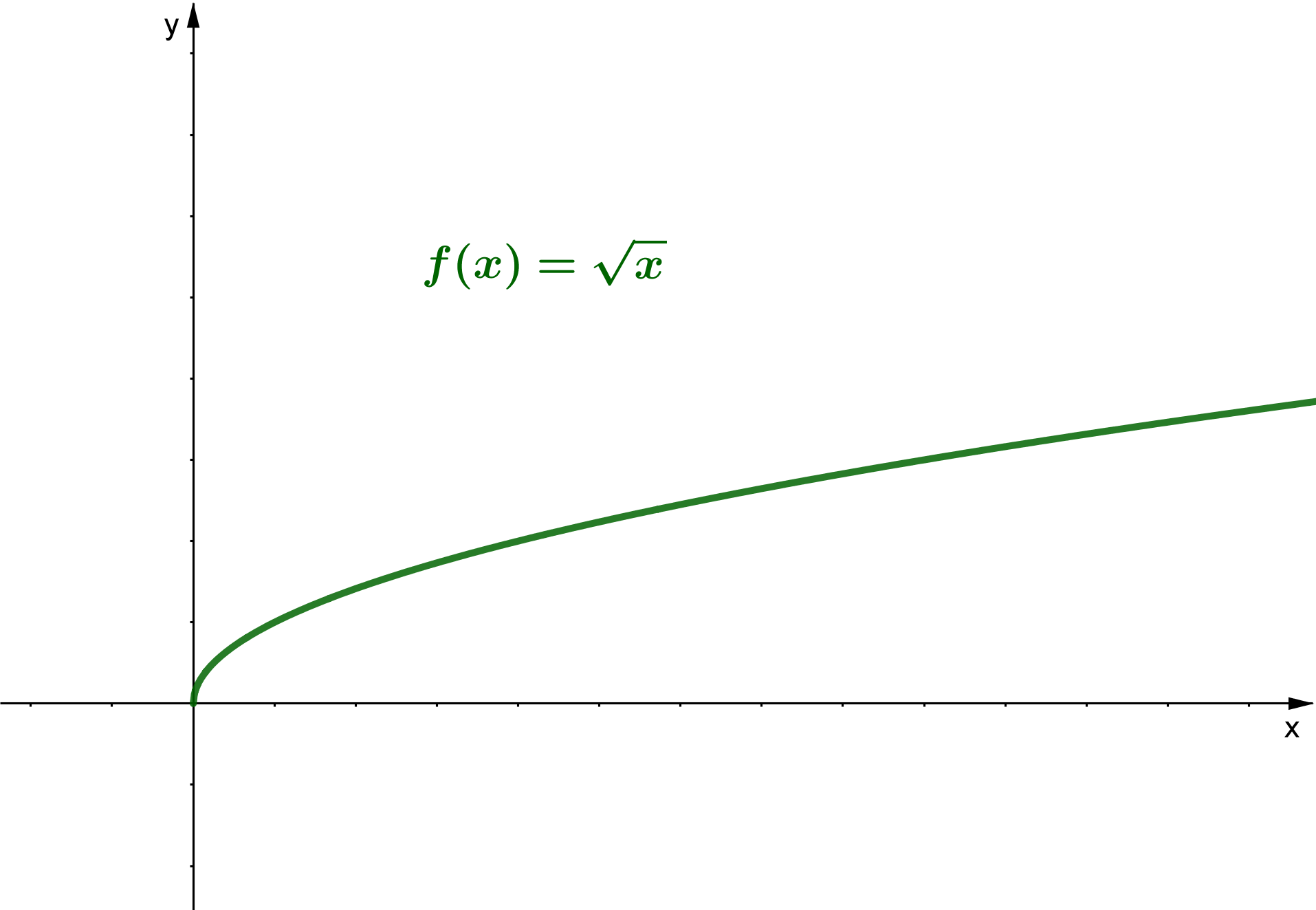
Unter der Wurzel muss nicht nur eine Potenz stehen, sondern die Wurzelfunktion kann auch von der Form $f (x) = \sqrt[n]{g (x)}$ sein, bei der der Radikand $g (x)$ eine beliebige Funktion ist.

Eine Wurzelfunktion nimmt den Wert Null genau dann an, wenn der Radikand Null ist.

Beispiele

a) $f (x) = \sqrt{x^{3} - 4 x} = 0$

Setze den Radikanden $x^{3} - 4 x$ gleich Null.

$\begin{array}{rcl} x^{3} - 4 x = 0 & x ausklammern \\ x \cdot (x^{2} - 4) = 0 & Faktoren = 0 \\ x = 0 oder x^{2} - 4 = 0 & | + 4 \\ x = 0 oder x^{2} = 4 & | \sqrt{} \\ x_{1} = 0 oder x_{2,3} = \pm 2 \end{array}$

Die Funktion $f (x)$ hat drei Nullstellen bei $x_{1} = 0$ , $x_{2} = 2$ , $x_{3} = - 2$ .

b) $f (x) = \sqrt[5]{\sin (3 x - 5)} = 0$

Setze den Radikanden $\sin (3 x - 5)$ gleich Null.

$\sin (3 x - 5) = 0$

$f (x)$ hat somit dieselben Nullstellen wie eine Sinusfunktion der Form $g (x) = \sin (3 x - 5)$ .

Auf den folgenden Kursseiten erfährst du, wie du diese bestimmen kannst.

7 Nullstellen von trigonometrischen Funktionen (1|5)

Die Winkelfunktionen Sinus, Kosinus und Tangens sind die wichtigsten trigonometrischen Funktionen. Sie tauchen sowohl am rechtwinkligen Dreieck, als auch in der Kreisgeometrie (Trigonometrie am Einheitskreis) auf.

Durch die Form ihrer Graphen spielen sie auch eine wichtige Rolle bei der mathematischen Beschreibung von Wellen und Schwingungen.

Trigonometrische Funktionen sind periodisch, d. h. es gibt nicht nur eine oder zwei Nullstellen, sondern entweder unendlich viele oder gar keine.

Trigonometrische Funktionen haben unendlich viele oder gar keine Nullstellen.

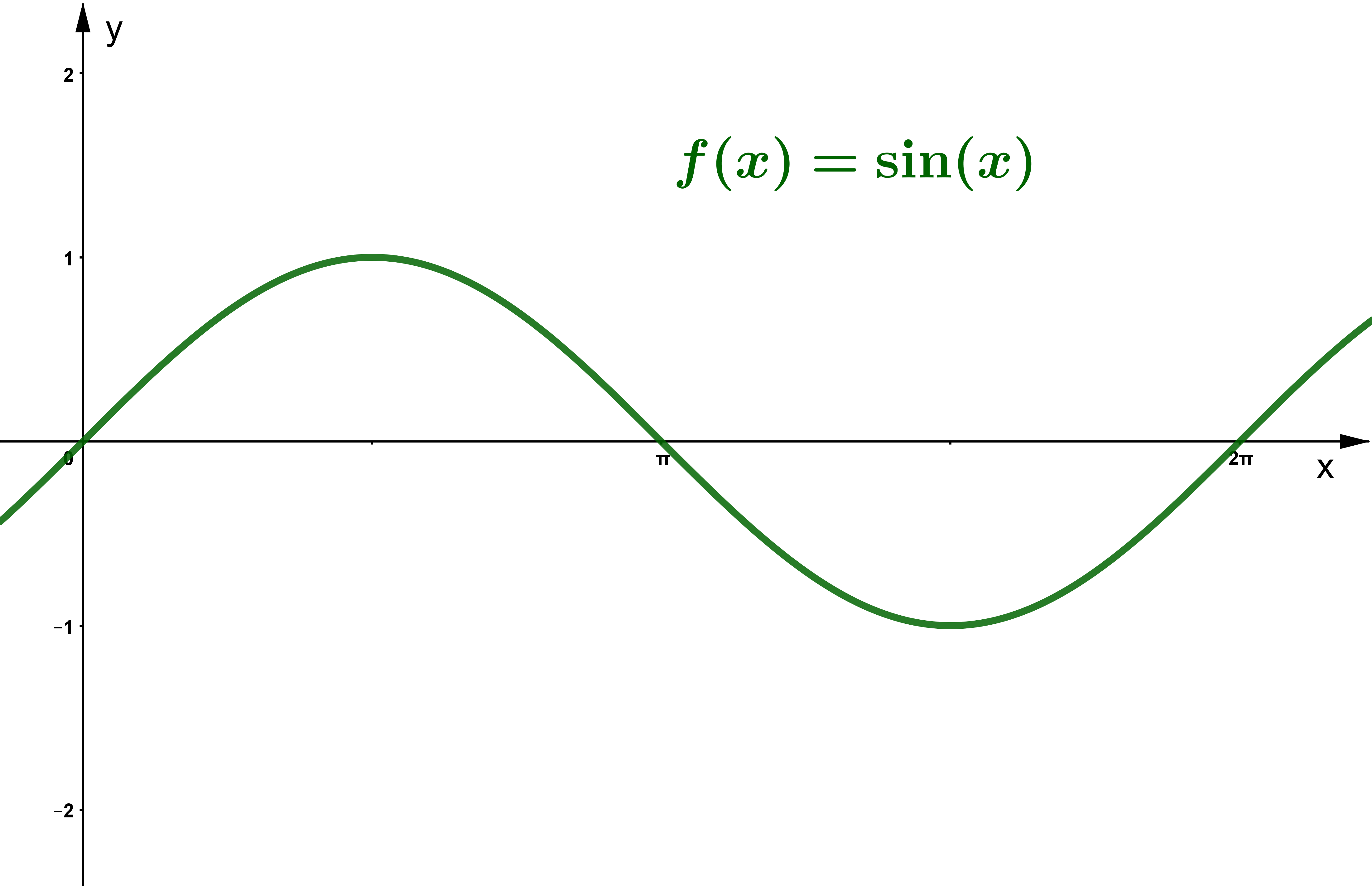
Sinus

Für welche $x \in ℝ$ wird $f (x) = \sin (x)$ Null?

Am Einheitskreis kannst du erkennen, für welche $x \in [0 °; 360 ° [\sin (x)$ Null wird.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.

Es gilt: $360 ° \hat{=} 2 π$ , also für jedes beliebige $α : x = \frac{α}{360 °} \cdot 2 π$ .

Aus dem Einheitskreis kann man ablesen, dass $x_{1} = 0 °$ bzw. $x_{1} = 0$ und $x_{2} = 180 °$ bzw. $x_{2} = π$ Nullstellen im Intervall $[0 °; 360 ° [$ bzw. $[0; 2 π [$ sind.

Da die Sinusfunktion aber periodisch ist, hat sie unendlich viele Nullstellen.

Wir wissen, dass der Sinus an ganzzahligen Vielfachen von $π$ Null wird. Es gilt also: $\sin (k \cdot π) = 0$ mit $k \in ℤ$ .

Die Nullstellenmenge für $f (x) = \sin (x)$ lautet somit: $N = {k \cdot π | k \in ℤ}$ .

8 Nullstellen von trigonometrischen Funktionen (2|5)

Betrachten wir nun eine Sinusfunktion der Form $f (x) = a \cdot \sin (g (x))$ mit $a \neq 0$ , bei der das Argument $g (x)$ eine beliebige Funktion ist.

Da $a \neq 0$ , brauchst du bei der Nullstellenbestimmung $a \cdot \sin (g (x)) = 0$ also nur $\sin (g (x)) = 0$ zu setzen. Wir wissen, dass beim Sinus gilt: $\sin (k \cdot π) = 0$ mit $k \in ℤ$ . Somit gilt zur Nullstellenbestimmung:

$\sin (g (x)) = \sin (k \cdot π) = 0$

$\Rightarrow g (x) = k \cdot π$

Löse diese Gleichung nach $x$ auf, um die Nullstellen von $f (x)$ zu erhalten.

Fazit

Um Nullstellen der Sinusfunktion zu bestimmen, muss man prüfen, wann ihr Argument ein Vielfaches von $π$ wird.

Beispiel

$\begin{matrix} f (x) = 14 \cdot \sin (3 x - 5) = 0 \end{matrix}$

Man weiß, dass $\sin (k \cdot π) = 0$ mit $k \in ℤ$ . Setze das Argument der Sinusfunktion also gleich $k \cdot π$ und löse nach $x$ auf.

$\begin{array}{rcl} 3 x - 5 & = & k \cdot π & | + 5 \\ 3 x & = & k \cdot π + 5 & | : 3 \\ x & = & \frac{k \cdot π + 5}{3} \end{array}$

Stelle das Ergebnis mit einer Nullstellenmenge dar.

$N = {\frac{k \cdot π + 5}{3} | k \in ℤ}$

9 Nullstellen von trigonometrischen Funktionen (3|5)

Als Nächstes schauen wir uns den Cosinus an.

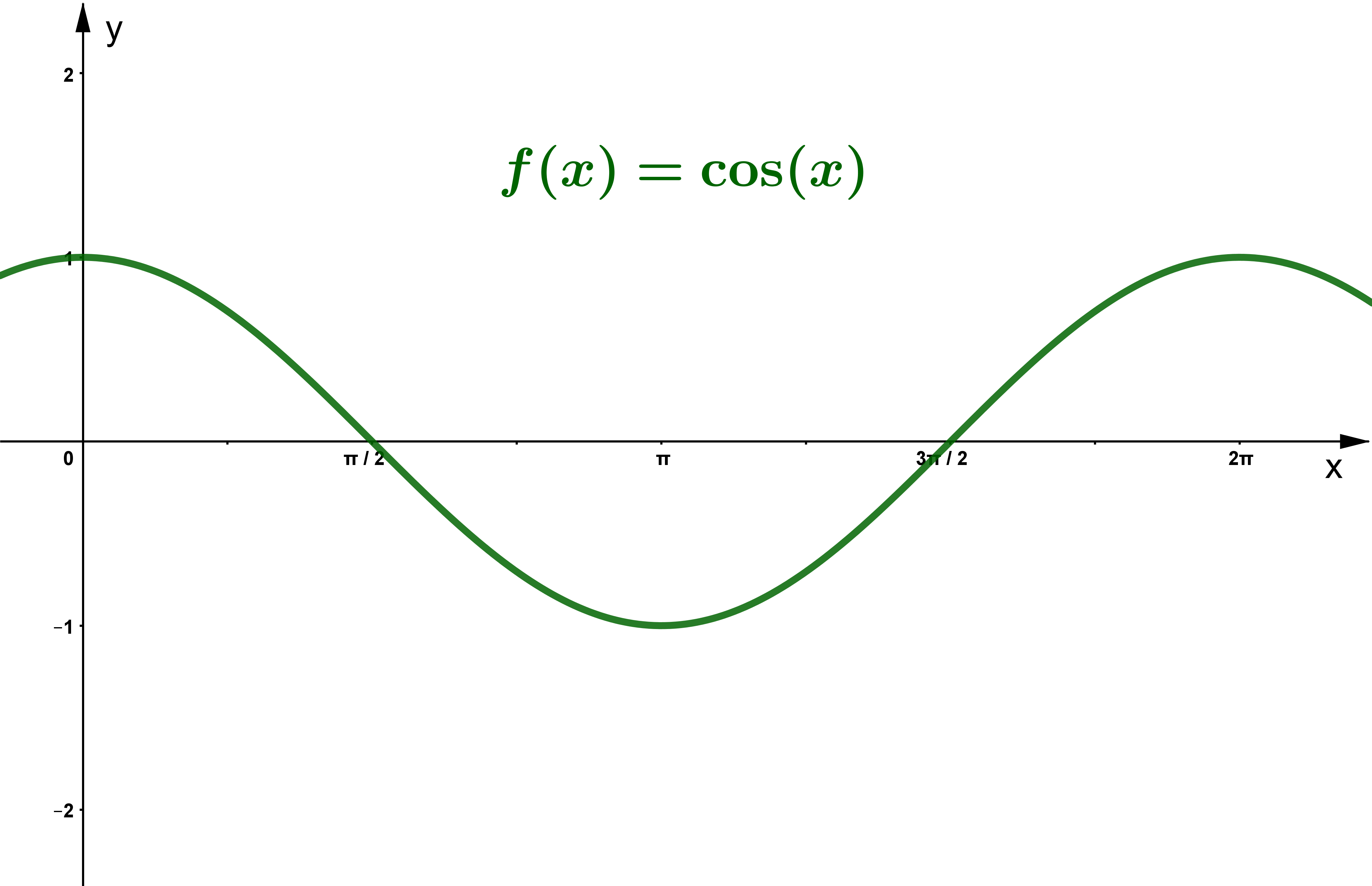
Cosinus

Für welche $x \in ℝ$ wird $f (x) = \cos (x)$ Null?

Am Einheitskreis kannst du erkennen, für welche $x \in [0 °; 360 ° [\cos (x)$ Null wird.

Es gilt: $360 ° \hat{=} 2 π$ , also für jedes beliebige $α : x = \frac{α}{360 °} \cdot 2 π$ .

Aus dem Einheitskreis kann man ablesen, dass $x_{1} = 90 °$ bzw. $x_{1} = \frac{1}{2} π$ und $x_{2} = 270 °$ bzw. $x_{2} = \frac{3}{2} π$ Nullstellen im Intervall $[0 °; 360 ° [$ bzw. $[0; 2 π [$ sind.

Da die Cosinusfunktion aber periodisch ist, hat sie unendlich viele Nullstellen.

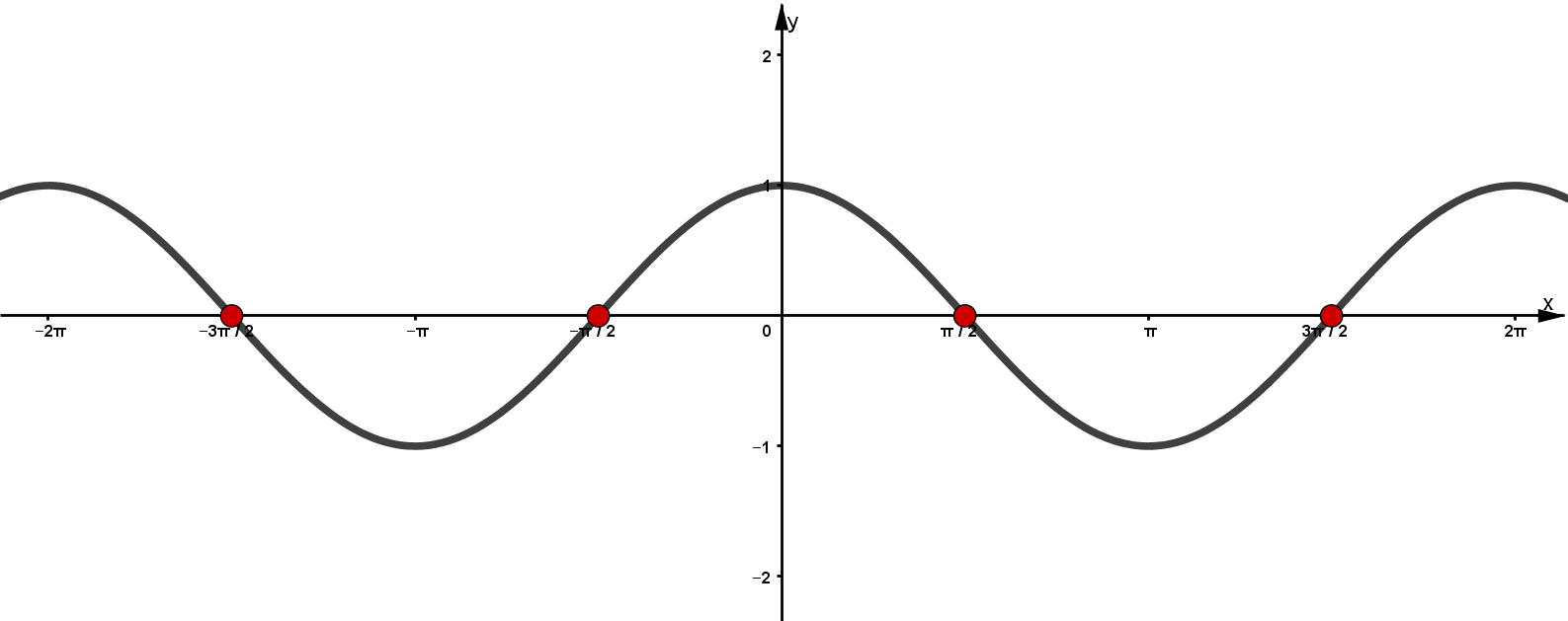
Wir wissen, dass der Cosinus an ungeradzahligen Vielfachen von $\frac{π}{2}$ Null wird. Es gilt also $\cos (k \cdot \frac{π}{2}) = 0$ mit $k = 1,3,5,7,9, \dots$ . Gerade Zahlen sind ein Vielfaches von $2$ . Ungerade Zahlen kann man beschreiben, indem man von einer geraden Zahl $1$ abzieht. Es gilt also $\cos ((2 k - 1) \frac{π}{2}) = 0$ mit $k \in ℤ$ .

Die Nullstellenmenge für $f (x) = \cos (x)$ lautet somit: $N = {(2 k - 1) \frac{π}{2} | k \in ℤ}$ .

10 Nullstellen von trigonometrischen Funktionen (4|5)

Betrachten wir nun eine Cosinusfunktion der Form $f (x) = a \cdot \cos (g (x))$ mit $a \neq 0$ , bei der das Argument $g (x)$ eine beliebige Funktion ist.

Da $a \neq 0$ , brauchst du bei der Nullstellenbestimmung $a \cdot \cos (g (x)) = 0$ also nur $\cos (g (x)) = 0$ zu setzen. Wir wissen, dass beim Cosinus gilt: $\cos ((2 k - 1) \frac{π}{2}) = 0$ mit $k \in ℤ$ . Somit gilt zur Nullstellenbestimmung:

$\cos (g (x)) = \cos ((2 k - 1) \frac{π}{2}) = 0$

$\Rightarrow g (x) = (2 k - 1) \frac{π}{2}$

Löse diese Gleichung nach $x$ auf, um die Nullstellen von $f (x)$ zu erhalten.

Fazit

Um die Nullstellen der Cosinusfunktion zu bestimmen, muss man prüfen, wann ihr Argument ein ungerades Vielfaches von $\frac{π}{2}$ wird.

Beispiel

$f (x) = \cos (x^{2} - 4 π) = 0$

Man weiß, dass $\cos ((2 k - 1) \frac{π}{2}) = 0$ mit $k \in ℤ$ .Setze das Argument der Cosinusfunktion also gleich $(2 k - 1) \frac{π}{2}$ und löse nach $x$ auf.

$\begin{array}{rcl} x^{2} - 4 π & = & (2 k - 1) \frac{π}{2} & | + 4 π \\ x^{2} & = & \frac{(2 k - 1) π}{2} + 4 π & auf Hauptnenner bringen \\ x^{2} & = & \frac{(2 k - 1) π + 8 π}{2} & π ausklammern \\ x^{2} & = & π \cdot \frac{(2 k - 1) + 8}{2} = π \cdot \frac{2 k + 7}{2} & Bruch auftrennen \\ x^{2} & = & π \cdot (\frac{2 k}{2} + \frac{7}{2}) = π \cdot (k + \frac{7}{2}) & | \sqrt{} \\ x & = & \pm \sqrt{π \cdot (k + \frac{7}{2})} \end{array}$

Stelle das Ergebnis mit einer Nullstellenmenge dar.

$N = {\pm \sqrt{π \cdot (k + \frac{7}{2})} | k \in ℤ}$

Da $k$ eine beliebige ganze Zahl ist, kann der Radikand sowohl positive, als auch negative Werte annehmen. Für einen negativen Radikanden gibt es allerdings keine reelle Lösung. Dass das Ergebnis dennoch stimmt, hat damit zu tun, dass die Funktion $f (x) = \cos (x^{2} - 4 π)$ reelle und komplexe Nullstellen hat.

11 Nullstellen von trigonometrischen Funktionen (5|5)

Als Nächstes schauen wir uns noch den Tangens an.

Tangens

Für welche $x \in ℝ$ wird $f (x) = \tan (x)$ Null?

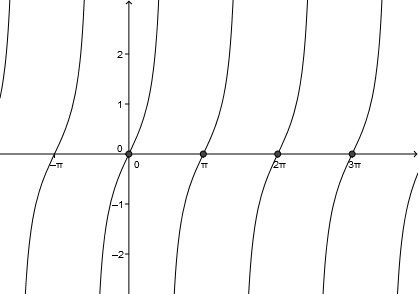
Die Tangensfunktion ist definiert als $\tan (x) = \frac{\sin (x)}{\cos (x)}$ .

Der Tangens wird genau dann Null, wenn der Zähler gleich Null ist. Also $\sin (x) = 0$ .

Somit hat die Tangensfunktion, ebenso wie die Sinusfunktion, Nullstellen bei allen ganzzahligen Vielfachen von $π$ .

$\Rightarrow \tan (k \cdot π) = 0$ mit $k \in ℤ$

Fazit

Um Nullstellen der Tangensfunktion zu bestimmen, muss man prüfen, wann ihr Argument ein Vielfaches von $π$ wird.

12 Nullstellen von Exponentialfunktionen

Eine Exponentialfunktion hat den Funktionsterm $f (x) = b \cdot a^{x}$ . Dabei ist $a > 0, a \neq 1$ und $b \neq 0$ .

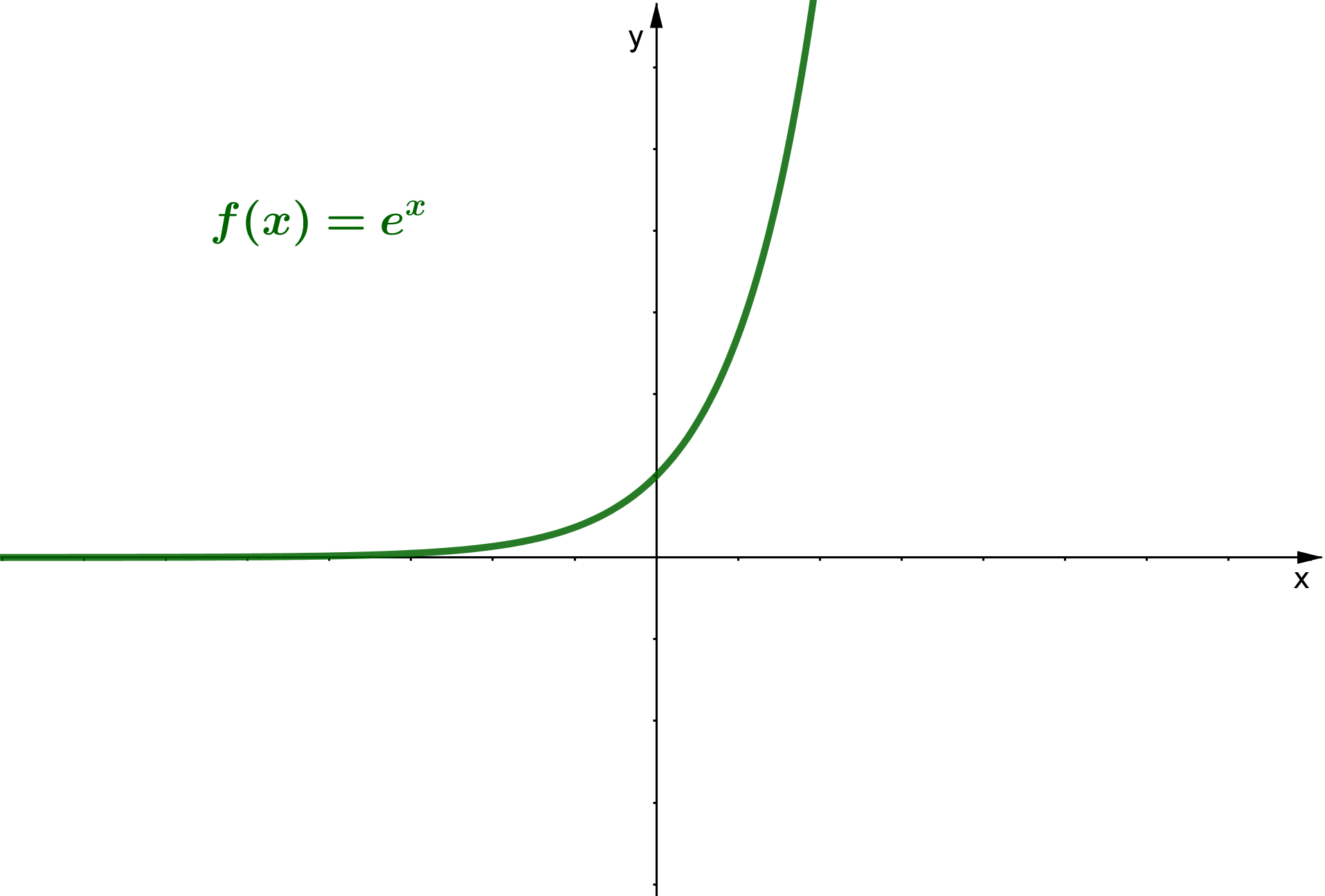
Da $b \neq 0$ , muss zur Bestimmung der Nullstelle $x_{0}$ gelten: $a^{x_{0}} = 0$ . Jedoch gilt: $a^{x} > 0$ . Daraus folgt:

Eine Exponentialfunktion der Form $b \cdot a^{x}$ besitzt keine Nullstellen.

Ausnahme

Wird eine Exponentialfunktion durch eine Konstante $c$ in $y$ -Richtung verschoben, kann es eine Nullstelle geben.

$f (x) = b \cdot a^{x} + c$

$0$	$=$	$b \cdot a^{x_{0}} + c$	$- c$
$- c$	$=$	$b \cdot a^{x_{0}}$	$: b$
$\frac{- c}{b}$	$=$	$a^{x_{0}}$	$\ln ()$
$\ln (\frac{- c}{b})$	$=$	$\ln (a^{x_{0}}) = x_{0} \cdot \ln (a)$	$: \ln (a)$

$\ln (\frac{- c}{b}) = \ln (a^{x_{0}})$	$=$	$x_{0} \cdot \ln (a)$	$: \ln (a)$
$\frac{\ln (\frac{- c}{b})}{\ln (a)}$	$=$	$x_{0}$

Da $a^{x_{0}} > 0$ ist, muss für das Vorhandensein einer Nullstelle $x_{0}$ gelten:

wenn $b > 0$ , dann $c < 0$ .

wenn $b < 0$ , dann $c > 0$ .

Du kannst dir das noch nicht so gut vorstellen? Im folgenden Applet kannst du $a$ , $b$ und $c$ mit den Schiebereglern verändern und schauen, wie sich der Graph der Exponentialfunktion verhält.

13 Nullstellen von Logarithmusfunktionen

Eine Logarithmusfunktion ist eine Abbildung mit der Funktionsvorschrift

$f : ℝ^{+} \to ℝ, x \mapsto \log_{b} (x)$ , wobei $b \in ℝ^{+}$ und $b \neq 1$ gilt.

$b$ heißt Basis des Logarithmus.

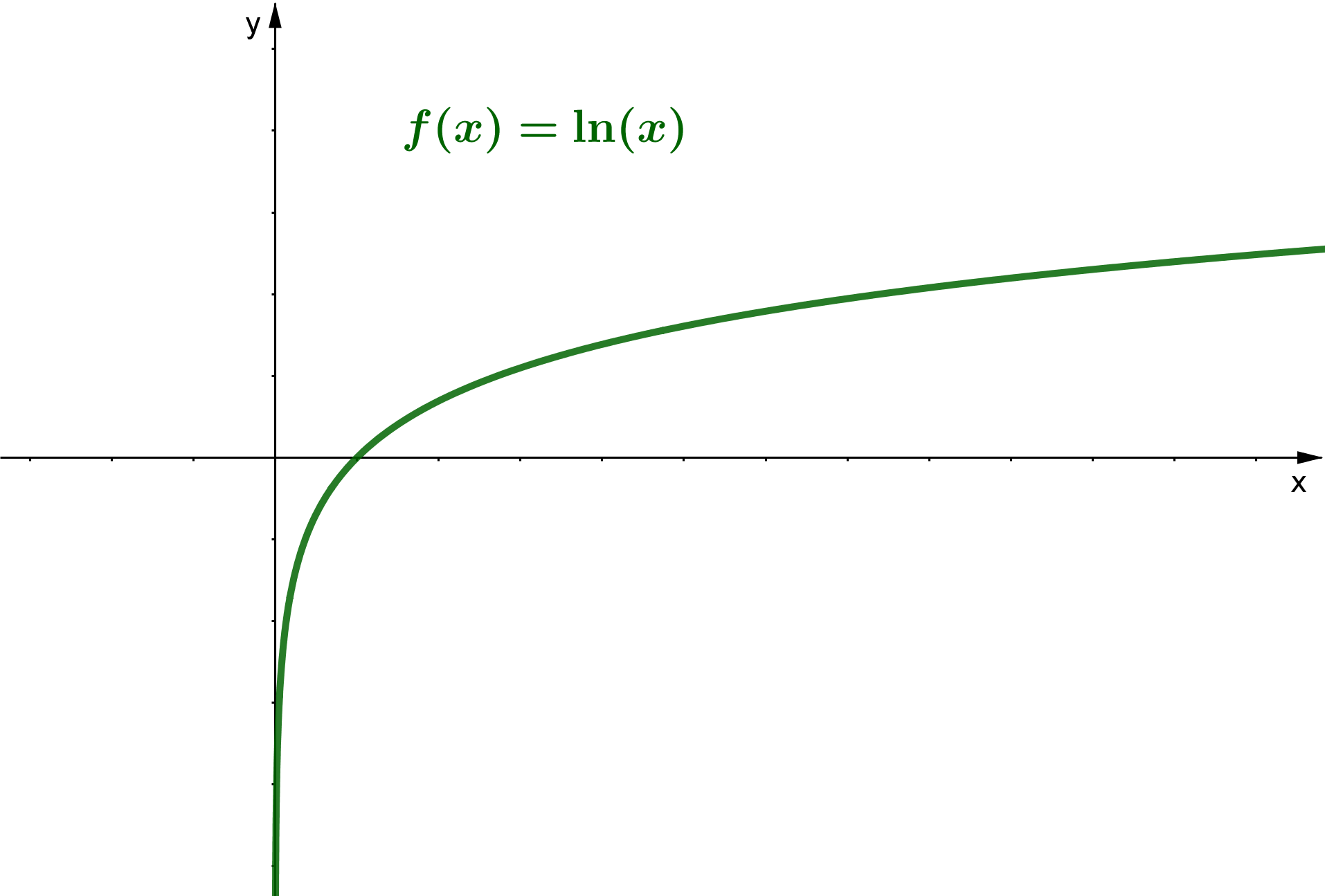
Betrachte eine beliebige Logarithmusfunktion $f (x) = \log_{b} (x)$ . Setze zur Bestimmung der Nullstellen die Funktion gleich Null:

$0 = \log_{b} (x_{0})$

Da die Logarithmusfunktion $y = \log_{b} (x)$ die Umkehrfunktion einer Exponentialfunktion der Form $y = b^{x}$ ist, gilt: $x = b^{y}$ .

Daraus folgt für die Nullstelle: $x_{0} = b^{0} = 1$

$\Rightarrow$ Eine Logarithmusfunktion der Form $f (x) = \log_{b} (x)$ hat die Nullstelle bei $x_{0} = 1$ .

Die Logarithmusfunktion kann auch von der Form $f (x) = \log_{b} (g (x))$ sein, bei der das Argument $g (x)$ eine beliebige Funktion ist.

Allgemein gilt also:

Eine Logarithmusfunktion nimmt genau dann den Wert Null an, wenn ihr Argument 1 ist.

Beispiele

$a) f (x) = \log_{3} (x^{2} - x - 1) = 0$

Setze das Argument $x^{2} - x - 1$ gleich Eins und löse die Gleichung.

$x^{2} - x - 1$	$=$	$1$	$- 1$
$x^{2} - x - 2$	$=$	$0$
	↓	Mitternachtsformel anwenden.
$x_{1,2}$	$=$	$\frac{1 \pm \sqrt{(- 1)^{2} - 4 \cdot 1 \cdot (- 2)}}{2 \cdot 1}$
	$=$	$\frac{1 \pm \sqrt{9}}{2} = \frac{1 \pm 3}{2}$