🎓 Ui, schon Prüfungszeit? Hier geht's zur Mathe-Prüfungsvorbereitung .

Die freie Lernplattform

Nachtermin Teil B

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Für das Viereck $A B C D$ gilt: $A B = 10 cm; B C = 8 cm; A D = 6 cm; ∢ C B A = 90 °; ∢ B A D = 120 °$
Runden Sie im Folgenden auf zwei Stellen nach dem Komma
Zeichnen Sie das Viereck $A B C D$ und berechnen Sie sodann die Länge der Strecke $[B D]$ und das Maß des Winkels $∢ D B A$ .
$[$ Ergebnisse: $B D = 14 cm; ∢ D B A = 21,79 °]$

Teilaufgabe a
Zeichnung des Vierecks $A B C D$ :
Strecke $[A B] = 10 cm$
$∡ B A D = 120 °$
$∡ C B A = 90 °$
$A D = 6 cm$
$B C = 8 cm$
Verbinde abschließend die Punkte $D$ und $C$ .
Länge der Strecke $[B D]$ über den Kosinussatz im Dreieck $A B D$ :
${B D}^{2}$ $=$ ${A B}^{2} + {A D}^{2} - 2 \cdot A B \cdot A D \cdot \cos (∡ B A D)$
${B D}^{2}$ $=$ $(10^{2} + 6^{2} - 2 \cdot 10 \cdot 6 \cdot \cos (120 °)) {cm}^{2}$
$B D$ $=$ $(\sqrt{10^{2} + 6^{2} - 2 \cdot 10 \cdot 6 \cdot \cos (120 °)}) cm$
$B D$ $=$ $14 cm$
Maß des Winkels $∡ D B A$ über den Sinussatz im Dreieck $A B D$ :
$\frac{A D}{\sin (∡ D B A)}$ $=$ $\frac{B D}{\sin (∡ B A D)}$
$\frac{6 cm}{\sin (∡ D B A)}$ $=$ $\frac{14 cm}{\sin (120 °)}$
$\sin (∡ D B A)$ $=$ $\frac{6 cm \cdot \sin (120 °)}{14 cm}$
$\sin (∡ D B A)$ $\approx$ $0,3711$ $\sin^{- 1}$
$∡ D B A$ $\approx$ $21,79 °$

Berechnen Sie den Umfang $u$ des Vierecks $A B C D$ .

Teilaufgabe b
$∡ B A C$ im Dreieck $A B C$ :
$\tan (∡ B A C) = \frac{Gegenkathete}{Ankathete}$
$\tan (∡ B A C) = \frac{B C}{A B} = \frac{8 cm}{10 cm}$
$∡ B A C \approx 38,66 °$
$∡ C A D = 120 ° - ∡ B A C = 120 ° - 38,66 ° \approx 81,34 °$
$A C$ im Dreieck ABC mit dem Satz des Pythagoras:
$A C = \sqrt{{A B}^{2} + {B C}^{2}} = \sqrt{100 {cm}^{2} + 64 {cm}^{2}} = \sqrt{164 {cm}^{2}} \approx 12,81 cm$
$D C$ im Dreieck $A C D$ mithilfe des Kosinussatzes:
${D C}^{2}$ $=$ ${A C}^{2} + {A D}^{2} - 2 \cdot A C \cdot A D \cdot \cos (∡ C A D)$
$D C$ $=$ $(\sqrt{164 + 6^{2} - 2 \cdot \sqrt{164} \cdot 6 \cdot \cos (81,34 °)}) cm$
$D C$ $\approx$ $13,30 cm$
$u = A B + B C + C D + D A = (10 + 8 + 13,30 + 6) cm = 37,30 cm$
Bemerkung: Alternativ könne wir die Länge der Strecke $C D$ auch mit dem Kosinussatz im Dreieck $C B D$ berechnen. Der Winkel $∡ C B D$ ist ja leicht zu berechnen: $∡ C B D = 90^{\circ} - {21,79}^{\circ} = {68,21}^{\circ}$

Der Kreis um $A$ berührt die Strecke $[B D]$ im Punkt $F$ und schneidet die Strecke $[A B]$ im Punkt $G$ .
Zeichnen Sie die Strecke $[A F]$ und den zugehörigen Kreisbogen $\overset{⌢}{G}$ in die Zeichnung zu Teilaufgabe a) ein.
Berechnen Sie sodann den Flächeninhalt $A$ der Figur, die durch die Strecken $[G B]$ , $[B F]$ und den Kreisbogen $\overset{⌢}{G}$ begrenzt wird.
$[$ Teilergebnis: $A F = 3,71 cm]$

Zeichnung der Strecke $[A F]$ und des Kreisbogens $\overset{⌢}{G}$ :
Der Kreis $A$ berührt die Strecke $[D B]$ im Punkt $F$ , daher muss die Strecke $[A F]$ in einem rechten Winkel zu $[D B]$ stehen: Fälle der Lot von $A$ auf die Strecke $[D B]$ .
Schnittpunk der Strecke $[D B]$ und der Senkrechten $] A F [$ ist der Punkt $F$ .
Zeichne nun den Kreis um $A$ mit Radius $r = [A F]$ .
Der Schnittpunkt der Kreislinie und der Strecke $[A B]$ ist der Punkt $G$ .
Flächeninhalt $A$ der entstandenen Figur $G B F$ :
$A = A_{Dreieck (A B F)} - A_{Kreissektor (A G F)}$
Fläche des Dreiecks $A B F$ :
$A F$ im rechtwinkligen Dreieck $A B F$ mithilfe der Trigonometrie
( $∡ F B A = ∡ D B A$ ):
$\sin (∡ F B A)$ $=$ $\frac{Gegenkathete}{Hypotenuse}$
$\sin (∡ F B A)$ $=$ $\frac{A F}{A B}$
$\sin (21,79 °)$ $=$ $\frac{A F}{10 cm}$ $\cdot 10 cm$
$A F$ $=$ $\sin (21,79 °) \cdot 10 cm$
$A F$ $\approx$ $3,71 cm$
Bemerkung: Alternativ können wir die Länge von $F B$ auch mit dem Satz des Pythagoras berechnen, die Längen von $A F$ und $A B$ sind ja bekannt.
$F B$ im rechtwinkligen Dreieck $A B F$ mithilfe der Trigonometrie
$\tan (∡ F B A)$ $=$ $\frac{Gegenkathete}{Ankathete}$
$\tan (∡ F B A)$ $=$ $\frac{A F}{F B}$
$\tan (21,79 °)$ $=$ $\frac{3,71 cm}{F B}$
$F B$ $=$ $\frac{3,71 cm}{\tan (21,79 °)}$
$F B$ $\approx$ $9,28 cm$
$A_{Dreieck} = \frac{1}{2} \cdot A F \cdot F B = \frac{1}{2} \cdot 3,71 cm \cdot 9,28 cm \approx 17,22 {cm}^{2}$
Fläche des Kreissektors: $A_{s} = r^{2} \cdot π \cdot \frac{α}{360 °}$
$α$ im Dreieck $A B F$ über die Innenwinkelsumme im Dreieck:
$α = ∡ B A F = 180 ° - 90 ° - ∡ D B A = 180 ° - 90 ° - 21,79 ° = 68,21 °$
$A_{Kreissektor} = r^{2} \cdot π \cdot \frac{α}{360 °} = {A F}^{2} \cdot π \cdot \frac{α}{360 °} = {(3,71 cm)}^{2} \cdot π \cdot \frac{68,21 °}{360 °} \approx 8,19 {cm}^{2}$
$A = A_{Dreieck} - A_{Kreissektor} = 17,22 {cm}^{2} - 8,19 {cm}^{2} \approx 9,03 {cm}^{2}$

Punkte $H_{n}$ auf der Strecke $[B D]$ mit $H_{n} B (x) = x cm$ bilden für $x \in] 0; 14 [$ und $x \in ℝ$ zusammen mit dem Punkt $C$ Strecken $[H_{n} C]$ .
Zeichnen Sie die Strecke $[H_{1} C]$ für $x = 6$ in die Zeichnung zu Teilaufgabe a) ein.
Zeigen Sie sodann rechnerisch, dass für die Länge der Strecken $[H_{n} C]$ in Abhängigkeit von $x$ gilt: $H_{n} C (x) = \sqrt{x^{2} - 5,94 x + 64} cm$ .

Teilaufgabe d
Zeichnung der Strecke $[$ $H_{1} C$ $]$ für $x = 6$
$H_{1} B = 6 cm$ (pink) und $H_{1} B \in [B D]$
Verbinde die Punkte $H_{1}$ und $C$
Länge der Strecke $H_{1} C$ in Abhängigkeit von $x$ mithilfe des Kosinussatzes im Dreieck $B C H_{1}$ :
Winkel $C B H_{1}$ : $∡ C B H_{1} = ∡ C B A - ∡ D B A = 90 ° - 21,79 ° = 68,21 °$
${H_{n} C}^{2} (x)$ $=$ ${B H_{n}}^{2} + {B C}^{2} - 2 \cdot B H_{n} \cdot B C \cdot \cos (∡ C B H_{1})$
${H_{n} C}^{2} (x)$ $=$ $(x^{2} + 8^{2} - 2 \cdot x \cdot 8 \cdot \cos (68,21 °)) {cm}^{2}$ $\sqrt{}$
$H_{n} C (x)$ $=$ $(\sqrt{x^{2} + 8^{2} - 2 \cdot x \cdot 8 \cdot \cos (68,21 °)}) cm$
$H_{n} C (x)$ $=$ $(\sqrt{x^{2} + 64 - 5,94 \cdot x}) cm$
$H_{n} C (x)$ $=$ $(\sqrt{x^{2} - 5,94 x + 64}) cm$

Unter den Strecken $[H_{n} C]$ hat die Strecke $[H_{0} C]$ die minimale Länge.
Berechnen Sie den zugehörigen Wert für $x$ und die Länge der Strecke $[H_{0} C]$ .

Teilaufgabe e
Der zugehörige Wert $x$ für $[H_{0} C]$ :
Die Strecke $[H_{n} C]$ ist minimal, wenn $[H_{n} C]$ senkrecht auf $[D B]$ steht (siehe Bild).
Das Dreieck $H_{0} B C$ ist rechtwinklig, somit kannst du die Länge $H_{0} C (x)$ mithilfe der Trigonometrie berechnen:
$\cos (∡ C B H_{0}) = \frac{Ankathete}{Hypotenuse}$
$\cos (∡ C B H_{0}) = \frac{H_{0} B}{B C}$
$\cos (68,21 °) = \frac{x}{8}$
$x = \cos (68,21 °) \cdot 8 \approx 2,97$
Wenn du die genaue Länge $H_{0} C$ berechnen willst, kannst du x in die obige Gleichung einsetzen:
$H_{0} C = (\sqrt{x^{2} - 5,94 x + 64}) cm = (\sqrt{{2,97}^{2} - 5,94 \cdot 2,97 + 64}) cm \approx 7,43 cm$

Überprüfen Sie durch Rechnung, ob das Dreieck $B C F$ gleichschenklig ist.
Das Dreieck $B C F$ ist gleichschenklig.
Das Dreieck $B C F$ ist nicht gleichschenklig.

Teilaufgabe f
Das Dreieck $B C F$ ist nicht gleichschenklig:
Die Länge $C F$ mithilfe des Kosinussatzes:
${C F}^{2} = {B F}^{2} + {B C}^{2} - 2 \cdot B F \cdot B C \cdot \cos (∡ C B F)$
${C F}^{2} = ({9,28}^{2} + 8^{2} - 2 \cdot 9,28 \cdot 8 \cdot \cos (68,21 °)) {cm}^{2}$
$C F = (\sqrt{{9,28}^{2} + 8^{2} - 2 \cdot 9,28 \cdot 8 \cdot \cos (68,21 °)}) cm$
$C F \approx 9,75 cm$
$B C = 8 cm$ und in Aufgabe c) berechnet $B F = 9,28 cm$
Es ist also: $B C < B F < C F$
Damit ist das Dreieck $B C F$ nicht gleichschenklig.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Das Drachenviereck $A B C D$ ist die Grundfläche der Pyramide $A B C D S$ . Die Spitze $S$ der Pyramide liegt senkrecht über dem Schnittpunkt $M$ der Diagonalen des Drachenvierecks $A B C D$ (siehe Skizze).
Es gilt: $A C = 10 cm; B D = 8 cm; A M = 3 cm; M S = 9 cm .$
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
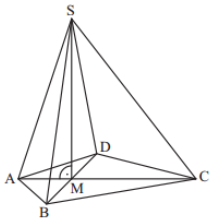
Zeichnen Sie das Schrägbild der Pyramide $A B C D S$ , wobei die Strecke $[A C]$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $C$ liegen soll.
Für die Zeichnung gilt: $q = \frac{1}{2}; ω = 45 °$ .
Berechnen Sie sodann die Länge der Strecke $[S C]$ und das Maß des Winkels $∢ S C A$ .
$[$ Ergebnisse: $S C = 11,40 cm$ und $∢ S C A = 52,13 °$ $]$

Teilaufgabe a
Schrägbild der Pyramide $A B C D S$ :
$A C = 10 cm$
$A M = 3 cm$
$M S = 9 cm$ und steht senkrecht auf $[A C]$
Die Grundfläche ist ein Drachenviereck, daher wissen wir, dass die Diagonalen senkrecht aufeinander stehen. Da $ω = 45 °$ ist, zeichnen wir eine Gerade durch $M$ im Winkel von 45°
$[A C]$ ist die Symmetrieachse, daher sind $[B M] = [M D] = 4 cm$ . In unserem Fall haben wir den Verkürzungsfaktor $q = \frac{1}{2}$ im Schrägbild, also ist $[B M] = [M D] = 2 cm$ .
Verbinde nun alle Eckpunkte der Pyramide miteinander.
Länge der Strecke $S C$ im rechtwinkligen Dreieck $M C S$ mit dem Satz des Pythagoras:
${S C}^{2} = {M C}^{2} + {M S}^{2}$
$S C = \sqrt{{M C}^{2} + {M S}^{2}} = \sqrt{{(10 cm - 3 cm)}^{2} + {(9 cm)}^{2}} = (\sqrt{130 cm}) c m \approx 11,40 cm$
Maß des Winkels $∡ S C A (∡ S C A = ∡ S C M)$ :
Wir berechnen den Winkel $∡ S C M$ im rechtwinkligen Dreieck $M C S$ (siehe Zeichnung oben) mithilfe der Trigonometrie:
$\tan (∡ S C M)$ $=$ $\frac{Gegenkathete}{Ankathete}$
$\tan (∡ S C M)$ $=$ $\frac{M S}{M C}$
$\tan (∡ S C M)$ $=$ $\frac{9 cm}{(10 - 3) cm}$
$\tan (∡ S C M)$ $=$ $1, 285714$ $\tan^{- 1}$
$∡ S C M$ $\approx$ $52,13 °$

Auf der Strecke $[A S]$ liegt der Punkt $P$ mit $S P = 4 cm$ . Punkte $Q_{n}$ auf der Seitenkante $[S C]$ bilden zusammen mit den Punkten $P$ und $S$ Dreiecke $P Q_{n} S$ .
Im Dreieck $P Q_{1} S$ gilt: $[P Q_{1}] ⟂ [S C]$ ; im Dreieck $P Q_{2} S$ gilt: $[P Q_{2}] ∥ [A C]$ .
Zeichnen Sie die Dreiecke $P Q_{1} S$ und $P Q_{2} S$ in das Schrägbild zu Teilaufgabe a) ein.

Teilaufgabe b
Zeichnung des Dreiecks $P Q_{1} S$ :
Der Punkt $P \in [A S]$ und $S P = 4 cm$ (rot).
$[P Q_{1}] ⟂ [S C]$ : Wir können also ein Lot von Punkt $P$ auf die Seite $[S C]$ fällen (grün).
Der Schnittpunkt der Lotgeraden und der Seite $[S C]$ ist der Punkt $Q_{1}$ .
Zeichnung des Dreiecks $P Q_{2} S$ :
Da $[P Q_{2}] ∥ [A C]$ sein soll, zeichnen wir eine Parallele durch den Punkt $P$ zur Seite $[A C]$ (blau).
Der Schnittpunkt der Parallelen und der Seite $[S C]$ ist der Punkt $Q_{2}$ .

Berechnen Sie die Länge der Strecke $[S Q_{1}]$ .
$[$ Teilergebnis: $∢ A S C = 56,30 °$ $]$

Teilaufgabe c
Länge der Strecke $[$ $S Q_{1}$ $]$ im rechtwinkligen Dreieck $P Q_{1} S$ (pink) mithilfe der Trigonometrie:
Da wir nur eine Seite in diesem Dreieck ( $[S P] = 4 cm$ ) kennen, fehlt uns noch ein Winkel oder eine zweite Seite, um die gesuchte Seite $[S Q_{1}]$ berechnen zu können.
Der Winkel $∡ P S Q_{1} = ∡ A S C$ (blau in der Abbildung unten):
Der Winkel liegt auch im Dreieck $A C S$ (Abbildung rechts), von dem wir bereits einen zweiten Winkel, den Winkel $∡ S C M = ∡ S C A$ (grün) $= 52,13 °$ kennen.
$∡ C A S$ (rot) mithilfe der Trigonometrie im rechtwinkligen Dreieck $A M S$ :
$\tan (∡ C A S) = \frac{Gegenkathete}{Ankathete} = \frac{S M}{A M}$
$\tan (∡ C A S) = \frac{9 cm}{3 cm}$ | $\cdot \tan^{- 1}$
$∡ C A S \approx 71,57 °$
$∡ A S C$ (blau) können wir mit der Innenwinkelsumme im Dreieck $A C S$ berechnen:
$∡ A S C = 180 ° - 52,13 ° - 71,57 ° \approx 56,30 °$
Nun können wir endlich die Länge der Strecke $S Q_{1}$ berechnen:
$\cos (∡ A S C)$ $=$ $\frac{Ankathete}{Hypotenuse}$
$\cos (∡ A S C)$ $=$ $\frac{S Q_{1}}{S P}$
$\cos (56,30 °)$ $=$ $\frac{S Q_{1}}{4 cm}$ $\cdot 4 cm$
$S Q_{1}$ $=$ $\cos (56,30 °) \cdot 4 cm$
$S Q_{1}$ $\approx$ $2,22 cm$
Bemerkung: alternativ können wir auch im rechtwinkligen Dreieck $A M S$ den Wert von $A S$ mit dem Satz des Pythagoras als $\sqrt{3^{2} + 9^{2}} = \sqrt{90}$ berechnen. Dann verwenden wir den Sinussatz und erhalten den Sinus von $∡ A S C$ durch Auflösen von
$\frac{\sin ∡ A S C}{10} = \frac{\sin {52,15}^{°}}{\sqrt{90}}$

Berechnen Sie den Flächeninhalt $A$ des Dreiecks $P Q_{2} S$ .

Teilaufgabe d
Flächeninhalt $A$ des Dreiecks $P Q_{2} S$ :
$A_{D r e i e c k} = \frac{1}{2} \cdot S P \cdot P Q_{2} \cdot \sin (∡ Q_{2} P S)$
Uns fehlt also die Strecke $P Q_{2}$ und der Winkel $∡ Q_{2} P S$ :
Winkel $∡ Q_{2} P S$ :
Betrachten wir die Dreiecke $S P Q_{2}$ und $S A C$ , sehen wir, dass sie die gleiche Spitze haben, außerdem ist $P Q_{2} ∥ A C$ (zentrische Streckung), somit sind sie auch winkeltreu.
$∡ Q_{2} P S = ∡ C A S = 71,57 °$ wie in Teilaufgabe c) berechnet.
Strecke ${P Q}_{2}$ mit dem Sinussatz im Dreieck $S P Q_{2}$ :
$\frac{P S}{\sin (∡ S Q_{2} P)}$ $=$ $\frac{P Q_{2}}{\sin (∡ A S C)}$
$\frac{4 cm}{\sin (52,13 °)}$ $=$ $\frac{P Q_{2}}{\sin (56,30 °)}$ $\cdot \sin (56,30 °)$
$P Q_{2}$ $=$ $\frac{4 cm \cdot \sin (56,30 °)}{\sin (52,13 °)}$
$P Q_{2}$ $\approx$ $4,22 cm$
Nun können wir die Fläche $A$ berechnen:
$A_{D r e i e c k} = \frac{1}{2} \cdot S P \cdot P Q_{2} \cdot \sin (∡ Q_{2} P S) = \frac{1}{2} \cdot 4 cm \cdot 4,22 cm \cdot \sin (71,57 °) \approx 8,01 {cm}^{2}$

Im Dreieck $P Q_{3} S$ hat der Winkel $∢ Q_{3} P S$ das Maß $77 °$ . Der Punkt $Q_{3}$ ist die Spitze der Pyramide $A B C D Q_{3}$ mit dem Höhenfußpunkt $F_{3}$ und der Höhe $[F_{3} Q_{3}]$ .
Zeichnen Sie die Pyramide $A B C D Q_{3}$ mit der Höhe $[F_{3} Q_{3}]$ in das Schrägbild zu Teilaufgabe a) ein und berechnen Sie sodann die Länge der Strecke $[F_{3} Q_{3}]$ .

Teilaufgabe e
Zeichnung der Pyramide $A B C D Q_{3}$ :
$∡ Q_{3} P S = 77 °$
Der Schnittpunkt mit der Seite $[S C]$ bildet die Spitze der Pyramide $A B C D Q_{3}$ .
Verbinde nun alle Eckpunkte miteinander.
Fälle jetzt das Lot von $Q_{3}$ auf die Diagonale auf $[A C]$ , der Schnittpunkt ist der Fußpunkt $F$ der Höhe der Pyramide.
Länge der Höhe [ $Q_{3} F_{3}$ ] der Pyramide $A B C D Q_{3}$ im rechtwinkligen Dreieck $F_{3} C Q_{3}$ mit der Trigonometrie:
$\sin (∡ A C S) = \frac{Gegenkathete}{Hypotenuse} = \frac{Q_{3} F_{3}}{Q_{3} Q}$
Uns fehlt in dieser Formel die Seite $Q_{3} C$ . Aber: $Q_{3} C = S C - S Q_{3}$ .
Somit brauchen wir auch $S Q_{3}$ im Dreieck $S P Q_{3}$ mit dem Sinussatz:
$∡ S Q_{3} P = 180 ° - ∡ A S C - ∡ S P Q_{3} = 180 ° - 56,30 ° - 77 ° = 46,70 °$
$\frac{S P}{\sin (∡ S Q_{3} P)}$ $=$ $\frac{S Q_{3}}{\sin (∡ S P Q_{3})}$
$\frac{4 cm}{\sin (46,70 °)}$ $=$ $\frac{S Q_{3}}{\sin (77^{°})}$ $\cdot \sin (77 °)$
$S Q_{3}$ $=$ $\frac{4 cm \cdot \sin (77 °)}{\sin (46,70 °)}$
$S Q_{3}$ $=$ $5,36 cm$
$Q_{3} C = S C - S Q_{3} = 11,40 cm - 5,36 cm \approx 6,04 cm$
$\sin (∡ S C A) = \frac{Q_{3} F_{3}}{Q_{3} C}$
$\sin (52,13 °) = \frac{Q_{3} F_{3}}{6,04 cm}$
$Q_{3} F_{3_{}} = 6,04 cm \cdot \sin (52,13 °) \approx 4,77 cm$

Berechnen Sie das Volumen der Pyramiden $A B C D Q_{n}$ in Abhängigkeit von der Länge der Strecke $[S Q_{n}]$ mit $S Q_{n} (x) = x cm$ und $x \in ℝ$ ; $x \in] 0; 11,40 [.$

Teilaufgabe f
Volumen der Pyramiden $A B C D Q_{n}$ mit $S Q_{n} (x) = x$ :
$V_{A B C D Q_{n}} = \frac{1}{3} \cdot G_{D r a c h e} \cdot h$
Für die Höhe $h = Q_{n} F_{n}$ gehen wir wie oben vor:
$Q_{n} C = S C - S Q_{n} = 11,40 cm - x$
$\sin (∡ S C A)$ $=$ $\frac{Q_{n} F_{n}}{Q_{3} C}$
$\sin (52,13 °)$ $=$ $\frac{Q_{n} F_{n}}{11,40 cm - x}$
$Q_{n} F_{n}$ $=$ $\sin (52,13 °) (11,40 cm - x)$
$Q_{n} F_{n}$ $=$ $9,00 cm - \sin (52,13 °) \cdot x$
$Q_{n} F_{n}$ $=$ $9,00 cm - 0,79 x$
Für die Grundfläche $G = e \cdot f$ mit $e = B D = 8 cm$ und $f = A C = 10 cm$ :
$G_{D r a c h e} = \frac{1}{2} \cdot e \cdot f = \frac{1}{2} \cdot 8 \cdot 10 {cm}^{2} = 40 {cm}^{2}$
$V_{A B C D Q_{n}} (x) = \frac{1}{3} \cdot G_{D r a c h e} \cdot h = \frac{1}{3} \cdot 40 {cm}^{2} \cdot (9,00 cm - 0,79 x) = (120 - 10,53 x) {cm}^{3}$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org