Nachtermin Teil B

Das Drachenviereck $A B C D$ ist die Grundfläche der Pyramide $A B C D S$ . Die Spitze $S$ der Pyramide liegt senkrecht über dem Schnittpunkt $M$ der Diagonalen des Drachenvierecks $A B C D$ (siehe Skizze).

Es gilt: $A C = 10 cm; B D = 8 cm; A M = 3 cm; M S = 9 cm .$

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

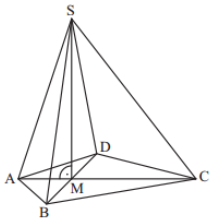
Zeichnen Sie das Schrägbild der Pyramide $A B C D S$ , wobei die Strecke $[A C]$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $C$ liegen soll.
Für die Zeichnung gilt: $q = \frac{1}{2}; ω = 45 °$ .
Berechnen Sie sodann die Länge der Strecke $[S C]$ und das Maß des Winkels $∢ S C A$ .
$[$ Ergebnisse: $S C = 11,40 cm$ und $∢ S C A = 52,13 °$ $]$
Teilaufgabe a
Schrägbild der Pyramide $A B C D S$ :
$A C = 10 cm$
$A M = 3 cm$
$M S = 9 cm$ und steht senkrecht auf $[A C]$
Die Grundfläche ist ein Drachenviereck, daher wissen wir, dass die Diagonalen senkrecht aufeinander stehen. Da $ω = 45 °$ ist, zeichnen wir eine Gerade durch $M$ im Winkel von 45°
$[A C]$ ist die Symmetrieachse, daher sind $[B M] = [M D] = 4 cm$ . In unserem Fall haben wir den Verkürzungsfaktor $q = \frac{1}{2}$ im Schrägbild, also ist $[B M] = [M D] = 2 cm$ .
Verbinde nun alle Eckpunkte der Pyramide miteinander.
Länge der Strecke $S C$ im rechtwinkligen Dreieck $M C S$ mit dem Satz des Pythagoras:
${S C}^{2} = {M C}^{2} + {M S}^{2}$
$S C = \sqrt{{M C}^{2} + {M S}^{2}} = \sqrt{{(10 cm - 3 cm)}^{2} + {(9 cm)}^{2}} = (\sqrt{130 cm}) c m \approx 11,40 cm$
Maß des Winkels $∡ S C A (∡ S C A = ∡ S C M)$ :
Wir berechnen den Winkel $∡ S C M$ im rechtwinkligen Dreieck $M C S$ (siehe Zeichnung oben) mithilfe der Trigonometrie:
$\tan (∡ S C M)$ $=$ $\frac{Gegenkathete}{Ankathete}$
$\tan (∡ S C M)$ $=$ $\frac{M S}{M C}$
$\tan (∡ S C M)$ $=$ $\frac{9 cm}{(10 - 3) cm}$
$\tan (∡ S C M)$ $=$ $1, 285714$ $\tan^{- 1}$
$∡ S C M$ $\approx$ $52,13 °$
Auf der Strecke $[A S]$ liegt der Punkt $P$ mit $S P = 4 cm$ . Punkte $Q_{n}$ auf der Seitenkante $[S C]$ bilden zusammen mit den Punkten $P$ und $S$ Dreiecke $P Q_{n} S$ .
Im Dreieck $P Q_{1} S$ gilt: $[P Q_{1}] ⟂ [S C]$ ; im Dreieck $P Q_{2} S$ gilt: $[P Q_{2}] ∥ [A C]$ .
Zeichnen Sie die Dreiecke $P Q_{1} S$ und $P Q_{2} S$ in das Schrägbild zu Teilaufgabe a) ein.
Teilaufgabe b
Zeichnung des Dreiecks $P Q_{1} S$ :
Der Punkt $P \in [A S]$ und $S P = 4 cm$ (rot).
$[P Q_{1}] ⟂ [S C]$ : Wir können also ein Lot von Punkt $P$ auf die Seite $[S C]$ fällen (grün).
Der Schnittpunkt der Lotgeraden und der Seite $[S C]$ ist der Punkt $Q_{1}$ .
Zeichnung des Dreiecks $P Q_{2} S$ :
Da $[P Q_{2}] ∥ [A C]$ sein soll, zeichnen wir eine Parallele durch den Punkt $P$ zur Seite $[A C]$ (blau).
Der Schnittpunkt der Parallelen und der Seite $[S C]$ ist der Punkt $Q_{2}$ .
Berechnen Sie die Länge der Strecke $[S Q_{1}]$ .
$[$ Teilergebnis: $∢ A S C = 56,30 °$ $]$

Teilaufgabe c
Länge der Strecke $[$ $S Q_{1}$ $]$ im rechtwinkligen Dreieck $P Q_{1} S$ (pink) mithilfe der Trigonometrie:
Da wir nur eine Seite in diesem Dreieck ( $[S P] = 4 cm$ ) kennen, fehlt uns noch ein Winkel oder eine zweite Seite, um die gesuchte Seite $[S Q_{1}]$ berechnen zu können.
Der Winkel $∡ P S Q_{1} = ∡ A S C$ (blau in der Abbildung unten):
Der Winkel liegt auch im Dreieck $A C S$ (Abbildung rechts), von dem wir bereits einen zweiten Winkel, den Winkel $∡ S C M = ∡ S C A$ (grün) $= 52,13 °$ kennen.
$∡ C A S$ (rot) mithilfe der Trigonometrie im rechtwinkligen Dreieck $A M S$ :
$\tan (∡ C A S) = \frac{Gegenkathete}{Ankathete} = \frac{S M}{A M}$
$\tan (∡ C A S) = \frac{9 cm}{3 cm}$ | $\cdot \tan^{- 1}$
$∡ C A S \approx 71,57 °$
$∡ A S C$ (blau) können wir mit der Innenwinkelsumme im Dreieck $A C S$ berechnen:
$∡ A S C = 180 ° - 52,13 ° - 71,57 ° \approx 56,30 °$
Nun können wir endlich die Länge der Strecke $S Q_{1}$ berechnen:
$\cos (∡ A S C)$ $=$ $\frac{Ankathete}{Hypotenuse}$
$\cos (∡ A S C)$ $=$ $\frac{S Q_{1}}{S P}$
$\cos (56,30 °)$ $=$ $\frac{S Q_{1}}{4 cm}$ $\cdot 4 cm$
$S Q_{1}$ $=$ $\cos (56,30 °) \cdot 4 cm$
$S Q_{1}$ $\approx$ $2,22 cm$
Bemerkung: alternativ können wir auch im rechtwinkligen Dreieck $A M S$ den Wert von $A S$ mit dem Satz des Pythagoras als $\sqrt{3^{2} + 9^{2}} = \sqrt{90}$ berechnen. Dann verwenden wir den Sinussatz und erhalten den Sinus von $∡ A S C$ durch Auflösen von
$\frac{\sin ∡ A S C}{10} = \frac{\sin {52,15}^{°}}{\sqrt{90}}$
Berechnen Sie den Flächeninhalt $A$ des Dreiecks $P Q_{2} S$ .
Teilaufgabe d
Flächeninhalt $A$ des Dreiecks $P Q_{2} S$ :
$A_{D r e i e c k} = \frac{1}{2} \cdot S P \cdot P Q_{2} \cdot \sin (∡ Q_{2} P S)$
Uns fehlt also die Strecke $P Q_{2}$ und der Winkel $∡ Q_{2} P S$ :
Winkel $∡ Q_{2} P S$ :
Betrachten wir die Dreiecke $S P Q_{2}$ und $S A C$ , sehen wir, dass sie die gleiche Spitze haben, außerdem ist $P Q_{2} ∥ A C$ (zentrische Streckung), somit sind sie auch winkeltreu.
$∡ Q_{2} P S = ∡ C A S = 71,57 °$ wie in Teilaufgabe c) berechnet.
Strecke ${P Q}_{2}$ mit dem Sinussatz im Dreieck $S P Q_{2}$ :
$\frac{P S}{\sin (∡ S Q_{2} P)}$ $=$ $\frac{P Q_{2}}{\sin (∡ A S C)}$
$\frac{4 cm}{\sin (52,13 °)}$ $=$ $\frac{P Q_{2}}{\sin (56,30 °)}$ $\cdot \sin (56,30 °)$
$P Q_{2}$ $=$ $\frac{4 cm \cdot \sin (56,30 °)}{\sin (52,13 °)}$
$P Q_{2}$ $\approx$ $4,22 cm$
Nun können wir die Fläche $A$ berechnen:
$A_{D r e i e c k} = \frac{1}{2} \cdot S P \cdot P Q_{2} \cdot \sin (∡ Q_{2} P S) = \frac{1}{2} \cdot 4 cm \cdot 4,22 cm \cdot \sin (71,57 °) \approx 8,01 {cm}^{2}$
Im Dreieck $P Q_{3} S$ hat der Winkel $∢ Q_{3} P S$ das Maß $77 °$ . Der Punkt $Q_{3}$ ist die Spitze der Pyramide $A B C D Q_{3}$ mit dem Höhenfußpunkt $F_{3}$ und der Höhe $[F_{3} Q_{3}]$ .
Zeichnen Sie die Pyramide $A B C D Q_{3}$ mit der Höhe $[F_{3} Q_{3}]$ in das Schrägbild zu Teilaufgabe a) ein und berechnen Sie sodann die Länge der Strecke $[F_{3} Q_{3}]$ .
Teilaufgabe e
Zeichnung der Pyramide $A B C D Q_{3}$ :
$∡ Q_{3} P S = 77 °$
Der Schnittpunkt mit der Seite $[S C]$ bildet die Spitze der Pyramide $A B C D Q_{3}$ .
Verbinde nun alle Eckpunkte miteinander.
Fälle jetzt das Lot von $Q_{3}$ auf die Diagonale auf $[A C]$ , der Schnittpunkt ist der Fußpunkt $F$ der Höhe der Pyramide.
Länge der Höhe [ $Q_{3} F_{3}$ ] der Pyramide $A B C D Q_{3}$ im rechtwinkligen Dreieck $F_{3} C Q_{3}$ mit der Trigonometrie:
$\sin (∡ A C S) = \frac{Gegenkathete}{Hypotenuse} = \frac{Q_{3} F_{3}}{Q_{3} Q}$
Uns fehlt in dieser Formel die Seite $Q_{3} C$ . Aber: $Q_{3} C = S C - S Q_{3}$ .
Somit brauchen wir auch $S Q_{3}$ im Dreieck $S P Q_{3}$ mit dem Sinussatz:
$∡ S Q_{3} P = 180 ° - ∡ A S C - ∡ S P Q_{3} = 180 ° - 56,30 ° - 77 ° = 46,70 °$
$\frac{S P}{\sin (∡ S Q_{3} P)}$ $=$ $\frac{S Q_{3}}{\sin (∡ S P Q_{3})}$
$\frac{4 cm}{\sin (46,70 °)}$ $=$ $\frac{S Q_{3}}{\sin (77^{°})}$ $\cdot \sin (77 °)$
$S Q_{3}$ $=$ $\frac{4 cm \cdot \sin (77 °)}{\sin (46,70 °)}$
$S Q_{3}$ $=$ $5,36 cm$
$Q_{3} C = S C - S Q_{3} = 11,40 cm - 5,36 cm \approx 6,04 cm$
$\sin (∡ S C A) = \frac{Q_{3} F_{3}}{Q_{3} C}$
$\sin (52,13 °) = \frac{Q_{3} F_{3}}{6,04 cm}$
$Q_{3} F_{3_{}} = 6,04 cm \cdot \sin (52,13 °) \approx 4,77 cm$
Berechnen Sie das Volumen der Pyramiden $A B C D Q_{n}$ in Abhängigkeit von der Länge der Strecke $[S Q_{n}]$ mit $S Q_{n} (x) = x cm$ und $x \in ℝ$ ; $x \in] 0; 11,40 [.$
Teilaufgabe f
Volumen der Pyramiden $A B C D Q_{n}$ mit $S Q_{n} (x) = x$ :
$V_{A B C D Q_{n}} = \frac{1}{3} \cdot G_{D r a c h e} \cdot h$
Für die Höhe $h = Q_{n} F_{n}$ gehen wir wie oben vor:
$Q_{n} C = S C - S Q_{n} = 11,40 cm - x$
$\sin (∡ S C A)$ $=$ $\frac{Q_{n} F_{n}}{Q_{3} C}$
$\sin (52,13 °)$ $=$ $\frac{Q_{n} F_{n}}{11,40 cm - x}$
$Q_{n} F_{n}$ $=$ $\sin (52,13 °) (11,40 cm - x)$
$Q_{n} F_{n}$ $=$ $9,00 cm - \sin (52,13 °) \cdot x$
$Q_{n} F_{n}$ $=$ $9,00 cm - 0,79 x$
Für die Grundfläche $G = e \cdot f$ mit $e = B D = 8 cm$ und $f = A C = 10 cm$ :
$G_{D r a c h e} = \frac{1}{2} \cdot e \cdot f = \frac{1}{2} \cdot 8 \cdot 10 {cm}^{2} = 40 {cm}^{2}$
$V_{A B C D Q_{n}} (x) = \frac{1}{3} \cdot G_{D r a c h e} \cdot h = \frac{1}{3} \cdot 40 {cm}^{2} \cdot (9,00 cm - 0,79 x) = (120 - 10,53 x) {cm}^{3}$

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org

$\tan (∡ S C M)$	$=$	$\frac{Gegenkathete}{Ankathete}$
$\tan (∡ S C M)$	$=$	$\frac{M S}{M C}$
$\tan (∡ S C M)$	$=$	$\frac{9 cm}{(10 - 3) cm}$
$\tan (∡ S C M)$	$=$	$1, 285714$	$\tan^{- 1}$
$∡ S C M$	$\approx$	$52,13 °$

$\cos (∡ A S C)$	$=$	$\frac{Ankathete}{Hypotenuse}$
$\cos (∡ A S C)$	$=$	$\frac{S Q_{1}}{S P}$
$\cos (56,30 °)$	$=$	$\frac{S Q_{1}}{4 cm}$	$\cdot 4 cm$
$S Q_{1}$	$=$	$\cos (56,30 °) \cdot 4 cm$
$S Q_{1}$	$\approx$	$2,22 cm$

$\frac{P S}{\sin (∡ S Q_{2} P)}$	$=$	$\frac{P Q_{2}}{\sin (∡ A S C)}$
$\frac{4 cm}{\sin (52,13 °)}$	$=$	$\frac{P Q_{2}}{\sin (56,30 °)}$	$\cdot \sin (56,30 °)$
$P Q_{2}$	$=$	$\frac{4 cm \cdot \sin (56,30 °)}{\sin (52,13 °)}$
$P Q_{2}$	$\approx$	$4,22 cm$

$\frac{S P}{\sin (∡ S Q_{3} P)}$	$=$	$\frac{S Q_{3}}{\sin (∡ S P Q_{3})}$
$\frac{4 cm}{\sin (46,70 °)}$	$=$	$\frac{S Q_{3}}{\sin (77^{°})}$	$\cdot \sin (77 °)$
$S Q_{3}$	$=$	$\frac{4 cm \cdot \sin (77 °)}{\sin (46,70 °)}$
$S Q_{3}$	$=$	$5,36 cm$

$\sin (∡ S C A)$	$=$	$\frac{Q_{n} F_{n}}{Q_{3} C}$
$\sin (52,13 °)$	$=$	$\frac{Q_{n} F_{n}}{11,40 cm - x}$
$Q_{n} F_{n}$	$=$	$\sin (52,13 °) (11,40 cm - x)$
$Q_{n} F_{n}$	$=$	$9,00 cm - \sin (52,13 °) \cdot x$
$Q_{n} F_{n}$	$=$	$9,00 cm - 0,79 x$

Nachtermin Teil B

Teilaufgabe a

Teilaufgabe b

Teilaufgabe c

Teilaufgabe d

Teilaufgabe e

Teilaufgabe f