Geometrie, Teil B, Aufgabengruppe 1

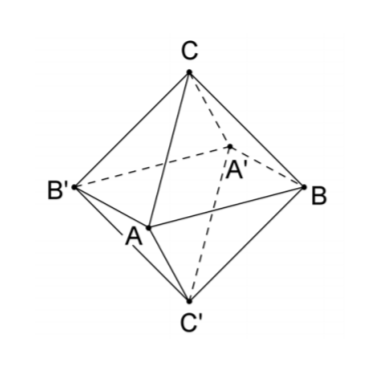
Lösung zur Teilaufgabe a)

Zwischenschritt: Gib die Ebene in Parameterform an

$A(6|3|3)$, $B(3|6|3)$, $C(3|3|6)$

Stelle zwei Richtungsvektoren der Ebene $E$ auf.

$\overrightarrow{AB}=\left(\begin{array}{c}3-6\\ 6-3\\ 3-3\end{array}\right)=\left(\begin{array}{c}-3\\ 3\\ 0\end{array}\right)$

$\overrightarrow{AC}=\left(\begin{array}{c}3-6\\ 3-3\\ 6-3\end{array}\right)=\left(\begin{array}{c}-3\\ 0\\ 3\end{array}\right)$

Schreibe (optional) in der Parameterform.

$E:\overrightarrow{X}=\overrightarrow{A}+\lambda \cdot \overrightarrow{AB}+\mu \cdot \overrightarrow{AC}$

$E:\overrightarrow{X}=\left(\begin{array}{c}6\\ 3\\ 3\end{array}\right)+\lambda \cdot \left(\begin{array}{c}-3\\ 3\\ 0\end{array}\right)+\mu \cdot \left(\begin{array}{c}-3\\ 0\\ 3\end{array}\right)$

Umrechnen in Normalenform

$\overrightarrow{AB}=\left(\begin{array}{c}-3\\ 3\\ 0\end{array}\right),\overrightarrow{AC}=\left(\begin{array}{c}-3\\ 0\\ 3\end{array}\right)$

Bilde das Vektorprodukt, um den Normalenvektor zu erhalten. Kürze soweit wie möglich.

$\left(\begin{array}{c}-3\\ 3\\ 0\end{array}\right)\times \left(\begin{array}{c}-3\\ 0\\ 3\end{array}\right)=\left(\begin{array}{c}9\\ 9\\ 9\end{array}\right)=9\cdot \left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)$$\Rightarrow \overrightarrow{n}=\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)$

Setze in die Vektordarstellung der Normalenform ein.

$E:\overrightarrow{n}\circ [\overrightarrow{X}-\overrightarrow{A}]=0$

$\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)\circ [\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)-\left(\begin{array}{c}6\\ 3\\ 3\end{array}\right)]=0$

Rechne aus.

$E:(x_1-6)+(x_2-3)+(x_3-3)=0$

$E:x_1+x_2+x_3-12=0$

Lösung zur Teilaufgabe b)

Lage der Ebene

Hinweis: Du musst zur Beantwortung dieser Frage nicht zwingend die Ebenengleichung aufstellen!

Möglichkeit 1: Über die Koordinaten

$A(6|3|3)$, $B(3|6|3)$, $Z(3|3|3)$

Schau dir die $x_3$-Koordinaten der drei Punkte an. Sie sind alle identisch, also auf gleicher Höhe! Sie befinden sich alle $3$ Einheiten über der $x_1,x_2$-Ebene.

Die Ebene muss somit parallel zur $x_1,x_2$-Ebene mit Abstand $3$ sein.

Möglichkeit 2: Über den Normalenvektor

$A(6|3|3)$, $B(3|6|3)$, $Z(3|3|3)$

Bilde zwei Richtungsvektoren aus den drei Punkten.

$\overrightarrow{AB}=\left(\begin{array}{c}-3\\ 3\\ 0\end{array}\right)$ , $\overrightarrow{AZ}=\left(\begin{array}{c}-3\\ 0\\ 0\end{array}\right)$

Bilde das Vektorprodukt.

$\overrightarrow{AB}\times \overrightarrow{AZ}=\left(\begin{array}{c}0\\ 0\\ 9\end{array}\right)$

Die $x_1$- und $x_2$-Koordinate des Normalenvektors sind 0. Die Ebene erstreckt sich deshalb nicht in $x_3$-Richtung. Sie ist parallel zur $x_1,x_2$-Ebene im Abstand $3$, da die $x_3$-Koordinate bei allen drei Punkten $3$ lautet.

$\overline{C^{\prime }C}$ senkrecht auf der Ebene durch $ABZ$

$\overrightarrow{C^{\prime }C}$ ist zweimal der Vektor $\overrightarrow{ZC}$, da $Z$ der Spiegelpunkt ist.

Also kann man statt du zeigen, dass $\overrightarrow{C^{\prime }C}$ senkrecht auf der Ebene steht, genauso gut zeigen, dass $\overrightarrow{ZC}$ senkrecht auf der Ebene steht, da sie beide die gleiche Richtung haben.

Stelle $\overrightarrow{ZC}$ auf.

$\overrightarrow{ZC}=\overrightarrow{C}-\overrightarrow{Z}=\left(\begin{array}{c}3\\ 3\\ 6\end{array}\right)-\left(\begin{array}{c}3\\ 3\\ 3\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ 3\end{array}\right)$

Vergleiche mit dem Normalenverktor der Ebene, denn dieser steht senkrecht auf $E$.

$-6\cdot \left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ -6\end{array}\right)$

Die Vektoren sind linear abhängig, deshalb steht $\overrightarrow{C{C}^{\prime }}$ senkrecht auf $E$.

Lösung zur Teilaufgabe c)

Bestimme $A^{\prime }$ und $B^{\prime }$

$A(6|3|3)$, $B(3|6|3),Z(3|3|3)$

Bilde die Vektoren $\overrightarrow{AZ}$ und $\overrightarrow{BZ}$.

$\overrightarrow{AZ}=\left(\begin{array}{c}-3\\ 0\\ 0\end{array}\right)$, $\overrightarrow{BZ}=\left(\begin{array}{c}0\\ -3\\ 0\end{array}\right)$

Um zu spiegeln, setze die Vektoren $\overrightarrow{AZ}$ und $\overrightarrow{BZ}$ an den Punkt $Z$.

$\overrightarrow{A^{\prime }}=\overrightarrow{Z}+\overrightarrow{AZ}=\left(\begin{array}{c}3\\ 3\\ 3\end{array}\right)+\left(\begin{array}{c}-3\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 3\\ 3\end{array}\right)$

$\overrightarrow{B^{\prime }}=\overrightarrow{Z}+\overrightarrow{BZ}=\left(\begin{array}{c}3\\ 3\\ 3\end{array}\right)+\left(\begin{array}{c}0\\ -3\\ 0\end{array}\right)=\left(\begin{array}{c}3\\ 0\\ 3\end{array}\right)$

Berechne die Seitenlängen des Quadrats

$A(6|3|3)$, $B(3|6|3)$

$A^{\prime }(0|3|3)$, $B^{\prime }(3|0|3)$

Ein Quadrat ist festgelegt durch zwei benachbarte, gleich lange Seiten und einen rechten Winkel zwischen diesen. Verwende $\overrightarrow{AB}$ und $\overrightarrow{A{B}^{\prime }}$.

$\overrightarrow{AB}=\left(\begin{array}{c}-3\\ 3\\ 0\end{array}\right)$

$\overrightarrow{A{B}^{\prime }}=\left(\begin{array}{c}3-6\\ 0-3\\ 3-3\end{array}\right)=\left(\begin{array}{c}-3\\ -3\\ 0\end{array}\right)$

Berechne die Längen der Vektoren.

$\begin{array}{rrl}\overline{AB}& =& \sqrt{(-3{)}^2+3^2+0^2}\\ & =& \sqrt{18}=3\sqrt{2}\\ \overline{A{B}^{\prime }}& =& \sqrt{(-3{)}^2+(-3{)}^2+0^2}\\ & =& \sqrt{18}=3\sqrt{2}\\ & & \end{array}$

Die Seiten sind gleich lang! Um auszuschließen, dass es sich nur um eine Raute aber nicht um ein Quadrat handelt, berechne den das Skalarprodukt zum Nachweis eines rechten Winkels.

$\begin{array}{rrl}\overrightarrow{AB}\circ \overrightarrow{A{B}^{\prime }}& =& 0\\ -3\cdot (-3)+3\cdot (-3)+0\cdot 0& =& 0\\ 0& =& 0\Rightarrow \overrightarrow{AB}⟂\overrightarrow{A{B}^{\prime }}\end{array}$

Somit ist $AB{A}^{\prime }{B}^{\prime }$ ein Quadrat.

Lösung zur Teilaufgabe d)

Bekannt

• $AB{A}^{\prime }{B}^{\prime }$ ist ein Quadrat mit Seitenlänge $3\sqrt{2}$.

• $Z$ ist der Mittelpunkt dieses Quadrats, da er das Spiegelzentrum ist.

• $\overline{ZC}$ ist die Höhe der Pyramide $AB{A}^{\prime }{B}^{\prime }C$.

Volumenformel einer Pyramide: $V=\frac{1}{3}Gh$

Berechne ihre Grundfläche.

$G=(3\sqrt{2}{)}^2=18$

Berechne die Höhe $\overline{ZC}$.

$\overrightarrow{ZC}=\left(\begin{array}{c}0\\ 0\\ 3\end{array}\right)$

Setze in die Formel ein.

$\overline{ZC}=\sqrt{0^2+0^2+3^2}=3$

$V=\frac{1}{3}\cdot 18\cdot 3=18$

Verdopple das Pyramidenvolumen, um das Volumen eines Oktaeders zu erhalten.

$V_{Oktaeder}=2\cdot 18=36$

Das Volumen des Oktaeders beträgt $36$.

Lösung zur Teilaufgabe e)

Die Dreiecke $ABC$ und $A{C}^{\prime }B$ liegen in eindeutig festgelegten Ebenen. Berechne den Winkel zwischen diesen beiden Ebenen.

Berechne die Normalenvektoren der Ebenen

Ebene $E$ durch $ABC$ aus Teilaufgabe a):

$E:x_1+x_2+x_3-12=0$

$\overrightarrow{n_E}=\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)$

Ebene $F$ durch $A{C}^{\prime }B$:

$A(6|3|3)$, $B(3|6|3)$, $C^{\prime }(3|3|0)$

Stelle die Vektoren $\overrightarrow{AB}$ und $\overrightarrow{A{C}^{\prime }}$ auf.

$\overrightarrow{AB}=\left(\begin{array}{c}3-6\\ 6-3\\ 3-3\end{array}\right)=\left(\begin{array}{c}-3\\ 3\\ 0\end{array}\right)$

$\overrightarrow{A{C}^{\prime }}=\left(\begin{array}{c}3-6\\ 3-3\\ 0-3\end{array}\right)=\left(\begin{array}{c}-3\\ 0\\ -3\end{array}\right)$

Bilde das Vektorprodukt.

$\begin{array}{rcl}\left(\begin{array}{c}-3\\ 3\\ 0\end{array}\right)& \times & \left(\begin{array}{c}-3\\ 0\\ -3\end{array}\right)\\ \left(\begin{array}{c}-9\\ -9\\ 9\end{array}\right)& =& -9\cdot \left(\begin{array}{c}1\\ 1\\ -1\end{array}\right)\\ \Rightarrow \overrightarrow{n_F}& =& \left(\begin{array}{c}-1\\ -1\\ 1\end{array}\right)\end{array}$

Berechne den Winkel mit

$cos(\alpha )=\frac{\overrightarrow{n_E}\circ \overrightarrow{n_F}}{|\overrightarrow{n_E}|\cdot |\overrightarrow{n_F}|}$.

$cos(\alpha )=\frac{1\cdot (-1)+1\cdot (-1)+1\cdot 1}{\sqrt{\phantom{(-1{)}^2}{1}^2+1^2+1^2}\cdot \sqrt{(-1{)}^2+(-1{)}^2+1^2}}=-\frac{1}{3}$

$\Rightarrow \alpha ={\mathrm{109,47}}^{\circ }$

Der Winkel beträgt also ${\mathrm{109,47}}^{\circ }$.

Lösung zur Teilaufgabe f)

Da $A^{\prime }$, $B^{\prime }$ und $C^{\prime }$ durch Spiegelung an $Z$ entstanden sind und $AB{A}^{\prime }{B}^{\prime }$ ein Quadrat ist, ist $Z$ der Mittelpunkt der Kugel.

Der Radius ist dann die Länge aller Vektoren, die von $Z$ ausgehen. Nehme zum Beispiel $\overrightarrow{ZC}$, von dem du bereits weißt, dass er $3LE$ lang ist.

Kugelgleichung

$Z(3|3|3)$, $r=3$

Stelle die Kugelgleichung auf.

$K:(x_1-m_1{)}^2+(x_2-m_2{)}^2+(x_3-m_3{)}^2=r^2$

$K:(x_1-3{)}^2+(x_2-3{)}^2+(x_3-3{)}^2=3^2$

Kugelvolumen

$r=3$

Setze in die Formel für das Kugelvolumen ein.

$V=\frac{4}{3}{r}^3\pi$ $V=\frac{4}{3}\cdot 3^3\pi$ $V=36\pi VE=\mathrm{113,10}VE$

Berechne den Anteil des Oktaedervolumens am Kugelvolumen

$\frac{36}{36\pi }=\frac{1}{\pi }\approx \mathrm{0,318}\approx \mathrm{31,8}\%$