Abiturkurs Geometrie

1 Übersicht

Inhalt des Kurses

Dieser Kurs soll dem Leser das zentrale Grundwissen, das für das bayrische Abitur relevant ist, vermitteln. Dabei werden alle zentrale Formeln und Sachverhalte kurz genannt und an Beispielen erklärt.

Falls gewisse Sachverhalte noch unklar sein sollten, gibt es Links zu ausführlicheren Erklärungen. Falls weitere Fragen offen bleiben, könnt ihr gerne die Kommentarfelder nutzen!

Vorkenntnisse

Das ist ein Überblickskurs, der eine kompakte Zusammenfassung für die Abiturvorbereitung bieten soll. Deshalb solltest du bereits die elfte und zwölfte Klasse besucht haben.

Kursdauer

Je nachdem, an wie viel du dich noch erinnern kannst, kann es kurz oder lang sein.

2 Vektoren

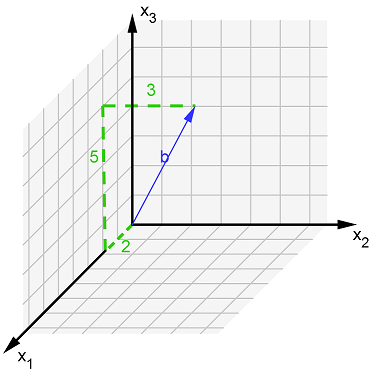
Ein Vektor $\vec{v} = (\begin{array}{c} x \\ y \\ z \end{array})$ gibt eine Richtung an. $x$ steht für die Anzahl Einheiten in $x_{1}$ -Richtung, $y$ in $x_{2}$ -Richtung und $z$ in $x_{3}$ -Richtung.

Ein Vektor hat im Gegensatz zu einem Punkt keinen festgelegten Ort. Will man allerdings einen Punkt als Vektor darstellen, verwendet man den Verbindungsvektor vom Ursprung zum Punkt. Diesen Vektor nennt man Ortsvektor.

Beispiel

Der Vektor $\vec{b}$ zeigt $2$ Einheiten in $x_{1}$ -Richtung, $3$ in $x_{2}$ -Richtung und $5$ in $x_{3}$ -Richtung.

Also lautet der Vektor:

$\vec{b} = (\begin{array}{c} 2 \\ 3 \\ 5 \end{array})$

Vektor von Punkt zu Punkt

Um den Vektor zwischen zwei Punkten zu berechnen, musst du "Spitze" minus "Fuß" rechnen:

Der Vektor von $A$ nach $B$ ist dann $\vec{A B} = \vec{B} - \vec{A} = (\begin{array}{c} x_{B} - x_{A} \\ y_{B} - y_{A} \\ z_{B} - z_{A} \end{array})$

Der Vektor $\vec{B A}$ von $B$ nach $A$ berechnet sich dementsprechend genau umgekehrt. Er zeigt damit auch genau in die entgegengesetzte Richtung.

3 Addition, Subtraktion, Multiplikation mit einem Skalar

Anschauung

Vektoren addiert man, indem man sie aneinanderhängt. Dabei setzt man den Fuß des einen Vektors an die Spitze des anderen.

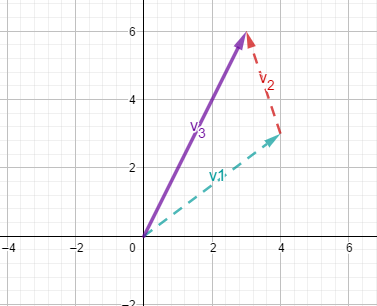
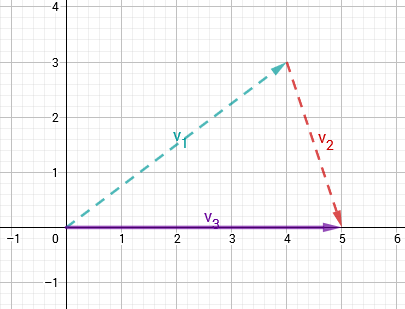
Vektoren subtrahiert man, indem man den umgedrehten Vektor des Subtrahenden zum Minuenden addiert.

Vektoren multipliziert man mit einem Skalar, indem man die Vektoren streckt (Skalar betragsmäßig größer 1), staucht (Skalar betragsmäßig kleiner 1) und evtl. umdreht (negativer Skalar).

Vorgehensweise

Vektoren addiert und subtrahiert man komponentenweise.

Auch bei der Multiplikation mit einem Skalar multipliziert man jede Komponente des Vektors mit dem Skalar.

Beispiele

Addition $(\begin{array}{c} 2 \\ 4 \\ 5 \end{array}) + (\begin{array}{c} 3 \\ 2 \\ 7 \end{array}) = (\begin{array}{c} 2 + 3 \\ 4 + 2 \\ 5 + 7 \end{array}) = (\begin{array}{c} 5 \\ 6 \\ 12 \end{array})$
Subtraktion $(\begin{array}{c} 6 \\ 3 \\ - 4 \end{array}) - (\begin{array}{c} 1 \\ - 7 \\ 2 \end{array}) = (\begin{array}{c} 6 - 1 \\ 3 - (- 7) \\ - 4 - 2 \end{array}) = (\begin{array}{c} 5 \\ 10 \\ - 6 \end{array})$
Multiplikation $2 \cdot (\begin{array}{c} 5 \\ - 3 \\ 7 \end{array}) = (\begin{array}{c} 2 \cdot 5 \\ 2 \cdot (- 3) \\ 2 \cdot 7 \end{array}) = (\begin{array}{c} 10 \\ - 6 \\ 14 \end{array})$

4 Betrag und Normierung

Betrag (Länge) von Vektoren

Der Betrag eines Vektors $\vec{v}$ ist anschaulich nichts anderes als seine Länge. Diese lässt sich wie folgt berechnen:

$| \vec{v} | = | (\begin{array}{c} x \\ y \\ z \end{array}) | = \sqrt{x^{2} + y^{2} + z^{2}}$

Normierung von Vektoren

Ein Vektor $\vec{v}$ heißt normiert, wenn sein Betrag (also seine Länge) $| \vec{v} | = 1$ ist. Der normierte Vektor wird auch als Einheitsvektor bezeichnet. Um einen Vektor zu normieren, müssen wir ihn durch seinen eigenen Betrag teilen:

$\vec{v_{0}} = \frac{\vec{v}}{| \vec{v} |}$

Ausnahme: Der Nullvektor lässt sich nicht normieren, da er die Länge $0$ hat.

Beispiel

Berechne zunächst die Länge des Vektors $(\begin{array}{c} 3 \\ 4 \end{array})$ und bilde anschließend den entsprechenden Einheitsvektor.

Länge

$| (\begin{array}{c} 3 \\ 4 \end{array}) | = \sqrt{3^{2} + 4^{2}} = 5$

Der Vektor $(\begin{array}{c} 3 \\ 4 \end{array})$ hat die Länge 5.

Normierung

$\frac{(\begin{array}{c} 3 \\ 4 \end{array})}{| (\begin{array}{c} 3 \\ 4 \end{array}) |} = \frac{(\begin{array}{c} 3 \\ 4 \end{array})}{5} = (\begin{array}{c} 3 \\ 4 \end{array}) \cdot \frac{1}{5} = (\begin{array}{c} \frac{3}{5} \\ \frac{4}{5} \end{array})$

Der Einheitsvektor zum Vektor $(\begin{array}{c} 3 \\ 4 \end{array})$ ist $(\begin{array}{c} \frac{3}{5} \\ \frac{4}{5} \end{array})$ .

5 Rechnen mit Vektoren

Laden

6 Lineare (Un)abhängigkeit (1/2)

Zwei Vektoren

Zwei Vektoren $\vec{a}$ und $\vec{b}$ nennt man linear abhängig, wenn der eine Vektor ein Vielfaches des anderen ist:

$\vec{a} = α \cdot \vec{b}$ oder $\vec{b} = β \cdot \vec{a}$

Ist das nicht der Fall, dann nennen wir die Vektoren linear unabhängig.

Bildlich kann man sich das so vorstellen:

Linear abhängig: Die Vektoren sind "parallel" (Sie müssen dafür nicht in die selbe Richtung zeigen, sondern können auch in genau entgegengesetzte Richtungen zeigen!)

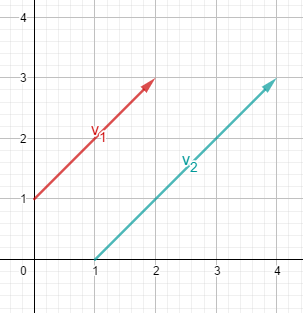
Linear unabhängig: Die Vektoren sind "nicht parallel"

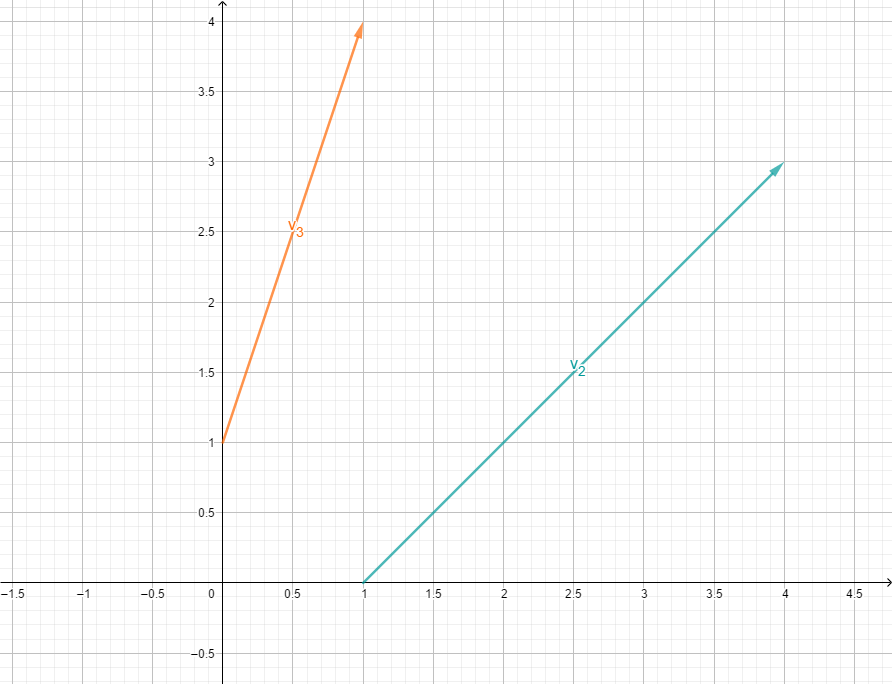
Beispiel 1

Geben sind folgende Vektoren:

$\vec{a} = (\begin{array}{c} 1 \\ 3 \\ 7 \end{array})$ und $\vec{b} = (\begin{array}{c} 3 \\ 9 \\ 21 \end{array})$

Jetzt versuchen wir eine passende Zahl n zu finden, mit der wir $\vec{a}$ multiplizieren, damit $\vec{b}$ rauskommt.

$n \cdot (\begin{array}{c} 1 \\ 3 \\ 7 \end{array}) = (\begin{array}{c} 3 \\ 9 \\ 21 \end{array})$

Wenn wir die x-Koordinate von $\vec{a}$ mit 3 multiplizieren, erhalten wir die passende x-Koordinate von $\vec{b}$ .

Jetzt prüfen wir noch, ob dies auch für die $y$ - und $z$ -Koordinaten gilt:

$y$ -Koordinate: $3 \cdot 3 = 9$

$z$ -Koordinate: $7 \cdot 3 = 21$

Wir stellen fest: stimmt! Also sind die beiden Vektoren linear abhängig.

Beispiel 2

Gegeben sind folgende Vektoren:

$\vec{a} = (\begin{array}{c} 3 \\ - 2 \\ 3 \end{array})$ und $\vec{b} = (\begin{array}{c} - 6 \\ 4 \\ - 9 \end{array})$

Wir versuchen wieder eine passende Zahl n zu finden, mit der $\vec{a}$ ein Vielfaches von $\vec{b}$ ist. Dafür gehen wir wieder Koordinatenweise vor:

Die x-Koordinate von $\vec{a}$ erhalten wir, indem wir die $x$ -Koordinate von $\vec{b}$ mit $(- \frac{1}{2})$ multiplizieren.

Dies gilt auch für die $y$ -Koordinate: $4 \cdot (- \frac{1}{2}) = - 2$

Dies gilt aber nicht für die $z$ -Koordinate: $(- 9) \cdot (- \frac{1}{2}) \neq 3$

Somit konnten wir keine passende Zahl finden und daher sind $\vec{a}$ und $\vec{b}$ linear unabhängig.

7 Lineare (Un)abhängigkeit (2/2)

Drei Vektoren

Drei Vektoren $\vec{a}$ , $\vec{b}$ und $\vec{c}$ sind linear abhängig, wenn man eine Linearkombination mit ihnen bilden kann, sodass der Nullvektor entsteht:

$(I) k_{1} \cdot \vec{a} + k_{2} \cdot \vec{b} + k_{3} \cdot \vec{c} = \vec{0}$

Dabei ist (mindestens) einer der Koeffizienten $k_{i}$ von $0$ verschieden.

Ist dagegen die Gleichung $(I)$ nur erfüllbar, wenn alle $k_{i}$ den Wert 0 annehmen, dann sind die Vektoren $\vec{a}$ , $\vec{b}$ und $\vec{c}$ linear unabhängig.

Bildliche Veranschaulichung:

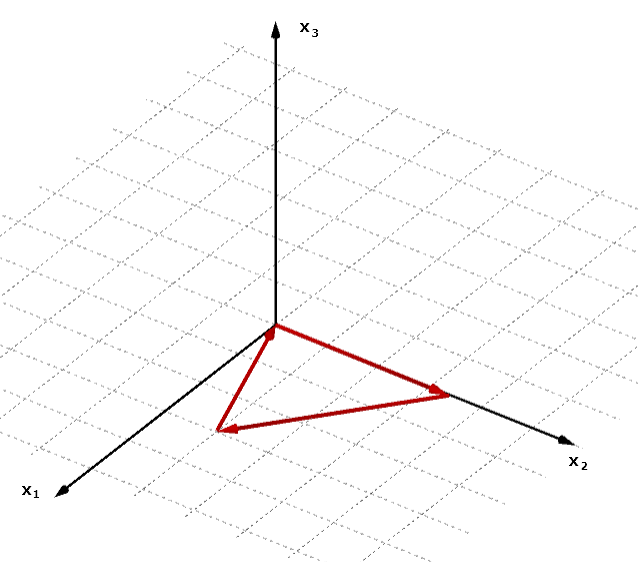
Linear abhängige Vektoren:

Die drei Vektoren liegen in einer Ebene.

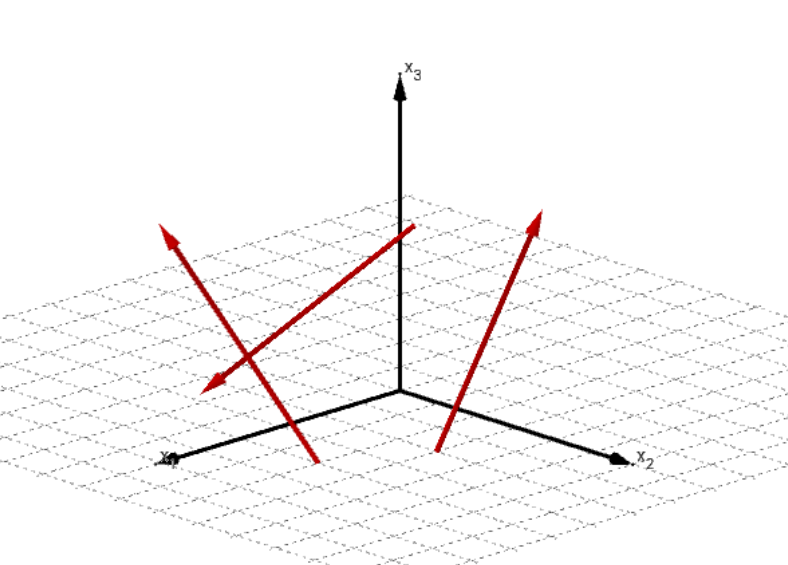
Linear unabhängige Vektoren:

Die drei Vektoren liegen nicht in einer Ebene.

Beispiel 1

Sind die drei Vektoren linear abhängig oder linear unabhängig?

$(\begin{array}{c} 1 \\ - 2 \\ 3 \end{array}), (\begin{array}{c} 1 \\ 2 \\ - 1 \end{array}) und (\begin{array}{c} 1 \\ 0 \\ 1 \end{array})$

Ansatz: Drei Vektoren sind linear abhängig, wenn man eine Linearkombination mit ihnen bilden kann, sodass der Nullvektor entsteht:

$k_{1} \cdot (\begin{array}{c} 1 \\ - 2 \\ 3 \end{array}) + k_{2} \cdot (\begin{array}{c} 1 \\ 2 \\ - 1 \end{array}) + k_{3} \cdot (\begin{array}{c} 1 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} 0 \\ 0 \\ 0 \end{array})$

Damit erhält man drei Gleichungen:

$\begin{array}{cccccccl} (I) : & k_{1} & + & k_{2} & + & k_{3} & = & 0 \\ (I I) : & - 2 k_{1} & + & 2 k_{2} & + & 0 & = & 0 \\ (I I I) : & 3 k_{1} & - & k_{2} & + & k_{3} & = & 0 \end{array}$

Aus $(I I) \Rightarrow k_{1} = k_{2}$ , eingesetzt in $(I) und (I I I)$ erhält man die Gleichungen:

$\begin{array}{cccccccl} (I^{'}) : & k_{1} & + & k_{1} & + & k_{3} & = & 0 & \Rightarrow & 2 k_{1} & + & k_{3} & = & 0 \\ (I I I^{'}) : & 3 k_{1} & - & k_{1} & + & k_{3} & = & 0 & \Rightarrow & 2 k_{1} & + & k_{3} & = & 0 \end{array}$

Rechnet man nun $(I^{'}) - (I I I^{'}) \Rightarrow 0 = 0$

Das ist eine wahre Aussage und bedeutet, dass das Gleichungssystem unendlich viele Lösungen hat. Die drei Vektoren sind damit linear abhängig.

Möchte man eine Lösung des Gleichungssystems angeben, so kann z.B. $k_{3} = 2$ gesetzt werden. Aus $(I^{'})$ folgt dann $k_{1} = - 1$ und aus $(I)$ folgt $k_{2} = - 1$ .

Beispiel 2

Sind die drei Vektoren linear abhängig oder linear unabhängig?

$(\begin{array}{c} 0 \\ 1 \\ 3 \end{array}), (\begin{array}{c} - 1 \\ 1 \\ 1 \end{array}) und (\begin{array}{c} 2 \\ 1 \\ 1 \end{array})$

Ansatz: Drei Vektoren sind linear abhängig, wenn man eine Linearkombination mit ihnen bilden kann, sodass der Nullvektor entsteht:

$k_{1} \cdot (\begin{array}{c} 0 \\ 1 \\ 3 \end{array}) + k_{2} \cdot (\begin{array}{c} - 1 \\ 1 \\ 1 \end{array}) + k_{3} \cdot (\begin{array}{c} 2 \\ 1 \\ 1 \end{array}) = (\begin{array}{c} 0 \\ 0 \\ 0 \end{array})$

Damit erhält man ein Gleichungssytem, das man z.B. mit den Additionsverfahren lösen kann:

$\begin{array}{cccccccl} (I) : & 0 & + & - k_{2} & + & 2 k_{3} & = & 0 \\ (I I) : & k_{1} & + & k_{2} & + & k_{3} & = & 0 \\ (I I I) : & 3 k_{1} & + & k_{2} & + & k_{3} & = & 0 \end{array}$

Man rechnet z.B. $(- 3) \cdot (I I) + (I I I) \Rightarrow (I^{'})$ und $(- 2) \cdot (I) \Rightarrow (I I^{'})$

$\begin{array}{cccccccl} (I^{'}) : & 0 & - & 2 k_{2} & - & 2 k_{3} & = & 0 \\ (I I^{'}) : & 0 & + & 2 k_{2} & - & 4 k_{3} & = & 0 \end{array}$

$(I^{'}) + (I I^{'}) : 0 k_{2} - 6 k_{3} = 0 \Rightarrow k_{3} = 0$

$k_{3} = 0$ eingesetzt in $(I) \Rightarrow k_{2} = 0$

$k_{3} = 0$ und $k_{2} = 0$ eingesetzt in $(I I) \Rightarrow k_{1} = 0$

Damit sind alle $k_{i} = 0$ , d.h. das Gleichungssystem hat nur die triviale Lösung.

Die drei Vektoren sind linear unabhängig.

8 Aufgaben zur linearen (Un)abhängigkeit

Laden

9 Skalarprodukt

Skalarprodukt

Das Skalarprodukt aus zwei Vektoren $\vec{a}$ und $\vec{b}$ ergibt eine Zahl s, einen sogenannten Skalar. Berechnet wird das Skalarprodukt, indem man komponentenweise multipliziert und anschließend addiert:

$\vec{a} \circ \vec{b} = (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}) \circ (\begin{array}{c} b_{1} \\ b_{2} \\ b_{3} \end{array}) = a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3} = s$

Man kann das Skalarprodukt aber auch unter Verwendung des Winkels $α$ , welcher zwischen den beiden Vektoren $\vec{v}$ und $\vec{w}$ liegt, berechnen:

\vec{v} \circ \vec{w} = | \vec{v} | \cdot | \vec{w} | \cdot \cos α

Wenn der Winkel $α = 90^{\circ}$ ist und somit die beiden Vektoren senkrecht zueinander sind, dann ergibt das Skalarprodukt 0:

\vec{v} \circ \vec{w} = | \vec{v} | \cdot | \vec{w} | \cdot \cos 90^{\circ} = | \vec{v} | \cdot | \vec{w} | \cdot 0 = 0

Willst du also überprüfen, ob zwei Vektoren senkrecht aufeinander stehen, berechnest du das Skalarprodukt.

Beispiel

Wir wollen überprüfen ob die Vektoren senkrecht aufeinander stehen.

Beispiel 1

$\vec{a} = (\begin{array}{c} 3 \\ - 4 \\ 1 \end{array})$ und $\vec{b} = (\begin{array}{c} 2 \\ 3 \\ 6 \end{array})$

Als erstes musst du das Skalarprodukt der beiden Vektoren berechnen.

$\vec{a} \circ \vec{b} = (\begin{array}{c} 3 \\ - 4 \\ 1 \end{array}) \circ (\begin{array}{c} 2 \\ 3 \\ 6 \end{array}) = 3 \cdot 2 + (- 4) \cdot 3 + 1 \cdot 6 = 6 - 12 + 6 = 0$

Das Skalarprodukt ist gleich $0$ , also stehen $\vec{a}$ und $\vec{b}$ senkrecht aufeinander.

Beispiel 2

$\vec{c} = (\begin{array}{c} 1 \\ 3 \\ 4 \end{array})$ und $\vec{d} = (\begin{array}{c} - 2 \\ 5 \\ 3 \end{array})$

Als erstes musst du das Skalarprodukt der beiden Vektoren berechnen.

$\vec{c} \circ \vec{d} = (\begin{array}{c} 1 \\ 3 \\ 4 \end{array}) \circ (\begin{array}{c} - 2 \\ 5 \\ 3 \end{array}) = 1 \cdot (- 2) + 3 \cdot 5 + 3 \cdot 4 = - 2 + 15 + 12 = 25$

Das Skalarprodukt ist 25 und somit stehen die Vektoren nicht senkrecht aufeinander.

10 Kreuzprodukt

Das Kreuzprodukt aus zwei Vektoren $\vec{a}$ und $\vec{b}$ ergibt einen neuen Vektor $\vec{w}$ , der gleichzeitig senkrecht auf den Vektoren $\vec{a}$ und $\vec{b}$ steht.

$\vec{a} \times \vec{b} = (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}) \times (\begin{array}{c} b_{1} \\ b_{2} \\ b_{3} \end{array}) = (\begin{array}{c} a_{2} b_{3} - a_{3} b_{2} \\ a_{3} b_{1} - a_{1} b_{3} \\ a_{1} b_{2} - a_{2} b_{1} \end{array}) = \vec{w}$

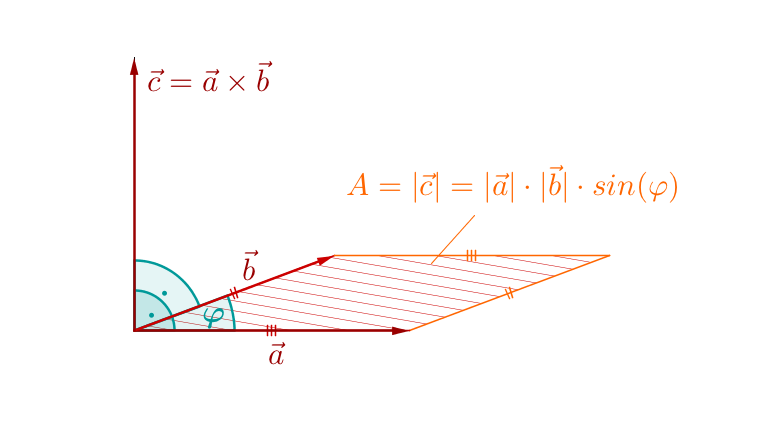
Der Betrag des berechneten Vektors $| \vec{w} |$ entspricht dem Flächeninhalt des von $\vec{a}$ und $\vec{b}$ aufgespannten Parallelogramms.

Achtung: Das Kreuzprodukt gibt es nur für 3-dimensionale Vektoren! Denn im 2-dimensionalen gibt es keinen Vektor, der senkrecht zu zwei anderen verschiedenen Vektoren stehen kann.

Beispiel

$(\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) \times (\begin{array}{c} 2 \\ - 3 \\ 4 \end{array}) = (\begin{array}{c} 2 \cdot 4 - 3 \cdot (- 3) \\ 3 \cdot 2 - 1 \cdot 4 \\ 1 \cdot (- 3) - 2 \cdot 2 \end{array}) = (\begin{array}{c} 17 \\ 2 \\ - 7 \end{array})$

11 Aufgaben zu Skalar und Kreuzprodukt

Berechne das Skalarprodukt der beiden Vektoren.

Laden

Prüfe, ob die beiden Vektoren senkrecht aufeinander stehen.

Laden

Berechne das Kreuzprodukt der beiden Vektoren.

Laden

Bestimme einen Vektor so, dass er senkrecht zu zwei gegebenen Vektoren ist.

Laden

12 Geraden

vektorielle Geradengleichung / Gleichung in Parameterform

Eine Gerade kann mit Hilfe von Vektoren beschrieben werden. Dafür benötigt man einen Aufpunkt $A$ und einen Richtungsvektor $\vec{v}$ .

Die Geradengleichung der Geraden $g$ sieht dann so aus:

$g : \vec{x} = \vec{O A} + λ \cdot \vec{v}$

wobei $\vec{O A}$ der Ortsvektor des Punktes $A$ ist.

Dabei spielt es keine Rolle ob die Vektoren 2- oder 3-dimensional sind. (Es funktioniert sogar mit n-dimensionalen Vektoren.)

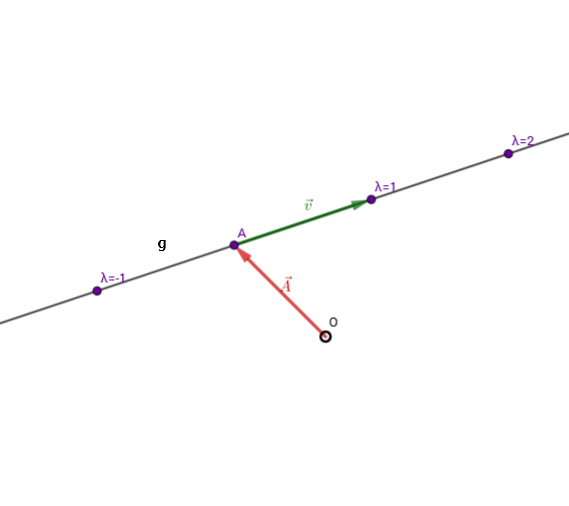
Geradengleichung aus 2 Punkten berechnen

Typischerweise bekommt man zwei verschiedene Punkte $A (a_{1} | a_{2})$ und $B (b_{1} | b_{2})$ .

Um die Geradengleichung zu bestimmen, die durch $A$ und $B$ geht, muss man sich zuerst aussuchen, welcher der beiden Punkte der Aufpunkt sein soll. Es spielt allerdings keine Rolle, ob man $A$ oder $B$ nimmt.

Anschließend bestimmen wir den Richtungsvektor $\vec{v}$ von $A$ nach $B$ , oder von $B$ nach $A$ , es spielt dabei ebenfalls keine Rolle welche Variante man wählt:

\vec{v} = \vec{O B} - \vec{O A} = (\begin{array}{c} b_{1} - a_{1} \\ b_{2} - a_{2} \end{array})

bzw.:

\vec{v} = \vec{O A} - \vec{O B} = (\begin{array}{c} a_{1} - b_{1} \\ a_{2} - b_{2} \end{array})

Jetzt müssen wir nur noch die Werte in unsere Geradengleichung von oben einsetzen. Weiter unten befinden sich ein Beispiel dazu.

Hinweis: Die Berechnung erfolgt, wie wir bereits wissen, analog für 3-dimensionale Vektoren.

Beispiel

Gegeben sind die Punkte $A (2 | 5 | - 3)$ und $B (7 | - 1 | - 12)$

Mit Aufpunkt $A$ ergibt sich folgende Geradengleichung:

\begin{aligned} g : \vec{x} & = \vec{O A} + λ \cdot \vec{v} \\ = \vec{O A} + λ \cdot \vec{A B} \\ = \vec{O A} + λ \cdot (\vec{O B} - \vec{O A}) \\ = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + λ \cdot [(\begin{array}{c} 7 \\ - 1 \\ - 12 \end{array}) - (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array})] \\ = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + λ \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) \end{aligned}

Mit Aufpunkt $B$ ergibt sich folgende Geradengleichung:

\begin{aligned} g : \vec{x} & = \vec{O B} + λ \cdot \vec{v} \\ = \vec{O B} + λ \cdot \vec{B A} \\ = \vec{O B} + λ \cdot (\vec{O A} - \vec{O B}) \\ = (\begin{array}{c} 7 \\ - 1 \\ - 12 \end{array}) + λ \cdot [(\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) - (\begin{array}{c} 7 \\ - 1 \\ - 12 \end{array})] \\ = (\begin{array}{c} 7 \\ - 1 \\ - 12 \end{array}) + λ \cdot (\begin{array}{c} - 5 \\ 6 \\ 9 \end{array}) \end{aligned}

13 Punkte auf der Geraden

Um Punkte zu erhalten, die auf der Geraden liegen, musst du Werte für $λ$ einsetzen. So kannst du mit dem passenden Wert jeden Punkt auf der Gerade erhalten.

Wenn du überprüfen willst, ob ein Punkt auf der Geraden liegt musst du zunächst den Punkt mit der Geradengleichung gleichsetzen. Anschließend stellst du ein Gleichungssystem auf und löst die einzelnen Gleichungen nach $λ$ auf. Kommt bei jeder Gleichung für $λ$ der gleiche Wert raus, liegt der Punkt auf der Geraden. In den anderen Fällen liegt er nicht auf der Geraden.

Verständlicher wird dies, wenn man sich ein Beispiel ansieht:

Beispiel

Gegeben ist die Geradengleichung:

$g : \vec{x} = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + λ \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array})$

Es soll nun geprüft werden, ob die Punkte a) $(7 | - 1 | - 12)$ und b) $(4 | 10 | - 6)$ auf der Geraden liegen.

Gleichungssystem aufstellen

$\begin{array}{llcr} I & 7 & = & 2 + 5 \cdot λ \\ II & - 1 & = & 5 - 6 \cdot λ \\ III & - 12 & = & - 3 - 9 \cdot λ \end{array}$

Werte von $λ$ berechnen.

$\begin{array}{llcr} I & λ & = & 1 \\ II & λ & = & 1 \\ III & λ & = & 1 \end{array}$

In allen Gleichungen hat $λ$ den gleichen Wert der Punkt liegt also auf der Geraden.

Punkt mit Geradengleichung gleichsetzen.

b) $(\begin{array}{c} 4 \\ 10 \\ - 6 \end{array}) = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + λ \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array})$

Gleichungssystem aufstellen.

\ $\begin{array}{llcr} I & 4 & = & 2 + 5 \cdot λ \\ II & 10 & = & 5 - 6 \cdot λ \\ III & - 6 & = & - 3 - 9 \cdot λ \end{array}$

Werte von $λ$ berechnen.

$\begin{array}{llcr} I & λ & = & \frac{2}{5} \\ II & λ & = & - \frac{5}{6} \\ III & λ & = & \frac{3}{9} \end{array}$

In den Gleichungen nimmt $λ$ unterschiedliche Werte an. Der Punkt liegt also nicht auf der Geraden.

14 Aufgaben zu Punkten auf Geraden

Laden

15 Gegenseitige Lage von Geraden und Geraden

Gerade und Gerade

Wenn man zwei Geraden im Raum betrachtet, gibt es 4 Möglichkeiten, wie sie zueinander stehen können:

Sie sind identisch (liegen "aufeinander")
Sie sind parallel
Sie schneiden sich
Sie sind windschief (schneiden sich nicht)

Wenn sich die beiden Geraden schneiden, kann man zusätzlich noch prüfen, ob sie orthogonal (rechtwinklig) zueinander sind.

Vorgehensweise

Wenn man prüfen möchte, wie zwei Geraden $g$ und $h$ zueinander stehen, geht man immer gleich vor.

Prüfe zuerst, ob die Richtungsvektoren beider Geraden linear unabhängig sind.

Beispiele

Um zu verdeutlichen, wie das Ganze genau funktionieren soll, folgt hier zu jeder Möglichkeit jeweils ein Beispiel zum Ausklappen

16 Aufgaben zur Lagebeziehung von Geraden

Bestimme die Lage der Geraden zueinander und berechne ihren Schnittpunkt wenn er exisitiert.

Laden

Weitere Aufgaben zu diesem Thema

17 Ebenen

Parameterform

Die Parameterform der Ebene E nutzt die bereits bekannte Form von Geraden aus und fügt einen weiteren Richtungsvektor hinzu. D.h. es gibt wieder einen Aufpunkt A und jetzt zwei Richtungsvektoren $\vec{u}$ und $\vec{v}$ :

$E : (\begin{array}{c} x \\ y \\ z \end{array}) = \vec{A} + λ_{1} \vec{u} + λ_{2} \vec{v} = \vec{A} + λ_{1} \cdot (\begin{array}{c} u_{1} \\ u_{2} \\ u_{3} \end{array}) + λ_{2} \cdot (\begin{array}{c} v_{1} \\ v_{2} \\ v_{3} \end{array})$

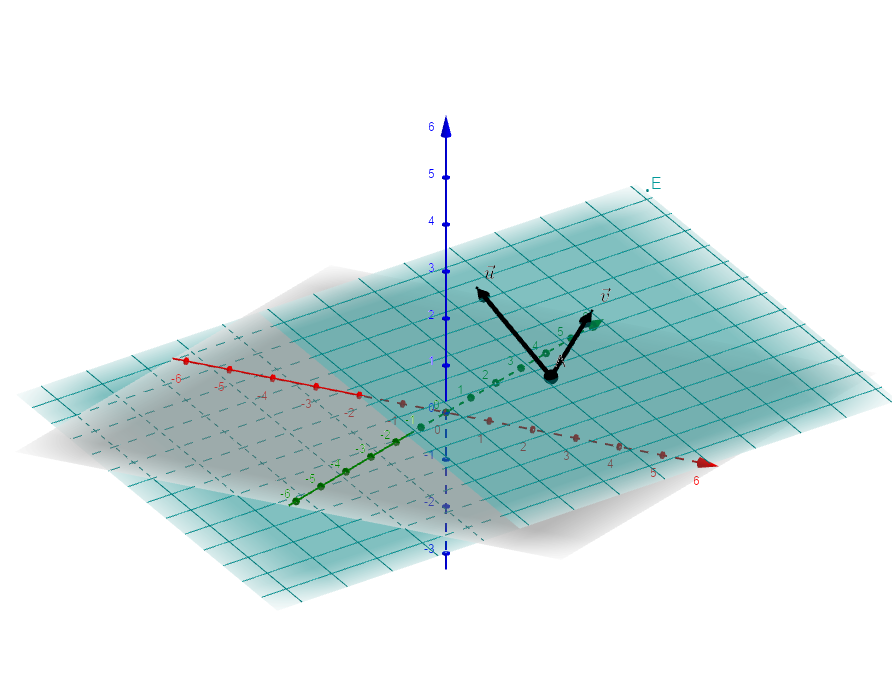
Koordinatenform

Eine Ebene E lässt sich auch durch die Verwendung der Koordinaten des kartesischen Koordinatensystems beschreiben. Die Ebene besteht dann aus denjenigen Punkten $(x, y, z)$ die folgende Gleichung erfüllen:

a x + b y + c z = d

Wobei a,b und c die Komponenten des Normalenvektors $\vec{n} = (\begin{array}{c} a \\ b \\ c \end{array})$ sind.

Der Abstand der Ebene vom Koordinatenursprung entspricht genau: $\frac{| d |}{| \vec{n} |}$ .

Ist der Normalenvektor normiert, entspricht der Abstand genau |d|.

Normalenform

Wenn man eine Ebene in Normalenform angeben will, benötigt man einen Punkt der Ebene (Aufpunkt $A$ ) und einen zur Ebene senkrechten Vektor $\vec{n}$ (Normalenvektor).

Ein Punkt $X$ (Ortsvektor $\vec{X}$ ) liegt in dieser Ebene, wenn der Vektor $\vec{A X}$ senkrecht auf dem Normalenvektor $\vec{n}$ steht.

Das Skalarprodukt von $\vec{A X}$ und $\vec{n}$ muss Null ergeben.

$E : \vec{n} \circ \vec{A X} = 0$

bzw.

$E : \vec{n} \circ (\vec{O X} - \vec{O A}) = 0$

Diese Gleichung heißt Normalenform der Ebene.

18 Hessesche Normalenform

Variante 1

Die Ebene ist in Koordinatenform gegeben.

Um die hessesche Normalenform dieser Ebene zu berechnen, teilt man die Ebenengleichung durch den Betrag des Normalenvektors.

Ebenengleichung in Koordinatenform:

E : a x_{1} + b x_{2} + c x_{3} = d

Normalenvektor dieser Ebene: $\vec{n} = (\begin{array}{c} a \\ b \\ c \end{array})$

Betrag des Normalenvektors: $| \vec{n} | = \sqrt{a^{2} + b^{2} + c^{2}}$

Dann ist die hessesche Normalenform:

E_{H N F} : \frac{\vec{x} \circ \vec{n} - d}{\sqrt{a^{2} + b^{2} + c^{2}}} = 0

(Der Kreis $\circ$ bezeichnet hier das Skalarprodukt.)

und man erhält ausmultipliziert:

E_{H N F} : \frac{a x_{1} + b x_{2} + c x_{3} - d}{| \vec{n} |} = \frac{a x_{1} + b x_{2} + c x_{3} - d}{\sqrt{a^{2} + b^{2} + c^{2}}} = 0

Beispiel Variante 1

Die Ebenengleichung in Koordinatenform der Ebene $E$ ist:

E : 3 x_{1} - 2 x_{2} + 6 x_{3} = 14

Der Normalenvektor der Ebene ist $\vec{n} = (\begin{array}{c} 3 \\ - 2 \\ 6 \end{array})$

Berechne den Betrag des Normalenvektors:

$\| \vec{n} \|$	$=$	$\sqrt{3^{2} + (- 2)^{2} + 6^{2}}$
	↓	Berechne die Quadrate.
	$=$	$\sqrt{9 + 4 + 36}$
	↓	Fasse zusammen.
	$=$	$\sqrt{49}$
	↓	Ziehe die Wurzel.
	$=$	$7$

Der Betrag des Normalenvektors ist $7$ .

$E_{H N F} : \frac{a x_{1} + b x_{2} + c x_{3} - d}{\| \vec{n} \|}$	$=$	$0$
	↓	Setze die Ebene $E : 3 x_{1} - 2 x_{2} + 6 x_{3} = 14$ und $\| \vec{n} \| = 7$ ein.
$\frac{3 x_{1} - 2 x_{2} + 6 x_{3} - 14}{7}$	$=$	$0$
	↓	Nach dem Distributivgesetz kann man aber auch jeden Summanden durch 7 teilen.
$\frac{3}{7} x_{1} - \frac{2}{7} x_{2} + \frac{6}{7} x_{3} - \frac{14}{7}$	$=$	$0$
	↓	Kürze.
$\frac{3}{7} x_{1} - \frac{2}{7} x_{2} + \frac{6}{7} x_{3} - 2$	$=$	$0$

Die hessesche Normalform der Ebene lautet:

E_{H N F} : \frac{3 x_{1} - 2 x_{2} + 6 x_{3} - 14}{7} = 0

oder

E_{H N F} : \frac{3}{7} x_{1} - \frac{2}{7} x_{2} + \frac{6}{7} x_{3} - 2 = 0

Variante 2

Die Ebene ist in Parameterform gegeben.

Um die hessesche Normalform dieser Ebene zu ermitteln, berechnet man den Normalenvektor $\vec{n}$ über das Kreuzprodukt der Richtungsvektoren und setzt ihn dann in die Gleichung ein:

E_{H N F} : \frac{\vec{n}}{| \vec{n} |} \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array})] = 0

Dabei ist $(\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array})$ der Ortsvektor eines (beliebigen) Punktes in der Ebene.

Beispiel Variante 2

Die Ebenengleichung in Parameterform der Ebene $E$ ist:

$E : \vec{X} = (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) + r \cdot (\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) + s \cdot (\begin{array}{c} 2 \\ 2 \\ 2 \end{array})$

Berechne das Kreuzprodukt der Richtungsvektoren:

$\vec{n} = (\begin{array}{c} 3 \\ 2 \\ 1 \end{array}) \times (\begin{array}{c} 2 \\ 2 \\ 2 \end{array}) = (\begin{array}{c} 2 \\ - 4 \\ 2 \end{array})$

Berechne den Betrag des Normalenvektors:

$\| \vec{n} \|$	$=$	$\sqrt{2^{2} + (- 4)^{2} + 2^{2}}$
	↓	Berechne die Quadrate.
	$=$	$\sqrt{4 + 16 + 4}$
	↓	Fasse zusammen.
	$=$	$\sqrt{24}$

Der Betrag des Normalenvektors ist $\sqrt{24}$ .

Setze in die Gleichung ein:

$E_{H N F} : \frac{\vec{n}}{\| \vec{n} \|} \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array})]$	$=$	$0$
	↓	Setze den Aufpunkt $(1 \| 2 \| 3)$ , $\vec{n} = (\begin{array}{c} 2 \\ - 4 \\ 2 \end{array})$ und $\| \vec{n} \| = \sqrt{24}$ ein.
$\frac{1}{\sqrt{24}} (\begin{array}{c} 2 \\ - 4 \\ 2 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})]$	$=$	$0$

Die hessesche Normalform der Ebene lautet:

E_{H N F} : \frac{1}{\sqrt{24}} (\begin{array}{c} 2 \\ - 4 \\ 2 \end{array}) \circ [(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}) - (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})] = 0

oder ausmultipliziert:

E_{H N F} : \frac{2 x_{1} - 4 x_{2} + 2 x_{3}}{\sqrt{24}} = 0

Hinweis: Auf der rechten Seite steht als Skalarprodukt des Normalenvektors und des Aufpunkts eine Null. Das bedeutet, dass die Ebene durch den Ursprung geht.

19 Parameterform umwandeln (1/2)

Parameterform in Normalenform umwandeln

Gegeben ist eine Ebenengleichung in Parameterform und man möchte diese jetzt in die Normalenform umwandeln.

Parameterform: $E : \vec{x} = (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}) + λ \cdot (\begin{array}{c} u_{1} \\ u_{2} \\ u_{2} \end{array}) + γ \cdot (\begin{array}{c} v_{1} \\ v_{2} \\ v_{3} \end{array})$

Normalenform: $\vec{n} \circ (\begin{array}{c} \vec{x} - \vec{A} \end{array}) = 0$

Zuerst berechnet man den Normalenvektor $\vec{n}$ über das Kreuzprodukt der beiden Richtungsvektoren unserer Ebene, da das Kreuzprodukt einen Vektor erzeugt, der rechtwinklig auf beiden Richtungsvektoren steht.

\vec{n} = (\begin{array}{c} u_{1} \\ u_{2} \\ u_{3} \end{array}) \times (\begin{array}{c} v_{1} \\ v_{2} \\ v_{3} \end{array}) = (\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array})

Die Reihenfolge spielt dabei keine Rolle, da diese nur die Orientierung des Normalenvektors umdreht.

Anschließend übernimmt man den Aufpunkt der Parameterform und setzt diesen für $\vec{A}$ in die Normalenform ein und man ist fertig.

(\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array}) \cdot (\begin{array}{c} \vec{x} - (\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array}) \end{array}) = 0

Beispiel:

Gegeben ist $E : \vec{x} = (\begin{array}{c} 2 \\ 1 \\ 1 \end{array}) + λ \cdot (\begin{array}{c} 1 \\ - 1 \\ 7 \end{array}) + γ \cdot (\begin{array}{c} 3 \\ 1 \\ 6 \end{array})$

Zuerst bestimmen wir den Normalenvektor mit dem Kreuzprodukt der Richtungsvektoren der Ebene:

\vec{n} = (\begin{array}{c} 1 \\ - 1 \\ 7 \end{array}) \times (\begin{array}{c} 3 \\ 1 \\ 6 \end{array}) = (\begin{array}{c} (- 1) \cdot 6 - 7 \cdot 1 \\ 7 \cdot 3 - 1 \cdot 6 \\ 1 \cdot 1 - (- 1) \cdot 3 \end{array}) = (\begin{array}{c} - 13 \\ 15 \\ 4 \end{array})

Anschließend setzt man den Aufpunkt und den Normalenvektor in die Standard-Normalenform ein:

(\begin{array}{c} - 13 \\ 15 \\ 4 \end{array}) \circ (\begin{array}{c} \vec{x} - (\begin{array}{c} 2 \\ 1 \\ 1 \end{array}) \end{array}) = 0

20 Parameterform umwandeln (2/2)

Parameterform in Koordinatenform umwandeln

Gegeben ist eine Ebenengleichung in Parameterform und man möchte diese jetzt in die Koordinatenform umwandeln.

Koordinatenform: $E : n_{1} x_{1} + n_{2} x_{2} + n_{3} x_{3} + n_{0} = 0$

Da die Koeffizienten $n_{1}, n_{2}, n_{3}$ vor den jeweiligen x-Werten die Einträge des Normalenvektors sind, berechnet man zuerst den Normalenvektor $\vec{n}$ . Diesen bekommt man durch das Kreuzprodukt aus den beiden Richtungsvektoren $\vec{u}$ und $\vec{v}$ :

$\vec{n} = \vec{u} \times \vec{v} = (\begin{array}{c} u_{1} \\ u_{2} \\ u_{3} \end{array}) \times (\begin{array}{c} v_{1} \\ v_{2} \\ v_{3} \end{array})$

Jetzt fehlt nur noch $n_{0}$ . Dafür setzt man den berechneten Normalenvektor $\vec{n}$ und den Aufpunkt $(\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \end{array})$ in die Standard-Koordinatenform ein und löst diese Gleichung nach $n_{0}$ auf. Tut man das erhält man:

n_{0} = - n_{1} x_{1} - n_{2} x_{2} - n_{3} x_{3}

Alle nötigen Werte sind jetzt bekannt und man kann die Ebene in Koordinatenform angeben.

Beispiel

Gegeben ist $E : \vec{x} = (\begin{array}{c} 2 \\ 1 \\ 1 \end{array}) + λ \cdot (\begin{array}{c} 1 \\ - 1 \\ 7 \end{array}) + γ \cdot (\begin{array}{c} 3 \\ 1 \\ 6 \end{array})$

Zuerst bestimmt man den Normalenvektor $\vec{n}$ mit dem Kreuzprodukt der Richtungsvektoren der Ebene: $\vec{n} = (\begin{array}{c} 1 \\ - 1 \\ 7 \end{array}) \times (\begin{array}{c} 3 \\ 1 \\ 6 \end{array}) = (\begin{array}{c} (- 1) \cdot 6 - 7 \cdot 1 \\ 7 \cdot 3 - 1 \cdot 6 \\ 1 \cdot 1 - (- 1) \cdot 3 \end{array}) = (\begin{array}{c} - 13 \\ 15 \\ 4 \end{array})$

Anschließend berechnet man $n_{0}$ , indem man den Aufpunkt $(\begin{array}{c} 2 \\ 1 \\ 1 \end{array})$ und den Normalenvektor $(\begin{array}{c} - 13 \\ 15 \\ 4 \end{array})$ in die Koordinatenform $E : n_{1} x_{1} + n_{2} x_{2} + n_{3} x_{3} + n_{0} = 0$ einsetzt und nach $n_{0}$ auflöst:

- 13 \cdot 2 + 15 \cdot 1 + 4 \cdot 1 + n_{0} = 0 ⟶ n_{0} = 13 \cdot 2 - 15 \cdot 1 - 4 \cdot 1 = 7

Somit erhält man folgende Ebene in Koordinatenform:

E : - 13 x_{1} + 15 x_{2} + 4 x_{3} + 7 = 0

21 Aufgaben zur Umwandlung der Parameterform

Laden

22 Punkte in der Ebene

Gegeben ist eine Ebene $E : \vec{X} = \vec{A} + r \cdot \vec{u} + s \cdot \vec{v}$ (Parameterform mit den Parametern $r, s \in ℝ$ ). Wenn man für r und s beliebige Werte einsetzt, erhält man einen Punkt in der Ebene.

Beispiel

Man betrachtet die Ebene $E : \vec{X} = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + r \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})$ und wählt z.B. für die beiden Parameter $r$ und $s$ die Werte $r = - 1$ und $s = 2$ . Diese beiden Werte beschreiben genau einen Punkt $P$ in der Ebene:

$\vec{P} = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + (- 1) \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + 2 \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array}) = (\begin{array}{c} - 1 \\ 15 \\ 12 \end{array})$

Der Punkt $P$ hat die Koordinaten: $P (- 1 | 15 | 12)$ und $P \in E$ .

Umgekehrt gibt es zu jedem Punkt in der Ebene passende Werte für die beiden Parameter $r$ und $s$ . Will man prüfen, ob ein Punkt $P$ in der Ebene liegt, wird der Ortvektor des Punktes $P$ mit der Ebenengleichung gleichgesetzt (man setzt für den Vektor $\vec{X}$ der Ebene den Ortvektor des Punktes $P$ ein).

Anschließend stellt man ein Gleichungssystem auf und löst die einzelnen Gleichungen nach $r$ und $s$ auf.

Verständlicher wird dies, wenn man sich Beispiele ansieht:

Beispiel 1

Gegeben ist die Ebenengleichung:

$E : \vec{X} = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + r \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})$

Es soll geprüft werden, ob der Punkt $P (7 | - 1 | - 12)$ in der Ebene liegt.

Lösung für Beispiel 1

Man setzt für den Vektor $\vec{X}$ der Ebene $E$ den Ortvektor des Punktes $P (7 | - 1 | - 12)$ ein:

$(\begin{array}{c} 7 \\ - 1 \\ - 12 \end{array}) = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + r \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})$

So erhält man ein Gleichungssystem mit drei Gleichungen und zwei Variablen.

$\begin{array}{llcr} (I) : & 7 & = & 2 + 5 \cdot r + 1 \cdot s \\ (I I) : & - 1 & = & 5 - 6 \cdot r + 2 \cdot s \\ (I I I) : & - 12 & = & - 3 - 9 \cdot r + 3 \cdot s \end{array}$

Umgeformt erhält man:

$\begin{array}{llcr} (I^{'}) : & 5 & = & 5 \cdot r + 1 \cdot s \\ (I I^{'}) : & - 6 & = & - 6 \cdot r + 2 \cdot s \\ (I I I^{'}) : & - 9 & = & - 9 \cdot r + 3 \cdot s \end{array}$

Um eine Variable zu eliminieren rechnet man z.B. $(- 2) \cdot (I^{'}) + (I I^{'})$

$\begin{array}{rrrrrcrr} (- 2) \cdot (I^{'}) : & - 10 & = & - 10 \cdot r & - & 2 \cdot s \\ + & (I I^{'}) : & - 6 & = & - 6 \cdot r & + & 2 \cdot s \\ - 16 & = & - 16 \cdot r & + & 0 \end{array}$

Also ist $r = 1$ .

Man setzt $r = 1$ in Gleichung $(I^{'}) : 5 = 5 \cdot r + 1 \cdot s$ ein:

$(I^{'}) : 5 = 5 \cdot 1 + 1 \cdot s \Rightarrow s = 0$

Mit den Werten $r = 1$ und $s = 0$ wird (als Probe) die Gleichung

$(I I^{'}) : - 6 = - 6 \cdot r + 2 \cdot s$ überprüft:

$(I I^{'}) : - 6 = - 6 \cdot 1 + 2 \cdot 0 ✓$ Somit wurden $r$ und $s$ richtig berechnet.

Mit den Werten $r = 1$ und $s = 0$ wird die Gleichung $(I I I^{'}) : - 9 = - 9 \cdot r + 3 \cdot s$ überprüft:

$(I I I^{'}) : - 9 = - 9 \cdot 1 + 3 \cdot 0 ✓$

Damit hat das Gleichungssystem eine eindeutige Lösung, d.h. der Punkt $P$ liegt in der Ebene.

Beispiel 2

Gegeben ist die Ebenengleichung:

$E : \vec{X} = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + r \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})$

Es soll geprüft werden, ob der Punkt $Q (4 | 10 | - 6)$ in der Ebene liegt.

Lösung für Beispiel 2

Man setzt für den Vektor $\vec{X}$ der Ebene $E$ den Ortvektor des Punktes $Q (4 | 10 | - 6)$ ein:

$(\begin{array}{c} 4 \\ 10 \\ - 6 \end{array}) = (\begin{array}{c} 2 \\ 5 \\ - 3 \end{array}) + r \cdot (\begin{array}{c} 5 \\ - 6 \\ - 9 \end{array}) + s \cdot (\begin{array}{c} 1 \\ 2 \\ 3 \end{array})$

So erhält man ein Gleichungssystem mit drei Gleichungen und zwei Variablen.

$\begin{array}{llcr} (I) : & 4 & = & 2 + 5 \cdot r + 1 \cdot s \\ (I I) : & 10 & = & 5 - 6 \cdot r + 2 \cdot s \\ (I I I) : & - 6 & = & - 3 - 9 \cdot r + 3 \cdot s \end{array}$

Umgeformt erhält man:

$\begin{array}{llcr} (I^{'}) : & 2 & = & 5 \cdot r + 1 \cdot s \\ (I I^{'}) : & 5 & = & - 6 \cdot r + 2 \cdot s \\ (I I I^{'}) : & - 3 & = & - 9 \cdot r + 3 \cdot s \end{array}$

Um eine Variable zu eliminieren rechnet man z.B. $(- 2) \cdot (I^{'}) + (I I^{'})$

$\begin{array}{rrrrrcrr} (- 2) \cdot (I^{'}) : & - 4 & = & - 10 \cdot r & - & 2 \cdot s \\ + & (I I^{'}) : & 5 & = & - 6 \cdot r & + & 2 \cdot s \\ 1 & = & - 16 \cdot r \end{array}$

Also ist $r = - \frac{1}{16}$ .

Man setzt $r = - \frac{1}{16}$ in Gleichung $(I^{'}) : 2 = 5 \cdot r + 1 \cdot s$ ein:

$(I^{'}) : 2 = 5 \cdot (- \frac{1}{16}) + 1 \cdot s \Rightarrow s = \frac{37}{16}$ .

Mit den Werten $r = - \frac{1}{16}$ und $s = \frac{37}{16}$ wird (als Probe) die Gleichung

$(I I^{'}) : 5 = - 6 \cdot r + 2 \cdot s$ überprüft:

$(I I^{'}) : 5 = - 6 \cdot (- \frac{1}{16}) + 2 \cdot \frac{37}{16} = \frac{6}{16} + \frac{74}{16} = \frac{80}{16} = 5 ✓$ Somit wurden $r$ und $s$ richtig berechnet.

Mit den Werten $r = - \frac{1}{16}$ und $s = \frac{37}{16}$ wird die Gleichung $(I I I^{'}) : - 3 = - 9 \cdot r + 3 \cdot s$ überprüft:

$(I I I^{'}) : - 3 = - 9 \cdot (- \frac{1}{16}) + 3 \cdot \frac{37}{16} = \frac{9}{16} + \frac{111}{16} = \frac{120}{16} = 7,5$

Gleichung $(I I I^{'})$ liefert ein falsches Ergebnis, da $- 3 \neq 7,5$ .

Das Gleichungssystem hat keine Lösung, d.h. der Punkt $Q$ liegt nicht in der Ebene.

23 Aufgaben zu Punkten in der Ebene

Laden

24 Gegenseitige Lage von Geraden und Ebenen

Wenn man eine Gerade und eine Ebene im Raum betrachtet, gibt es 3 verschiedene Möglichkeiten wie diese zueinander stehen können:

1. Die Gerade liegt in der Ebene.

2. Die Gerade ist echt parallel zur Ebene.

3. Die Gerade schneidet die Ebene in einem Punkt $S$ .

Vorgehensweise

Um die Lagebeziehung zwischen einer Geraden und einer Ebene zu bestimmen, ist es empfehlenswert wenn man eine Parametergleichung der Geraden und eine Koordinatengleichung der Ebene verwendet.

Gegeben sind eine Gerade $g : \vec{X} = \vec{A} + r \cdot \vec{u}$ und eine Ebene $E$ in Koordinatenform

$E : n_{1} x_{1} + n_{2} x_{2} + n_{3} x_{3} = n_{0}$ mit $\vec{n} = (\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array})$ .

1. Entscheidung über die gegenseitige Lage von $g$ und $E$

Man betrachtet das Skalarprodukt zwischen dem Normalenvektor $\vec{n}$ der Ebene $E$ und dem Richtungsvektor $\vec{u}$ der Geraden $g$ . Das folgende Diagramm erläutert die Entscheidungsfindung.

2. Schnittpunktsberechnung (für den Fall $\vec{n} \circ \vec{u} \neq 0$ )

Schritt 1: Die Geradengleichung wird in die Koordinatenform der Ebene eingesetzt:

Der allgemeine Geradenvektor hat die Koordinaten:

$x_{1} = A_{1} + r \cdot u_{1}$ ; $x_{2} = A_{2} + r \cdot u_{2}$ und $x_{3} = A_{3} + r \cdot u_{3}$

Durch Einsetzen dieser Terme in die Koordinatengleichung der Ebene $E : n_{1} x_{1} + n_{2} x_{2} + n_{3} x_{3} = n_{0}$ erhält man eine Gleichung für den Geradenparameter $r$ .

$n_{1} (A_{1} + r \cdot u_{1}) + n_{2} (A_{2} + r \cdot u_{2}) + n_{3} (A_{3} + r \cdot u_{3}) = n_{0}$

Schritt 2: Auflösung der Gleichung nach dem Parameter $r$

Man erhält für den Geradenparameter den Wert $r = r_{S}$ .

Dieser Wert $r_{S}$ wird in die Geradengleichung $g$ eingesetzt $\Rightarrow \vec{S} = \vec{A} + r_{S} \cdot \vec{u} = (\begin{array}{c} s_{1} \\ s_{2} \\ s_{3} \end{array})$ .

Die Gerade $g$ und die Ebene $E$ schneiden sich im Punkt $S (s_{1} | s_{2} | s_{3})$ .

Um zu verdeutlichen, wie das Ganze genau funktionieren soll, folgt hier zu jeder der drei möglichen Lagebeziehungen ein Beispiel zum Ausklappen.

Hier findet man weitere Aufgaben zur Lagebeziehung.

25 Aufgaben zur Lagebeziehung von Geraden und Ebenen

Laden

26 Gegenseitige Lage von Ebenen und Ebenen

Wenn man 2 Ebenen im Raum betrachtet, gibt es 3 verschiedene Möglichkeiten wie diese zueinander liegen können:

1. Die Ebenen sind identisch.

2. Die Ebenen sind (echt) parallel.

3. Die Ebenen schneiden sich (Schnittgerade).

Vorgehensweise

Um die Lagebeziehung zwischen zwei Ebenen zu bestimmen, ist es empfehlenswert, dass eine Ebene $E$ als Parametergleichung und die andere Ebene $F$ als Koordinatengleichung vorliegt.

Gegeben sind eine Ebene $E$ in Parameterform $E : \vec{X} = \vec{A} + r \cdot \vec{u} + s \cdot \vec{v}$ und eine Ebene $F$ in Koordinatenform

$F : n_{1} x_{1} + n_{2} x_{2} + n_{3} x_{3} = n_{0}$ mit $\vec{n} = (\begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array})$ .

1. Entscheidung über die gegenseitige Lage von $E$ und $F$

Man betrachtet die Skalarprodukte zwischen dem Normalenvektor $\vec{n}$ der Ebene $F$ und den beiden Richtungsvektoren $\vec{u}$ und $\vec{v}$ der Ebene $E$ . Man prüft, ob $\vec{n} \circ \vec{u} = 0$ und $\vec{n} \circ \vec{v} = 0$ ist. Sind beide Skalarprodukte gleich null, dann kann anhand der folgenden Graphik entschieden werden, wie die Ebenen zueinander liegen.

2. Schnittpunktsberechnung (für den Fall $\vec{n} \circ \vec{u} \neq 0$ )

Schritt 1: Die Ebenengleichung $E$ wird in die Koordinatenform der Ebene $F$ eingesetzt:

Der allgemeine Ebenenvektor von $E$ hat die Koordinaten:

$x_{1} = A_{1} + r \cdot u_{1} + s \cdot v_{1}$ ; $x_{2} = A_{2} + r \cdot u_{2} + s \cdot v_{2}$ und $x_{3} = A_{3} + r \cdot u_{3} + s \cdot v_{3}$

Durch Einsetzen dieser Terme in die Koordinatengleichung der Ebene

$F : n_{1} x_{1} + n_{2} x_{2} + n_{3} x_{3} = n_{0}$ erhält man eine Gleichung für die Ebenenparameter $r$ und s.

$n_{1} (A_{1} + r \cdot u_{1} + s \cdot v_{1}) + n_{2} (A_{2} + r \cdot u_{2} + s \cdot v_{2}) + n_{3} (A_{3} + r \cdot u_{3} + s \cdot v_{3}) = n_{0}$

Schritt 2: Auflösung der Gleichung nach einem der beiden Parameter

Beispiel 1: Man erhält eine Gleichung, die von einem der Parameter abhängt, also z.B. $r = 2 + s$ .

Die gefundene Gleichung wird in die Ebenengleichung $E$ eingesetzt und entsprechende Vektoren werden zusammengefasst $\Rightarrow g : \vec{X} = \vec{A} + (2 + s) \cdot \vec{u} + s \cdot \vec{v} = (\vec{A} + 2 \cdot \vec{u}) + s \cdot (\vec{u} + \vec{v})$

Beispiel 2: Man erhält eine Lösung für einen der beiden Parameter, also z.B. $r = 3$ .

Die gefundene Lösung $r = 3$ wird in die Ebenengleichung $E$ eingesetzt und entsprechende Vektoren werden zusammengefasst $\Rightarrow g : \vec{X} = (\vec{A} + 3 \cdot \vec{u}) + s \cdot \vec{v}$ .

Beispiel 3: Man erhält eine Lösung für den anderen Parameter, also z.B. $s = 0$ .

Die gefundene Lösung $s = 0$ wird in die Ebenengleichung $E$ eingesetzt

$\Rightarrow g : \vec{X} = \vec{A} + r \cdot \vec{u} + 0 \cdot \vec{v} = \vec{A} + r \cdot \vec{u}$ .

Die Ebene $E$ und die Ebene $F$ schneiden sich in der Geraden g.

Um zu verdeutlichen, wie das Ganze genau funktionieren soll, folgt hier zu jeder der drei Lagemöglichkeiten ein Beispiel zum Ausklappen.

Wenn die Ebenen nicht als Parameterform und Koordinatenform vorliegen, muss eventuell eine der Ebenen umgewandelt werden. (Die Vorgehensweise hierfür findet man auf den vorherigen Kursseiten.)

Weitere Aufgaben zu diesem Thema.

27 Aufgaben zur Lagebeziehung von Ebenen

Laden

Weitere Aufgaben zur Lagebeziehung von Ebenen.

28 Abstände zwischen Punkten

Einleitung

Wenn wir nun Punkte, Geraden und Ebenen im Raum betrachten, können wir auch die Abstände zwischen ihnen bestimmen. Dabei ist generell der kürzeste Abstand von Interesse.

Dafür sucht man meist zwei passende Punkte, zwischen denen man den Vektor und dessen Betrag bestimmen kann. Die gesuchten Punkte bekommen wir durch geschickte Wahl von Geraden, die wir durch die jeweiligen Objekte legen.

Den einfachsten Fall behandeln wir gleich vorweg:

Punkt und Punkt

Wir können bereits den Vektor zwischen zwei Punkten bestimmen und anschließend seinen Betrag ausrechnen. Der Betrag entspricht dann dem gesuchten Abstand.

Beispiel:

Gegeben sind zwei Punkte: $\vec{A} = (\begin{array}{c} - 3 \\ 4 \\ 3 \end{array})$ und $\vec{B} = (\begin{array}{c} 7 \\ - 3,5 \\ 1 \end{array})$

Wir berechnen den Vektor von $\vec{A}$ nach $\vec{B}$ (oder andersrum):

$\vec{A B} = \vec{B} - \vec{A} = (\begin{array}{c} 7 - (- 3) \\ - 3,5 - 4 \\ 1 - 3 \end{array}) = (\begin{array}{c} 10 \\ - 7,5 \\ - 2 \end{array})$

Als Letztes bestimmen wir den Betrag von $\vec{A B}$ :

$| \vec{A B} | = \sqrt{10^{2} + (- 7,5)^{2} + (- 2)^{2}} = \sqrt{100 + 56,25 + 4} = \sqrt{160,25} \approx 12,66$

Die beiden Punkte haben einen Abstand von etwa $12,66 LE$ voneinander.

29 Abstände zwischen Punkt und Gerade

Methode 1 Hilfsebene

1. Man erstellt eine Hilfsebene $H$ (in der Normalenform), die orthogonal (senkrecht) zur Geraden $g$ ist und den Punkt $P$ enthält. Dabei ist der Richtungsvektor der Geraden der Normalenvektor der Hilfsebene.

2. Man berechnet den Lotfußpunkt $F$ als Schnittpunkt der Geraden $g$ mit der Ebene $H$ .

3. Der gesuchte Abstand $d (P, F)$ ist die Länge des Lotvektors $| \vec{P F} |$ .

Beispiel für Methode 1

Laden

30 Abstände zwischen Punkten und Ebenen

Um den Abstand eines Punktes zur Ebene zu berechnen, braucht man die Ebene zunächst in der Hesseschen Normalform. Die Ebenengleichung muss also möglicherweise erst umgeformt werden. Durch Einsetzen des Punktes in die Ebenengleichung erhält man den Abstand des Punktes zur Ebene.

Methode 1: Hessische Normalenform

Gegeben ist die Ebene z.B. in Koordinatenform

$E : a x_{1} + b x_{2} + c x_{3} - d = 0$ und ein Punkt $P (P_{1} | P_{2} | P_{3})$ . Der Normalenvektor von $E$ ist:

$\vec{n} = (\begin{array}{c} a \\ b \\ c \end{array})$ und $| \vec{n} | = \sqrt{a^{2} + b^{2} + c^{2}}$

1. Man erstellt die Hessesche Normalenform:

$\begin{array}{l} E_{H N F} = \frac{a x_{1} + b x_{2} + c x_{3} - d}{| \vec{n} |} = 0 \\ E_{H N F} = \frac{a x_{1} + b x_{2} + c x_{3} - d}{\sqrt{a^{2} + b^{2} + c^{2}}} = 0 \end{array}$

2. Zur Berechnung des Abstandes setzt man die Koordinaten des Punktes $P$ in Hessesche Normalenform ein:

$d (P, E) = | \frac{a \cdot P_{1} + b \cdot P_{2} + c \cdot P_{3} - d}{\sqrt{a^{2} + b^{2} + c^{2}}} |$

Nachteil dieser Methode: Es kann nur der Abstand und nicht der Lotfußpunkt berechnet werden.

Beispiel für Methode 1

Laden

31 Abstände zwischen Geraden

Fall 1: Geraden sind parallel zueinander

Der Fall paralleler Geraden lässt sich auf die Abstandberechnung eines Punktes von einer Geraden zurückführen.

(siehe Abschnitt Punkt und Gerade:

Methode 1 Hilfsebene)

Beispiel 1

Laden

Fall 2: Geraden sind windschief

Gegeben sind die beiden Geraden

$g : \vec{O X} = \vec{O A} + r \cdot \vec{u}$ und $h : \vec{O X} = \vec{O B} + s \cdot \vec{v}$

Methode 1 Hessesche Normalenform

1. Bestimme eine Ebene $H$ , die die Gerade $h$ enthält und parallel zur Geraden $g$ ist.

Den Normalenvektor $\vec{n}$ dieser Ebenengleichung $H$ erhältst du, indem du das Kreuzprodukt der beiden Richtungsvektoren der Geraden $g$ und $h$ bildest.

(Alternativ ist die Bestimmung von $\vec{n}$ auch über das Skalarprodukt von $\vec{n} \circ \vec{u} = 0$ und $\vec{n} \circ \vec{v} = 0$ möglich.)

$\vec{n} = \vec{u} \times \vec{v}$

Mit diesem Normalenvektor erstellst du die Ebenengleichung in der Normalenform:

$H : \vec{n} \circ (\vec{O X} - \vec{O A}) = 0$

Für den Vektor $\vec{O A}$ setzt du den Aufpunkt $\vec{O B}$ der Geraden $h$ ein.

2. Schreibe die Normalenform der Ebene $H$ als Koordinatenform.

3. Berechne den Betrag des Normalenvektor $| \vec{n} |$ und wandle die Koordinatenform der Ebene in die Hessesche Normalenform um.

4. Den Abstand der beiden Geraden erhältst du, wenn du die Koordinaten des Aufpunktes der Geraden g in die Hessesche Normalenform einsetzt.

Windschiefe Geraden mit Hessescher Normalenform

Beispiel Methode 1

Laden

32 Abstände zwischen Geraden und Ebenen

Der Abstand einer zur Ebene $E$ (echt) parallelen Geraden $g$ wird mit zwei verschiedenen Methoden berechnet.

1. Lösung mit Hessescher Normalenform

2. Lösung mit einer Hilfsgeraden

Der Abstand $d$ zwischen Objekten im dreidimensionalen Raum ist definiert als die kürzeste Entfernung zwischen diesen Objekten.

Betrachtet man eine Gerade $g$ und eine Ebene $E$ , dann gibt es $3$ Lagebeziehungen dieser Objekte zueinander, verbunden mit entsprechenden gegenseitigen Abständen:

$g \in E$ , die Gerade liegt in der Ebene, $d (g, E) = 0$
$g \cap E = S$ , die Gerade schneidet die Ebene in einem Punkt $S$ , $d (g, E) = 0$
$g ∥ E$ , die Gerade ist (echt) parallel zu $E$ , dann ist der Abstand ungleich $0$ .

Für den letzten Fall wird die Abstandberechnung durchgeführt.

Vorgehensweise

Gegeben sind eine Ebenengleichung in Koordinatenform $E : a x_{1} + b x_{2} + c x_{3} - d = 0$ und eine zu $E$ parallele Gerade $g : \vec{X} = \vec{O P} + r \cdot \vec{u}$ . Berechne den Abstand der Geraden $g$ von der Ebene $E .$

1. Lösung mit Hessescher Normalenform

1. Erstelle von der Ebene $E$ die Hessesche Normalenform, indem du die Ebenengleichung mit $\frac{1}{| \vec{n} |} = \frac{1}{\sqrt{a^{2} + b^{2} + c^{2}}}$ multiplizierst.

$E_{H N F} : \frac{a x_{1} + b x_{2} + c x_{3} - d}{\sqrt{a^{2} + b^{2} + c^{2}}} = 0$

Der Abstand der Geraden zur Ebene kann durch den Abstand eines Punktes von der Geraden zur Ebene bestimmt werden. Dabei reicht ein beliebiger Punkt der Geraden zur Abstandbestimmung aus, da alle Geradenpunkte den gleichen Abstand zur Ebene haben. Wähle z.B. den Aufpunkt $P$ der Geraden.

2. Setze $P (p_{1} | p_{2} | p_{3})$ in $E_{H N F}$ ein:

$d (P, E) = | \frac{a \cdot p_{1} + b \cdot p_{2} + c \cdot p_{3} - d}{\sqrt{a^{2} + b^{2} + c^{2}}} |$

Der Abstand der Geraden $g$ zur Ebene $E$ ist gleich $d (P, E)$ .

Beispiel

Gegeben sind eine Ebenengleichung in Koordinatenform $E : 2 x_{1} + 2 x_{2} + x_{3} - 8 = 0$ und eine zu $E$ parallele Gerade $g : \vec{X} = (\begin{array}{c} 1 \\ 4 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 1 \\ 0 \\ - 2 \end{array})$ .

Berechne den Abstand der Geraden $g$ von der Ebene $E .$

Lösung

Erstelle von der Ebene $E$ die Hessesche Normalenform, indem du die Ebenengleichung mit $\frac{1}{| \vec{n} |}$ multiplizierst.

Der Normalenvektor der Ebene ist $\vec{n} = (\begin{array}{c} 2 \\ 2 \\ 1 \end{array})$ und sein Betrag ist:

$| \vec{n} | = \sqrt{2^{2} + 2^{2} + 1^{2}} = \sqrt{9} = 3$

Die Ebenengleichung muss also mit $\frac{1}{3}$ multipliziert werden.

$E_{H N F} : \frac{2 x + 2 y + z - 8}{3} = 0$

Berechne den Abstand der Geraden $g$ von der Ebene $E$ , indem du den Aufpunkt der Geraden $P (1 | 4 | 1)$ in $E_{H N F}$ einsetzt:

$d (P, E) = | \frac{2 \cdot 1 + 2 \cdot 4 + 1 \cdot 1 - 8}{3} | = | \frac{3}{3} | = 1$

Antwort: Der Abstand der Geraden $g$ zur Ebene $E$ beträgt $1 LE$ .

2. Lösung mit einer Hilfsgeraden

1. Stelle eine Hilfsgerade $h$ auf, die durch den Aufpunkt $P$ der Geraden $g$ verläuft und die orthogonal zur Ebene $E$ liegt. Der Normalenvektor der Ebene $E$ ist der Richtungsvektor der Hilfsgerade $h$ .

$h : \vec{X} = \vec{O P} + r \cdot \vec{n}$

2. Schneide die Hilfsgerade $h$ mit der Ebene $E$ . Setze dazu die Geradengleichung $h$ in die gegebene Ebenengleichung ein und löse die Gleichung nach dem Parameter $r$ auf.

3. Multipliziere den berechneten Parameter $r$ mit dem Normalenvektor $\vec{n}$ .

4. Berechne den Betrag des Vektors $r \cdot \vec{n}$ .

Der Abstand der Geraden $g$ zur Ebene $E$ ist: $d (g, E) = | r \cdot \vec{n} |$ .

Beispiel

Berechne den Abstand der Geraden $g$ von der Ebene $E .$

Lösung

Stelle eine Hilfsgerade $h$ auf, die durch den Aufpunkt $P$ der Geraden $g$ verläuft und die orthogonal zur Ebene $E$ liegt. Der Normalenvektor $\vec{n} = (\begin{array}{c} 2 \\ 2 \\ 1 \end{array})$ der Ebene $E$ ist der Richtungsvektor der Hilfsgeraden $h$ .

$h : \vec{X} = \vec{O P} + r \cdot \vec{n} = (\begin{array}{c} 1 \\ 4 \\ 1 \end{array}) + r \cdot (\begin{array}{c} 2 \\ 2 \\ 1 \end{array})$

Schneide die Hilfsgerade $h$ mit der Ebene $E$ . Setze dazu die Geradengleichung $h$ in die gegebene Ebenengleichung ein:

$2 x_{1} + 2 x_{2} + x_{3} - 8$	$=$	$0$
	↓	Setze $h$ in $E$ ein.
$2 \cdot (1 + 2 r) + 2 \cdot (4 + 2 r) + 1 \cdot (1 + r) - 8$	$=$	$0$
	↓	Löse die Klammern auf und fasse zusammen.
$2 + 4 r + 8 + 4 r + 1 + r - 8$	$=$	$0$
$3 + 9 r$	$=$	$0$	$- 3$
$9 r$	$=$	$- 3$	$: 9$
$r$	$=$	$- \frac{3}{9}$
	↓	Kürze.
$r$	$=$	$- \frac{1}{3}$

Multipliziere den berechneten Parameter $r = - \frac{1}{3}$ mit dem Normalenvektor $\vec{n} = (\begin{array}{c} 2 \\ 2 \\ 1 \end{array})$ und berechne den Betrag des Vektors $r \cdot \vec{n}$ .

$d (g, E) = | (- \frac{1}{3}) \cdot (\begin{array}{c} 2 \\ 2 \\ 1 \end{array}) | = | - \frac{1}{3} | | (\begin{array}{c} 2 \\ 2 \\ 1 \end{array}) | = \frac{1}{3} \sqrt{2^{2} + 2^{2} + 1} = \frac{1}{3} \cdot 3 = 1$

Antwort: Der Abstand der Geraden $g$ zur Ebene $E$ beträgt $1 LE$ .

33 Abstände zwischen Ebenen

Ebene und Ebene

Methode 1: Hessesche Normalenform

Die beiden Ebenen $E_{1}$ und $E_{2}$ sind parallel. Dann berechnet man den Abstand dieser beiden Ebenen, indem ein Punkt der Ebene $E_{2}$ in die Hessesche Normalenform der Ebene $E_{1}$ eingesetzt wird. Das Verfahren entspricht dann der "Berechnung des Abstandes eines Punktes zur Ebene ".

Beispiel

Laden

34 Winkel zwischen Vektoren, Geraden und Ebenen

Winkel zwischen zwei Vektoren

Der Winkel $α$ zwischen zwei Vektoren $\vec{a}$ und $\vec{b}$ berechnet sich aus dem Quotienten des Skalarprodukts und dem Produkt aus den Beträgen (Längen) von $\vec{a}$ und $\vec{b}$ .

\cos α = \frac{\vec{a} \cdot \vec{b}}{| \vec{a} | \cdot | \vec{b} |}

Der Winkel zwischen zwei Vektoren kann Werte zwischen 0° und 180° annehmen.

Winkel zwischen zwei Geraden

Der Schnittwinkel $ϕ$ zwischen zwei Geraden entspricht dem Winkel zwischen den jeweiligen Richtungsvektoren $\vec{a}$ und $\vec{b}$ . Jedoch haben Geraden höchstens einen Schnittwinkel zwischen 0° und 90°. Diesen Wertebereich erreicht man, wenn man im Zähler den Absolutbetrag des Skalarproduktes nimmt.

\cos ϕ = \frac{| \vec{a} \cdot \vec{b} |}{| \vec{a} | \cdot | \vec{b} |}

Bemerkung: Im Zähler und Nenner sind verschiedene Beträge gemeint. Im Zähler ist es der Betrag einer Zahl (eines Skalars) und im Nenner der Betrag eines Vektors, also seine Länge.

Winkel zwischen zwei Ebenen

Der Schnittwinkel $ϕ$ zwischen zwei Ebenen entspricht dem Winkel zwischen den beiden Normalenvektoren ${\vec{n}}_{1}$ und ${\vec{n}}_{2}$ . Die Berechnung ist dann wieder wie bei den Geraden:

\cos ϕ = \frac{| {\vec{n}}_{1} \cdot {\vec{n}}_{2} |}{| {\vec{n}}_{1} | \cdot | {\vec{n}}_{2} |}

Winkel zwischen Gerade und Ebene

Diesmal verwendet man den Richtungsvektor $\vec{a}$ der Gerade und den Normalenvektor der Ebene $\vec{n}$ .

1. Methode:

Da man den Normalenvektor der Ebene verwendet und dieser um 90° gedreht zur Ebene liegt, müssen wir den entstehenden Winkel anpassen:

\cos ϕ = \frac{| \vec{a} \cdot \vec{n} |}{| \vec{a} | \cdot | \vec{n} |}

Der gesuchte Winkel $β$ zwischen Gerade und Ebene ist dann:

β = 90^{\circ} - ϕ

2. Methode:

Da die Sinus- und Kosinusfunktion auch um 90° verschoben sind, kann man $β$ auch direkt berechnen:

\sin β = \frac{| \vec{a} \cdot \vec{n} |}{| \vec{a} | \cdot | \vec{n} |}

35 Flächen berechnen

Fläche über Kreuzprodukt

Die Fläche, die zwei Vektoren $\vec{a}$ und $\vec{b}$ aufspannen, lässt sich über das Kreuzprodukt berechnen. Die Länge bzw. der Betrag des entstehenden Vektors entspricht dem Flächeninhalt des aufgespannten Parallelogramms.

A_{P a r a l l e l o g r a m m} = | \vec{a} \times \vec{b} |

Quadrat und Rechteck

Da Quadrate und Rechtecke Spezialfälle eines Parallelogramms sind, berechnet man diese auch über das Kreuzprodukt.

Dreieck

Die Fläche eines Dreiecks entspricht der Hälfte der Fläche des aufgespannten Parallelogramms

A_{D r e i c e k} = \frac{1}{2} \cdot | \vec{a} \times \vec{b} |

(Trapez)

Das Trapez lässt sich nicht direkt über das Kreuzprodukt berechnen. Daher ist es ratsam einfach die bekannte Formel zu verwenden und die Längen über die Vektorbeträge zu beschaffen.

A_{T r a p e z} = \frac{1}{2} \cdot (| \vec{a} | + | \vec{c} |) \cdot | \vec{h} |

36 Volumen berechnen

Man darf nicht vergessen, dass man Volumina auch über die bereits bekannten Volumenformeln berechnen kann. Die nötigen Längen sind dann einfach die Beträge der entsprechenden Vektoren.

Dennoch gibt es eine Möglichkeit Volumina über das sog. Spatprodukt zu berechnen.

Spat

Der Körper, den drei Vektoren $\vec{a}, \vec{b}$ und $\vec{c}$ aufspannen, heißt Spat. Man berechnet das Volumen eines Spates über das Spatprodukt. Das Spatprodukt ist nichts Neues, sondern nur eine Kombination aus Kreuz- und Skalarprodukt.

V_{S p a t} = | \vec{a} \circ (\vec{b} \times \vec{c}) |

Würfel und Quader

Da Würfel und Quader Spezialfälle eines Spates sind, gilt hier die selbe Berechnung wie oben.

Zylinder

Hier gilt die bereits bekannte Formel: Grundfläche mal Höhe. Die nötigen Größen können ggf. wieder über die Vektorbeträge ausgerechnet werden.

Pyramide

Das Volumen einer dreiseitigen Pyramide ABCD berechnet sich wie folgt:

V_{P y r a m i d e} = \frac{1}{6} \cdot | \vec{A B} \circ (\vec{A C} \times \vec{A D}) |

37 Aufgaben zum Üben

Am besten versuchst du jetzt die alten Originalprüfungsaufgaben aus den letzten Jahren zu rechnen.

Hier findet man Aufgaben aus dem bayerischen Abitur.

Hier findet man Aufgaben aus dem bayerischen FOS & BOS.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

Abiturkurs Geometrie

1 Übersicht

Inhalt des Kurses

Vorkenntnisse

Kursdauer

2 Vektoren

Beispiel

Vektor von Punkt zu Punkt

3 Addition, Subtraktion, Multiplikation mit einem Skalar

Anschauung

Vorgehensweise

Beispiele

4 Betrag und Normierung

Betrag (Länge) von Vektoren

Normierung von Vektoren

Beispiel

5 Rechnen mit Vektoren

6 Lineare (Un)abhängigkeit (1/2)

Zwei Vektoren

Beispiel 1

Beispiel 2

7 Lineare (Un)abhängigkeit (2/2)

Drei Vektoren

Beispiel 1

Beispiel 2

8 Aufgaben zur linearen (Un)abhängigkeit

9 Skalarprodukt

Skalarprodukt

Beispiel

10 Kreuzprodukt

Beispiel

11 Aufgaben zu Skalar und Kreuzprodukt

12 Geraden

vektorielle Geradengleichung / Gleichung in Parameterform

Geradengleichung aus 2 Punkten berechnen

Beispiel

13 Punkte auf der Geraden

Beispiel

14 Aufgaben zu Punkten auf Geraden

15 Gegenseitige Lage von Geraden und Geraden

Gerade und Gerade

Vorgehensweise

Beispiele

16 Aufgaben zur Lagebeziehung von Geraden

17 Ebenen

Parameterform

Koordinatenform

Normalenform

18 Hessesche Normalenform

Variante 1

Beispiel Variante 1

Variante 2

Beispiel Variante 2

19 Parameterform umwandeln (1/2)

Parameterform in Normalenform umwandeln

Beispiel:

20 Parameterform umwandeln (2/2)

Parameterform in Koordinatenform umwandeln

Beispiel

21 Aufgaben zur Umwandlung der Parameterform

22 Punkte in der Ebene

Beispiel

Beispiel 1

Lösung für Beispiel 1

Beispiel 2

Lösung für Beispiel 2

23 Aufgaben zu Punkten in der Ebene

24 Gegenseitige Lage von Geraden und Ebenen

Vorgehensweise

Um die Lagebeziehung zwischen einer Geraden und einer Ebene zu bestimmen, ist es empfehlenswert wenn man eine Parametergleichung der Geraden und eine Koordinatengleichung der Ebene verwendet.

1. Entscheidung über die gegenseitige Lage von g und E

2. Schnittpunktsberechnung (für den Fall n→∘u→≠0 )

Schritt 1: Die Geradengleichung wird in die Koordinatenform der Ebene eingesetzt:

Der allgemeine Geradenvektor hat die Koordinaten:

x1=A1+r⋅u1; x2=A2+r⋅u2 und x3=A3+r⋅u3

Durch Einsetzen dieser Terme in die Koordinatengleichung der Ebene E:n1x1+n2x2+n3x3=n0 erhält man eine Gleichung für den Geradenparameter r.

n1(A1+r⋅u1)+n2(A2+r⋅u2)+n3(A3+r⋅u3)=n0

Schritt 2: Auflösung der Gleichung nach dem Parameter r

Man erhält für den Geradenparameter den Wert r=rS.

Dieser Wert rS wird in die Geradengleichung g eingesetzt ⇒S→=A→+rS⋅u→=(s1s2s3).

1. Entscheidung über die gegenseitige Lage von $g$ und $E$

2. Schnittpunktsberechnung (für den Fall $\vec{n} \circ \vec{u} \neq 0$ )

$x_{1} = A_{1} + r \cdot u_{1}$ ; $x_{2} = A_{2} + r \cdot u_{2}$ und $x_{3} = A_{3} + r \cdot u_{3}$

Durch Einsetzen dieser Terme in die Koordinatengleichung der Ebene $E : n_{1} x_{1} + n_{2} x_{2} + n_{3} x_{3} = n_{0}$ erhält man eine Gleichung für den Geradenparameter $r$ .

$n_{1} (A_{1} + r \cdot u_{1}) + n_{2} (A_{2} + r \cdot u_{2}) + n_{3} (A_{3} + r \cdot u_{3}) = n_{0}$

Schritt 2: Auflösung der Gleichung nach dem Parameter $r$

Man erhält für den Geradenparameter den Wert $r = r_{S}$ .

Dieser Wert $r_{S}$ wird in die Geradengleichung $g$ eingesetzt $\Rightarrow \vec{S} = \vec{A} + r_{S} \cdot \vec{u} = (\begin{array}{c} s_{1} \\ s_{2} \\ s_{3} \end{array})$ .

Die Gerade $g$ und die Ebene $E$ schneiden sich im Punkt $S (s_{1} | s_{2} | s_{3})$ .

1. Entscheidung über die gegenseitige Lage von $E$ und $F$

2. Schnittpunktsberechnung (für den Fall $\vec{n} \circ \vec{u} \neq 0$ )

Schritt 1: Die Ebenengleichung $E$ wird in die Koordinatenform der Ebene $F$ eingesetzt:

Der allgemeine Ebenenvektor von $E$ hat die Koordinaten:

$x_{1} = A_{1} + r \cdot u_{1} + s \cdot v_{1}$ ; $x_{2} = A_{2} + r \cdot u_{2} + s \cdot v_{2}$ und $x_{3} = A_{3} + r \cdot u_{3} + s \cdot v_{3}$

$F : n_{1} x_{1} + n_{2} x_{2} + n_{3} x_{3} = n_{0}$ erhält man eine Gleichung für die Ebenenparameter $r$ und s.

$n_{1} (A_{1} + r \cdot u_{1} + s \cdot v_{1}) + n_{2} (A_{2} + r \cdot u_{2} + s \cdot v_{2}) + n_{3} (A_{3} + r \cdot u_{3} + s \cdot v_{3}) = n_{0}$

Die gefundene Gleichung wird in die Ebenengleichung $E$ eingesetzt und entsprechende Vektoren werden zusammengefasst $\Rightarrow g : \vec{X} = \vec{A} + (2 + s) \cdot \vec{u} + s \cdot \vec{v} = (\vec{A} + 2 \cdot \vec{u}) + s \cdot (\vec{u} + \vec{v})$

Die gefundene Lösung $r = 3$ wird in die Ebenengleichung $E$ eingesetzt und entsprechende Vektoren werden zusammengefasst $\Rightarrow g : \vec{X} = (\vec{A} + 3 \cdot \vec{u}) + s \cdot \vec{v}$ .

Die gefundene Lösung $s = 0$ wird in die Ebenengleichung $E$ eingesetzt

$\Rightarrow g : \vec{X} = \vec{A} + r \cdot \vec{u} + 0 \cdot \vec{v} = \vec{A} + r \cdot \vec{u}$ .

Die Ebene $E$ und die Ebene $F$ schneiden sich in der Geraden g.