Aufgaben zu Drachenviereck und Raute
Hier findest du Rechenaufgaben zum Drachenviereck und der Raute. Lerne, wichtige Größen zu berechnen und vertiefe dein Wissen!
- 1
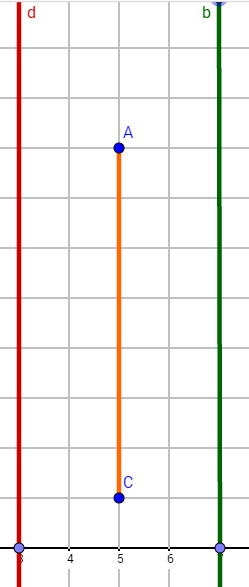
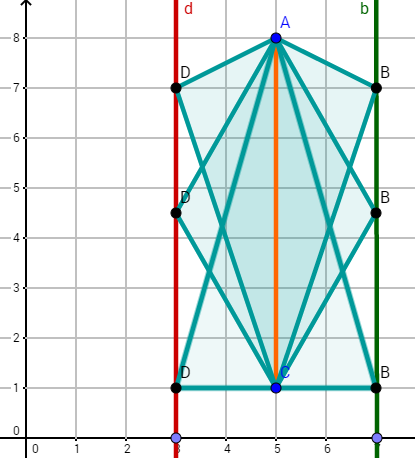
Zeichne zuerst die Punkte , und die Gerade in ein Koordinatensystem.
Die Punkte und liegen auf der Geraden . Ergänze die Dreiecke und jeweils zu einem Drachenviereck bzw. .
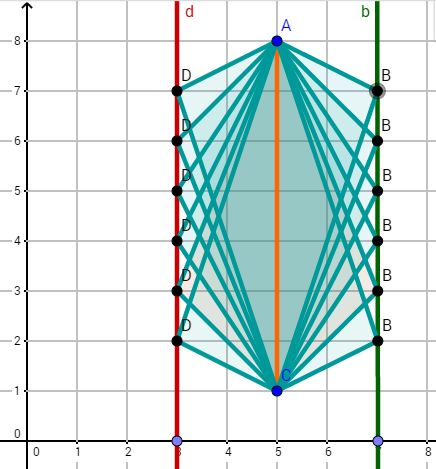
Für jeden Punkt auf der Geraden kann man das Dreieck zu einem Drachenviereck ergänzen. Alle Punkte liegen auf einer Geraden. Zeichne diese ein.
Nenne zwei Beispiele für die Punkte und , die auf den jeweiligen Geraden und liegen, dass das Drachenviereck entsteht.
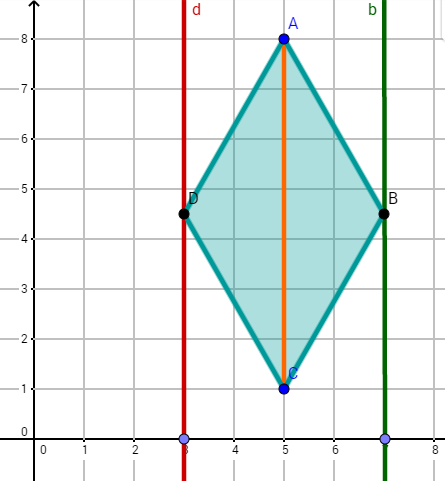
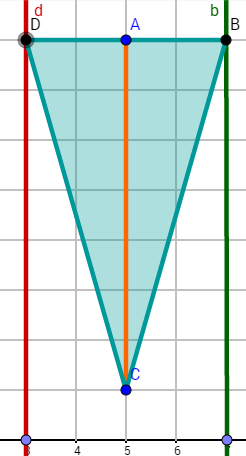
Wann ist das Drachenviereck eine Raute? Versuche und jetzt so zu verschieben, dass sie mit oder mit ein Dreieck bilden?
Was fällt dir im Bezug auf die verschiedenen Drachendreiecke/Raute/Dreiecke am Flächeninhalt auf?
- 2
Welche der folgenden Vierecke sind Rauten?
- 3
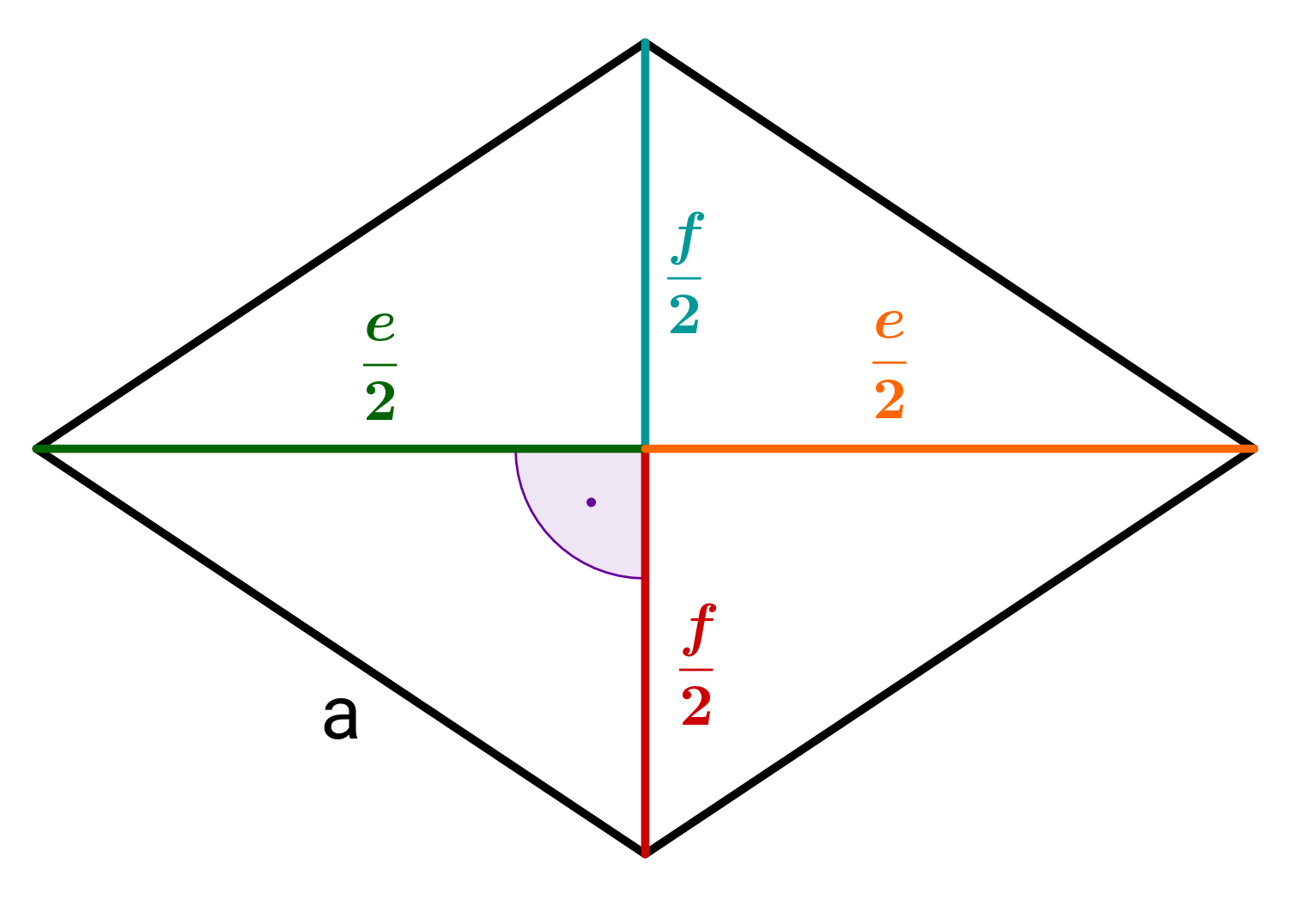
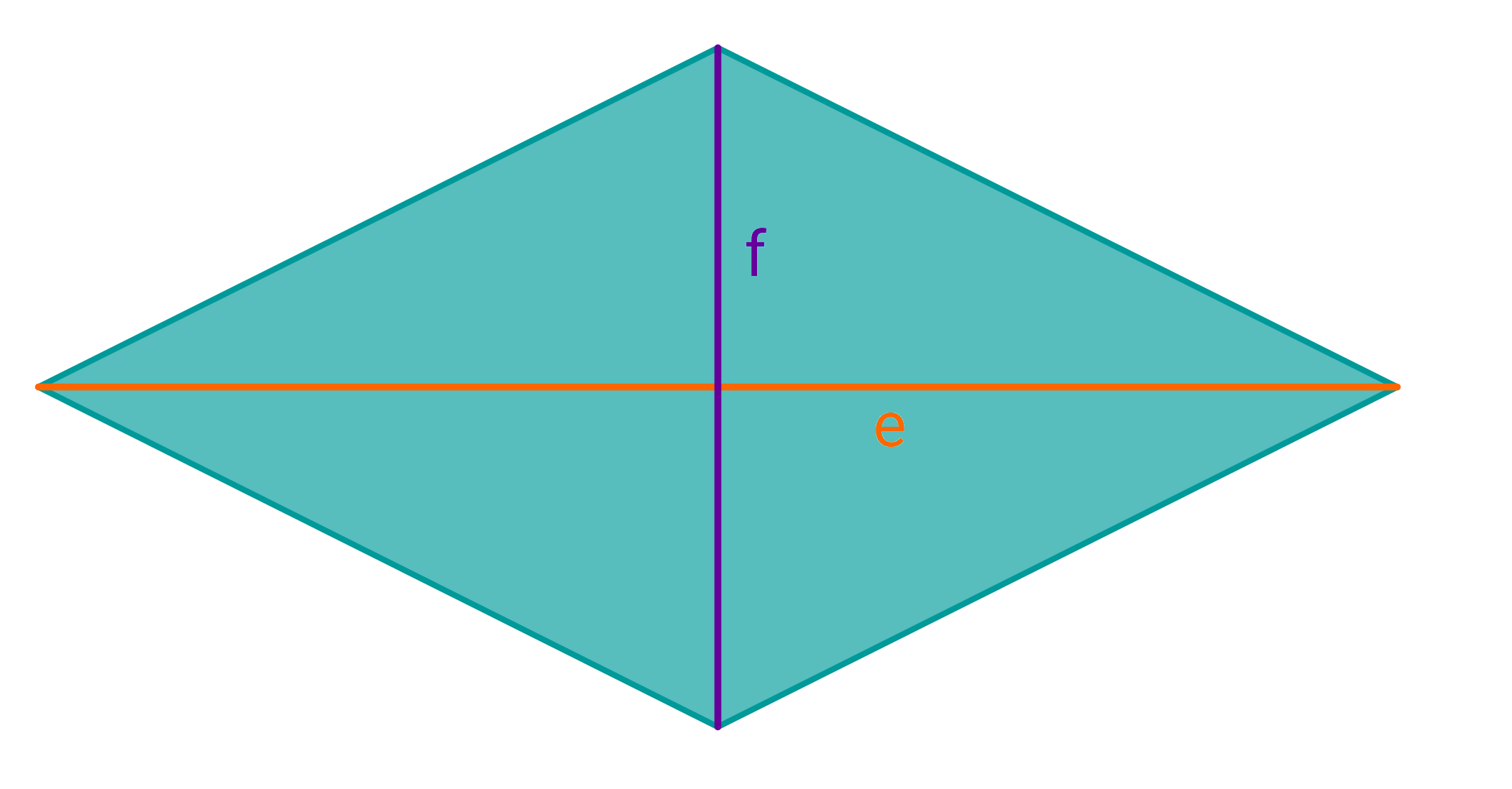
Wie berechnet man den Flächeninhalt von einem Drachenviereck?
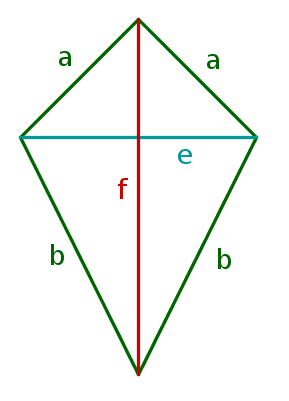
- 4
Berechne den Umfang der Raute im Bild auf eine Nachkommastelle genau, wobei und lang sind.
 cm
cm - 5
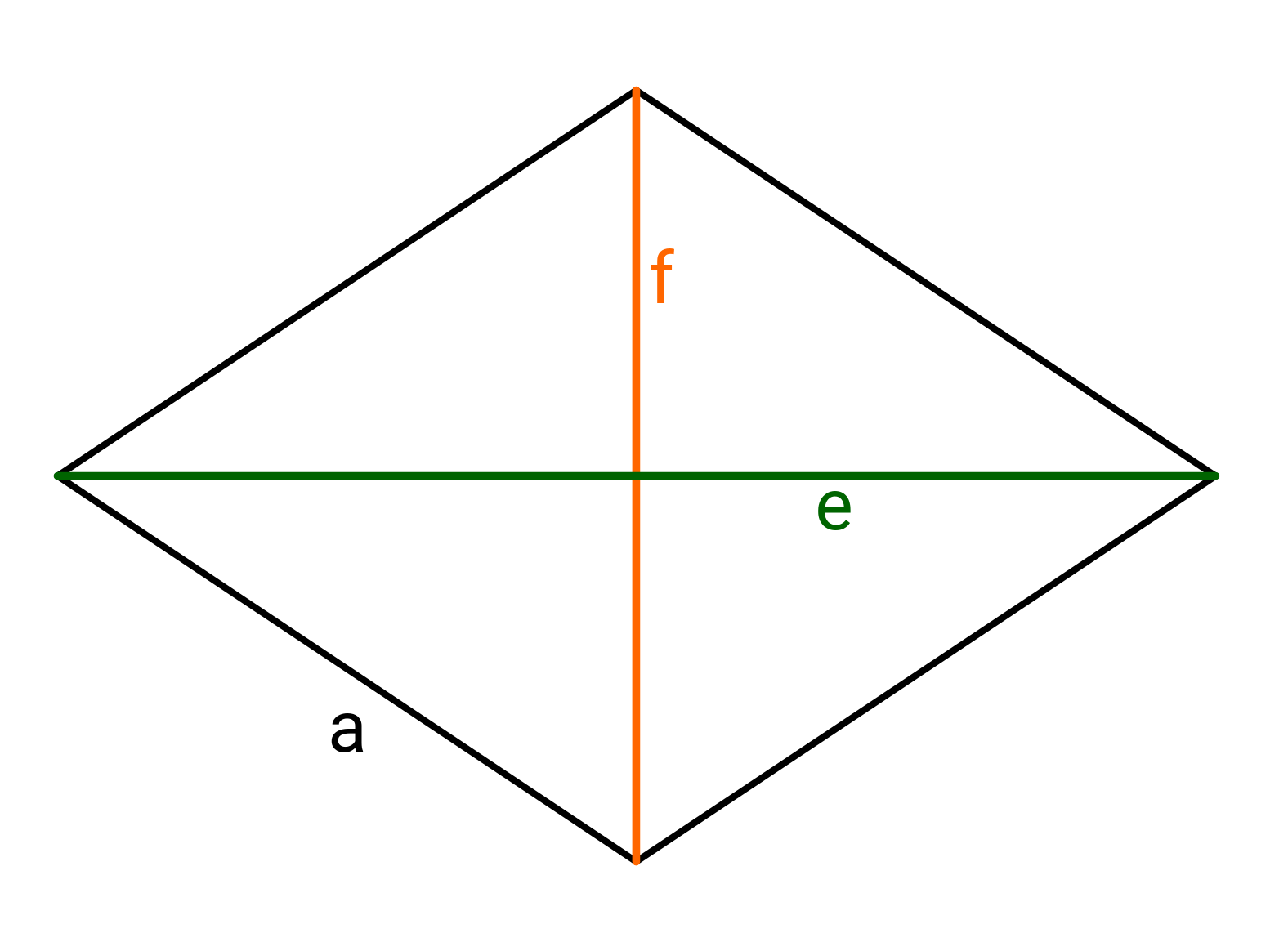
Von einer Raute kennst du die Fläche und die Länge der Diagonalen . Wie lang ist die Diagonale ?
 cm
cm - 6
Berechne die fehlende Größe des Drachenvierecks.

- cm²
- cm²
- dm²
- cm²
- cm
- cm
- cm
- dm