Aufgaben zu Äquivalenzrelationen
- 1
Betrachte die Relation " und besitzen dieselbe ISB-Nummer" auf der Grundmenge aller bisher gedruckten Buchexemplare.
Welche Eigenschaften besitzt diese Relation?
- 2
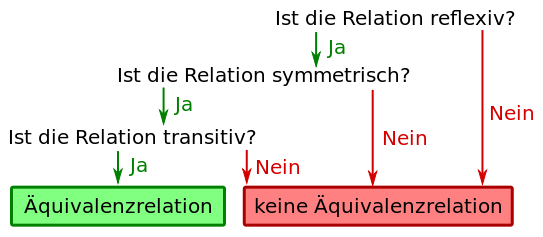
Was muss man machen, wenn man entscheiden will, ob eine Relation eine Äquivalenzrelation ist oder nicht?
- 3
Entscheide, welche der folgenden Relationen eine Äquivalenzrelation ist:
„ und gehen in dieselbe Klasse“ auf der Menge aller Schüler einer Schule
„“ auf der Menge der ganzen Zahlen
„ und sind ungerade“ auf der Menge
„ und besitzen denselben Rest bei der Division durch zwei“ auf der Menge
�„“ auf einer beliebigen, nicht-leeren Grundmenge
- 4
Wie viele lineare Äquivalenzrelationen auf einer Grundmenge gibt es?
- 5
Beschreibe, wie die Äquivalenzklassen der folgenden Äquivalenzrelationen aussehen:
„ und gehen in dieselbe Klasse“ auf der Menge aller Schüler einer Schule
„ und besitzen denselben Rest bei der Division durch zwei“ auf der Menge
„“ auf einer beliebigen, nicht leeren Grundmenge
- 6
Beweise die folgenden Sätze:
Sei eine Äquivalenzrelation auf der Grundmenge . Dann ist die Menge aller Äquivalenzklassen eine Zerlegung der Grundmenge.
Sei eine Menge und eine Zerlegung dieser Menge. Dann gibt es genau eine Äquivalenzrelation , die diese Zerlegung induziert, für die also ist. Diese Äquivalenzrelation ist definiert durch:
- 7
Sei eine Menge und eine Zerlegung dieser Menge. Es sei die Relation durch die folgende Eigenschaft definiert:
Beweise die folgenden Aussagen:
ist eine Äquivalenzrelation