Nachtermin Teil B

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Aufgabe B 1

Rauten $A B_{n} C D_{n}$ besitzen die gemeinsame Diagonale $A C$ . Die Winkel $∢ C B_{n} A$ haben das Maß $φ$ mit $φ \in] 0^{\circ}; 180^{\circ} [$ .

Es gilt: $A C = 5 cm$ .

Die Zeichnung zeigt die Raute $A B_{1} C D_{1}$ mit den Diagonalen $A C$ und $B_{1} D_{1}$ für $φ = 110^{\circ}$ .

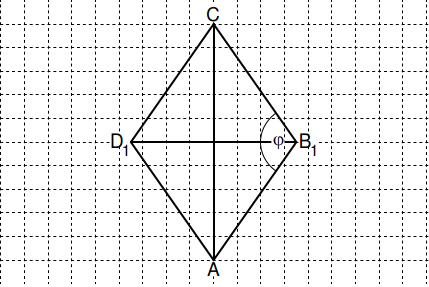
Zeichnen Sie die Raute $A B_{2} C D_{2}$ für $φ = 80^{\circ}$ in die Zeichnung zur Aufgabenstellung ein. (1 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Raute
Die beiden Symmetrieachsen der Raute sollen die Koordinatenachsen sein. Dann liegt die Mitte der Raute im Koordinatenursprung.
Berechnung der Länge der halben Diagonalen $D_{2} B_{2}$ ,
Für die Zeichnung werden z.B. die Koordinaten des Punktes $B_{2}$ benötigt.
Skizze des rechten oberen Dreiecks:
Dann gilt:
$\tan 40^{\circ} = \frac{2,5}{x_{B_{2}}} \Rightarrow x_{B_{2}} = \frac{2,5}{\tan 40^{\circ}} \approx 3 \Rightarrow B_{2} (3 | 0)$
Damit kann dann die Raute $A B_{2} C D_{2}$ für $φ = 80^{\circ}$ gezeichnet werden.
Eingezeichnete Raute $A B_{2} C D_{2}$
Für die Zeichnung braucht man die Länge der halben Diagonalen $D_{2} B_{2}$ , die im rechten oberen Dreieck mit dem Tangens berechnet werden kann.
Mit dieser Länge kann dann die Raute $A B_{2} C D_{2}$ gezeichnet werden.
Zeigen Sie, dass für den Umfang $u$ der Rauten $A B_{n} C D_{n}$ in Abhängigkeit von $φ$ gilt:
$u (φ) = \frac{10}{\sin (0,5 φ)} cm$ . (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Raute
Zeige, dass für den Umfang $u$ der Rauten $A B_{n} C D_{n}$ in Abhängigkeit von $φ$ gilt: $u (φ) = \frac{10}{\sin (0,5 φ)} cm$
Der Umfang der Raute ist:
$u = 4 \cdot | A B_{n} |$
Berechnung von $| A B_{n} |$ mithilfe des Sinus
Im unteren rechtwinkligen Dreieck $O A B_{2}$ gilt:
$\sin (0,5 φ) = \frac{0,5 \cdot | A C |}{| A B_{n} |} = \frac{2,5 cm}{| A B_{n} |}$
$\Rightarrow | A B_{n} | (φ) = \frac{2,5}{\sin (0,5 φ)} cm$ für $φ \in] 0^{\circ}; 180^{\circ} [$
Damit erhält man für $u$ :
$u = 4 \cdot | A B_{n} | = 4 \cdot \frac{2,5}{\sin (0,5 φ)} = \frac{10}{\sin (0,5 φ)} cm$
Damit ist gezeigt, dass für den Umfang $u$ der Rauten $A B_{n} C D_{n}$ in Abhängigkeit von $φ$ gilt: $u (φ) = \frac{10}{\sin (0,5 φ)} cm$ .
Der Umfang der Raute ist $u = 4 \cdot | A B_{n} |$ .
Berechne im unteren rechtwinkligen Dreieck $| A B_{n} |$ mithilfe des Sinus.

Der Umfang der Raute $A B_{3} C D_{3}$ ist um $15 %$ kleiner als der Umfang der Raute $A B_{1} C D_{1}$ .

Berechnen Sie das zugehörige Maß $φ$ des Winkels $C B_{3} A$ .

Runden Sie auf zwei Stellen nach dem Komma. (3 P)

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe B 2
Kongruente, gleichschenklige Dreiecke $A_{n} B_{n} C$ und $C D_{n} E_{n}$ besitzen den gemeinsamen Punkt $C$ . Diese Dreiecke haben die Basen $A_{n} B_{n}$ und $D_{n} E_{n}$ mit den Mittelpunkten $S_{n}$ und $T_{n}$ .
Es gilt: $| A_{n} B_{n} | = | D_{n} E_{n} | = 6 cm$ .
Die Winkel $E_{n} C A_{n}$ und $B_{n} C D_{n}$ haben jeweils das Maß $φ$ mit $φ \in] 0^{\circ}; 180^{\circ} [$ .
Die nebenstehende Skizze zeigt die Dreiecke $A_{1} B_{1} C$ und $C D_{1} E_{1}$ für $φ = 100^{\circ}$ .
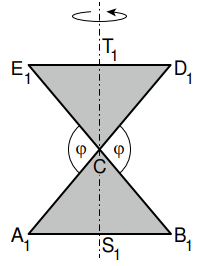
Die Dreiecke $A_{n} B_{n} C$ und $C D_{n} E_{n}$ rotieren um die Gerade $S_{n} T_{n}$ . In der Skizze ist der Axialschnitt des für $φ = 100^{\circ}$ entstehenden Rotationskörpers grau eingefärbt.
Berechnen Sie die Länge der Strecken $C T_{n}$ sowie das Volumen der entstehenden Rotationskörper in Abhängigkeit von $φ$ .
$[$ Ergebnisse: $| C T_{n} | (φ) = 3 \cdot \tan (\frac{φ}{2}) cm$ ; $V (φ) = 18 \cdot π \cdot \tan (\frac{φ}{2}) {cm}^{3}]$ (2,5 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens
Berechne die Länge der Strecken $C T_{n}$ in Abhängigkeit von $φ$
Die Abbildung ist nicht in der Aufgabenstellung gefordert. Sie dient nur zur Veranschaulichung.
Im oberen Dreieck gilt:
$\tan (\frac{φ}{2}) = \frac{| C T_{n} |}{| E_{n} T_{n} |}$
Dabei ist $| E_{n} T_{n} | = 0,5 \cdot | D_{n} E_{n} | = 0,5 \cdot 6 = 3 cm$ .
$\Rightarrow | C T_{n} | (φ) = | E_{n} T_{n} | \cdot \tan (\frac{φ}{2}) = 3 \cdot \tan (\frac{φ}{2}) cm$
Die Länge der Strecken $C T_{n}$ in Abhängigkeit von $φ$ lautet:
$| C T_{n} | (φ) = 3 \cdot \tan (\frac{φ}{2}) cm$
Berechne das Volumen des zugehörigen Rotationskörpers
$V = 2 \cdot V_{Kegel}$
$V_{Kegel} = \frac{1}{3} \cdot G \cdot h$
Die Grundfläche ist ein Kreis $G = π \cdot r^{2}$ mit $r = 3 cm$ und $h = | C T_{n} | (φ)$ .
Dann folgt für das gesuchte Volumen:
$V (φ) = 2 \cdot \frac{1}{3} \cdot π \cdot 3^{2} \cdot 3 \cdot \tan (\frac{φ}{2}) = 18 \cdot π \cdot \tan (\frac{φ}{2}) {cm}^{3}$
Das Volumen des zugehörigen Rotationskörpers ist $V (φ) = 18 \cdot π \cdot \tan (\frac{φ}{2}) {cm}^{3}$
Teil 1
Berechne $\tan (\frac{φ}{2})$ und löse nach $| C T_{n} |$ auf.
Teil 2
Es ist $V = 2 \cdot V_{Kegel}$ mit $V_{Kegel} = \frac{1}{3} \cdot G \cdot h$ .
Die Grundfläche ist ein Kreis und die Höhe $h$ ist $h = | C T_{n} | (φ)$ .

Die Dreiecke $A_{2} B_{2} C$ und $C D_{2} E_{2}$ sind gleichseitig.
Berechnen Sie das Volumen des zugehörigen Rotationskörpers.
Runden Sie auf zwei Stellen nach dem Komma. (1,5 P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegel
Bekannt ist, dass die Dreiecke $A_{2} B_{2} C$ und $C D_{2} E_{2}$ gleichseitig sind.
Für den Winkel gilt dann:
$\frac{φ}{2} = 60^{\circ} \Rightarrow φ = 120^{\circ}$
$\Rightarrow V (120^{\circ}) = 18 \cdot π \cdot \tan (\frac{120^{\circ}}{2}) \approx 97,95$
Das Volumen des zugehörigen Rotationskörpers beträgt rund $97,95 {cm}^{3}$ .
Beachte, dass im gleichseitigen Dreieck alle Winkel gleich $60^{\circ}$ sind.
Berechne $V (120^{\circ})$ .

Aufgabe B 3

Gegeben sind die Funktionen $f_{1}$ mit der Gleichung $y = - 1,5 \cdot \log_{0,5} (x + 3) + 1$ und $f_{2}$ mit der Gleichung $y = 1,5 \cdot \log_{0,5} (x + 2) + 1 (x, y \in ℝ)$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Berechnen Sie die Nullstelle der Funktion $f_{1}$ und zeichnen Sie den Graphen zu $f_{1}$ für $x \in [- 2,5; 10]$ sowie den Graphen zu $f_{2}$ für $x \in [- 1,5; 10]$ in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit $1 cm$ ; $- 3 \leq x \leq 10; - 5 \leq y \leq 7$ (5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
Berechne die Nullstelle der Funktion $f_{1}$
Gegeben ist $y = - 1,5 \cdot \log_{0,5} (x + 3) + 1$ .
Für die Berechnung der Nullstelle setze $y = 0$ :
$0$ $=$ $- 1,5 \cdot \log_{0,5} (x + 3) + 1$ $+ 1,5 \cdot \log_{0,5} (x + 3)$
↓
Löse nach $x$ auf.
$1,5 \cdot \log_{0,5} (x + 3)$ $=$ $1$ $: 1,5$
$\log_{0,5} (x + 3)$ $=$ $\frac{2}{3}$ ${0,5}^{()}$
$x + 3$ $=$ ${0,5}^{\frac{2}{3}}$ $- 3$
$x$ $=$ ${0,5}^{\frac{2}{3}} - 3$
$x$ $\approx$ $- 2,37$
$L = {- 2,37}$
Die Nullstelle der Funktion $f_{1}$ liegt etwa bei $x = - 2,37$ .
Zeichne den Graphen zu $f_{1}$ für $x \in [- 2,5; 10]$ sowie den Graphen zu $f_{2}$ für $x \in [- 1,5; 10]$ in ein Koordinatensystem
Erstelle eine Wertetabelle für die beiden Funktionen in den angegebenen Intervallen. Trage die berechneten Punkte in ein Koordinatensystem ein und zeichne die beiden Funktionen.
$f_{1}$ für $x \in [- 2,5; 10]$
$x$
-2,5
-2,37
-1,5
-0,5
0
1
2
4
6
8
10
$y$
$- 0,52$
$0$
$1,87$
$2,98$
$3,38$
$4$
$4,48$
$5,21$
$5,75$
$6,19$
$6,55$
$f_{2}$ für $x \in [- 1,5; 10]$
$x$
-1,5
-0,5
0
1
2
4
6
8
10
$y$
$2,49$
$0,13$
$- 0,5$
$- 1,38$
$- 2$
$- 2,88$
$- 3,5$
$- 3,98$
$- 4,38$
$f_{1}$ und $f_{2}$
Teil 1
Setze $y = 0$ und löse nach $x$ auf.
Teil 2
Erstelle eine Wertetabelle für die beiden Funktionen in den angegebenen Intervallen. Trage die berechneten Punkte in ein Koordinatensystem ein und zeichne die beiden Funktionen.
Punkte $A_{n} (x | - 1,5 \cdot \log_{0,5} (x + 3) + 1)$ auf dem Graphen zu $f_{1}$ haben dieselbe Abszisse $x$ wie Punkte auf dem Graphen zu $f_{2}$ . Zusammen mit den Punkten $C (9 | - 3)$ und $D (9 | 4)$ sind sie für $- 1,38 < x < 9$ Eckpunkte von Trapezen $A_{n} B_{n} C D$ .
Zeichnen Sie das Trapez $A_{1} B_{1} C D$ für $x = - 0,5$ und das Trapez $A_{2} B_{2} C D$ für $x = 6$ in das Koordinatensystem zur Aufgabe b) ein. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Trapez
Zeichne das Trapez $A_{1} B_{1} C D$ für $x = - 0,5$ und das Trapez $A_{2} B_{2} C D$ für $x = 6$ in das Koordinatensystem zur Aufgabe b) ein
Für das Trapez $A_{1} B_{1} C D$ :
Gegeben sind $C (9 | - 3)$ und $D (9 | 4)$ , sowie $A_{1} (- 0,5 | f_{1} (- 0,5))$ und $A_{2} (6 | f_{1} (6))$ .
Für das Trapez $A_{2} B_{2} C D$ :
Gegeben sind $C (9 | - 3)$ und $D (9 | 4)$ , sowie $B_{2} (- 0,5 | f_{2} (- 0,5))$ und $A_{2} (6 | f_{2} (6))$ .
Trage alle Punkte ein und verbinde sie.
Eingezeichnete Trapeze $A_{1} B_{1} C D$ und $A_{2} B_{2} C D$
Für das Trapez $A_{1} B_{1} C D$ :
Gegeben sind $C (9 | - 3)$ und $D (9 | 4)$ , sowie $A_{1} (- 0,5 | f_{1} (- 0,5))$ und $A_{2} (6 | f_{1} (6)) .$
Für das Trapez $A_{2} B_{2} C D$ :
Gegeben sind $C (9 | - 3)$ und $D (9 | 4)$ , sowie $B_{2} (- 0,5 | f_{2} (- 0,5))$ und $A_{2} (6 | f_{2} (6))$ .
Trage alle Punkte ein und verbinde sie.
Berechnen Sie das Maß des Winkels $B_{2} A_{2} D$ . (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangensfunktion
Berechne das Maß des Winkels $B_{2} A_{2} D$
Geben ist $D (9 | 4)$ .
Berechne $\tan ∢ B_{2} A_{2} D$ :
$\tan ∢ B_{2} A_{2} D = \frac{x_{D} - x_{A_{2}}}{y_{A_{2}} - y_{D}}$ , dabei ist $A_{2} (6 | - 1,5 \cdot \log_{0,5} (6 + 3) + 1)) \Rightarrow A_{2} (6 | 5,75)$
Dann folgt für den gesuchten Winkel:
$\tan ∢ B_{2} A_{2} D = \frac{x_{D} - x_{A_{2}}}{y_{A_{2}} - y_{D}} = \frac{9 - 6}{5,75 - 4} = \frac{3}{1,75}$
$\Rightarrow ∢ B_{2} A_{2} D = \tan^{- 1} (\frac{3}{1,75}) \approx {59,74}^{\circ}$
Das Maß des Winkels $B_{2} A_{2} D$ beträgt rund ${59,74}^{\circ}$ .
Berechne $\tan ∢ B_{2} A_{2} D$ .

$x$	-2,5	-2,37	-1,5	-0,5	0	1	2	4	6	8	10
$y$	$- 0,52$	$0$	$1,87$	$2,98$	$3,38$	$4$	$4,48$	$5,21$	$5,75$	$6,19$	$6,55$

$x$	-1,5	-0,5	0	1	2	4	6	8	10
$y$	$2,49$	$0,13$	$- 0,5$	$- 1,38$	$- 2$	$- 2,88$	$- 3,5$	$- 3,98$	$- 4,38$

Die Länge der Strecken $A_{n} B_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $A_{n}$ lässt sich durch einen Term der Form $| A_{n} B_{n} | (x) = [- 1,5 \cdot \log_{0,5} (x^{2} + b x + c)] LE$ mit $b, c \in ℝ$ darstellen.

Bestimmen Sie rechnerisch die Werte für $b$ und $c$ . (2,5 P)

Begründen Sie rechnerisch, weshalb es unter den Trapezen $A_{n} B_{n} C D$ kein Rechteck $A_{3} B_{3} C D$ gibt. (3,5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
Begründe rechnerisch, weshalb es unter den Trapezen $A_{n} B_{n} C D$ kein Rechteck $A_{3} B_{3} C D$ gibt
Wenn es ein Rechteck $A_{3} B_{3} C D$ gäbe, dann müsste gelten:
$y_{A_{3}} = y_{D} = 4$ und $y_{B_{3}} = y_{C} = - 3$ .
Löse die Gleichung $y_{A_{3}} = 4$ nach $x$ auf.
$4$ $=$ $- 1,5 \cdot \log_{0,5} (x + 3) + 1$ $- 1$
↓
Löse nach $x$ auf.
$3$ $=$ $- 1,5 \cdot \log_{0,5} (x + 3)$ $: (- 1,5)$
$- 2$ $=$ $\log_{0,5} (x + 3)$ ${0,5}^{()}$
${0,5}^{- 2}$ $=$ $x + 3$ $- 3$
${0,5}^{- 2} - 3$ $=$ $x$
$4 - 3$ $=$ $x$
$1$ $=$ $x$
$L = {1}$
Berechne nun $y_{B_{3}} (1)$ :
$y_{B_{3}} = 1,5 \cdot \log_{0,5} (1 + 2) + 1 = 1,5 \cdot \log_{0,5} (3) + 1 \approx - 1,38$ .
Das Ergebnis $y_{B_{3}} = - 1,38$ widerspricht aber der geforderten Gleichung $y_{B_{3}} = y_{C} = - 3$ .
Daher gibt es kein Rechteck $A_{3} B_{3} C D$ .
Wenn es ein Rechteck $A_{3} B_{3} C D$ gäbe, dann müsste gelten: $y_{A_{3}} = y_{D} = 4$ und $y_{B_{3}} = y_{C} = - 3$ .
Löse die Gleichung $y_{A_{3}} = 4$ nach $x$ auf. $\Rightarrow x_{1}$
Berechne $y_{B_{3}} (x_{1})$ und vergleiche das Ergebnis mit der Gleichung $y_{B_{3}} = y_{C} = - 3$ .

Aufgabe B 4

Die Diagonalen $A C$ und $B D$ des Drachenvierecks $A B C D$ schneiden sich im Punkt $M$ .

Das Drachenviereck $A B C D$ ist die Grundfläche der Pyramide $A B C D S$ mit der Höhe $M S$ .

Es gilt: $| A C | = 12 cm; | C M | = 8 cm; | B D | = 8 cm; | M S | = 7 cm$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Zeichnen Sie das Schrägbild der Pyramide $A B C D S$ , wobei die Strecke $A C$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $C$ liegen soll.
Für die Zeichnung gilt: $q = \frac{1}{2}; ω = 45^{\circ}$ .
Berechnen Sie sodann die Länge der Strecke $S C$ und das Maß des Winkels $M S C$ .
$[$ Teilergebnisse: $| S C | = 10,63 cm; ∢ M S C = {48,81}^{\circ}]$ (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder zeichnen
Zeichne das Schrägbild der Pyramide $A B C D S$ , wobei die Strecke $A C$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $C$ liegen soll
Zeichne die Pyramide, beachte für die Strecke $B D$ : $q = \frac{1}{2}$ und $ω = 45^{\circ}$ .
Pyramide $A B C D S$
Berechne die Länge der Strecke $S C$
Betrachte das rechtwinklige Dreieck $S C M$ . Benutze den Satz des Pythagoras.
Hier gilt:
$| C M |^{2} + | M S |^{2} = | S C |^{2} \Rightarrow \sqrt{8^{2} + 7^{2}} = | S C |$
$| S C | \approx 10,63 cm$
Die Länge der Strecke $S C$ beträgt rund $10,63 cm$ .
Berechne das Maß des Winkels $M S C$
Betrachte das rechtwinklige Dreieck $S C M$ . Benutze den Tangens:
$\tan ∢ M S C = \frac{| C M |}{| M S |} = \frac{8}{7} \Rightarrow ∢ M S C = \tan^{- 1} (\frac{8}{7}) \approx {48,81}^{\circ}$
Das Maß des Winkels $M S C$ beträgt rund ${48,81}^{\circ}$ .
Teil 1
Zeichne die Pyramide, beachte für die Strecke $B D$ : $q = \frac{1}{2}$ und $ω = 45^{\circ}$ .
Teil 2
Betrachte das rechtwinklige Dreieck $S C M$ .
Streckenlänge: Benutze den Satz des Pythagoras.
Teil 3
Betrachte das rechtwinklige Dreieck $S C M$ .
Winkelberechnung: Benutze den Tangens.
Punkte $E_{n}$ liegen auf der Strecke $M C$ . Die Winkel $M S E_{n}$ haben das Maß $φ$ mit $φ \in [0^{\circ}; {48,81}^{\circ}]$ . Für Punkte $P_{n} \in S E_{n}$ gilt: $| S P_{n} | = 6 cm$ .
Zeichnen Sie die Strecke $S E_{1}$ sowie den Punkt $P_{1}$ für $φ = 40^{\circ}$ in das Schrägbild zu Aufgabe a) ein. (1 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel konstruieren
Zeichne die Strecke $S E_{1}$ sowie den Punkt $P_{1}$ für $φ = 40^{\circ}$ in das Schrägbild zu Aufgabe a) ein
Trage im Punkt $S$ den Winkel $φ = 40^{\circ}$ an die Strecke $M S$ an.
Der freie Schenkel schneidet die Strecke $A C$ im Punkt $E_{1}$ .
Zeichne einen Kreis um $S$ mit dem Radius $r = 6 c m$ .
Du erhältst den Punkt $P_{1}$ auf der Strecke $S E_{1}$ .
Anmerkung: Der Kreis um $S$ ist in der Abbildung nicht dargestellt, nur sein Schnittpunkt $P_{1}$ mit der Strecke $S E_{1}$ .
Pyramide mit eingezeichneten Punkten $E_{1}$ , $P_{1}$ und $S E_{1}$
Trage im Punkt $S$ den Winkel $φ = 40^{\circ}$ an die Strecke $M S$ an.
Der freie Schenkel schneidet die Strecke $A C$ im Punkt $E_{1}$ .
Zeichne einen Kreis um $S$ mit dem Radius $r = 6; cm$ .
Du erhältst den Punkt $P_{1}$ auf der Strecke $S E_{1}$ .
Punkte $T_{n}$ sind die Fußpunkte der Lote von den Punkten $P_{n}$ auf die Strecke $M S$ .
Zeichnen Sie die Strecke $P_{1} T_{1}$ in das Schrägbild zu Aufgabe a) ein.
Zeigen Sie sodann, dass für die Länge der Strecken $M T_{n}$ in Abhängigkeit von $φ$ gilt:
$| M T_{n} | (φ) = (7 - 6 \cdot \cos φ) cm$ . (2,5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallele Geraden konstruieren
Zeichne die Strecke $P_{1} T_{1}$ in das Schrägbild zu Aufgabe a) ein
Zeichne eine zur Strecke $A C$ parallele Strecke, die im Punkt $P_{1}$ beginnt und im Punkt $T_{1}$ endet.
Pyramide mit Strecke $P_{1} T_{1}$
Zeige sodann, dass für die Länge der Strecken $M T_{n}$ in Abhängigkeit von $φ$ gilt: $| M T_{n} | (φ) = (7 - 6 \cdot \cos φ) cm$
Bekannt sind $| S P_{n} | = 6 cm$ und $| M S | = 7 cm$
Außerdem gilt:
$| M T_{n} | = | M S | - | S T_{n} |$
Für den $\cos φ$ im rechtwinkligen Dreieck $S P_{n} T_{n}$ gilt dann:
$\cos φ = \frac{| S T_{n} |}{| S P_{n} |} = \frac{| S T_{n} |}{6 cm} \Rightarrow | S T_{n} | (φ) = 6 \cdot \cos φ cm$ mit $φ \in [0^{\circ}; {48,81}^{\circ}]$
Dann erhält man:
$| M T_{n} | = | M S | - | S T_{n} | = (7 - 6 \cdot \cos φ) cm$
Ergebnis: $| M T_{n} | (φ) = (7 - 6 \cdot \cos φ) cm$ mit $φ \in [0^{\circ}; {48,81}^{\circ}]$
Teil 1
Zeichne eine zur Strecke $A C$ parallele Strecke, die im Punkt $P_{1}$ beginnt und im Punkt $T_{1}$ endet.
Teil 2
Bekannt sind $| S P_{n} | = 6 cm$ und $| M S | = 7 cm$ und es gilt: $| M T_{n} | = | M S | - | S T_{n} |$
Berechne den $\cos φ$ im rechtwinkligen Dreieck $S P_{n} T_{n}$ .
Unter den Strecken $M T_{n}$ hat die Strecke $M T_{0}$ die maximale Länge.
Geben Sie den zugehörigen Wert für $φ$ an. (1 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel
Gib den zugehörigen Wert für $φ$ an
Je kleiner der Winkel $φ$ wird, desto kleiner wird die Strecke $M T_{n}$ .
Anderseits wird die Strecke $M T_{n}$ maximal, wenn $φ$ maximal wird.
Der maximale Wert, den $φ$ annehmen kann, ist $φ = ∢ M S C = {48,81}^{\circ}$
(siehe Aufgabe a).
Für $φ = {48,81}^{\circ}$ hat die Strecke $M T_{0}$ die maximale Länge.
Die Strecke $M T_{n}$ wird maximal, wenn $φ$ maximal wird.
Siehe Aufgabe a).
Die Punkte $P_{n}$ sind die Spitzen von Pyramiden $B C D P_{n}$ mit den Höhen $P_{n} F_{n}$ $(F_{n} \in M C)$ .
Zeichnen Sie die Pyramide $B C D P_{1}$ und die Höhe $P_{1} F_{1}$ in das Schrägbild zu Aufgabe a) ein.
Zeigen Sie durch Rechnung, dass für das Volumen $V$ der Pyramiden $B C D P_{n}$ in Abhängigkeit von $φ$ gilt: $V (φ) = (74,67 - 64 \cdot \cos φ) {cm}^{3}$ . (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Zeichne die Pyramide $B C D P_{1}$ und die Höhe $P_{1} F_{1}$ in das Schrägbild zu Aufgabe a) ein
Zeichne die Pyramide $B C D P_{1}$ und die Höhe $P_{1} F_{1}$ ein.
Pyramide $B C D P_{1}$ und die Höhe $P_{1} F_{1}$ (grün)
Zeige durch Rechnung, dass für das Volumen $V$ der Pyramiden $B C D P_{n}$ in Abhängigkeit von $φ$ gilt: $V (φ) = (74,67 - 64 \cdot \cos φ) {cm}^{3}$
$V = \frac{1}{3} \cdot G \cdot h$ .
Dabei ist die Grundfläche $G$ ein Dreieck mit der Grundseite $| B D | = 8 cm$ und der Höhe $| C M | = 8 cm$ .
$A_{Dreieck} = \frac{1}{2} \cdot | B D | \cdot | C M | = \frac{1}{2} \cdot 8 \cdot 8 = 32 {cm}^{2}$
Die Pyramidenhöhe ist $| P_{n} F_{n} | = | M T_{n} | (φ) = (7 - 6 \cdot \cos φ) cm$ .
Dann folgt für das Pyramidenvolumen:
$V (φ) = \frac{1}{3} \cdot 32 \cdot (7 - 6 \cdot \cos φ) = (74,67 - 64 \cdot \cos φ) {cm}^{3}$
Das Volumen $V$ der Pyramiden $B C D P_{n}$ in Abhängigkeit von $φ$ ist:
$V (φ) = (74,67 - 64 \cdot \cos φ) {cm}^{3}$
Teil 1
Zeichne die Pyramide $B C D P_{1}$ und die Höhe $P_{1} F_{1}$ ein.
Teil 2
$V_{P} = \frac{1}{3} \cdot G \cdot h$
Die Grundfläche $G$ ist ein Dreieck mit der Grundseite $| B D | = 8 cm$ und der Höhe $| C M | = 8 cm$ .
Die Pyramidenhöhe ist $| P_{n} F_{n} | = | M T_{n} | (φ) = (7 - 6 \cdot \cos φ) cm$ .
Das Volumen der Pyramide $B C D P_{2}$ beträgt $\frac{1}{5}$ des Volumens der Pyramide $A B C D S$ .
Berechnen Sie den zugehörigen Wert für $φ$ . (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Berechne den zugehörigen Wert für $φ$
Das Pyramidenvolumen der Pyramide $A B C D S$ ist:
$V_{A B C D S} = \frac{1}{3} \cdot G \cdot h$
Dabei ist die Grundseite ein Drachenviereck mit den beiden Diagonalen $| A C | = 12 cm$ und $| B C | = 8 cm$ .
$\Rightarrow G = A_{Drache} = \frac{1}{2} \cdot | A C | \cdot | B C | = \frac{1}{2} \cdot 12 \cdot 8 = 48 {cm}^{2}$
Die Pyramidenhöhe ist $| M S | = 7 cm$ .
Dann folgt für das Pyramidenvolumen:
$V_{ABCDS} = \frac{1}{3} \cdot 48 \cdot 7 = 112 {cm}^{3}$
Das Volumen der Pyramide $B C D P_{2}$ beträgt $\frac{1}{5}$ des Volumens der Pyramide $A B C D S$ .
Demnach hat die Pyramide $B C D P_{2}$ ein Volumen von:
$V_{B C D P_{2}} = \frac{112}{5} = 22,4 {cm}^{3}$ .
Also gilt:
$V (φ) = (74,67 - 64 \cdot \cos φ) {cm}^{3} = 22,4 {cm}^{3}$ für $φ \in [0^{\circ}; {48,81}^{\circ}]$ .
Jetzt können wir das nach $φ$ umformen:
$74,67 - 64 \cdot \cos φ$ $=$ $22,4$ $+ 64 \cdot \cos φ$
$74,67$ $=$ $64 \cdot \cos φ + 22,4$ $- 22,4$
$52,27$ $=$ $64 \cdot \cos φ$ $: 64$
$\frac{52,27}{64}$ $=$ $\cos φ$
$\cos φ = \frac{52,27}{64} \Rightarrow φ = \cos^{- 1} (\frac{52,27}{64}) \approx {35,24}^{\circ}$
$L = {{35,24}^{\circ}}$
Der zugehörige Wert für $φ$ beträgt rund ${35,24}^{\circ}$ .
Berechne $\frac{1}{5}$ vom Pyramidenvolumen der Pyramide $A B C D S$ . Nenne dieses zum Beispiel $V_{1}$ .
Setze $V_{1}$ gleich $V (φ)$ und löse nach $φ$ auf.

Das Dreieck $S P_{3} C$ ist gleichschenklig.

Bestimmen Sie rechnerisch den zugehörigen Wert für $φ$ . (2,5 P)

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$0,85 \cdot 12,21$	$=$	$\frac{10}{\sin (0,5 φ)}$	$\cdot \sin (0,5 φ)$
	↓	Löse nach $φ$ auf.
$0,85 \cdot 12,21 \cdot \sin (0,5 φ)$	$=$	$10$	$: (0,85 \cdot 12,21)$
$\sin (0,5 φ)$	$=$	$\frac{10}{0,85 \cdot 12,21}$	$\sin^{- 1} ()$
$0,5 φ$	$=$	$\sin^{- 1} (\frac{10}{0,85 \cdot 12,21})$
$0,5 φ$	$\approx$	${74,48}^{\circ}$	$\cdot 2$
$φ$	$\approx$	${148,96}^{\circ}$

$\| A_{n} B_{n} \| (x)$	$=$	$[- 1,5 \cdot \log_{0,5} (x + 3) + 1 - (1,5 \cdot \log_{0,5} (x + 2) + 1)]$
	↓	Löse die Klammer auf.
	$=$	$[- 1,5 \cdot \log_{0,5} (x + 3) + 1 - 1,5 \cdot \log_{0,5} (x + 2) - 1]$
	↓	Fasse zusammen.
	$=$	$[- 1,5 \cdot \log_{0,5} (x + 3) - 1,5 \cdot \log_{0,5} (x + 2)]$
	↓	Klammere aus.
	$=$	$- 1,5 \cdot [\log_{0,5} (x + 3) + \log_{0,5} (x + 2)]$
	↓	Wende ein Logarithmusgesetz an.
	$=$	$- 1,5 \cdot [\log_{0,5} ((x + 3) \cdot (x + 2))]$
	↓	Rechne das Produkt aus.
	$=$	$- 1,5 \cdot [\log_{0,5} (x^{2} + 2 x + 3 x + 6)]$
	↓	Fasse zusammen.
	$=$	$- 1,5 \cdot [\log_{0,5} (x^{2} + 5 x + 6)]$

$\cos ({48,81}^{\circ} - φ)$	$=$	$\frac{{10,63}^{2} + 6^{2} - 6^{2}}{2 \cdot 10,63 \cdot 6}$
	↓	Vereinfache.
$\cos ({48,81}^{\circ} - φ)$	$=$	$\frac{10,63}{12}$	$\cos^{- 1} ()$
	↓	Löse nach $φ$ auf.
${48,81}^{\circ} - φ$	$=$	$\cos^{- 1} (\frac{10,63}{12})$
${48,81}^{\circ} - φ$	$\approx$	${27,65}^{\circ}$	$+ φ - {27,65}^{\circ}$
${21,16}^{\circ}$	$\approx$	$φ$

Nachtermin Teil B

Aufgabe B 1

Berechnung der Länge der halben Diagonalen $D_{2} B_{2}$ ,

Zeige, dass für den Umfang $u$ der Rauten $A B_{n} C D_{n}$ in Abhängigkeit von $φ$ gilt: $u (φ) = \frac{10}{\sin (0,5 φ)} cm$

Berechnung von $| A B_{n} |$ mithilfe des Sinus

Berechne den Umfang der Raute $A B_{1} C D_{1}$ für $φ = 110^{\circ}$ .

Berechne das zugehörige Maß $φ$ des Winkels $C B_{3} A$

Aufgabe B 2

Berechne die Länge der Strecken $C T_{n}$ in Abhängigkeit von $φ$

Berechne das Volumen des zugehörigen Rotationskörpers

Aufgabe B 3

Berechne die Nullstelle der Funktion $f_{1}$

Zeichne den Graphen zu $f_{1}$ für $x \in [- 2,5; 10]$ sowie den Graphen zu $f_{2}$ für $x \in [- 1,5; 10]$ in ein Koordinatensystem

Zeichne das Trapez $A_{1} B_{1} C D$ für $x = - 0,5$ und das Trapez $A_{2} B_{2} C D$ für $x = 6$ in das Koordinatensystem zur Aufgabe b) ein

Berechne das Maß des Winkels $B_{2} A_{2} D$

Bestimme rechnerisch die Werte für $b$ und $c$

Begründe rechnerisch, weshalb es unter den Trapezen $A_{n} B_{n} C D$ kein Rechteck $A_{3} B_{3} C D$ gibt

Aufgabe B 4

Zeichne das Schrägbild der Pyramide $A B C D S$ , wobei die Strecke $A C$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $C$ liegen soll

Berechne die Länge der Strecke $S C$

Berechne das Maß des Winkels $M S C$

Zeichne die Strecke $S E_{1}$ sowie den Punkt $P_{1}$ für $φ = 40^{\circ}$ in das Schrägbild zu Aufgabe a) ein

Zeichne die Strecke $P_{1} T_{1}$ in das Schrägbild zu Aufgabe a) ein

Zeige sodann, dass für die Länge der Strecken $M T_{n}$ in Abhängigkeit von $φ$ gilt: $| M T_{n} | (φ) = (7 - 6 \cdot \cos φ) cm$

Gib den zugehörigen Wert für $φ$ an

Zeichne die Pyramide $B C D P_{1}$ und die Höhe $P_{1} F_{1}$ in das Schrägbild zu Aufgabe a) ein

Pyramide $B C D P_{1}$ und die Höhe $P_{1} F_{1}$ (grün)

Zeige durch Rechnung, dass für das Volumen $V$ der Pyramiden $B C D P_{n}$ in Abhängigkeit von $φ$ gilt: $V (φ) = (74,67 - 64 \cdot \cos φ) {cm}^{3}$

Berechne den zugehörigen Wert für $φ$

Bestimme rechnerisch den zugehörigen Wert für $φ$

$0$	$=$	$- 1,5 \cdot \log_{0,5} (x + 3) + 1$	$+ 1,5 \cdot \log_{0,5} (x + 3)$
	↓	Löse nach $x$ auf.
$1,5 \cdot \log_{0,5} (x + 3)$	$=$	$1$	$: 1,5$
$\log_{0,5} (x + 3)$	$=$	$\frac{2}{3}$	${0,5}^{()}$
$x + 3$	$=$	${0,5}^{\frac{2}{3}}$	$- 3$
$x$	$=$	${0,5}^{\frac{2}{3}} - 3$
$x$	$\approx$	$- 2,37$

$4$	$=$	$- 1,5 \cdot \log_{0,5} (x + 3) + 1$	$- 1$
	↓	Löse nach $x$ auf.
$3$	$=$	$- 1,5 \cdot \log_{0,5} (x + 3)$	$: (- 1,5)$
$- 2$	$=$	$\log_{0,5} (x + 3)$	${0,5}^{()}$
${0,5}^{- 2}$	$=$	$x + 3$	$- 3$
${0,5}^{- 2} - 3$	$=$	$x$
$4 - 3$	$=$	$x$
$1$	$=$	$x$

$74,67 - 64 \cdot \cos φ$	$=$	$22,4$	$+ 64 \cdot \cos φ$
$74,67$	$=$	$64 \cdot \cos φ + 22,4$	$- 22,4$
$52,27$	$=$	$64 \cdot \cos φ$	$: 64$
$\frac{52,27}{64}$	$=$	$\cos φ$

Nachtermin Teil B

Aufgabe B 1

Berechnung der Länge der halben Diagonalen D2B2,

Zeige, dass für den Umfang u der Rauten ABnCDn in Abhängigkeit von φ gilt: u(φ)=10sin⁡(0,5φ)cm

Berechnung von |ABn| mithilfe des Sinus

Berechne den Umfang der Raute AB1CD1 für φ=110∘.

Berechne das zugehörige Maß φ des Winkels CB3A

Aufgabe B 2

Berechne die Länge der Strecken CTn in Abhängigkeit von φ

Berechne das Volumen des zugehörigen Rotationskörpers

Aufgabe B 3

Berechne die Nullstelle der Funktion f1

Zeichne den Graphen zu f1 für x∈[−2,5;10] sowie den Graphen zu f2 für x∈[−1,5;10] in ein Koordinatensystem

Zeichne das Trapez A1B1CD für x=−0,5 und das Trapez A2B2CD für x=6 in das Koordinatensystem zur Aufgabe b) ein

Berechne das Maß des Winkels B2A2D

Bestimme rechnerisch die Werte für b und c

Begründe rechnerisch, weshalb es unter den Trapezen AnBnCD kein Rechteck A3B3CD gibt

Aufgabe B 4

Zeichne das Schrägbild der Pyramide ABCDS, wobei die Strecke AC auf der Schrägbildachse und der Punkt A links vom Punkt C liegen soll

Berechne die Länge der Strecke SC

Berechne das Maß des Winkels MSC

Zeichne die Strecke SE1 sowie den Punkt P1 für φ=40∘ in das Schrägbild zu Aufgabe a) ein

Zeichne die Strecke P1T1 in das Schrägbild zu Aufgabe a) ein

Zeige sodann, dass für die Länge der Strecken MTn in Abhängigkeit von φ gilt: |MTn|(φ)=(7−6⋅cos⁡φ)cm

Gib den zugehörigen Wert für φ an

Zeichne die Pyramide BCDP1 und die Höhe P1F1 in das Schrägbild zu Aufgabe a) ein

Pyramide BCDP1 und die Höhe P1F1 (grün)

Zeige durch Rechnung, dass für das Volumen Vder Pyramiden BCDPn in Abhängigkeit von φ gilt: V(φ)=(74,67−64⋅cos⁡φ)cm3

Berechne den zugehörigen Wert für φ

Bestimme rechnerisch den zugehörigen Wert für φ

Berechnung der Länge der halben Diagonalen $D_{2} B_{2}$ ,

Zeige, dass für den Umfang $u$ der Rauten $A B_{n} C D_{n}$ in Abhängigkeit von $φ$ gilt: $u (φ) = \frac{10}{\sin (0,5 φ)} cm$

Berechnung von $| A B_{n} |$ mithilfe des Sinus

Berechne den Umfang der Raute $A B_{1} C D_{1}$ für $φ = 110^{\circ}$ .

Berechne das zugehörige Maß $φ$ des Winkels $C B_{3} A$

Berechne die Länge der Strecken $C T_{n}$ in Abhängigkeit von $φ$

Berechne die Nullstelle der Funktion $f_{1}$

Zeichne den Graphen zu $f_{1}$ für $x \in [- 2,5; 10]$ sowie den Graphen zu $f_{2}$ für $x \in [- 1,5; 10]$ in ein Koordinatensystem

Zeichne das Trapez $A_{1} B_{1} C D$ für $x = - 0,5$ und das Trapez $A_{2} B_{2} C D$ für $x = 6$ in das Koordinatensystem zur Aufgabe b) ein

Berechne das Maß des Winkels $B_{2} A_{2} D$

Bestimme rechnerisch die Werte für $b$ und $c$

Begründe rechnerisch, weshalb es unter den Trapezen $A_{n} B_{n} C D$ kein Rechteck $A_{3} B_{3} C D$ gibt

Zeichne das Schrägbild der Pyramide $A B C D S$ , wobei die Strecke $A C$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $C$ liegen soll

Berechne die Länge der Strecke $S C$

Berechne das Maß des Winkels $M S C$

Zeichne die Strecke $S E_{1}$ sowie den Punkt $P_{1}$ für $φ = 40^{\circ}$ in das Schrägbild zu Aufgabe a) ein

Zeichne die Strecke $P_{1} T_{1}$ in das Schrägbild zu Aufgabe a) ein

Zeige sodann, dass für die Länge der Strecken $M T_{n}$ in Abhängigkeit von $φ$ gilt: $| M T_{n} | (φ) = (7 - 6 \cdot \cos φ) cm$

Gib den zugehörigen Wert für $φ$ an

Zeichne die Pyramide $B C D P_{1}$ und die Höhe $P_{1} F_{1}$ in das Schrägbild zu Aufgabe a) ein

Pyramide $B C D P_{1}$ und die Höhe $P_{1} F_{1}$ (grün)

Zeige durch Rechnung, dass für das Volumen $V$ der Pyramiden $B C D P_{n}$ in Abhängigkeit von $φ$ gilt: $V (φ) = (74,67 - 64 \cdot \cos φ) {cm}^{3}$

Berechne den zugehörigen Wert für $φ$

Bestimme rechnerisch den zugehörigen Wert für $φ$