Teil B

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Aufgabe B1

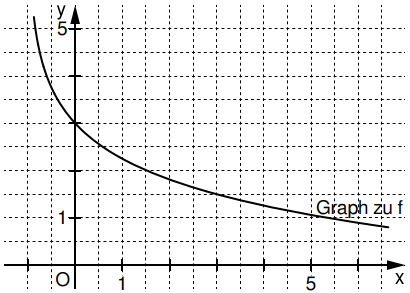
Gegeben ist die Funktion $f$ mit der Gleichung $y = - 0,75 \cdot \log_{2} (x + 1) + 3 (x, y \in ℝ)$ .

Im Koordinatensystem ist der Graph der Funktion $f$ bereits eingezeichnet.

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

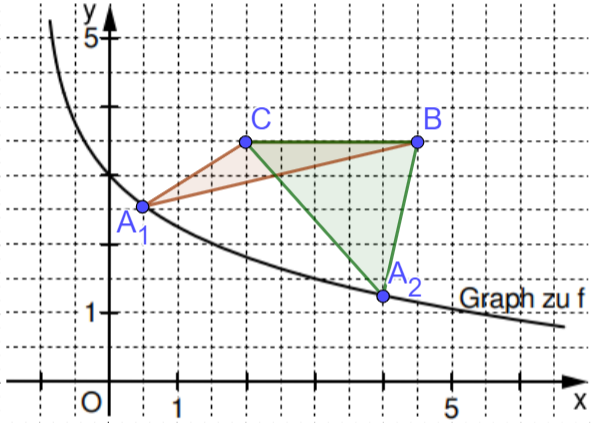
Punkte $A_{n} (x | - 0,75 \cdot \log_{2} (x + 1) + 3)$ auf dem Graphen zu $f$ bilden zusammen mit den

Punkten $B (4,5 | 3,5)$ und $C (2 | 3,5)$ Dreiecke $A_{n} B C$ .

Ergänzen Sie im Koordinatensystem in der Zeichnung zur Aufgabenstellung die Dreiecke $A_{1} B C$ für $x = 0,5$ und $A_{2} B C$ für $x = 4$ .

Ermitteln Sie sodann rechnerisch, für welche Belegungen von $x$ es Dreiecke $A_{n} B C$

gibt. (4,5 P)

Das Dreieck $A_{3} B C$ ist gleichschenklig mit der Basis $B C$ .
Bestimmen Sie rechnerisch die Koordinaten des Punktes $A_{3}$ . (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Strecke
Bestimme rechnerisch die Koordinaten des Punktes $A_{3}$
Berechne die Mitte der Strecke $B C$ :
$x_{A_{3}} = \frac{2 + 4,5}{2} = 3,25$
Demnach gilt:
$A_{3} (3,25 | f (3,25)$ mit $f (3,25) = - 0,75 \cdot \log_{2} (3,25 + 1) + 3 \approx 1,43$
$\Rightarrow A_{3} (3,25 | 1,43)$
Berechne die Mitte der Strecke $B C$ $\Rightarrow x_{1}$
Berechne dann $A_{3} (x_{1} | f (x_{1})$ .

2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe B2
Gegeben sind das Trapez $A B C D$ und Punkte $P_{n}$ auf der Diagonalen $B D$ (siehe Zeichnung). Die Punkte $C, D$ und $P_{n}$ legen Dreiecke $C D P_{n}$ fest. Die Winkel $D C P_{n}$ haben das Maß $φ$ mit $φ \in] 0^{\circ}; {51,34}^{\circ}]$ .
Es gilt: $| A B | = 7 cm$ ; $| C D | = 11 cm$ ; $| A D | = 5 cm$ ; $∢ A D C = 90^{\circ}$ ; $A B ∥ C D$ .
Die Zeichnung zeigt das Dreieck $C D P_{1}$ für $φ = 20^{\circ}$ .
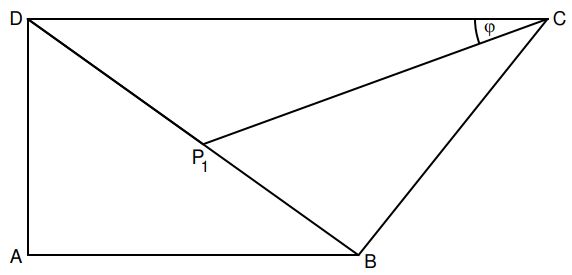
Zeigen Sie rechnerisch, dass für die Länge der Strecken $D P_{n}$ in Abhängigkeit von $φ$ gilt: $| D P_{n} | (φ) = \frac{11 \cdot \sin φ}{\sin ({35,54}^{\circ} + φ)} cm$ .
Berechnen Sie sodann die Länge der Strecke $D P_{1}$ .
Runden Sie auf zwei Stellen nach dem Komma.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinussatz und Kosinussatz im allgemeinen Dreieck
Zeige rechnerisch, dass für die Länge der Strecken $D P_{n}$ in Abhängigkeit von $φ$ gilt: $| D P_{n} | (φ) = \frac{11 \cdot \sin φ}{\sin ({35,54}^{\circ} + φ)} cm$
In beliebigen Dreiecken gilt der Sinussatz:
$\frac{a}{\sin (α)} = \frac{b}{\sin (β)} = \frac{c}{\sin (γ)}$
eingezeichnetes Dreieck mit Winkeln
Angewandt auf das Dreieck $C D P_{n}$ folgt:
$\frac{| D P_{n} |}{\sin φ} = \frac{| C D |}{\sin ∢ C P_{n} D}$
Weiterhin gilt: $∢ C P_{n} D = 180^{\circ} - (∢ B D C + φ)$
Für den Winkel $∢ B D C$ gilt: $∢ B D C = 90^{\circ} - ∢ A D B$
Der Winkel $∢ A D B$ befindet sich im rechtwinkligen Dreieck $A B D$ , sodass er berechnet werden kann.
$\tan ∢ A D B = \frac{| A B |}{| A D |} = \frac{7}{5} = 1,4 \Rightarrow ∢ A D B = \tan^{- 1} (1,4) \approx {54,46}^{\circ}$
Dann folgt für den Winkel $∢ B D C = 90^{\circ} - ∢ A D B = 90^{\circ} - {54,46}^{\circ} = {35,54}^{\circ}$
Nun kann auch der Winkel $∢ C P_{n} D = 180^{\circ} - (∢ B D C + φ)$ angegeben werden:
$∢ C P_{n} D = 180^{\circ} - ({35,54}^{\circ} + φ)$
Für den Ansatz mit dem Sinussatz erhält man nun:
$\frac{| D P_{n} |}{\sin φ} = \frac{| C D |}{\sin ∢ C P_{n} D} = \frac{| C D |}{\sin (180^{\circ} - ({35,54}^{\circ} + φ))}$
Wegen $\sin (180^{\circ} - α) = \sin α$ kann die rechte Seite der Gleichung noch umgeformt werden:
$\frac{| D P_{n} |}{\sin φ} = \frac{| C D |}{\sin (180^{\circ} - ({35,54}^{\circ} + φ))} = \frac{| C D |}{\sin ({35,54}^{\circ} + φ))}$
Aufgelöst nach $| D P_{n} |$ erhält man:
$| D P_{n} | = \frac{| C D | \cdot \sin φ}{\sin ({35,54}^{\circ} + φ))}$
Setzt man nun noch $| C D | = 11 cm$ ein, dann folgt:
$| D P_{n} | = \frac{11 cm \cdot \sin φ}{\sin ({35,54}^{\circ} + φ))} \Rightarrow | D P_{n} | (φ) = \frac{11 \cdot \sin φ}{\sin ({35,54}^{\circ} + φ)} cm$
Berechne die Länge der Strecke $D P_{1}$
Der Winkel $φ$ ist hier $20^{\circ}$ .
Eingesetzt in $| D P_{n} | (φ) \Rightarrow | D P_{1} | (20^{\circ}) = \frac{11 \cdot \sin 20^{\circ}}{\sin ({35,54}^{\circ} + 20^{\circ})} \approx 4,56$
Die Länge der Strecke $D P_{1}$ beträgt rund $4,56 cm$ .
Teil 1
Wende den Sinussatz auf das Dreieck $C D P_{n}$ an.
Benutze zur Berechnung des fehlenden Winkels auch das rechtwinklige Dreieck $A B D$ .
Teil 2
Setze den Winkel $φ = 20^{\circ}$ in $| D P_{1} | (φ)$ ein.

Das Dreieck $C D P_{2}$ ist gleichschenklig mit der Basis $C D$ .
Ergänzen Sie das Dreieck $C D P_{2}$ in der Zeichnung zur Aufgabenstellung.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichschenkliges Dreieck
Ergänze das Dreieck $C D P_{2}$ in der Zeichnung zur Aufgabenstellung
Das Dreieck $C D P_{2}$ ist gleichschenklig mit der Basis $C D$ .
Errichte die Mittelsenkrechte über der Strecke $C D$ .
Die Mittelsenkrechte schneidet die Strecke $B D$ in Punkt $P_{2}$ .
Siehe Zeichnung:
Das Dreieck $C D P_{2}$ ist gleichschenklig.
Errichte die Mittelsenkrechte über der Strecke $C D$ . Sie schneidet die Strecke $B D$ in Punkt $P_{2}$ .

Aufgabe B 3

Der Punkt $A (0 | 0)$ ist gemeinsamer Eckpunkt von Rechtecken $A B_{n} C_{n} D_{n}$ .

Die Eckpunkte $B_{n} (x | - 0,25 x + 6)$ liegen auf der Geraden $g$ mit der Gleichung

$y = - 0,25 x + 6$ $(x, y \in ℝ)$ . Es gilt: $| B_{n} C_{n} | = \frac{1}{2} | A B_{n} |$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Zeichnen Sie die Gerade $g$ sowie die Rechtecke $A B_{1} C_{1} D_{1}$ für $x = - 1$ und $A B_{2} C_{2} D_{2}$ für $x = 7$ in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit $1 cm$ ; $- 5 \leq x \leq 8; - 1 \leq y \leq 8$ (2,5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
Zeichne die Gerade $g$ sowie die Rechtecke $A B_{1} C_{1} D_{1}$ für $x = - 1$ und $A B_{2} C_{2} D_{2}$ für $x = 7$ in ein Koordinatensystem
Zeichne die Gerade $g$ mit der Gleichung $y = - 0,25 x + 6$ in ein Koordinatensystem.
Rechteck $A B_{1} C_{1} D_{1}$
Der Punkt $B_{1} (- 1 | f (- 1))$ (mit $f (x) = - 0,25 x + 6$ ) liegt auf der Geraden $g$ .
Miss die Länge der Strecke $A B_{1}$ . Trage wegen $| B_{n} C_{n} | = \frac{1}{2} | A B_{n} |$ die Hälfte der gemessenen Strecke sowohl im Punkt $B_{1}$ als auch im Punkt $A$ senkrecht zur Strecke $A B_{1}$ ab. Man erhält die Punkte $C_{1}$ und $D_{1}$ . Verbinde $C_{1}$ mit $D_{1}$ .
Rechteck $A B_{2} C_{2} D_{2}$
Verfahre entsprechend mit dem Punkt $B_{2} (7 | f (7))$ .
Zeichne die Gerade $g$ in ein Koordinatensystem ein.
Rechteck $A B_{1} C_{1} D_{1}$ für $x = - 1$ .
Der Punkt $B_{1} (- 1 | f (- 1))$ liegt auf der Geraden $g$ .
Miss die Länge der Strecke $A B_{1}$ . Trage die Hälfte der gemessenen Strecke sowohl im Punkt $B_{1}$ als auch im Punkt $A$ senkrecht zur Strecke $A B_{1}$ ab.
Man erhält die Punkte $C_{1}$ und $D_{1}$ . Verbinde $C_{1}$ mit $D_{1}$ .
Verfahre für das Rechteck $A B_{2} C_{2} D_{2}$ für $x = 7$ entsprechend.
Ermitteln Sie rechnerisch die Koordinaten der Punkte $C_{n}$ in Abhängigkeit von der
Abszisse $x$ der Punkte $B_{n}$ .
$[$ Ergebnis: $C_{n} (1,13 x - 3 | 0,25 x + 6)$ $]$ (3,5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Drehung mittels Matrizen
Ermittle rechnerisch die Koordinaten der Punkte $C_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$
Es gilt gemäß Zeichnung: $\vec{O C_{n}} = \vec{O B_{n}} + \vec{B_{n} C_{n}}$
Dabei ist $\vec{B_{n} C_{n}} = \vec{O D_{n}}$ .
Der Vektor $\vec{O B_{n}}$ wird zunächst um $90^{\circ}$ um den Ursprung gedreht. Dieser Vektor wird dann durch zentrische Streckung mit dem Streckungsfaktor $k = 0,5$ gestreckt. Ergebnis ist der Vektor $\vec{O D_{n}}$ .
$\vec{O B_{n}} \overset{\overset{}{O, φ = 90^{\circ}}}{\to} \vec{O B_{n}^{'}} \overset{\overset{}{O, k = 0,5}}{\to} \vec{O D_{n}}$
Für die Drehung um $φ = 90^{\circ}$ um den Ursprung gilt:
$(\begin{array}{c} x^{'} \\ y^{'} \end{array}) = (\begin{array}{cc} \cos 90^{\circ} & - \sin 90^{\circ} \\ \sin 90^{\circ} & \cos 90^{\circ} \end{array}) \cdot (\begin{array}{c} x \\ y \end{array}) = (\begin{array}{cc} 0 & - 1 \\ 1 & 0 \end{array}) \cdot (\begin{array}{c} x \\ y \end{array}) = (\begin{array}{c} - y \\ x \end{array})$
Dann folgt für $x \in ℝ$ :
$(\begin{array}{c} x \\ - 0,25 x + 6 \end{array}) \overset{\overset{}{O, φ = 90^{\circ}}}{\to} (\begin{array}{c} - (- 0,25 x + 6) \\ x \end{array}) = (\begin{array}{c} 0,25 x - 6 \\ x \end{array})$
$\Rightarrow (\begin{array}{c} 0,25 x - 6 \\ x \end{array}) \overset{\overset{}{O, k = 0,5}}{\to} 0,5 \cdot (\begin{array}{c} 0,25 x - 6 \\ x \end{array}) = (\begin{array}{c} 0,13 x - 3 \\ 0,5 x \end{array})$
Somit ist $\vec{O D_{n}} = (\begin{array}{c} 0,13 x - 3 \\ 0,5 x \end{array})$ .
Nun kann der Vektor $\vec{O C_{n}}$ berechnet werden:
$\vec{O C_{n}} = \vec{O B_{n}} + \vec{B_{n} C_{n}}$
$\vec{O C_{n}} (x) = (\begin{array}{c} x \\ - 0,25 x + 6 \end{array}) + (\begin{array}{c} 0,13 x - 3 \\ 0,5 x \end{array}) = (\begin{array}{c} 1,13 x - 3 \\ 0,25 x + 6 \end{array})$
Die Koordinaten der Punkte $C_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ lauten $C_{n} (1,13 x - 3 | 0,25 x + 6)$ .
Es gilt gemäß Zeichnung $\vec{O C_{n}} = \vec{O B_{n}} + \vec{B_{n} C_{n}}$ , dabei ist $\vec{B_{n} C_{n}} = \vec{O D_{n}}$ .
Der Vektor $\vec{O B_{n}}$ wird zunächst um $90^{\circ}$ um den Ursprung gedreht. Dieser Vektor wird dann durch zentrische Streckung mit dem Streckungsfaktor $k = 0,5$ gestreckt.
Ergebnis ist der Vektor $\vec{O D_{n}}$ . Mit diesem Vektor kann der Vektor $\vec{O C_{n}}$ berechnet werden.
Zeigen Sie, dass sich der Umfang $u$ der Rechtecke $A B_{n} C_{n} D_{n}$ in Abhängigkeit von der
Abszisse $x$ der Punkte $B_{n}$ wie folgt darstellen lässt:
$u (x) = \sqrt{9,54 x^{2} - 27 x + 324} LE$ . (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Rechteck
Zeige, dass sich der Umfang $u$ der Rechtecke $A B_{n} C_{n} D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ wie folgt darstellen lässt: $u (x) = \sqrt{9,54 x^{2} - 27 x + 324} LE$
Es gilt: $| B_{n} C_{n} | = \frac{1}{2} | A B_{n} |$
Dann folgt für den Umfang $u$ für $x \in ℝ$ :
$u = 2 \cdot (| A B_{n} | + | B_{n} C_{n} |) = 2 \cdot (| A B_{n} | + 0,5 \cdot | A B_{n} |) = 3 \cdot | A B_{n} |$
$\vec{A B_{n}} = (\begin{array}{c} x \\ - 0,25 x + 6 \end{array}) \Rightarrow | \vec{A B_{n}} | (x) = \sqrt{x^{2} + (- 0,25 x + 6)^{2}}$
$| \vec{A B_{n}} | (x) = \sqrt{x^{2} + \frac{1}{16} x^{2} - 3 x + 36} = \sqrt{1,06 x^{2} - 3 x + 36} LE$
$\Rightarrow u (x) = 3 \cdot | A B_{n} | = 3 \cdot \sqrt{1,06 x^{2} - 3 x + 36} = \sqrt{9 \cdot (1,06 x^{2} - 3 x + 36)}$
$u (x) = \sqrt{9 \cdot (1,06 x^{2} - 3 x + 36)} = \sqrt{9,54 x^{2} - 27 x + 324} LE$
Damit ist gezeigt, dass sich der Umfang $u$ der Rechtecke $A B_{n} C_{n} D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ wie folgt darstellen lässt:
$u (x) = \sqrt{9,54 x^{2} - 27 x + 324} LE$
Es gilt: $| B_{n} C_{n} | = \frac{1}{2} | A B_{n} |$
Für den Umfang $u$ folgt dann $u = 2 \cdot (| A B_{n} | + | B_{n} C_{n} |)$
Berechne $| \vec{A B_{n}} | (x)$ und damit dann $u (x)$ .
Der Punkt $C_{3}$ liegt auf der y–Achse.
Berechnen Sie den Umfang des Rechtecks $A B_{3} C_{3} D_{3}$ . (2,5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: y-Achsenabschnitt
Berechne den Umfang des Rechtecks $A B_{3} C_{3} D_{3}$
Der Punkt $C_{3} (1,13 x - 3 | 0,25 x + 6)$ liegt auf der y–Achse.
Deshalb gilt für $x_{C_{3}}$ :
$x_{C_{3}} = 0 \Rightarrow 1,13 x - 3 = 0 \Rightarrow x = \frac{3}{1,13} \approx 2,65$
$L = {2,65}$
Setze $x = 2,65$ in $u (x)$ ein:
$u (2,65) = \sqrt{9,54 \cdot (2,65)^{2} - 27 \cdot 2,65 + 324} = \sqrt{319,44} \approx 17,87$
Der Umfang des Rechtecks $A B_{3} C_{3} D_{3}$ beträgt rund $17,87 LE$ .
Der Punkt $C_{3} (1,13 x - 3 | 0,25 x + 6)$ liegt auf der y–Achse.
Deshalb gilt für $x_{C_{3}}$ : $x_{C_{3}} = 0 \Rightarrow x_{1}$
Setze $x_{1}$ in $u (x)$ ein.

Für den Punkt $C_{4}$ gilt: $C_{4} \in g$ .

Begründen Sie, warum das zugehörige Rechteck $A B_{4} C_{4} D_{4}$ den minimalen Umfang

hat.

Bestimmen Sie sodann den minimalen Umfang sowie die zugehörige Belegung für $x$ .

(4 P)

Aufgabe B 4

Die Diagonalen $A C$ und $B D$ der Raute $A B C D$ schneiden sich im Punkt $M$ .

Die Raute $A B C D$ ist die Grundfläche der Pyramide $A B C D S$ mit der Höhe $M S$ .

Es gilt: $| A C | = 12 cm$ ; $| B D | = 8 cm$ ; $| C S | = 9,5 cm$ .

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

Zeichnen Sie das Schrägbild der Pyramide $A B C D S$ , wobei die Strecke $A C$ auf der
Schrägbildachse und der Punkt $A$ links vom Punkt $C$ liegen soll.
Für die Zeichnung gilt: $q = \frac{1}{2}; ω = 45^{\circ}$
Berechnen Sie sodann das Maß des Winkels $S C A$ und die Länge der Strecke $M S$ .
$[$ Teilergebnisse: $∢ S C A = {50,83}^{\circ}; | M S | = 7,37 cm]$ (4 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder zeichnen
Zeichne das Schrägbild der Pyramide $A B C D S$ , wobei die Strecke $A C$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $C$ liegen soll, mit $q = \frac{1}{2}; ω = 45^{\circ}$
Es gilt: $| A C | = 12 cm$ ; $| B D | = 8 cm$ ; $| C S | = 9,5 cm$ .
Wegen $q = \frac{1}{2}$ ist die Strecke in der Zeichnung nur $| B D | = 4 cm$ lang.
Pyramide $A B C D S$
Berechne das Maß des Winkels $S C A$ und die Länge der Strecke $M S$
Maß des Winkels $S C A$
Betrachte das rechtwinklige Dreieck $S C M$ . Hier gilt:
$\cos ∢ S C A = \frac{0,5 \cdot A C}{S C} = \frac{0,5 \cdot 12}{9,5} \approx 0,6316$
$\Rightarrow ∢ S C A = \cos^{- 1} (0,6316) \approx {50,83}^{\circ}$
Länge der Strecke $M S$
Betrachte das rechtwinklige Dreieck $S C M$ .
Benutze den Satz des Pythagoras:
$| M S |^{2} = {C S}^{2} - (0,5 \cdot A C)^{2} \Rightarrow | M S | = \sqrt{{9,5}^{2} - (0,5 \cdot 12)^{2}} \approx 7,37$
Das Maß des Winkels $S C A$ beträgt rund ${50,83}^{\circ}$ und die Länge der Strecke $M S$ beträgt rund $7,37 cm$ .
Teil 1
Zeichne die Pyramide, beachte für die Strecke $B D$ : $q = \frac{1}{2}$ und $ω = 45^{\circ}$
Teil 2
Betrachte das rechtwinklige Dreieck $S C M$ .
Winkelberechnung: Benutze den $\cos$ .
Streckenlänge: Benutze den Satz des Pythagoras.
Punkte $P_{n}$ liegen auf der Strecke $C S$ . Die Winkel $C A P_{n}$ haben das Maß $φ$ mit
$φ \in] 0^{\circ}; {50,83}^{\circ}]$ . Die Punkte $P_{n}$ sind zusammen mit den Punkten $A$ und $C$ die
Eckpunkte von Dreiecken $A C P_{n}$ . Die Dreiecke $A C P_{n}$ sind Grundflächen von
Pyramiden mit der Spitze $B$ .
Zeichnen Sie die Pyramide $A C P_{1} B$ für $φ = 35^{\circ}$ in das Schrägbild zu Aufgabe a) ein. (1 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Winkel konstruieren
Zeichne die Pyramide $A C P_{1} B$ für $φ = 35^{\circ}$ in das Schrägbild zu Aufgabe a) ein
Pyramide $A C P_{1} B$
Zeichne an die Strecke $A C$ im Punkt $A$ den Winkel $φ = 35^{\circ}$ . Der freie Schenkel schneidet die Strecke $C S$ im Punkt $P_{1}$ .

Zeigen Sie, dass für die Länge der Strecken $A P_{n}$ in Abhängigkeit von $φ$ gilt:

$| A P_{n} | (φ) = \frac{9,30}{\sin (φ + {50,83}^{\circ})} cm$ .

Für die Strecke $A P_{2}$ gilt: $| A P_{2} | = 10 cm$ .

Berechnen Sie den zugehörigen Wert von $φ$ . (3,5 P)

Zeigen Sie, dass für das Volumen $V$ der Pyramiden $A C P_{n} B$ in Abhängigkeit von $φ$ gilt:
$V (φ) = \frac{74,40 \cdot \sin φ}{\sin (φ + {50,83}^{\circ})} {cm}^{3}$ .
Berechnen Sie sodann, um wie viel Prozent das Volumen der Pyramide $A C P_{1} B$ kleiner
ist als das Volumen der Pyramide $A B C D S$ . (5 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
Zeige, dass für das Volumen $V$ der Pyramiden $A C P_{n} B$ in Abhängigkeit von $φ$ gilt: $V (φ) = \frac{74,40 \cdot \sin φ}{\sin (φ + {50,83}^{\circ})} {cm}^{3}$
Die Abbildung ist in der Aufgabenstellung nicht gefordert. Sie dient nur zur Veranschaulichung.
Pyramide $A C P_{n} B$
$V_{P} = \frac{1}{3} \cdot G \cdot h_{P}$
Die Grundfläche der Pyramide ist eine halbe Raute.
$G = \frac{1}{2} \cdot A_{Raute} = \frac{1}{2} \cdot (\frac{1}{2} \cdot | A C | \cdot | B D |) = \frac{1}{4} \cdot 12 \cdot 8 = 24 {cm}^{2}$
Für die Höhe dieser Pyramide (siehe Abbildung) gilt:
$\sin φ = \frac{h_{P}}{| A P_{n} |}$
$\Rightarrow h_{P} = \sin φ \cdot | A P_{n} | = \sin φ \cdot \frac{9,30 cm}{\sin (φ + {50,83}^{\circ})} = \frac{9,30 \cdot \sin φ}{\sin (φ + {50,83}^{\circ})} cm$
$V (φ) = \frac{1}{3} \cdot 24 \cdot \frac{9,30 \cdot \sin φ}{\sin (φ + {50,83}^{\circ})} = \frac{74,40 \cdot \sin φ}{\sin (φ + {50,83}^{\circ})} {cm}^{3}$
Für das Volumen $V$ der Pyramiden $A C P_{n} B$ in Abhängigkeit von $φ$ gilt:
$V (φ) = \frac{74,40 \cdot \sin φ}{\sin (φ + {50,83}^{\circ})} {cm}^{3}$
Berechne, um wie viel Prozent das Volumen der Pyramide $A C P_{1} B$ kleiner ist als das Volumen der Pyramide $A B C D S$
Zum Winkel $35^{\circ}$ gehört das Volumen:
$V (35^{\circ}) = \frac{74,40 \cdot \sin 35^{\circ}}{\sin (35^{\circ} + {50,83}^{\circ})} \approx 42,79 {cm}^{3}$
$V_{A B C D S} = \frac{1}{3} \cdot G \cdot h_{P}$
Die Grundfläche der Pyramide ist eine Raute.
$G = A_{Raute} = \frac{1}{2} \cdot | A C | \cdot | B D | = \frac{1}{2} \cdot 12 \cdot 8 = 48 {cm}^{2}$
Die Höhe dieser Pyramide ist $h_{P} = | M S | = 7,37 cm$ (siehe Aufgabe a).
Dann folgt:
$V_{A B C D S} = \frac{1}{3} \cdot 48 \cdot 7,37 = 117,92 {cm}^{3}$
Berechne das Verhältnis:
$\frac{117,92 - 42,79}{117,92} \approx 0,6371$ oder $63,71 %$
Das Volumen der Pyramide $A C P_{1} B$ ist um rund $63,71 %$ kleiner als das Volumen der Pyramide $A B C D S$ .
Teil 1
Das Pyramidenvolumen berechnet man mit $V_{P} = \frac{1}{3} \cdot G \cdot h_{P}$ .
Die Grundfläche der Pyramide ist eine halbe Raute.
Für die Höhenberechnung der Pyramide benutzt man den $\sin$ .
Teil 2
Berechne mit der erhaltenen Volumenformel das Volumen $V (35^{\circ})$ .
Berechne das Volumen der gesamten Pyramide $V_{P}$ . (Die Grundfläche der Pyramide ist eine Raute.)
Bilde dann das Verhältnis: $\frac{V_{P} - V (35^{\circ})}{V_{P}}$
Die Pyramide $A C P_{3} B$ hat dasselbe Volumen wie die Pyramide $A P_{3} S B$ .
In welchem Verhältnis steht das Volumen der Pyramide $A C P_{3} B$ zum Volumen der
Pyramide $A B C D S$ ? Begründen Sie. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Pyramide
In welchem Verhältnis steht das Volumen der Pyramide $A C P_{3} B$ zum Volumen der Pyramide $A B C D S$ ? Begründe
Die Abbildung ist in der Aufgabenstellung nicht gefordert. Sie dient nur zur Veranschaulichung.
Pyramiden $A P_{3} S B$ und $A C P_{3} B$
Die grüne $(A P_{3} S B)$ und die braune $(A C P_{3} B)$ Pyramide sind zusammen genau halb so groß wie die Pyramide $A B C D S$ .
$\Rightarrow V_{A C P_{3} B} + V_{A P_{3} S B} = 0,5 \cdot V_{A B C D S}$
Die Pyramide $A C P_{3} B$ hat dasselbe Volumen wie die Pyramide $A P_{3} S B$ .
$\Rightarrow V_{A C P_{3} B} = V_{A P_{3} S B}$
Es folgt:
$2 \cdot V_{A P_{3} S B} = 0,5 \cdot V_{A B C D S} \Rightarrow V_{A P_{3} S B} = 0,25 \cdot V_{A B C D S}$
Das Volumen der Pyramide $A C P_{3} B$ beträgt $\frac{1}{4}$ des Volumens der Pyramide $A B C D S$ .
Es gilt: $V_{A C P_{3} B} + V_{A P_{3} S B} = 0,5 \cdot V_{A B C D S}$
Weiterhin gilt: $V_{A C P_{3} B} = V_{A P_{3} S B}$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$3,5$	$=$	$- 0,75 \cdot \log_{2} (x + 1) + 3$	$- 3$
	↓	Löse nach $x$ auf.
$0,5$	$=$	$- 0,75 \cdot \log_{2} (x + 1)$	$: (- 0,75)$
$\frac{0,5}{- 0,75}$	$=$	$\log_{2} (x + 1)$
	↓	Vereinfache.
$- \frac{2}{3}$	$=$	$\log_{2} (x + 1)$	$2^{()}$
	↓	Löse den Logarithmus auf
$2^{- \frac{2}{3}}$	$=$	$x + 1$	$- 1$
$2^{- \frac{2}{3}} - 1$	$=$	$x$
$- 0,37$	$\approx$	$x$

	$9,54 x^{2} - 27 x + 324$
	↓ Klammere $9,54$ aus.
$=$	$9,54 (x^{2} - 2,83 x + 33,96)$
	↓ Bilde die quadratische Ergänzung.
$=$	$9,54 (x^{2} - 2,83 x + {(\frac{2,83}{2})}^{2} - {(\frac{2,83}{2})}^{2} + 33,96)$
	↓ Fasse zusammen.
$=$	$9,54 ((x - 1,42)^{2} - 2 + 33,96)$
	↓ Löse die Klammer auf.
$=$	$9,54 (x - 1,42)^{2} + 304,90$

$10$	$=$	$\frac{9,30}{\sin (φ + {50,83}^{\circ})}$	$\cdot \sin (φ + {50,83}^{\circ})$
	↓	Löse nach $φ$ auf.
$10 \cdot \sin (φ + {50,83}^{\circ})$	$=$	$9,30$	$: 10$
$\sin (φ + {50,83}^{\circ})$	$=$	$0,93$	$\sin^{- 1}$
$φ + {50,83}^{\circ}$	$=$	$\sin^{- 1} (0,93)$
$φ + {50,83}^{\circ}$	$=$	${68,43}^{\circ}$	$- {50,83}^{\circ}$
$φ$	$=$	${17,60}^{\circ}$

Teil B

Aufgabe B1

Ergänze im Koordinatensystem in der Zeichnung zur Aufgabenstellung die Dreiecke $A_{1} B C$ für $x = 0,5$ und $A_{2} B C$ für $x = 4$

Ermittle sodann rechnerisch, für welche Belegungen von $x$ es Dreiecke $A_{n} B C$ gibt

Bestimme rechnerisch die Koordinaten des Punktes $A_{3}$

Aufgabe B2

Zeige rechnerisch, dass für die Länge der Strecken $D P_{n}$ in Abhängigkeit von $φ$ gilt: $| D P_{n} | (φ) = \frac{11 \cdot \sin φ}{\sin ({35,54}^{\circ} + φ)} cm$

Berechne die Länge der Strecke $D P_{1}$

Ergänze das Dreieck $C D P_{2}$ in der Zeichnung zur Aufgabenstellung

Aufgabe B 3

Zeichne die Gerade $g$ sowie die Rechtecke $A B_{1} C_{1} D_{1}$ für $x = - 1$ und $A B_{2} C_{2} D_{2}$ für $x = 7$ in ein Koordinatensystem

Ermittle rechnerisch die Koordinaten der Punkte $C_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$

Zeige, dass sich der Umfang $u$ der Rechtecke $A B_{n} C_{n} D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ wie folgt darstellen lässt: $u (x) = \sqrt{9,54 x^{2} - 27 x + 324} LE$

Berechne den Umfang des Rechtecks $A B_{3} C_{3} D_{3}$

Begründe, warum das zugehörige Rechteck $A B_{4} C_{4} D_{4}$ den minimalen Umfang hat

Bestimme sodann den minimalen Umfang sowie die zugehörige Belegung für $x$

Aufgabe B 4

Zeichne das Schrägbild der Pyramide $A B C D S$ , wobei die Strecke $A C$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $C$ liegen soll, mit $q = \frac{1}{2}; ω = 45^{\circ}$

Pyramide $A B C D S$

Berechne das Maß des Winkels $S C A$ und die Länge der Strecke $M S$

Zeichne die Pyramide $A C P_{1} B$ für $φ = 35^{\circ}$ in das Schrägbild zu Aufgabe a) ein

Zeige, dass für die Länge der Strecken $A P_{n}$ in Abhängigkeit von $φ$ gilt: $| A P_{n} | (φ) = \frac{9,30}{\sin (φ + {50,83}^{\circ})} cm$

Berechne den zugehörigen Wert von $φ$

Zeige, dass für das Volumen $V$ der Pyramiden $A C P_{n} B$ in Abhängigkeit von $φ$ gilt: $V (φ) = \frac{74,40 \cdot \sin φ}{\sin (φ + {50,83}^{\circ})} {cm}^{3}$

Berechne, um wie viel Prozent das Volumen der Pyramide $A C P_{1} B$ kleiner ist als das Volumen der Pyramide $A B C D S$

In welchem Verhältnis steht das Volumen der Pyramide $A C P_{3} B$ zum Volumen der Pyramide $A B C D S$ ? Begründe

Teil B

Aufgabe B1

Ergänze im Koordinatensystem in der Zeichnung zur Aufgabenstellung die Dreiecke A1BC für x=0,5 und A2BC für x=4

Ermittle sodann rechnerisch, für welche Belegungen von x es Dreiecke AnBC gibt

Bestimme rechnerisch die Koordinaten des Punktes A3

Aufgabe B2

Zeige rechnerisch, dass für die Länge der Strecken DPn in Abhängigkeit von φ gilt: |DPn|(φ)=11⋅sin⁡φsin⁡(35,54∘+φ)cm

Berechne die Länge der Strecke DP1

Ergänze das Dreieck CDP2 in der Zeichnung zur Aufgabenstellung

Aufgabe B 3

Zeichne die Gerade g sowie die Rechtecke AB1C1D1 für x=−1 und AB2C2D2 für x=7 in ein Koordinatensystem

Ermittle rechnerisch die Koordinaten der Punkte Cn in Abhängigkeit von der Abszisse x der Punkte Bn

Zeige, dass sich der Umfang u der Rechtecke ABnCnDn in Abhängigkeit von der Abszisse x der Punkte Bn wie folgt darstellen lässt: u(x)=9,54x2−27x+324LE

Berechne den Umfang des Rechtecks AB3C3D3

Begründe, warum das zugehörige Rechteck AB4C4D4 den minimalen Umfang hat

Bestimme sodann den minimalen Umfang sowie die zugehörige Belegung für x

Aufgabe B 4

Zeichne das Schrägbild der Pyramide ABCDS, wobei die Strecke AC auf der Schrägbildachse und der Punkt A links vom Punkt C liegen soll, mit q=12; ω=45∘

Pyramide ABCDS

Berechne das Maß des Winkels SCA und die Länge der Strecke MS

Zeichne die Pyramide ACP1B für φ=35∘ in das Schrägbild zu Aufgabe a) ein

Zeige, dass für die Länge der Strecken APn in Abhängigkeit von φ gilt: |APn|(φ)=9,30sin⁡(φ+50,83∘)cm

Berechne den zugehörigen Wert von φ

Zeige, dass für das Volumen Vder Pyramiden ACPnB in Abhängigkeit von φ gilt: V(φ)=74,40⋅sin⁡φsin⁡(φ+50,83∘)cm3

Berechne, um wie viel Prozent das Volumen der Pyramide ACP1B kleiner ist als das Volumen der Pyramide ABCDS

In welchem Verhältnis steht das Volumen der Pyramide ACP3B zum Volumen der Pyramide ABCDS? Begründe

Ergänze im Koordinatensystem in der Zeichnung zur Aufgabenstellung die Dreiecke $A_{1} B C$ für $x = 0,5$ und $A_{2} B C$ für $x = 4$

Ermittle sodann rechnerisch, für welche Belegungen von $x$ es Dreiecke $A_{n} B C$ gibt

Bestimme rechnerisch die Koordinaten des Punktes $A_{3}$

Zeige rechnerisch, dass für die Länge der Strecken $D P_{n}$ in Abhängigkeit von $φ$ gilt: $| D P_{n} | (φ) = \frac{11 \cdot \sin φ}{\sin ({35,54}^{\circ} + φ)} cm$

Berechne die Länge der Strecke $D P_{1}$

Ergänze das Dreieck $C D P_{2}$ in der Zeichnung zur Aufgabenstellung

Zeichne die Gerade $g$ sowie die Rechtecke $A B_{1} C_{1} D_{1}$ für $x = - 1$ und $A B_{2} C_{2} D_{2}$ für $x = 7$ in ein Koordinatensystem

Ermittle rechnerisch die Koordinaten der Punkte $C_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$

Zeige, dass sich der Umfang $u$ der Rechtecke $A B_{n} C_{n} D_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ wie folgt darstellen lässt: $u (x) = \sqrt{9,54 x^{2} - 27 x + 324} LE$

Berechne den Umfang des Rechtecks $A B_{3} C_{3} D_{3}$

Begründe, warum das zugehörige Rechteck $A B_{4} C_{4} D_{4}$ den minimalen Umfang hat

Bestimme sodann den minimalen Umfang sowie die zugehörige Belegung für $x$

Zeichne das Schrägbild der Pyramide $A B C D S$ , wobei die Strecke $A C$ auf der Schrägbildachse und der Punkt $A$ links vom Punkt $C$ liegen soll, mit $q = \frac{1}{2}; ω = 45^{\circ}$

Pyramide $A B C D S$

Berechne das Maß des Winkels $S C A$ und die Länge der Strecke $M S$

Zeichne die Pyramide $A C P_{1} B$ für $φ = 35^{\circ}$ in das Schrägbild zu Aufgabe a) ein

Zeige, dass für die Länge der Strecken $A P_{n}$ in Abhängigkeit von $φ$ gilt: $| A P_{n} | (φ) = \frac{9,30}{\sin (φ + {50,83}^{\circ})} cm$

Berechne den zugehörigen Wert von $φ$

Zeige, dass für das Volumen $V$ der Pyramiden $A C P_{n} B$ in Abhängigkeit von $φ$ gilt: $V (φ) = \frac{74,40 \cdot \sin φ}{\sin (φ + {50,83}^{\circ})} {cm}^{3}$

Berechne, um wie viel Prozent das Volumen der Pyramide $A C P_{1} B$ kleiner ist als das Volumen der Pyramide $A B C D S$

In welchem Verhältnis steht das Volumen der Pyramide $A C P_{3} B$ zum Volumen der Pyramide $A B C D S$ ? Begründe