Wahlteil - GTR
🎓 Prüfungsbereich für Niedersachsen
Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen
Startseite
Austausch & Hilfe:
Prüfungen-Discord
- 1
Aufgabe 1A
Gegeben ist die in definierte Funktion mit . Für die erste Ableitungsfunktion von gilt:
Skizzieren Sie den Graphen von in Abbildung 1.
Beschreiben Sie, wie der Graph von aus dem Graphen von erzeugt werden kann. (4 BE)
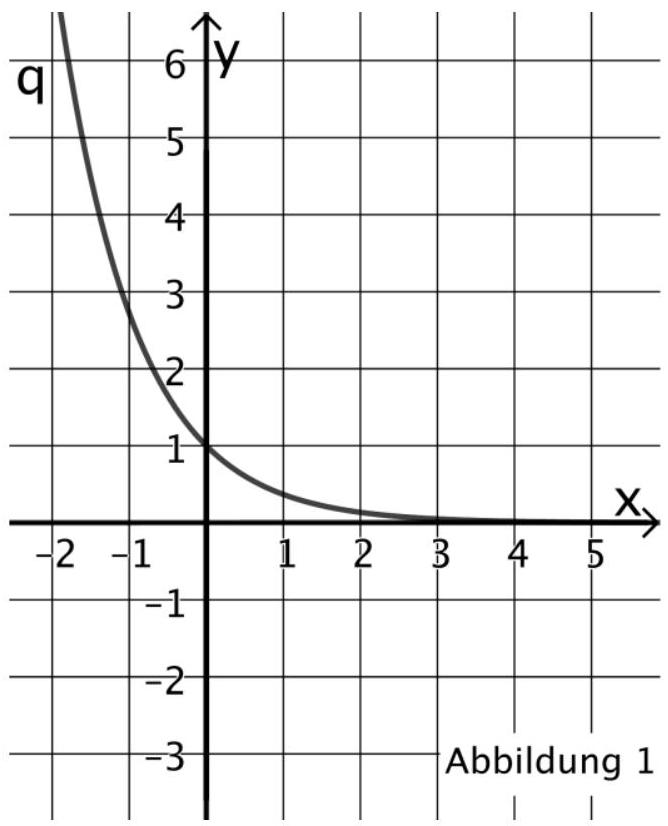
Zeigen Sie, dass mit eine Tangente an den Graphen von an der Stelle 0 ist. (3 BE)
Geben Sie die geometrische Bedeutung der Gleichung an.
Geben Sie den Wert von an. (3 BE)
Gegeben ist die in definierte Funktion mit .
Weiterhin gilt:
Berechnen Sie den Abstand der beiden Extrempunkte des Graphen von . (6 BE)
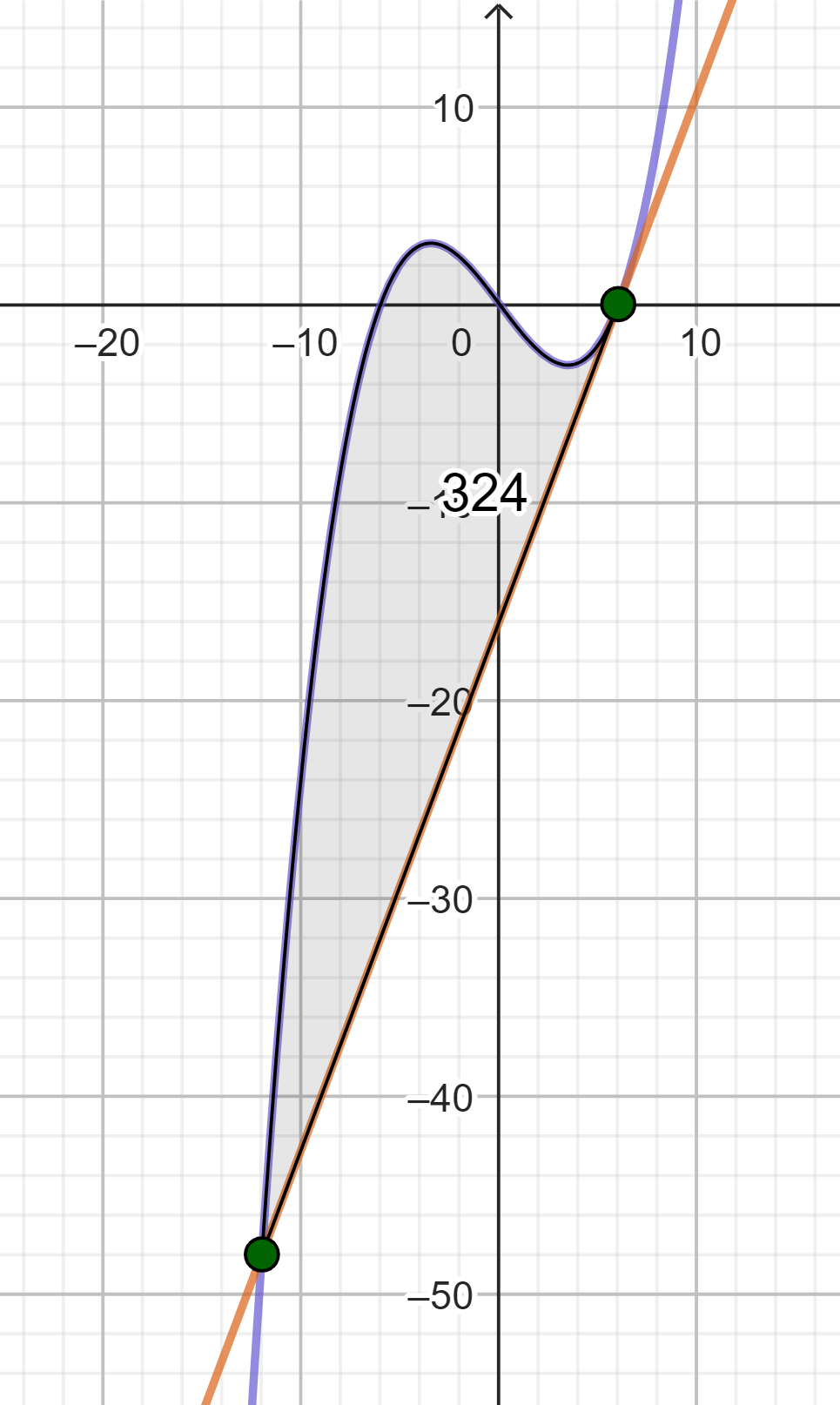
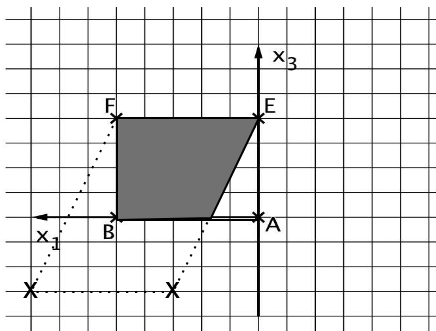
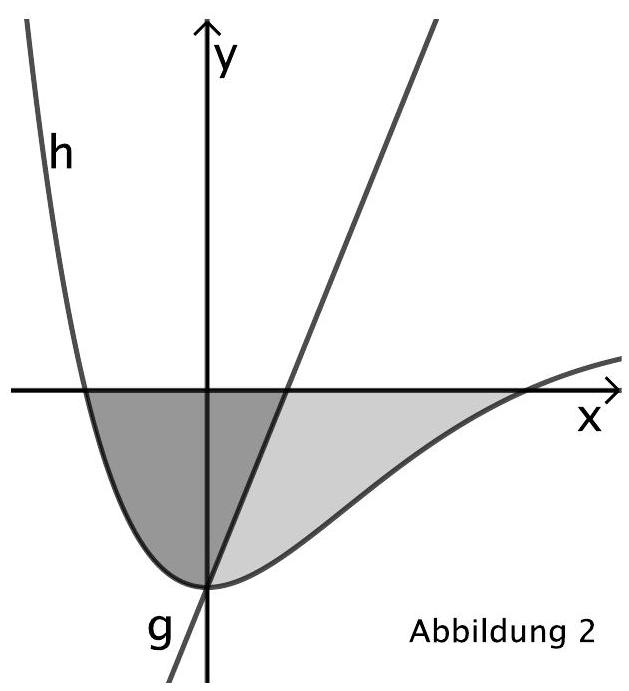
Der Graph von schließt mit der -Achse eine Fläche ein. Die Gerade mit teilt die Fläche in zwei gleich große Teilflächen. Die Abbildung 2 veranschaulicht die Situation.
Bestimmen Sie den Wert für . (6 BE)
Ein Bewässerungskanal wird durch Öffnen einer Schleuse in Betrieb genommen.
Die in definierte Funktion mit
beschreibt für die momentane Durchflussrate des Wassers an einer Messstelle. Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Sekunden und die momentane Durchflussrate in Kubikmetern pro Sekunde . Abbildung 3 zeigt den Graphen von
Bestimmen Sie die momentane Durchflussrate für denjenigen Zeitpunkt, zu dem sie am stärksten abnimmt. (5 BE)
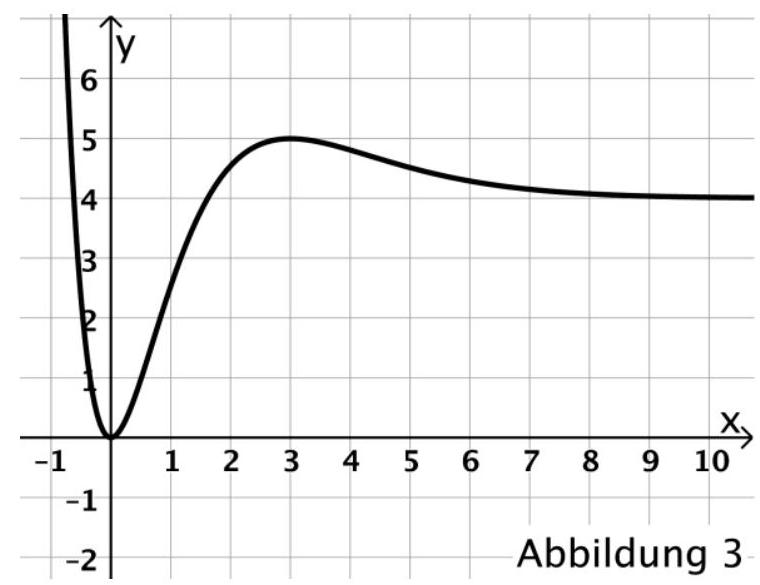
Betrachtet wird der Zeitraum der ersten zehn Sekunden nach Beobachtungsbeginn. Es gilt:
Für den betrachteten Zeitraum beträgt die mittlere Durchflussrate etwa .
Beschreiben Sie die graphische Bedeutung der obigen Aussage und veranschaulichen
Sie geeignete Flächen in der Abbildung 3. (5 BE)
Die Tangente an den Graphen von im Punkt wird mit bezeichnet.
Interpretieren Sie die folgende Aussage im Sachzusammenhang: (3 BE)
Für alle Werte von mit gilt .
- 2
Aufgabe 1B
Die nebenstehende Abbildung zeigt schematisch die Seitenansicht einer Wasserrutschbahn, die aus einem Startbogen, einem Mittelabschnitt und einem
Auslaufbogen zusammengesetzt ist. Die einzelnen Abschnitte werden durch Funktionen beschrieben. Die Funktionen stimmen in den jeweiligen Übergängen in Funktionswerten und Werten der Ableitung überein. Der Auslaufbogen hat in seinem Endpunkt eine waagrechte Tangente. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit. Die -Achse beschreibt die Horizontale.
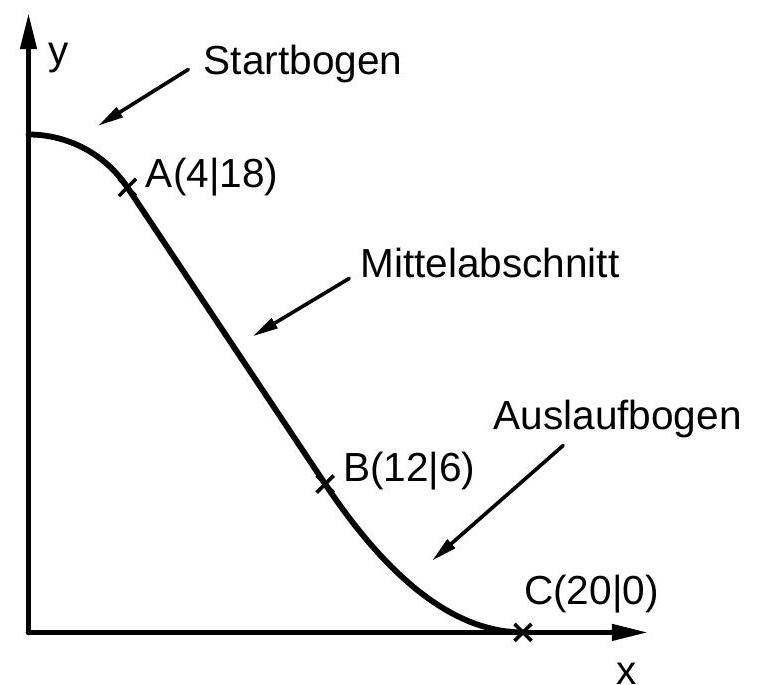
Berechnen Sie eine Gleichung der Gerade, die den Mittelabschnitt beschreibt.
Berechnen Sie die Größe des Winkels dieses Abschnitts der Rutschbahn gegenüber der
Horizontalen. Zur Kontrolle: (6 BE)
Der Auslaufbogen wird mithilfe einer quadratischen Funktion beschrieben.
Bestimmen Sie eine Gleichung von . Zur Kontrolle: (4 BE)
Die Seitenfläche unterhalb der Wasserrutschbahn wird im Bereich verkleidet.
Stellen Sie die entsprechende Fläche in der Abbildung grafisch dar.
Berechnen Sie den Flächeninhalt der Seitenfläche. (6 BE)
Der Startbogen wird mithilfe eines Kreises beschrieben. Er wird durch mehrere Streben gleicher Länge gestützt; diese gehen alle vom selben Punkt aus, der auf der -Achse liegt. Eine der Streben stößt direkt am Übergang zwischen Startbogen und Mittelabschnitt senkrecht auf die Rutschbahn.
Weisen Sie nach, dass der Mittelpunkt des Kreises die Koordinaten hat.
(3 BE)
Berechnen Sie den Radius des Kreises. (3 BE)
Die nebenstehende Abbildung zeigt die vollständige schematische Seitenansicht einer zweiten Wasserrutschbahn. Ihr Verlauf wird mithilfe der in definierten Funktion mit beschrieben. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit. Die -Achse beschreibt die Wasseroberfläche. Die Rutschbahn endet 0,2 Meter oberhalb der Wasseroberfläche.
Geben Sie die Höhe des Startpunkts der Rutschbahn oberhalb der Wasseroberfläche an. Ermitteln Sie die Koordinaten des Endpunktes der Rutschbahn. (4 BE)
Die Rutschbahn weist in mehreren Punkten ihre größte Neigung gegenüber der Horizontalen auf.
Bestimmen Sie diese Neigung in Prozent. (4 BE)
Der Graph von enthält Punkte, in denen die Tangente an den Graphen parallel zur
-Achse verläuft.
Weisen Sie nach, dass diese Punkte alle auf einer Geraden liegen. (5 BE)
- 3
Aufgabe 1C
Gegeben ist die in definierte Funktion mit .
Der Graph von besitzt zwei Extrempunkte. Einer davon hat die -Koordinate .
Der Graph von hat den Wendepunkt
Begründen Sie, dass der Graph von symmetrisch bezüglich seines Wendepunktes ist.
Bestimmen Sie die Koordinaten der Schnittpunkte des Graphen von mit den Koordinatenachsen. (5 BE)
Es gibt Punkte des Graphen von , in denen die Tangente an den Graphen von parallel zur Geraden durch die beiden Extrempunkte des Graphen von ist.
Bestimmen Sie die Koordinaten dieser Punkte. (6 BE)
Bestimmen Sie alle Werte für , sodass der Graph zu genau zwei Nullstellen besitzt. (4 BE)
Die Tangente an den Graphen von im Punkt hat die Gleichung
. Der Graph von und die Tangente schließen eine Fläche ein.
Bestimmen Sie den Inhalt dieser Fläche. (4 BE)
Der Graph von soll in drei Schritten verändert werden. Die drei Schritte sind:
Spiegeln an der -Achse
Verschieben um 6 in positive -Richtung
Verschieben um 14 in positive -Richtung
Geben Sie an, wie viele verschiedene neue Graphen entstehen, nachdem die drei Schritte in allen möglichen Reihenfolgen ausgeführt wurden.
Begründen Sie Ihre Angabe. (5 BE)
Wird der Graph von den drei Schritten in der angegebenen Reihenfolge unterzogen, so entsteht der Graph der in definierten Funktion mit
.
Die Abbildung zeigt den Graphen von .
Die Funktion beschreibt für den Verlauf der Tagesdurchschnittstemperatur an einem bestimmten Ort. Dabei ist die seit einem bestimmten Tag des Kalenderjahres vergangene Zeit in Monaten und die Temperatur in .
Geben Sie die Bedeutung der Wendestelle von hinsichtlich des Verlaufs der Tagesdurchschnittstemperatur an. (3 BE)
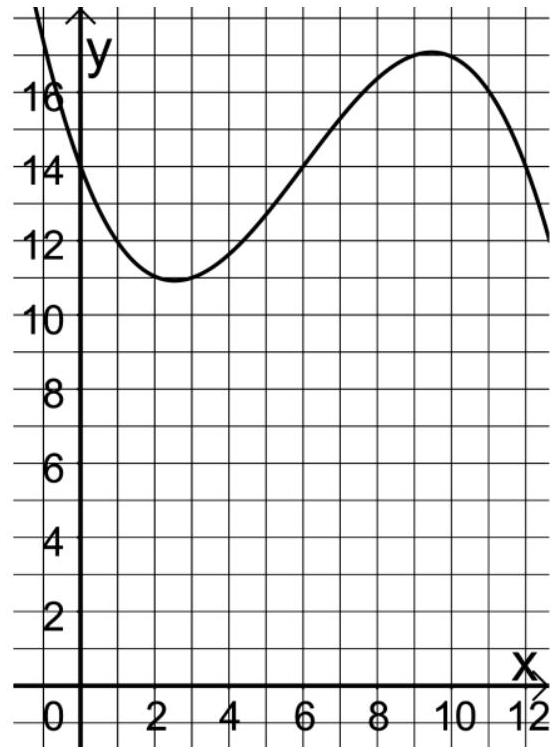
Die folgenden Rechnungen stellen in Verbindung mit der Abbildung die Lösung einer Aufgabe im Sachzusammenhang dar:
oder
Geben Sie eine passende Aufgabenstellung an.
Erläutern Sie den dargestellten Lösungsweg. (5 BE)
Entscheiden Sie, ob die Funktion für geeignet ist, den Verlauf der
Tagesdurchschnittstemperatur an dem betrachteten Ort für ein weiteres Jahr zu beschreiben.
Begründen Sie Ihre Entscheidung. (3 BE)
- 4
Aufgabe 2A
Ein Großhändler bietet Rohkaffee in Säcken zu jeweils an. aller Säcke entsprechen den Qualitätsanforderungen. Die Zufallsgröße beschreibt die Anzahl der Säcke, die den Qualitätsanforderungen entsprechen. Sie ist binomialverteilt.
Der Großhändler liefert Säcke aus.
Bestimmen Sie die zu erwartende Anzahl der Säcke, die den Qualitätsanforderungen entsprechen.
Ermitteln Sie ein -Prognoseintervall für die Anzahl der Säcke, die den Qualitätsanforderungen entsprechen. (5 BE)
Mit dem Term lässt sich die Wahrscheinlichkeit eines
Ereignisses im Sachzusammenhang berechnen.
Geben Sie das Ereignis an. (2 BE)
Ein Kunde prüft die Qualität des Kaffees, bevor er mit dem Großhändler einen Vertrag abschließt. Er untersucht zufällig ausgewählte Säcke daraufhin, ob sie den Qualitätsanforderungen entsprechen.
Wenn dies bei höchstens zwei Säcken nicht der Fall ist, dann wird der Vertrag abgeschlossen.
Wenn genau drei Säcke nicht den Qualitätsanforderungen entsprechen, dann werden in einem zweiten Schritt weitere zufällig ausgewählte Säcke daraufhin untersucht, ob sie den Qualitätsanforderungen entsprechen. Wenn von diesen Säcken höchstens ein Sack nicht den Qualitätsanforderungen entspricht, dann wird der Vertrag abgeschlossen.
Andernfalls kommt der Vertrag nicht zustande.
Ermitteln Sie die Wahrscheinlichkeit dafür, dass der Vertrag abgeschlossen wird. (5 BE)
Weiterhin entsprechen aller Säcke den Qualitätsanforderungen. Jeder Sack, der den
Qualitätsanforderungen nicht entspricht, weist mindestens einen der beiden folgenden Mängel auf:
: „Der Kaffee weist zu viele Verunreinigungen auf.“
: „Der Sack enthält weniger als kg Kaffee.“
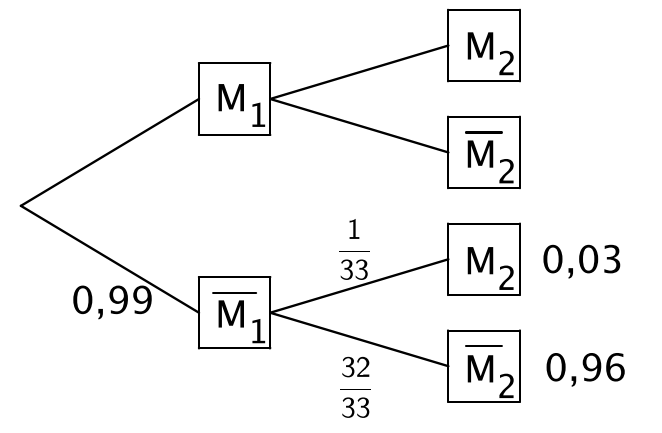
Ein Sack wird zufällig ausgewählt. Die Wahrscheinlichkeit dafür, dass dieser Sack den Mangel aufweist, beträgt .
Ergänzen Sie die Wahrscheinlichkeiten in den Feldern in der unteren Hälfte des Baumdiagramms. (4 BE)
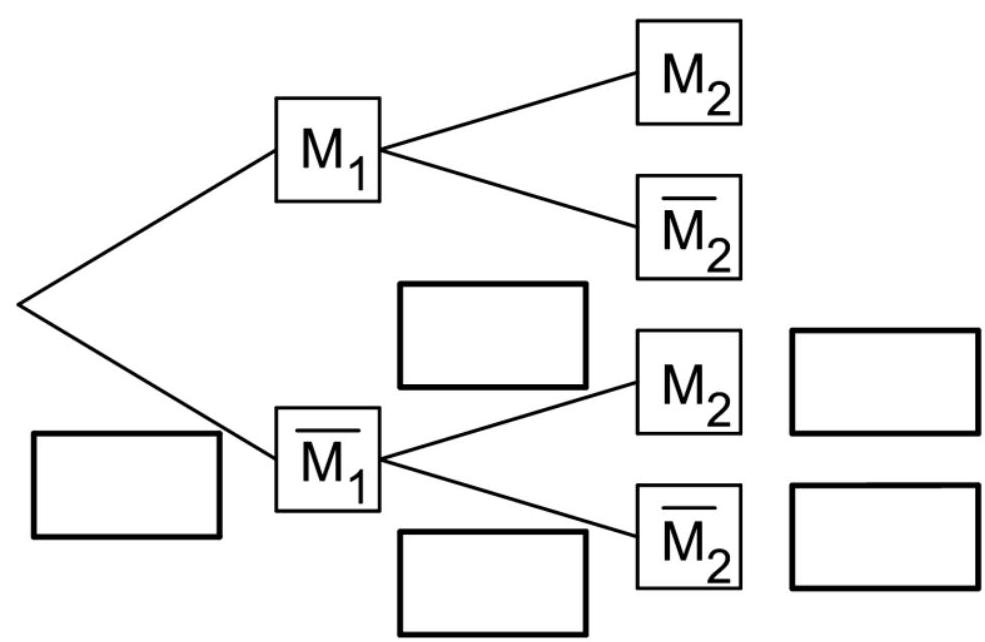
Das Auftreten der beiden Mängel ist stochastisch unabhängig.
Erläutern Sie im Sachkontext die Auswirkungen dieser Eigenschaft auf die Wahrscheinlichkeiten in der oberen Hälfte des Baumdiagramms. (4 BE)
- 5
Aufgabe 2B
Die Abbildung zeigt das Netz eines Würfels.
Der Würfel wird -mal geworfen.
Die Zufallsgröße gibt an, wie oft die Zahl erzielt wird.
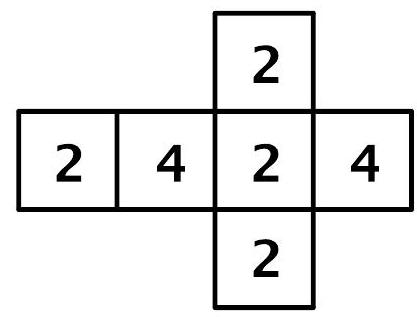
Abbildung 1
Begründen Sie, dass binomialverteilt mit dem Parameter ist. (3 BE)
Ermitteln Sie die Wahrscheinlichkeit dafür, dass die Zahl häufiger erzielt wird als die Zahl „“. (3 BE)
Bestimmen Sie das kleinstmögliche zum Erwartungswert symmetrische Intervall, in dem die Anzahl der Würfe, in denen eine erzielt wird, mit einer Wahrscheinlichkeit von mindestens liegt. (3 BE)
Geben Sie im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem Term berechnet werden kann. (2 BE)
Bei einem Spiel mit diesem Würfel werfen zwei Personen abwechselnd. Das Spiel ist beendet, wenn eine Person eine andere Zahl würfelt als die andere Person direkt vorher.
Es gewinnt die Person, die in ihrem letzten Wurf die größere Zahl hat.
Eine der beiden Personen beginnt das Spiel.
Berechnen Sie die Wahrscheinlichkeit dafür, dass diese Person verliert und der Würfel insgesamt höchstens viermal geworfen wird. (5 BE)
Die Abbildung zeigt das Netz eines weiteren Würfels.
Der Würfel wird -mal geworfen.
Bei den ersten Würfen wird -mal die Zahl erzielt.
Ermitteln Sie die Wahrscheinlichkeit dafür, dass bei höchstens der insgesamt Würfe die Zahl erzielt wird. (4 BE)
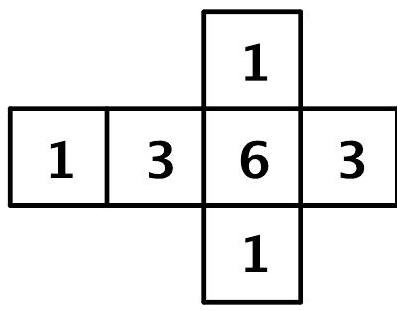
Abbildung 2
- 6
Aufgabe 2C
In einem Land arbeiten der Lehrkräfte an einem Gymnasium. der Lehrkräfte sind weiblich und arbeiten an einem Gymnasium. Insgesamt sind der Lehrkräfte weiblich.
Stellen Sie den Sachzusammenhang in einer vollständig ausgefüllten Vierfeldertafel dar. (4 BE)
Eine zufällig ausgewählte Lehrkraft ist weiblich.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass sie an einem Gymnasium arbeitet. (2 BE)
Lehrkräfte werden zufällig ausgewählt.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass unter diesen Lehrkräften die Anzahl derer, die nicht am Gymnasium arbeiten, mindestens viermal so groß ist, wie die Anzahl derer, die am Gymnasium arbeiten. (3 BE)
Geben Sie die Bedeutung des Terms im Sachzusammenhang an: (3 BE)
Im Folgenden wird ein Spiel betrachtet. In einem Behälter befinden sich vier weiße und fünf schwarze Kugeln. Der Spieler bezahlt zunächst einen Einsatz von Euro. Dieser Betrag wird neben dem Behälter ausgelegt. Anschließend muss der Spieler aus dem Behälter zweimal nacheinander eine Kugel zufällig ziehen und wieder zurücklegen. Nach jedem der beiden Züge wird der ausliegende Betrag vom Spielleiter verdoppelt, wenn eine weiße Kugel gezogen wird, und sonst halbiert. Nach dem Spiel erhält der Spieler den dann ausliegenden Betrag.
Der Term gibt den Erwartungswert für den Betrag in Euro an, den der Spieler nach dem Spiel erhält.
Interpretieren Sie den zweiten der drei Summanden im Sachzusammenhang. (4 BE)
In einem weiteren Behälter befinden sich ebenfalls weiße und schwarze Kugeln.
Ermitteln Sie, wie das Verhältnis der Anzahlen der weißen und schwarzen Kugeln in diesem Behälter sein muss, damit das Spiel fair ist. (4 BE)
- 7
Aufgabe 3A
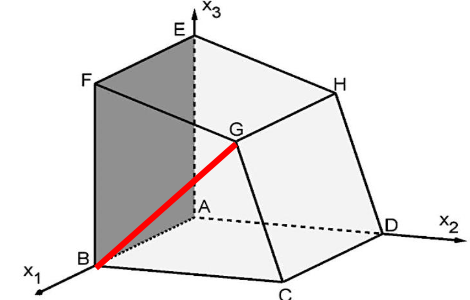
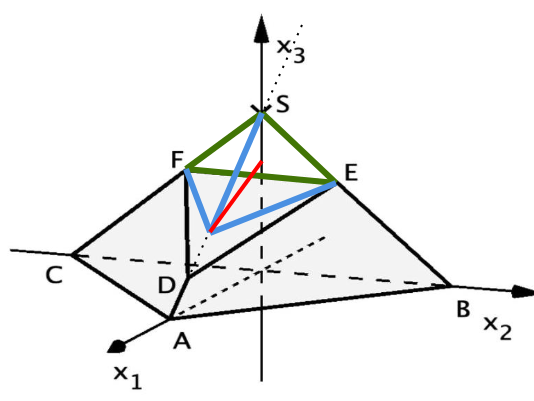
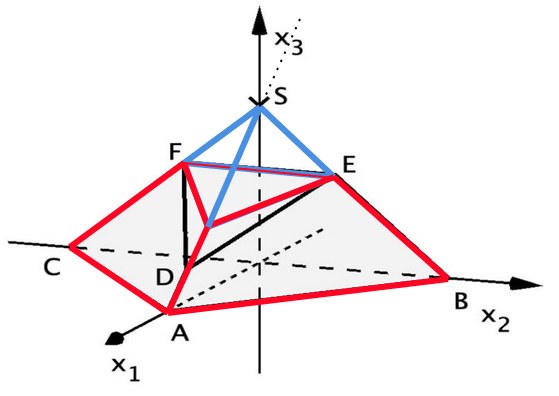
Ein Anbau eines Gebäudes wird durch das abgebildete Prisma mit den Eckpunkten , und beschrieben.
Das Viereck stellt das Glasdach dar, das
Viereck eine geschlossene Wand. Die anderen Seiten des Anbaus bestehen vollständig aus Glas.
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
Die -Ebene beschreibt den Untergrund, auf dem der Anbau steht.
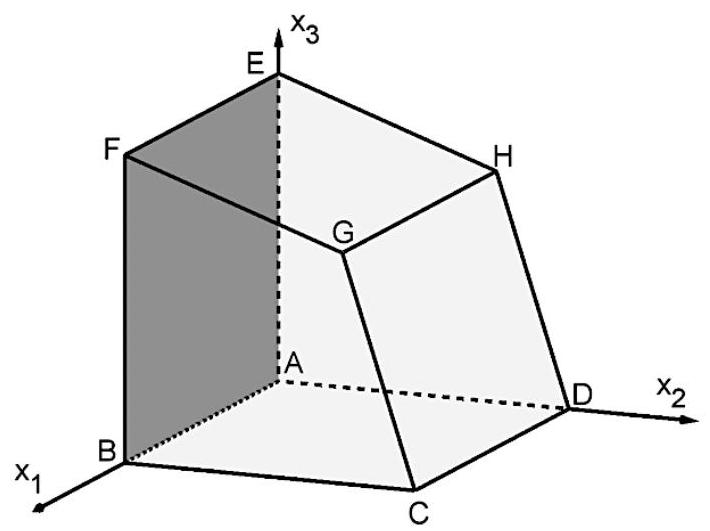
Begründen Sie, dass das Viereck ein Drachenviereck ist. (3 BE)
Bestimmen Sie die Größe des Winkels, den die Kanten und einschließen. (3 BE)
Die Punkte und liegen in der Ebene .
Zeigen Sie, dass ein Spannvektor von ist. (3 BE)
Begründen Sie, dass das Viereck das Prisma in zwei zueinander symmetrische Teilkörper teilt. (3 BE)
Auf dem Glasdach kann ein Rollo herabgelassen werden. Dabei bewegt sich das Rollo innerhalb einer Minute von der oberen Kante des Dachs, die durch dargestellt wird, bis zur unteren Kante des Dachs.
Bestimmen Sie die mittlere Geschwindigkeit, mit der das Rollo herabgelassen wird, in Zentimeter pro Sekunde. (3 BE)
Zu einem bestimmten Zeitpunkt kann das auf den Anbau treffende Sonnenlicht durch parallele Geraden mit dem Richtungsvektor beschrieben werden.
Das vollständig herabgelassene Rollo erzeugt auf der geschlossenen Wand einen Schatten. Dieser soll in der -Ebene grafisch dargestellt werden. Die folgende Rechnung stellt einen wesentlichen Schritt zur Lösung dieser Aufgabe dar:
Beschreiben Sie die Bedeutung dieses Lösungsschritts und zeichnen Sie den Schatten in die folgende Abbildung ein. (5 BE)
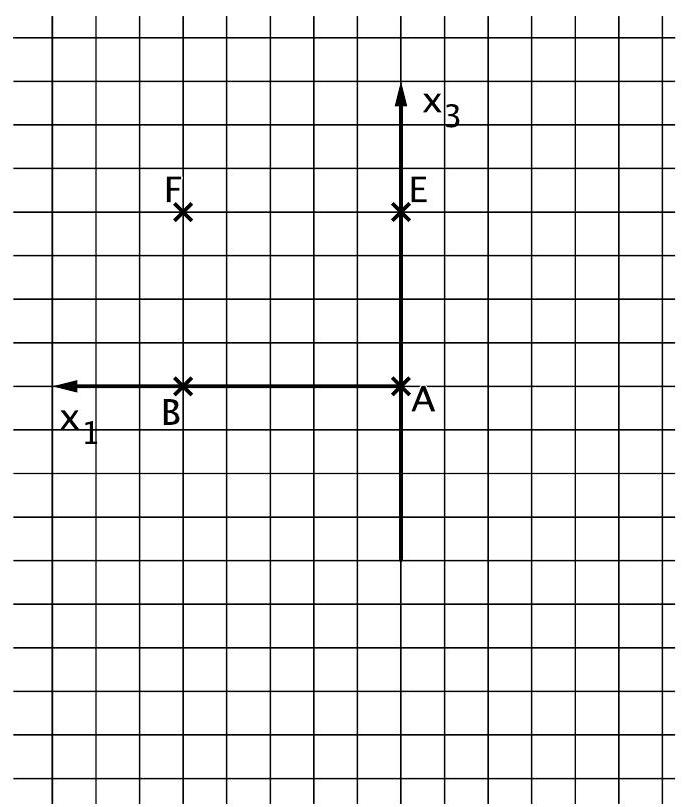
- 8
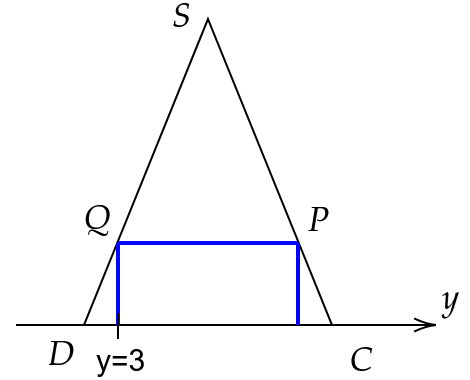
Aufgabe 3B
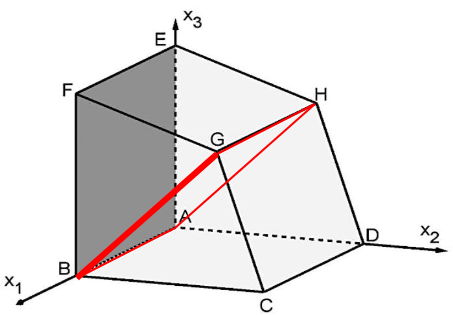
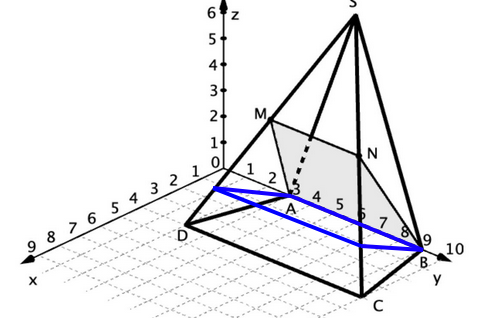
Die Abbildung zeigt die Pyramide mit
und sowie der Spitze im Punkt .
bezeichnet den Mittelpunkt der Kante und bezeichnet den Mittelpunkt der Kante .
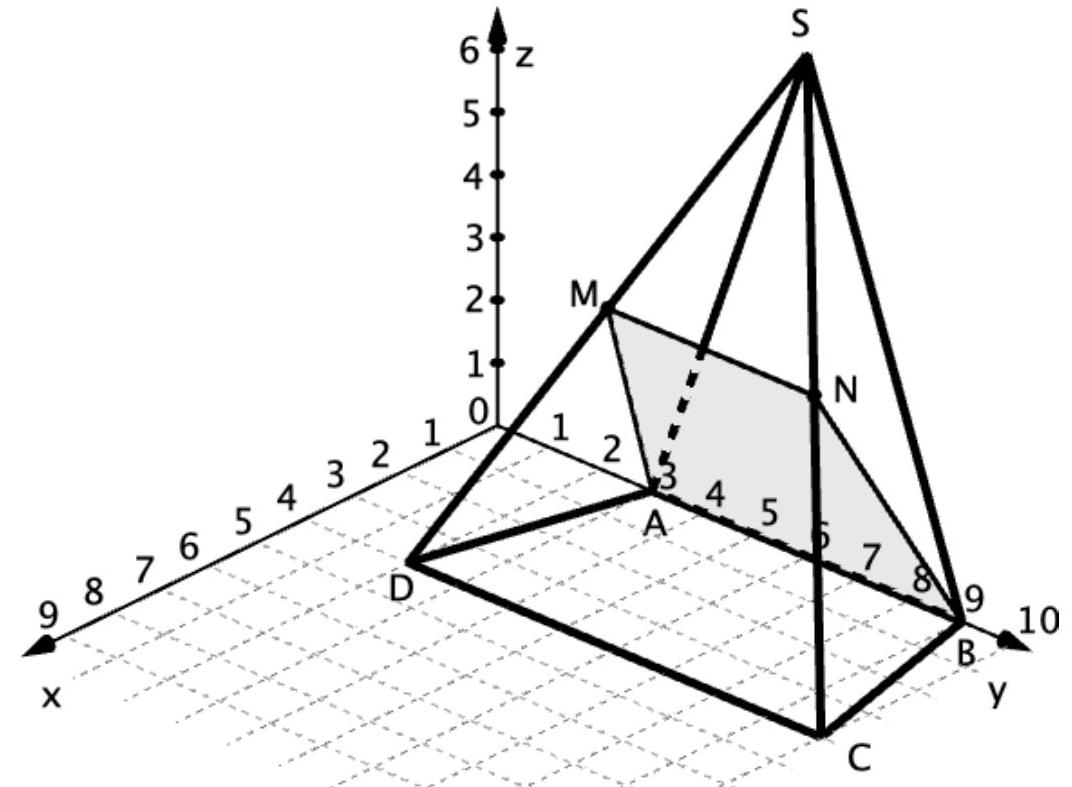
Begründen Sie, dass das Dreieck gleichschenklig ist.
Bestimmen Sie eine Gleichung für die Gerade, auf der die Symmetrieachse des Dreiecks DCS liegt. (6 BE)
Berechnen Sie den von den Kanten und eingeschlossenen Winkel. (4 BE)
Die Punkte und sind die Eckpunkte eines Trapezes.
Betrachtet wird jetzt ein beliebiger Punkt auf der Kante sowie ein beliebiger Punkt auf der Kante .
Begründen Sie, dass die Punkte und die folgenden Koordinaten haben: (5 BE)
mit
mit
Untersuchen Sie, ob es einen Punkt sowie einen Punkt gibt, sodass das Viereck ein Rechteck ist. (5 BE)
- 9
Aufgabe 3C
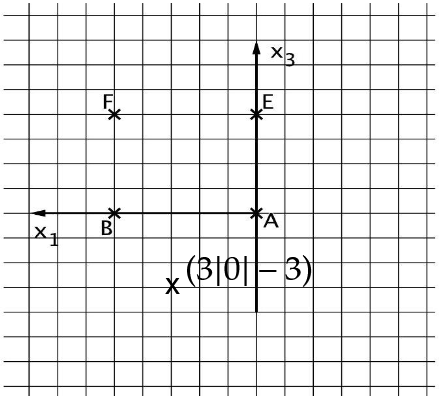
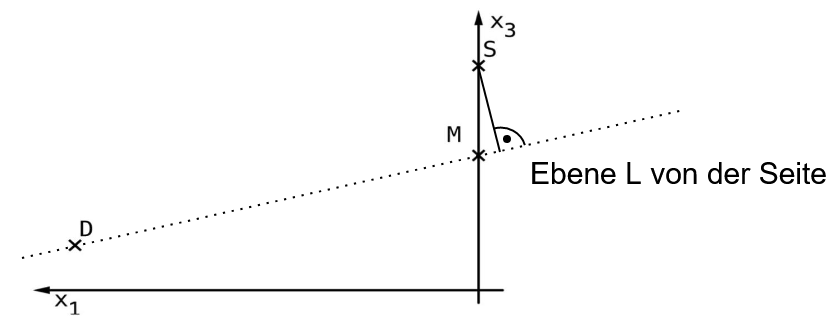
Die Abbildung zeigt den Körper mit und . Das Dreieck wird als Grundfläche und das Dreieck als Deckfläche des Körpers bezeichnet. Die Deckfläche liegt in der Ebene .
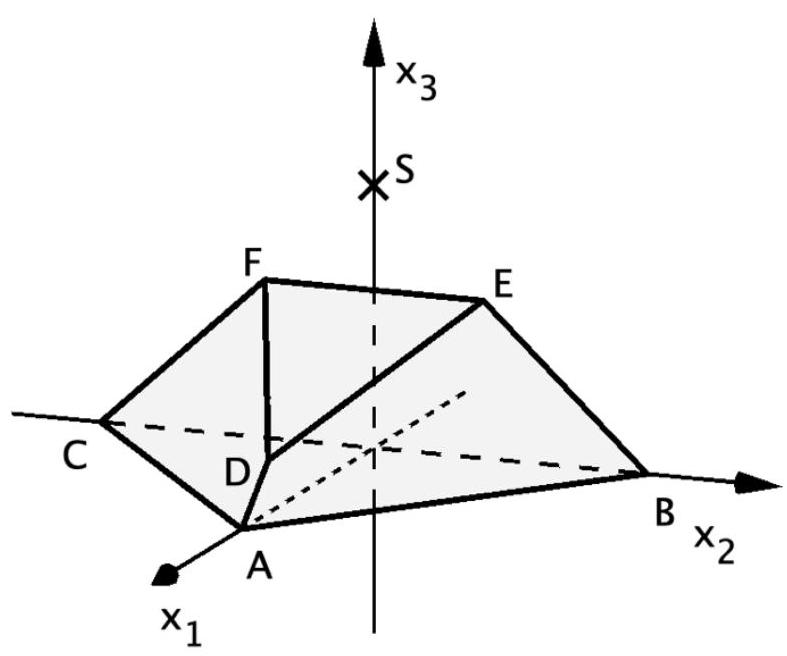
Zeigen Sie, dass das Dreieck gleichschenklig ist. Berechnen Sie den Innenwinkel des Dreiecks im Eckpunkt .
Begründen Sie, dass die Kante parallel zur Grundfläche liegt. (7 BE)
Der Körper kann zu einer Pyramide mit der Grundfläche und der Spitze ergänzt werden, wobei und auf den Kanten der Pyramide liegen.
Begründen Sie, dass in der -Ebene liegt. (5 BE)
Berechnen Sie die Koordinaten von . [Zur Kontrolle: ]
ist auch Spitze einer Pyramide mit der Grundfläche . Die nebenstehende Abbildung zeigt in der -Ebene die Punkte und sowie den Mittelpunkt der Kante .
Begründen Sie, dass der Abstand von zur Ebene kleiner als ist, und veranschaulichen Sie Ihre Begründung durch geeignete Eintragungen in der untenstehenden Abbildung. (4 BE)

Für besitzen die Punkte der Strecke die -Koordinate .
ist der Flächeninhalt des Dreiecks EFS.
Begründen Sie, dass das Volumen der Pyramide mit dem Term berechnet werden kann.
Beschreiben Sie ein Vorgehen zur Berechnung des Volumens des Körpers .
(4 BE)