Spurpunkte einer Geraden

Spurpunkte sind die Schnittpunkte einer Geraden $g : \vec{X} = \vec{A} + r \cdot \vec{u}$ mit den Koordinatenebenen des Koordinatensystems.

Mithilfe der Spurpunkte kann eine Gerade im Koordinatensystem gezeichnet werden.

Anzahl der Spurpunkte

$1$ Spurpunkt $\Rightarrow$ Gerade ist parallel zu einer Koordinatenachse (und liegt nicht in einer der drei Koordinatenebenen)
$2$ Spurpunkte $\Rightarrow$ Gerade ist parallel zu einer Koordinatenebene (und liegt nicht in dieser Koordinatenebene)
$3$ Spurpunkte $\Rightarrow$ Gerade ist nicht parallel zu einer der drei Koordinatenebenen
unendlich viele Spurpunkte $\Rightarrow$ Gerade liegt in einer der Koordinatenebenen oder liegt auf einer der Koordinatenachsen

Sonderfälle

Gerade schneidet eine Koordinatenachse $\Rightarrow$ $2$ Spurpunkte fallen zusammen und haben gleiche Koordinaten
Gerade geht durch den Koordinatenursprung $\Rightarrow$ alle 3 Spurpunkte fallen zusammen

Wie werden die Spurpunkte berechnet?

Spurpunkt der Geraden $g$ in der $x_{1} x_{2}$ -Ebene $S_{12}$ $\Rightarrow$ man setzt $x_{3} = 0$

Spurpunkt der Geraden $g$ in der $x_{1} x_{3}$ -Ebene $S_{13}$ $\Rightarrow$ man setzt $x_{2} = 0$

Spurpunkt der Geraden $g$ in der $x_{2} x_{3}$ -Ebene $S_{23}$ $\Rightarrow$ man setzt $x_{1} = 0$

Die jeweils aufgestellte Gleichung wird nach dem Parameter $r$ aufgelöst.

Der für $r$ berechnete Wert wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes zu erhalten.

VorsichtEs gibt nicht immer eine eindeutige Lösung der aufgestellten Gleichung!

Hat die aufgestellte Gleichung keine Lösung, dann gibt es keinen Spurpunkt in dieser Koordinatenebene.
Hat die Gleichung dagegen unendlich viele Lösungen, dann liegen in dieser Koordinatenebene unendlich viele Spurpunkte.

Beispiel für die Berechnung der Spurpunkte

Gegeben ist die Gerade $g : \vec{X} = (\begin{array}{c} 2 \\ 5 \\ 6 \end{array}) + r \cdot (\begin{array}{c} 2 \\ 0 \\ 3 \end{array})$ . Bestimme mögliche Spurpunkte von $g$ .

Berechnung des Spurpunktes $S_{12}$ in der $x_{1} x_{2}$ -Ebene

Um den Spurpunkt in der $x_{1} x_{2}$ -Ebene zu berechnen, setzt man $x_{3} = 0$ in der Geradengleichung und berechnet den Parameter $r$ :

$x_{3}$	$=$	$6 + 3 \cdot r$
	↓	Setze $x_{3} = 0$ .
$0$	$=$	$6 + 3 \cdot r$	$- 6$
	↓	Löse nach $r$ auf.
$- 6$	$=$	$3 \cdot r$	$: 3$
$- 2$	$=$	$r$

$r = - 2$ wird in die Geradengleichung eingesetzt, um den Spurpunkt in der $x_{1} x_{2}$ -Ebene zu berechnen:

${\vec{X}}_{S_{12}}$	$=$	$(\begin{array}{c} 2 \\ 5 \\ 6 \end{array}) + r \cdot (\begin{array}{c} 2 \\ 0 \\ 3 \end{array})$
	↓	Setze $r = - 2$ ein.
	$=$	$(\begin{array}{c} 2 \\ 5 \\ 6 \end{array}) + (- 2) \cdot (\begin{array}{c} 2 \\ 0 \\ 3 \end{array})$
	$=$	$(\begin{array}{c} 2 - 4 \\ 5 - 0 \\ 6 - 6 \end{array})$
	↓	Vereinfache.
	$=$	$(\begin{array}{c} - 2 \\ 5 \\ 0 \end{array})$

Der Spurpunkt in der $x_{1} x_{2}$ -Ebene hat die Koordinaten $S_{12} (- 2 | 5 | 0)$ .

Berechnung des Spurpunktes $S_{13}$ in der $x_{1} x_{3}$ -Ebene

Für die Berechnung des Spurpunktes in der $x_{1} x_{3}$ -Ebene setzt man $x_{2} = 0$ in der Geradengleichung und berechnet den Parameter $r$ .

$x_{2}$	$=$	$5 + r \cdot 0$
	↓	Setze $x_{2} = 0$ .
$0$	$=$	$5 + r \cdot 0$

Die erhaltene Gleichung $0 = 5 + r \cdot 0$ ist für kein $r$ erfüllbar (falsche Aussage).

Somit gibt es keinen Spurpunkt in der $x_{1} x_{3}$ -Ebene.

Die Gerade $g$ verläuft parallel zur $x_{1} x_{3}$ -Ebene.

Graphische Veranschaulichung

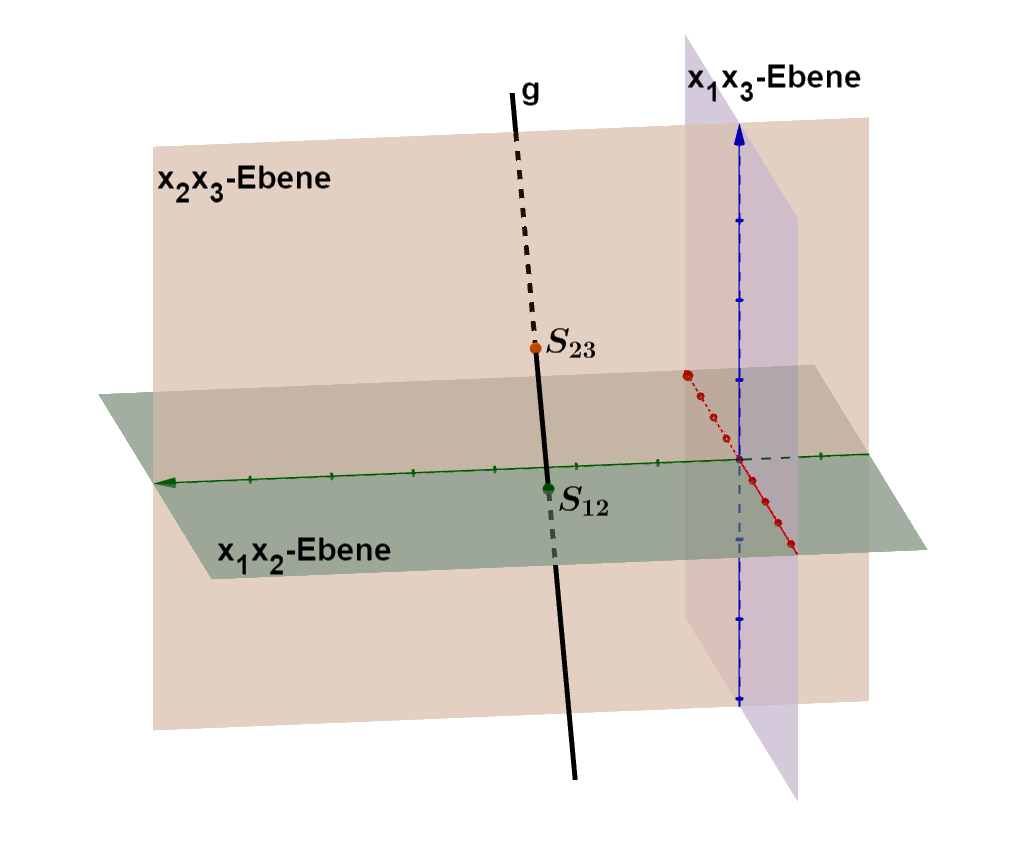
Allgemeine Vorgehensweise für die Berechnung der Spurpunkte

Der Spurpunkt $S_{12}$ in der $x_{1} x_{2}$ -Ebene soll berechnet werden. In der $x_{1} x_{2}$ -Ebene gilt immer $x_{3} = 0$ .

1. Man setzt die $x_{3}$ -Koordinate eines Punktes der Geraden $g : \vec{X} = \vec{A} + r \cdot \vec{u}$ gleich null und berechnet den Wert für den Parameter $r$ :

$x_{3}$	$=$	$a_{3} + r \cdot u_{3}$
	↓	Setze $x_{3} = 0$ .
$0$	$=$	$a_{3} + r \cdot u_{3}$	$- a_{3}$
	↓	Löse nach $r$ auf.
$- a_{3}$	$=$	$r \cdot u_{3}$	$: u_{3}$
$r$	$=$	$- \frac{a_{3}}{u_{3}}$

Achtung: Eine Lösung ergibt sich nur für $u_{3} \neq 0$ , andernfalls ist die Gerade $g$ parallel zur $x_{1} x_{2}$ -Ebene oder die Gerade $g$ liegt in der $x_{1} x_{2}$ -Ebene.

2. Der berechnete Wert für $r = - \frac{a_{3}}{u_{3}}$ wird in die Geradengleichung eingesetzt, um die Koordinaten des Spurpunktes zu berechnen $\Rightarrow {\vec{X}}_{S_{12}} = \vec{A} - \frac{a_{3}}{u_{3}} \cdot \vec{u}$ .

Für die anderen beiden Spurpunkte $S_{13}$ und $S_{23}$ geht man analog vor.

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org