Inkreis eines Dreiecks
Der Inkreis eines Dreiecks, ist der Kreis, der alle Seiten von innen genau einmal berührt. Alle Seiten sind also Tangenten des Inkreises. Sein Mittelpunkt ist der Schnittpunkt der Winkelhalbierenden.
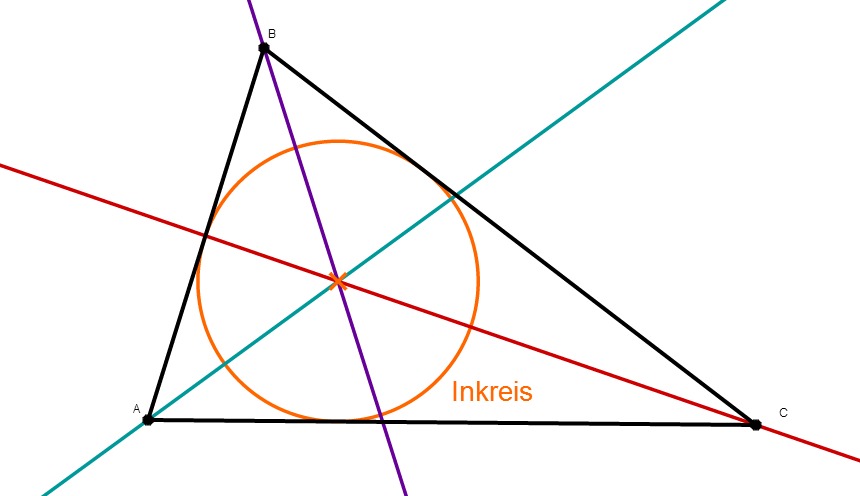
Konstruktion
Konstruiere zwei Winkelhalbierende im Dreieck.
Fälle ein Lot auf einer Dreiecksseite durch den Schnittpunkt der Winkelhalbierende.
Zeichne den Inkreis, dessen Mittelpunkt der Schnittpunkt der Winkelhalbierende ist und der durch den Lotfußpunkt geht.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.
Anmerkung:
Bei der Bestimmung des Inkreismittelpunktes reicht es aus, wenn man nur zwei Winkelhalbierende konstruiert, da die Dritte auch durch den Schnittpunkt geht.
Der Inkreis ist der größte Kreis der im Inneren eines Dreiecks liegt.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:



