Nachtermin Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Nebenstehende Skizze zeigt das rechtwinklige Dreieck $A B C$ mit der Hypotenuse $[A C]$ . $M$ ist der Mittelpunkt der Strecke $[A B]$ .
Punkte $P_{n}$ liegen auf der Strecke $[A C]$ mit $A P_{n} = x cm (x \in ℝ; x \in] 0; 10,86 [)$ .
Es gilt: $A B = 9 cm; ∡ B A C = 34 °; ∡ B M P_{1} = 70 ° .$
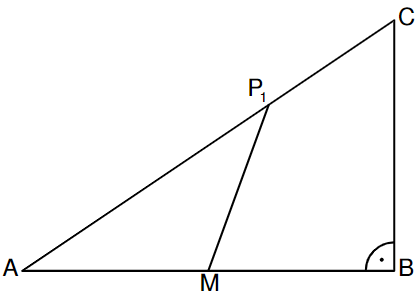
Berechnen Sie die Längen der Strecken $[A C_{1}]$ und $[A P_{1}]$ .
Runden Sie auf zwei Stellen nach dem Komma.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie (Kosinus), Sinussatz, Nebenwinkel, Innenwinkelsumme im Dreieck
Teilaufgabe a
Länge der Strecke $[A C]$ :
Das Dreieck ABC ist rechtwinklig: daher können wir den Kosinus verwenden:
$\cos (α) = \frac{Ankathete}{Hypotenuse}$
$\cos (34 °) = \frac{9 cm}{A C}$
$A C = \frac{9 cm}{\cos (34 °)} \approx 10,86 cm$
Länge der Strecke $A P_{1}$ :
$∡ P_{1} M A = 180 ° - 70 ° = 110 °$ (Nebenwinkel).
$∡ M P_{1} A = 180 ° - 110 ° - 34 ° = 36 °$ (Innenwinkelsumme im Dreieck)
Sinussatz:
$\frac{a}{\sin (α)} = \frac{b}{\sin (β)}$
$\frac{A M}{\sin (36 °)} = \frac{A P_{1}}{\sin (110 °)}$
$A P_{1} = \frac{A M \cdot \sin (110 °)}{\sin (36 °)}$
$A P_{1} = \frac{4,5 cm \cdot \sin (110 °)}{\sin (36 °)} \approx 7,19 cm$

Begründen Sie, weshalb für alle Punkte $P_{n}$ gilt: $∡ B M P_{n} + ∡ M P_{n} C = 214 °$ .

Teilaufgabe b
$∡ B M P_{n} + ∡ M P_{n} C = 214 ° :$
$∡ M P_{1} C = 180 ° - 36 ° = 144 °$ (Nebenwinkel)
$∡ B M P_{n} + ∡ M P_{n} C = 70 ° + 144 ° = 214 °$
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Parabel $p$ mit dem Scheitelpunkt $S (2 | - 3)$ hat eine Gleichung der Form $y = 0,4 x^{2} + b x + c$ mit $(𝔾 = ℝ \times ℝ und b, c \in ℝ)$ . Die Gerade $g$ hat die Gleichung $y = - 0,3 x + 4$ $(𝔾 = ℝ \times ℝ) .$
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
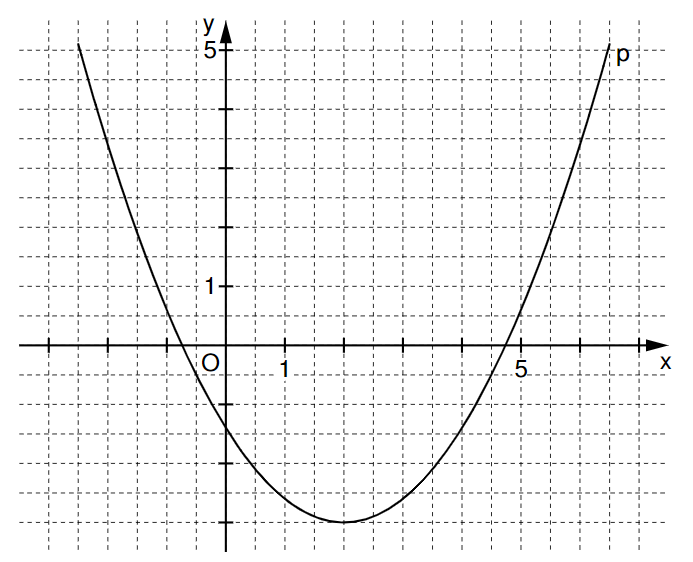
Zeigen Sie durch Rechnung, dass die Parabel $p$ die Gleichung
$y = 0,4 x^{2} - 1,6 x - 1,4$ hat und zeichnen Sie die Gerade $g$ für $x \in [- 3; 7]$ in das Koordinatensystem zur Aufgabenstellung ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Quadrat, Mitternachtsformel
Teilaufgabe a
Die Parabel hat die Gleichung $y = 0,4 x^{2} - 1,6 x - 1,4$
Stelle zunächst mithilfe des Scheitelpunktes $S (2 | - 3)$ die Scheitelpunktform auf.
allgemein:
$y = a {(x - d)}^{2} + e$
Da die Parabel die Form $a {(x - d)}^{2} + e$ haben soll, können wir die fehlenden Variablen einsetzen: $a = 0,4, d = 2$ und $e = - 3$ .
$y$ $=$ $0,4 {(x - 2)}^{2} - 3$
↓
Binomische Formel anwenden.
$=$ $0,4 (x^{2} - 4 x + 4) - 3$
↓
Klammer ausmultiplizieren.
$=$ $0,4 x^{2} - 1,6 x + 1,6 - 3$
↓
Zusammenfassen.
$=$ $0,4 x^{2} - 1,6 x - 1,4$
Einzeichnen der Geraden $g : y = - 0,3 x + 4$ :
Da die lineare Funktion einen y-Achsenabschnitt $b = 4$ hat, haben wir den Startpunkt $A$ (siehe Zeichnung unten) und eine Steigung $m = - 0,3 = - \frac{3}{10}$
(Wir gehen $10$ Einheiten nach rechts und $3$ nach unten.)

Punkte $A_{n} (x | 0,4 x^{2} - 1,6 x - 1,4)$ auf der Parabel $p$ und Punkte $C_{n} (x | - 0,3 x + 4)$ auf der Geraden $g$ haben dieselbe Abszisse $x$ und sind für $x \in] - 2,39; 5,64 [$ Eckpunkte von Rauten $A_{n} B_{n} C_{n} D_{n}$ . Dabei gilt: $B_{n} D_{n} = 4 LE$ .
Zeichnen Sie die Raute $A_{1} B_{1} C_{1} D_{1}$ für $x = 2$ in das Koordinatensystem zur Aufgabenstellung ein.

Teilaufgabe b
Einzeichnen einer Raute für $x = 2$ in das Koordinatensystem:
Einsetzen von $x = 2$ in die Koordinaten $A_{n} (x | 0,4 x^{2} - 1,6 x - 1,4)$ und $C_{n} (x | - 0,3 x + 4)$ .
$y (2)$ $=$ $0,4 \cdot 2^{2} - 1,6 \cdot 2 - 1,4$
$=$ $0,4 \cdot 4 - 3,2 - 1,4$
$=$ $1,6 - 3,2 - 1,4$
$=$ $- 3$
$y (2)$ $=$ $- 0,3 \cdot 2 + 4$
$=$ $- 0,6 + 4$
$=$ $3,4$
Damit haben wir die Koordinaten $A (2 | 3)$ und $C (2 | 3,4)$ .
$A$ und $C$ einzeichnen und verbinden.
Das Viereck $A B C D$ ist ein Drachenviereck, also sind [ $A_{n} C_{n}$ ] und [ $B_{n} D_{n}$ ] Symmetrieachsen.
Mittelsenkrechte zu $[A C]$ .
Da wir wissen, dass $B_{n} D_{n} = 4 LE$ ist, können wir $D M = M B = 2 LE$ abmessen.

Berechnen Sie den Flächeninhalt $A$ der Rauten $A_{n} B_{n} C_{n} D_{n}$ in Abhängigkeit von $x$ und begründen Sie sodann, weshalb es unter den Rauten $A_{n} B_{n} C_{n} D_{n}$ keine Raute mit einem Flächeninhalt von $15 FE$ geben kann.
$[Zwischenergebnis : A_{n} C_{n} (x) = (- 0,4 x^{2} + 1,3 x + 5,4) LE]$

Teilaufgabe c
Flächeninhalt $A$ der Raute $A_{n} B_{n} C_{n} D_{2}$ :
allgemein: $A_{Drache} = \frac{e \cdot f}{2}$
Wir kennen die Diagonale $e = D M = 4 LE$ . Die Diagonale $f$ ermitteln wir, indem wir die y-Koordinate von $A_{n}$ von $C_{n}$ abziehen:
$[A_{n} C_{n}]$ $=$ $(- 0,3 x + 4 - (0,4 x^{2} - 1,6 x - 1,4)) LE$
↓
Klammer auflösen.
$=$ $(- 0,3 x + 4 - 0,4 x^{2} + 1,6 x + 1,4) LE$
↓
Zusammenfassen.
$=$ $(- 0,4 x^{2} + 1,3 x + 5,4) LE$
In die Formel einsetzen:
$A_{Drache}$ $=$ $\frac{e \cdot f}{2}$
↓
Einsetzen.
$=$ $\frac{(4 \cdot (- 0,4 x^{2} + 1,3 x + 5,4)) LE}{2}$
↓
Kürzen.
$=$ $(2 \cdot (- 0,4 x^{2} + 1,3 x + 5,4)) LE$
↓
Klammer ausrechnen.
$=$ $(- 0,8 x^{2} + 2,6 x + 10,8) LE$
Die Flächenformel ist eine Parabel, gesucht ist der Extrempunkt (Scheitelpunkt):
Scheitelpunkt mithilfe der Formel: $S (\frac{- b}{2 \cdot a} | c - \frac{b^{2}}{4 \cdot a})$
In diesem Fall ist nur $y$ interessant.
Aus der Gleichung $y = - 0,8 x^{2} + 2,6 x + 10,8$ ist zu schließen, dass $a = - 0,8$ , $b = 2,6$ und $c = 10,8$ .
(allgemein: $y = a x^{2} + b x + c$ ⁣)
$y oder A_{\max}$ $=$ $c - \frac{b^{2}}{4 \cdot a}$
$=$ $10,8 - \frac{{2,6}^{2}}{4 \cdot (- 0,8)}$
$=$ $10,6 - \frac{169}{80}$
$\approx$ $12,91 FE$
$<$ $15 FE$
Folglich gibt es keine Raute mit einem Flächeninhalt von $15 FE$ .

Unter den Rauten $A_{n} B_{n} C_{n} D_{n}$ gibt es die Quadrate $A_{2} B_{2} C_{2} D_{2}$ und $A_{3} B_{3} C_{3} D_{3}$ .
Bestimmen Sie rechnerisch die $x$ -Koordinaten der Punkte $B_{2}$ und $B_{3}$ .

Teilaufgabe d
x-Koordinaten der Quadrate $A_{2} B_{2} C_{2} D_{2}$ und $A_{3} B_{3} C_{3} D_{3}$ :
Wenn die Raute $A_{n} B_{n} C_{n} D_{n}$ ein Quadrat sein soll, dann sind die Diagonalen $[D_{n} B_{n}]$ und $[A_{n} C_{n}]$ gleich lang, das bedeutet $4 LE$ .
Funktion gleich $4$ setzen und mithilfe der Mitternachtsformel auflösen:
$- 0,4 x^{2} + 1,3 x + 5,4$ $=$ $4$ $- 4$
$- 0,4 x^{2} + 1,3 x + 1,4$ $=$ $0$
Die quadratische Gleichung wird mit der Mitternachtsformel gelöst:
$a = - 0,4, b = 1,3$ und $c = 1,4$
$x_{1,2}$ $=$ $\frac{- 1,3 \pm \sqrt{{1,3}^{2} - 4 \cdot (- 0,4) \cdot 1,4}}{2 \cdot (- 0,4)}$
$=$ $\frac{- 1,3 \pm \sqrt{1,69 + 2,24}}{- 0,8}$
$=$ $\frac{- 1,3 \pm \sqrt{3,93}}{- 0,8}$
$x_{1} = - 0,85$ und $x_{2} = 4,10$
$𝕃 = {- 0,85; 4,10}$
Bei diesen Werten schneiden sich die Diagonalen der Quadrate.
Die x-Koordinaten der Punkte $B_{2}$ und $B_{3}$ liegen 2 Einheiten weiter rechts (Symmetrieeigenschaft von Quadraten):
$X_{B_{2}} = - 0,85 + 2 = 1,15$
$X_{B_{3}} = 4,10 + 2 = 6,10$
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Nebenstehende Skizze zeigt das Fünfeck $A B C D E$ mit dem Punkt $F \in [A E]$ . Es gilt: $D E = 4 cm; B F = 8 cm; ∡ A E D = ∡ A F B = 90 °; [C F] | | [D E]$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
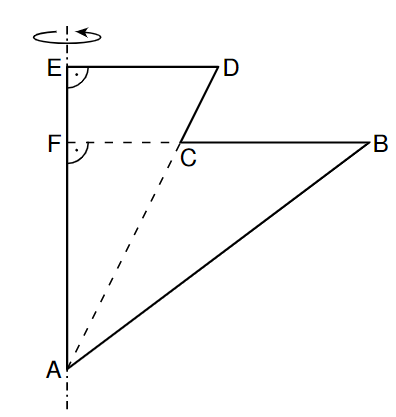
Der Kegel, der durch Rotation des Dreiecks $A D E$ um die Achse $A E$ entsteht, hat ein Volumen von $134 {cm}^{3}$ . Berechnen Sie die Höhe dieses Kegels.
$[$ Ergebnis: $A E = 8,00 cm$ $]$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kegelvolumen, Strahlensatz
Teilaufgabe a
Höhe des Kegels mit Rotationskörper Dreieck $A D E$ um $[A E]$ :
$V_{K e g e l}$ $=$ $\frac{1}{3} \cdot π \cdot r^{2} \cdot h$
↓
Bekannte Größen einsetzen.
$134 {cm}^{3}$ $=$ $\frac{1}{3} \cdot π \cdot (4 cm)^{2} \cdot h$ $\cdot 3 | : (4 cm)^{2} | : π$
↓
Nach der Unbekannten auflösen.
$h$ $=$ $\frac{134 {cm}^{3} \cdot 3}{π \cdot (4 cm)^{2}}$
↓
Zusammenfassen.
$\approx$ $8,00 cm$

Die Strecke $[A F]$ ist um $25 %$ kürzer als die Strecke $[A E]$ .
Berechnen Sie das Volumen $V$ des Rotationskörpers, der durch Rotation des Fünfecks $A B C D E$ um die Achse $A E$ entsteht.
$[$ Zwischenergebnis: $C F = 3,00 cm$ $]$

Teilaufgabe b
Länge der Strecke [AF]:
$A F = A E \cdot \frac{75}{100} = 8,00 cm \cdot \frac{75}{100} = 6,00 cm$
Volumen des Rotationskörpers:
$C F$ mithilfe des Strahlensatzes:
$\frac{C F}{D E}$ $=$ $\frac{A F}{A E}$ $\cdot D E$
$C F$ $=$ $\frac{A F \cdot D E}{A E}$
$=$ $\frac{6 cm \cdot 4 cm}{8 cm}$
$=$ $3,00 cm$
$V_{A B C D E}$ $=$ $V_{A D E} + V_{A B F} - V_{A C F}$
$=$ $(134 + \frac{1}{3} \cdot π \cdot 8^{2} \cdot 6 - \frac{1}{3} \cdot π \cdot 3^{2} \cdot 6) {cm}^{3}$
$=$ $(134 + 402,12 - 56,55) {cm}^{3}$
$\approx$ $479,57 {cm}^{3}$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

$y$	$=$	$0,4 {(x - 2)}^{2} - 3$
	↓	Binomische Formel anwenden.
	$=$	$0,4 (x^{2} - 4 x + 4) - 3$
	↓	Klammer ausmultiplizieren.
	$=$	$0,4 x^{2} - 1,6 x + 1,6 - 3$
	↓	Zusammenfassen.
	$=$	$0,4 x^{2} - 1,6 x - 1,4$

$y (2)$	$=$	$0,4 \cdot 2^{2} - 1,6 \cdot 2 - 1,4$
	$=$	$0,4 \cdot 4 - 3,2 - 1,4$
	$=$	$1,6 - 3,2 - 1,4$
	$=$	$- 3$

$[A_{n} C_{n}]$	$=$	$(- 0,3 x + 4 - (0,4 x^{2} - 1,6 x - 1,4)) LE$
	↓	Klammer auflösen.
	$=$	$(- 0,3 x + 4 - 0,4 x^{2} + 1,6 x + 1,4) LE$
	↓	Zusammenfassen.
	$=$	$(- 0,4 x^{2} + 1,3 x + 5,4) LE$

$A_{Drache}$	$=$	$\frac{e \cdot f}{2}$
	↓	Einsetzen.
	$=$	$\frac{(4 \cdot (- 0,4 x^{2} + 1,3 x + 5,4)) LE}{2}$
	↓	Kürzen.
	$=$	$(2 \cdot (- 0,4 x^{2} + 1,3 x + 5,4)) LE$
	↓	Klammer ausrechnen.
	$=$	$(- 0,8 x^{2} + 2,6 x + 10,8) LE$

$y oder A_{\max}$	$=$	$c - \frac{b^{2}}{4 \cdot a}$
	$=$	$10,8 - \frac{{2,6}^{2}}{4 \cdot (- 0,8)}$
	$=$	$10,6 - \frac{169}{80}$
	$\approx$	$12,91 FE$
	$<$	$15 FE$

$- 0,4 x^{2} + 1,3 x + 5,4$	$=$	$4$	$- 4$
$- 0,4 x^{2} + 1,3 x + 1,4$	$=$	$0$

$x_{1,2}$	$=$	$\frac{- 1,3 \pm \sqrt{{1,3}^{2} - 4 \cdot (- 0,4) \cdot 1,4}}{2 \cdot (- 0,4)}$
	$=$	$\frac{- 1,3 \pm \sqrt{1,69 + 2,24}}{- 0,8}$
	$=$	$\frac{- 1,3 \pm \sqrt{3,93}}{- 0,8}$

$V_{K e g e l}$	$=$	$\frac{1}{3} \cdot π \cdot r^{2} \cdot h$
	↓	Bekannte Größen einsetzen.
$134 {cm}^{3}$	$=$	$\frac{1}{3} \cdot π \cdot (4 cm)^{2} \cdot h$	$\cdot 3 \| : (4 cm)^{2} \| : π$
	↓	Nach der Unbekannten auflösen.
$h$	$=$	$\frac{134 {cm}^{3} \cdot 3}{π \cdot (4 cm)^{2}}$
	↓	Zusammenfassen.
	$\approx$	$8,00 cm$

$\frac{C F}{D E}$	$=$	$\frac{A F}{A E}$	$\cdot D E$
$C F$	$=$	$\frac{A F \cdot D E}{A E}$
	$=$	$\frac{6 cm \cdot 4 cm}{8 cm}$
	$=$	$3,00 cm$

$V_{A B C D E}$	$=$	$V_{A D E} + V_{A B F} - V_{A C F}$
	$=$	$(134 + \frac{1}{3} \cdot π \cdot 8^{2} \cdot 6 - \frac{1}{3} \cdot π \cdot 3^{2} \cdot 6) {cm}^{3}$
	$=$	$(134 + 402,12 - 56,55) {cm}^{3}$
	$\approx$	$479,57 {cm}^{3}$

Nachtermin Teil A

Teilaufgabe a

asin⁡(α)=bsin⁡(β)

AMsin⁡(36°)=AP1sin⁡(110°)

Teilaufgabe b

Teilaufgabe a

Teilaufgabe b

Teilaufgabe c

Teilaufgabe d

Teilaufgabe a

Teilaufgabe b

$\frac{a}{\sin (α)} = \frac{b}{\sin (β)}$

$\frac{A M}{\sin (36 °)} = \frac{A P_{1}}{\sin (110 °)}$