Aufgaben zu Schrägbildern und Mantelflächen von Prismen und Zylindern

1
Zeichne das Schrägbild und das Netz eines liegenden geraden Prismas mit dreieckiger Grundfläche. Das Prisma soll auf der Fläche liegen, die die Dreiecksseite $A B = c = 6 cm$ und die Höhe $h = 8 cm$ des Prismas enthält. Die anderen Seiten des Dreiecks haben die Längen $B C = a = 6,4 cm$ und $A C = b = 4,1 cm$ . Das Maß des Verzerrungswinkels ist $α = 45^{\circ}$ und der Verzerrungsmaßstab (Verkürzungsfaktor) ist $k = \frac{1}{2}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder zeichnen
Schrägbild des Prismas
Konstruktion der Grundfläche (Dreieck) des Prismas
1. Zeichne die Seite $A B$ mit der Originallänge $c = 6 cm$ .
2. Zeichne um $A$ einen Kreisbogen mit dem Radius $r_{1} = A C = 4,1 cm$ .
3. Zeichne um $B$ einen Kreisbogen mit dem Radius $r_{2} = B C = 6,4 cm$ .
4. Die beiden Kreisbögen schneiden sich im Punkt $C$ .
5. Verbinde die Punkte $A$ mit $C$ und $B$ mit $C$ .
Konstruktion der Seitenflächen (Rechteck) des Prismas
6. Lege das Geodreieck im Punkt $B$ an und markiere den Verzerrungswinkel $α = 45^{\circ}$ (hier Punkt $P$ am Geodreieck).
7. Verbinde den Punkt $B$ mit $P$ .
8. Zeichne um $B$ einen Kreisbogen mit dem Radius $r_{3} = 4 cm$ . Das Längenmaß $4 cm$ entspricht der Höhe $h = 8 cm$ des Prismas, die auf die Hälfte verkürzt gezeichnet wird.
9. Der Kreisbogen schneidet den freien Schenkel des Winkels $α$ im Punkt $E$ .
Zur besseren Übersichtlichkeit werden bei jedem Konstruktionsschritt einige Hilfslinien und Hilfspunkte entfernt.
10. Verschiebe die Strecke $[B E]$ parallel, so dass sie im Punkt $C$ beginnt und eine Länge von $4 cm$ besitzt.
11. Verschiebe die Strecke $[B E]$ parallel, so dass sie im Punkt $A$ beginnt und eine Länge von $4 cm$ besitzt. (Die letzte Strecke ist gestrichelt, da diese Kante aus diesem Blickwinkel nicht sichtbar ist).
Konstruktion der Deckfläche (Dreieck) des Prismas
12. Verbinde die Endpunkte der parallel verschobenen Strecken. Achte dabei auf die nicht sichtbaren Strecken $[D E]$ und $[D F]$ .
Dein Schrägriss eines liegenden geraden Prismas mit dreieckiger Grundfläche ist fertig.
Netz des Prismas
Konstruktion der Seitenflächen des Prismas
1. Zeichne ein Rechteck mit den Seitenlängen $A B = 6 cm$ und $A D = 8 cm$ ( $A D$ entspricht der Höhe $h$ des Prismas).
2. Zeichne an das Rechteck $A B E D$ nach links anschließend das Rechteck $C^{'} A D F^{'}$ (dabei ist $C^{'} A = 4,1 cm$ ) und nach rechts anschließend das Rechteck $B C^{''} F^{''} E$ (dabei ist $B C^{''} = 6,4 cm$ .
Konstruktion der Grund-und Deckfläche des Prismas
3. An der Seite $[D E]$ liegt das Dreieck $D E F$ an. An der Seite $[A B]$ liegt das Dreieck $A B C$ an.
4. Zeichne um die Punkte $D$ und $A$ je einen Kreisbogen mit dem Radius $r = C^{'} A = 4,1 cm$ (Dreieckseite $b$ ).
5. Zeichne um die Punkte $B$ und $E$ je einen Kreisbogen mit dem Radius $r = B C^{''} = 6,4 cm$ (Dreieckseite $a$ ).
5. Der Kreisbogen um $A$ und der Kreisbogen um $B$ schneiden sich im Punkt $C$ des Dreiecks $A B C$ .
6. Der Kreisbogen um $D$ und der Kreis um $E$ schneiden sich im Punkt $F$ des Dreiecks $D E F$ .
Zur besseren Übersichtlichkeit werden einige Hilfslinien entfernt.
7. Verbinde die Punkte $A$ mit $C$ und $B$ mit $C$ .
8. Verbinde die Punkte $D$ mit $F$ und $E$ mit $F$ .
Dein Netz eines geraden Prismas mit dreieckiger Grundfläche ist fertig.
2
Zeichne das Schrägbild und das Netz eines liegenden geraden Prismas. Die Grundfläche des Prismas ist ein regelmäßiges Fünfeck mit einer Seitenlänge von $a = 3 cm$ . Das Prisma ist $12 cm$ hoch. Das Maß des Verzerrungswinkels ist $α = 45^{\circ}$ und der Verzerrungsmaßstab (Verkürzungsfaktor) ist $k = \frac{1}{2}$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Schrägbilder zeichnen
Schrägbild des Prismas
Konstruktion der Grundfläche (Fünfeck) des Prismas
Bei der Konstruktion eines regelmäßigen Fünfecks beginnst du mit der Konstruktion des sogenannten Bestimmungsdreiecks.
Für die Konstruktion des Bestimmungsdreiecks benötigst du einige Informationen:
Ein reguläres Fünfeck kannst du in 5 gleichschenklige Dreiecke zerlegen, so wie es die nebenstehende Skizze zeigt.
Den Mittelpunktswinkel erhältst du, indem $360^{\circ}$ durch die Anzahl der Ecken (hier 5) geteilt wird $\Rightarrow$ $360^{\circ} : 5 = 72^{\circ}$ .
Da die Winkelsumme im Dreieck $180^{\circ}$ beträgt, haben die beiden Basiswinkel $φ$ zusammen eine Größe von $180^{\circ} - 72^{\circ} = 108^{\circ}$ , d.h. jeder Basiswinkel ist $φ = \frac{108^{\circ}}{2} = 54^{\circ}$ groß.
Konstruiere also zunächst ein Dreieck mit der gegebenen Seitenlänge $a = 3 cm$ des Fünfecks als Basis und den anliegenden Basiswinkeln $φ = 54^{\circ}$ .
1. Zeichne die Seite $[A B]$ mit der Originallänge $a = 3 cm$ .
2. Lege das Geodreieck im Punkt $A$ an und markiere den Winkel $φ = 54^{\circ}$ (hier Punkt $P$ am Geodreieck).
3. Lege das Geodreieck im Punkt $B$ an und markiere den Winkel $φ = 54^{\circ}$ (hier Punkt $Q$ am Geodreieck).
4. Verbinde Punkt $A$ mit Punkt $P$ und Punkt $B$ mit Punkt $Q$ .
5. Der Schnittpunkt der beiden Schenkel ist der Mittelpunkt $M$ des Fünfecks.
Zur besseren Übersichtlichkeit werden bei jedem Konstruktionsschritt einige Hilfslinien und Hilfspunkte entfernt.
6. Damit ist die Konstruktion des Bestimmungsdreiecks für das Fünfeck abgeschlossen.
7. Zeichne einen Kreis mit Mittelpunkt $M$ und $r_{1} = M A$ .
8. Zeichne im Punkt B einen Kreisbogen mit $r_{2} = 3 cm$ (das ist die Länge der Fünfeckseite). Er schneidet den Kreis mit Mittelpunkt $M$ im Punkt $C$ .
9. Zeichne im Punkt C einen Kreisbogen mit $r_{3} = 3 cm$ . Er schneidet den Kreis mit Mittelpunkt $M$ im Punkt $D$ .
10. Zeichne im Punkt D einen Kreisbogen mit $r_{4} = 3 cm$ . Er schneidet den Kreis mit Mittelpunkt $M$ im Punkt $E$ .
11. Verbinde die Punkte $B$ mit $C$ , $C$ mit $D$ , $D$ mit $E$ und $E$ mit $A$ .
Dein regelmäßiges Fünfeck ist fertig.
Konstruktion der Seitenflächen (Rechtecke) des Prismas
12. Lege das Geodreieck im Punkt $B$ an und markiere den Verzerrungswinkel $α = 45^{\circ}$ (hier Punkt $R$ am Geodreieck).
13. Zeichne eine Halbgerade im Punkt $B$ beginnend durch den Punkt $R$ .
14. Zeichne um $B$ einen Kreisbogen mit dem Radius $r = 6 cm$ . Das Längenmaß $6 cm$ entspricht der Höhe $h = 12 cm$ des Prismas, die auf die Hälfte verkürzt gezeichnet wird.
15. Der Kreisbogen schneidet den freien Schenkel des Winkels $α$ im Punkt $G$ .
16. Hilfslinien, Hilfspunkte und der eingezeichnete Winkel wurden entfernt.
17. Verschiebe die Strecke $[B G]$ parallel, so dass sie im Punkt $C$ beginnt und $6 cm$ lang ist.
18. Verschiebe die Strecke $[B G]$ parallel, so dass sie im Punkt $D$ beginnt und $6 cm$ lang ist.
19. Verschiebe die Strecke $[B G]$ parallel, so dass sie im Punkt $E$ beginnt und $6 cm$ lang ist.
20. Verschiebe die Strecke $[B G]$ parallel, so dass sie im Punkt $A$ beginnt und $6 cm$ lang ist. (Die letzte Strecke sollte gestrichelt werden, da diese Kante in dieser Ansicht nicht sichtbar ist).
Die Deckfläche (Fünfeck) des Prismas
21. Verbinde die Endpunkte der parallel verschobenen Strecken. Achte dabei auf die nicht sichtbaren Strecken $[F G]$ und $[F J]$ .
Dein Schrägbild eines liegenden geraden Prismas mit einem regelmäßiges Fünfeck als Grundfläche ist fertig.
Netz des Prismas
Konstruktion der Seitenflächen (Rechtecke) des Prismas
1. Zeichne nebeneinanderliegend fünf Rechtecke mit den Maßen $a = 3 cm$ und $h = 12 cm$ .
Konstruktion der Grund-und Deckfläche (Fünfecke) des Prismas
2. Wähle eines der fünf Rechtecke aus und konstruiere z.B. an die Seite $[B C]$ ein regelmäßiges Fünfeck. Verfahre entsprechend der Schritte 2 bis 11 (Konstruktion eines regelmäßigen Fünfecks).
Du hast auf der einen Seite des Rechteck $B C I H$ ein regelmäßiges Fünfeck mit der Seitenlänge $a = 3 cm$ konstruiert.
3. Führe die Konstruktionsschritte 2 bis 11 an der Seite $[H I]$ auf der gegenüberliegenden Seite des Rechtecks $B C I H$ durch.
Dein Netz eines geraden Prismas mit einem regelmäßiges Fünfeck als Grundfläche ist fertig.
Hinweis:
Die beiden Fünfecke müssen nicht unbedingt an die Seite $[B C]$ bzw. $[H I]$ des Rechtecks konstruiert werden.
Du kannst das eine Fünfeck z.B. an die orangefarbige Seite $[A B]$ (oder jede beliebige andere orangefarbige Seite) angrenzen lassen.
Das zweite Fünfeck kann z.B. an die grüne Seite $[J K]$ (oder jede beliebige andere grüne Seite) angrenzen.
3
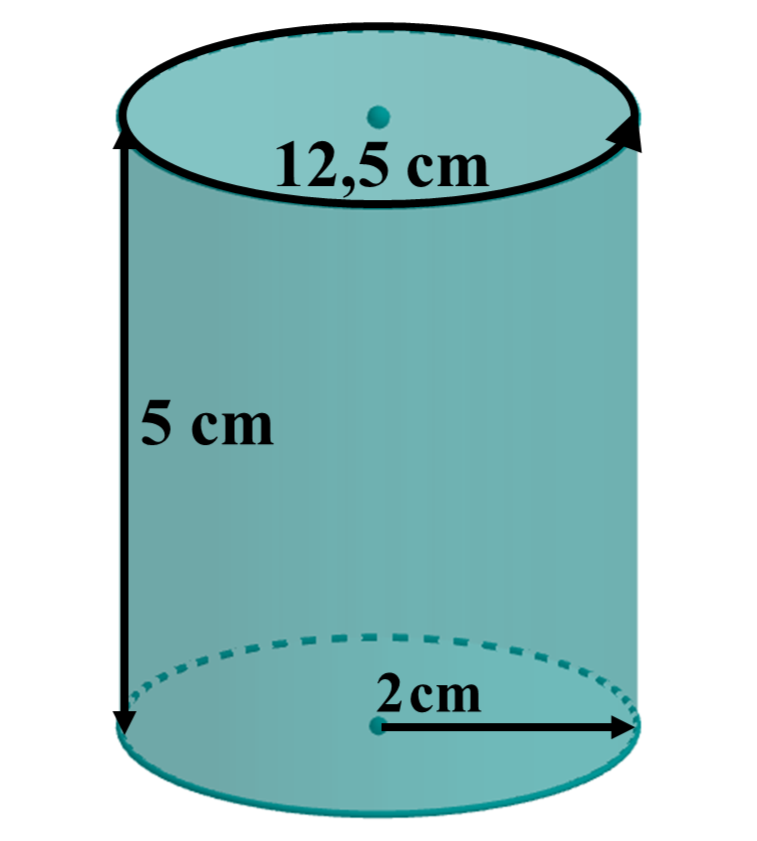
Ein Zylinder hat eine Höhe von $5 𝖼𝗆$ . Die Grundfläche (also der Kreis) hat einen Durchmesser von $4 𝖼𝗆$ und einen Umfang von $12,5 𝖼𝗆$ .
Zeichne das Körpernetz des Zylinders.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Körpernetze
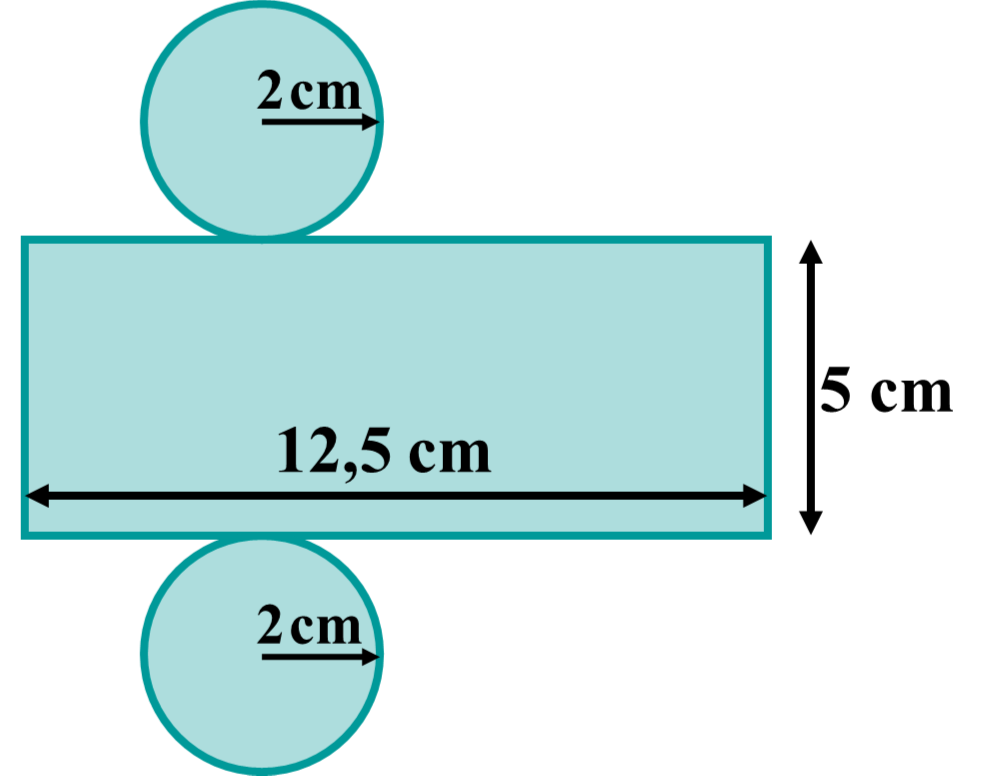
Das Körpernetz des Zylinders besteht aus 3 Geometrischen Figuren. Darunter sind zwei gleich große Kreise und ein Rechteck.
Die Kreise bilden den Deckel und den Boden, das Rechteck den Mantel.
Der Radius der Kreise ergibt sich indem man den Durchmesser halbiert:
$r = \frac{4 𝖼𝗆}{2} = 2 𝖼𝗆$
Die Mittelpunkte der Kreise haben also einen Abstand von $2 𝖼𝗆$ zum Rechteck.
Das Rechteck hat eine Breite von $5 𝖼𝗆$ . Das entspricht dem Abstand zwischen den Kreisen, also der Höhe des Zylinders.
Die Länge von $12,5 𝖼𝗆$ von dem Rechteck ergibt sich aus dem Umfang eines Kreises.
4
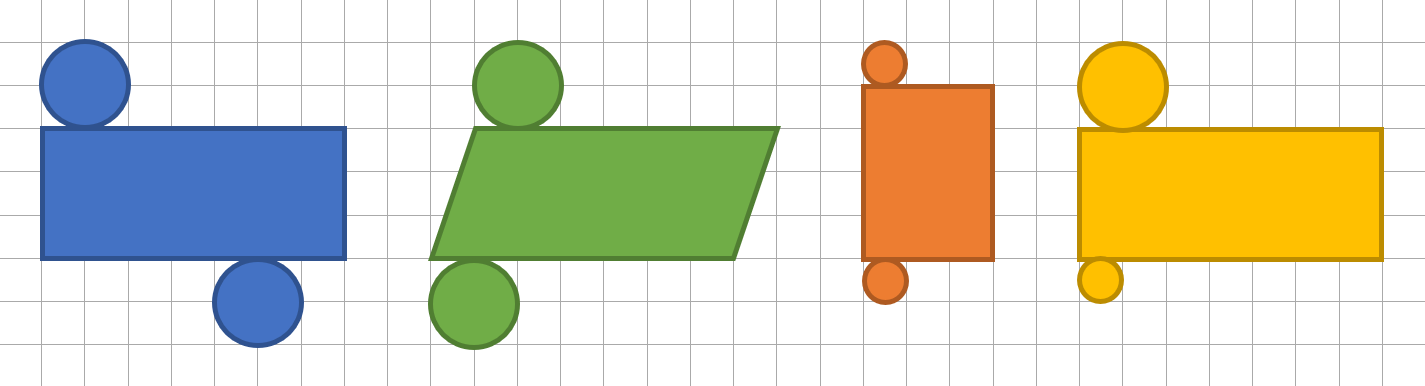
Entscheide und begründe, welche Netze einen Zylinder darstellen könnten:
Netz blau
Netz grün
Netz orange
Netz gelb

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder
Netz blau
Dies könnte ein Netz eines Zylinders sein. Man hat 2 deckungsgleiche Kreise als Deck- und Grundfläche. Außerdem scheint auf den ersten Blick, dass die Breite der Mantelfläche ungefähr der Länge des Umfangs entspricht.
Netz grün
Du hast gelernt, dass die ausgerollte Mantelfläche eines Zylinders ein Rechteck darstellt. Deswegen ist dies kein klassisches Netz eines Zylinders. Wenn du jetzt aber von rechts ein rechtwinkliges Dreieck "abschneidest" und links wieder dransetzt, dann erkennst du dass ein Rechteck entsteht.
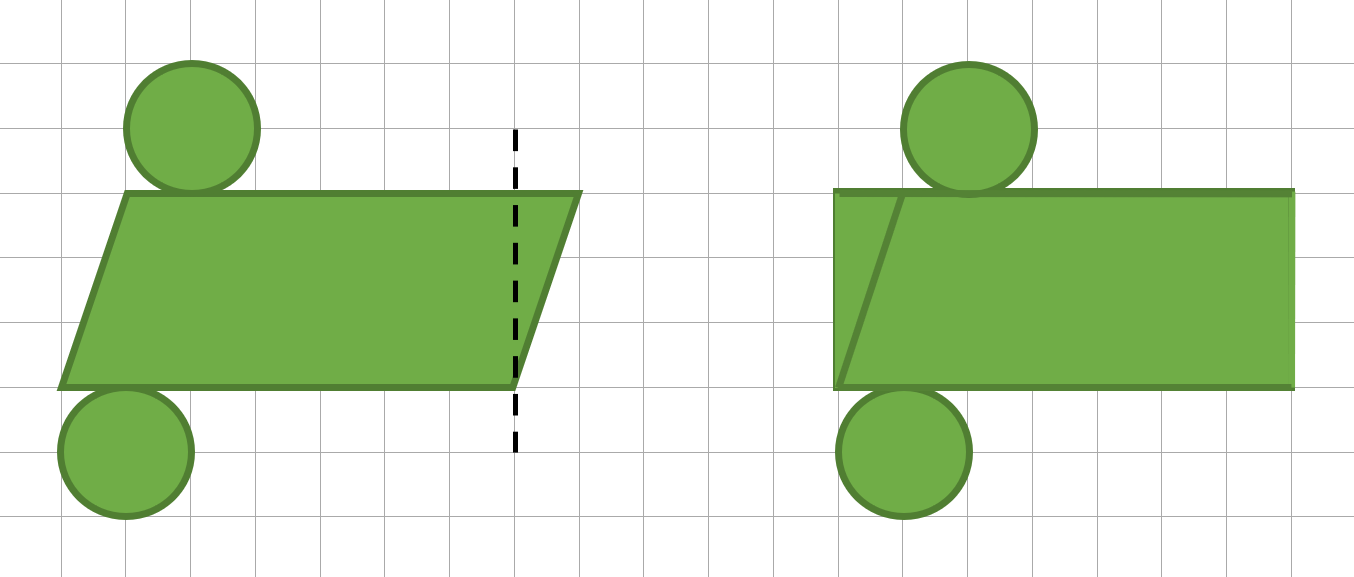
Zusätzlich zu dem entstandenen Rechteck hast du 2 deckungsgleiche Kreise als Deck- und Grundfläche. Du kannst also davon ausgehen, dass wenn man das Netz zusammenbaut, ein Zylinder entsteht.
Netz orange
Dies könnte ein Netz eines Zylinders sein. Man hat 2 deckungsgleiche Kreise als Deck- und Grundfläche. Außerdem scheint auf den ersten Blick, dass die Breite der Mantelfläche ungefähr der Länge des Umfangs entspricht.
Netz gelb
Dies ist kein Netz von einem Zylinder, da die Deck- und die Grundfläche nicht deckungsgleich sind.
5
Wähle alle Bilder aus, die ein Zylindernetz darstellen?
Bild 1
Bild 2
Bild 3
Bild 4
Bild 5
Bild 6
Bild 7

Für diese Aufgabe benötigst Du folgendes Grundwissen: Körpernetze
Bild 1
Antwort: Kein Zylindernetz
In diesem Bild ist die das Rechteck länger als der Umfang der Kreise. Die Länge der einen Mantelseite (an der sich die Kreise befinden) ist etwa vier mal so groß wie der Durchmesser $d$ des Kreises. Der Kreis passt somit in ein Quadrat mit der Seitenläge $d$ . Anschaulich ist klar, dass der Umfang des Quadrates größer als der Kreisumfang ist. Deshalb kann es kein Zylindernetz sein.
Bild 2
Antwort: Kein Zylindernetz
Der Umfang des Grund-(Deck) Kreises ist viel größer als die Länge der Seite an der sich die Kreise befinden. Deshalb kann es kein Zylindernetz sein.
Bild 3
Antwort: Zylindernetz
Hier entspricht die Länge der Rechteckseite an der sich die Kreise befinden dem Kreisumfang. Die Kreise sind an zwei gegenüberliegenden Rechteckseiten angeordnet. Deshalb ist es ein Zylindernetz.
Bild 4
Antwort: Kein Zylindernetz
Die Kreise müssen an zwei gegenüberliegenden Rechteckseiten angeordnet sein. Hier sind sie auf einer Seite angeordnet. Deshalb kann es kein Zylindernetz sein.
Bild 5
Antwort: Zylindernetz
Hier entspricht die Länge der Rechteckseite an der sich die Kreise befinden dem Kreisumfang. Die beiden Kreise liegen zudem an zwei gegenübberliegenden Rechtecksseiten. Deshalb ist es ein Zylindernetz.
Bild 6
Antwort: Kein Zylindernetz
Die beiden Kreise haben verschiedene Radien (Grund-und Deckkreis müssen deckungsgleich sein).
Deshalb kann es kein Zylindernetz sein.
Bild 7
Antwort: Kein Zylindernetz
Die Kreise schneiden die Mantelfläche. Die Kreise dürfen nur einen gemeinsamen Berührpunkt mit der Mantelfläche haben. Deshalb kann es kein Zylindernetz sein.