Aufgaben zur Volumenberechung bei zusammengesetzten Körpern und Sachaufgaben

1
Berechne durch geschicktes Aufteilen das Volumen des gegebenen Körpers.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumenberechnung bei zusammengesetzten Körpern
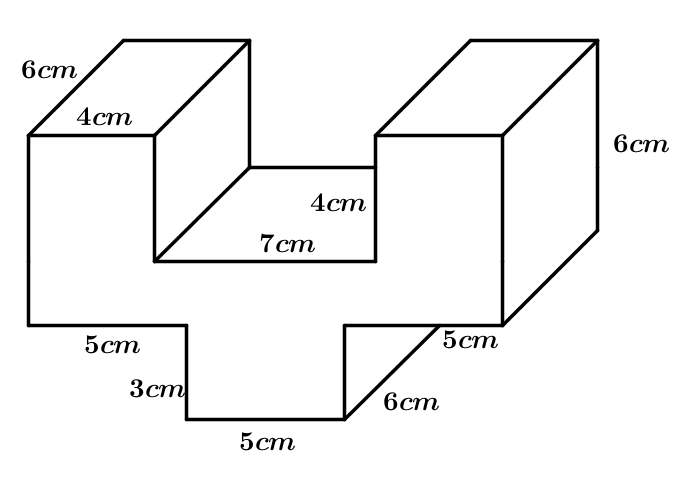
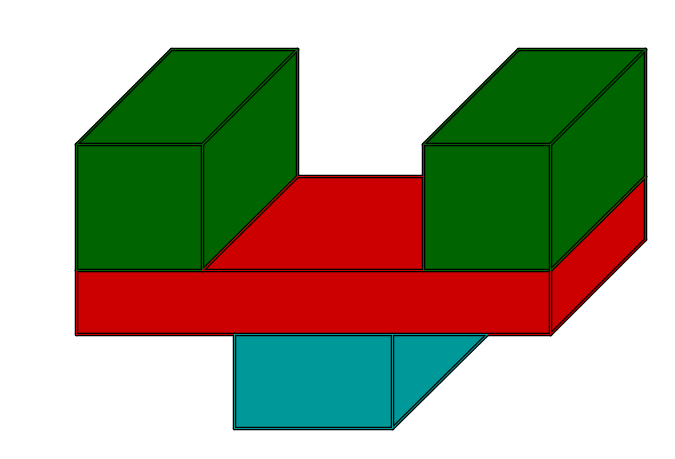
Zerteile zuerst den Körper in Quader.
Berechne nun jeweils das Volumen der einzelnen Quader.
Oberster Quader: $V_{Quader oben} = 3 cm \cdot 4 cm \cdot 3 cm = 36 {cm}^{3}$
Mittlerer Quader: $V_{Quader Mitte} = 11 cm \cdot 3 cm \cdot 4 cm = 132 {cm}^{3}$
Unterer Quader: $V_{Quader unten} = 3 cm \cdot 4 cm \cdot 2 cm=24 {cm}^{3}$
Jetzt musst du nur noch alle Volumen miteinander addieren.
$V_{gesamt} = 36 {cm}^{3} + 132 {cm}^{3} + 24 {cm}^{3} = 192 {cm}^{3}$
2
Berechne durch geschicktes Aufteilen das Volumen des gegebenen Körpers. Gib das Ergebnis auf eine Stelle nach dem Komma gerundet OHNE Größeneinheit an!

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumensberechnung bei zusammengesetzten Körpern
Berechne als Erstes einen der Zylinder.
$(2 cm)^{2} \cdot π \cdot 3 cm \approx 37,7 {cm}^{3}$
Berechne nun den Quader.
$13 cm \cdot 4 cm \cdot 3 cm = 156 {cm}^{3}$
Nun musst du nur noch dreimal den Zylinder mit dem Quader addieren.
$3 \cdot 37,7 {cm}^{3} + 156 {cm}^{3} \approx 269.1 {cm}^{3}$
3
Berechne das Volumen des folgenden Körpers durch geschicktes Aufteilen in Quader.

Teile den Körper zuerst in 4 Quader ein.
Rechne nun das Volumen des untersten Quaders aus.
$5 cm \cdot 6 cm \cdot 3 cm = 90 {cm}^{3}$
Rechne jetzt den roten Quader aus.
$15 cm \cdot 6 cm \cdot 2 cm = 180 {cm}^{3}$
Rechne nun einen der zwei grünen Quader aus.
$6 cm \cdot 4 cm \cdot 4 cm = 96 {cm}^{3}$
Jetzt musst du nur noch alle Quader zusammenrechnen. Allerdings musst du den grünen Quader zweimal nehmen.
$90 {cm}^{3} + 180 {cm}^{3} + 2 \cdot 96 {cm}^{3} = 462 {cm}^{3}$
4
Welches Volumen hat ein $4,5 m$ hohes Haus mit der Breite $4 m$ und der Länge $7 m$ , wenn das Dachgeschoss $2 m$ hoch ist?
Quelle: torange.biz, CC-BY-SA-4.0

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen zusammengesetzter Körper
Quelle: torange.biz, CC-BY-SA-4.0
Du kannst das Volumen von diesem Haus auf zwei Arten berechnen:
Entweder als ein Prisma mit der ganzen Vorderseite des Hauses als Grundfläche
oder als einen zusammengesetzten Körper aus einem Quader (unterer Teil des Hauses) und einem Prisma mit einem Dreieck als Grundfläche (das Dach).
In dieser Lösung wird das Volumen für den zusammengesetzten Körper berechnet.
Volumen des Quaders (unterer Hausteil)
Gegeben: Länge des Quaders = $7 m$ Breite des Quaders = $4 m$
Die Höhe des Quaders musst du erst noch ausrechnen.
Höhe des Quaders = ?
Die Höhe berechnest du, indem du von der Gesamthöhe des Hauses ( $4,5 m$ ) die Höhe des Dachs ( $2 m$ ) abziehst.
Höhe des Quaders = $4,5 m - 2 m = 2,5 m$
Jetzt kannst du das Volumen des Quaders berechnen.
$V_{Quader} = Länge \cdot Breite \cdot Höhe = 7 m \cdot 4 m \cdot 2,5 m = 70 m^{3}$
Volumen des Prismas (Dach)
Gegeben: Länge des Dachs = $7 m$ Breite des Dachs = $4 m$ Höhe des Dachs = $2 m$
Für das Volumen des Prismas benötigst du zuerst seine Grundfläche. Diese ist hier ein Dreieck. Die Höhe des Dreiecks ist die Dachhöhe und die Grundseite ist die Breite des Dachs.
$G_{Prisma} = \frac{1}{2} \cdot Breite \cdot Höhe = \frac{1}{2} \cdot 4 m \cdot 2 m = 4 m^{2}$
Berechne jetzt das Volumen des Prismas. Beachte, dass die Höhe des Prismas hier die Länge des Dachs ist.
$V_{Prisma} = G_{Prisma} \cdot Länge = 4 m^{2} \cdot 7 m = 28 m^{3}$
Gesamtvolumen des Hauses
$V_{Haus} = \dots ?$
Addiere jetzt die einzelnen Teile, um das Gesamtvolumen zu berechnen.
$V_{Haus} = V_{Quader} + V_{Prisma} = 70 m^{3} + 28 m^{3} = 98 m^{3}$
Antwort: Das Haus hat ein Volumen von $98 m^{3}$ .

Berechne das Volumen und den Oberflächeninhalt des Werkstücks.

Hinweis: Rechne immer mit $π = 3,14.$ Runde auf zwei Kommastellen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Zylinder

Teillösung 1: Volumen

Maße großer Zylinder: $d_{1} = 6 cm$ ; $h_{1} = 3,5 cm$

Der Radius ist halb so lang wie der Durchmesser $\Rightarrow r_{1} = \frac{d_{1}}{2} = 3 cm$ .

Maße kleiner Zylinder: $d_{2} = 2 cm$ ; $h_{2} = 4 cm$

Der Radius ist halb so lang wie der Durchmesser $\Rightarrow r_{2} = \frac{d_{2}}{2} = 1 cm$ .

Das Volumen eines Zylinders berechnest du mit der Formel:

$V_{Z y l i n d e r} = r^{2} \cdot π \cdot h_{k}$

$V_{Z}$	$=$	$V_{g r o ß e r Z y l i n d e r} + V_{k l e i n e r Z y l i n d e r}$
	$=$	$r_{1}^{2} \cdot π \cdot h_{1} + r_{2}^{2} \cdot π \cdot h_{2}$
	$=$	${(3 c m)}^{2} \cdot π \cdot 3,5 c m + {(1 c m)}^{2} \cdot π \cdot 4 c m$
	↓	$π \approx 3,14$
	$\approx$	${(3 c m)}^{2} \cdot 3,14 \cdot 3,5 c m + {(1 c m)}^{2} \cdot 3,14 \cdot 4 c m$
	$=$	$98,91 {c m}^{3} + 12,56 {c m}^{3}$
	$=$	$111,47 {c m}^{3}$

Antwort: Das Werkstück hat ein Volumen von etwa $111,47 {c m}^{3}$ .

Teillösung 2: Oberflächeninhalt

Die Oberfläche dieses Werkstücks besteht aus mehreren Teilflächen:

Kreis, Mantelfläche, Kreisring

Berechne den (sichtbaren) Oberflächeninhalt des großen Zylinders (gr Z) und dann den (sichtbaren) Oberflächeninhalt des kleinen Zylinders (kl Z).

$O_{g r Z}$	$=$	$Grundfläche Kreis + Mantel + Kreisring$
	$=$	$r_{1}^{2} \cdot π + 2 \cdot r_{1} \cdot π \cdot h_{1} + π \cdot (r_{1}^{2} - r_{2}^{2})$
	$=$	$(3 cm)^{2} \cdot π + 2 \cdot 3 cm \cdot π \cdot 3,5 cm + π \cdot ((3 cm)^{2} - (1 cm)^{2})$
	↓	$π \approx 3,14$
	$\approx$	$(3 cm)^{2} \cdot 3,14 + 2 \cdot 3 cm \cdot 3,14 \cdot 3,5 cm + 3,14 \cdot ((3 cm)^{2} - (1 cm)^{2})$
	$=$	$28,26 c m^{2} + 65,94 c m^{2} + 25,12 c m^{2}$
	$=$	$119,32 c m^{2}$

$O_{k l Z}$	$=$	$Mantel + Deckfläche Kreis$
	$=$	$2 \cdot r_{2} \cdot π \cdot h_{k} + r_{2}^{2} \cdot π$
	$=$	$2 \cdot 1 cm \cdot π \cdot 4 cm + (1 cm)^{2} \cdot π$
	↓	$π \approx 3,14$
	$\approx$	$2 \cdot 1 cm \cdot 3,14 \cdot 4 cm + (1 cm)^{2} \cdot 3,14$
	$=$	$25,12 c m^{2} + 3,14 c m^{2}$
	$=$	$28,26 c m^{2}$

$O_{g e s a m t}$	$=$	$O_{g r Z} + O_{k l Z}$
	$=$	$119,32 c m^{2} + 28,26 c m^{2}$
	$=$	$147,58 c m^{2}$

Antwort: Das Werkstück hat einen Oberflächeninhalt von etwa $147,58 c m^{2}$ .

Alternative Berechnung der Oberfläche

Die Oberfläche eines Zylinders berechnest du mit der Formel: $O_{Z y l i n d e r} = 2 \cdot r^{2} \cdot π + 2 \cdot r \cdot π \cdot h_{k}$

Beachte: Die Fläche des $g r \ddot{u} n e n$ Kreises muss vom gesamten Oberflächeninhalt der beiden Zylinder zwei mal abgezogen werden, da diese Fläche sowohl beim großen als auch beim kleinen Zylinder nicht sichtbar ist.

$O_{Z g e s a m t}$	$=$	$O_{g r Z} + O_{k l Z} - 2 \cdot r_{2}^{2} \cdot π$
	$=$	$(2 \cdot r_{1}^{2} \cdot π + 2 \cdot r_{1} \cdot π \cdot h_{1}) + (2 \cdot r_{2}^{2} \cdot π + 2 \cdot r_{2} \cdot π \cdot h_{2}) - 2 \cdot r_{2}^{2} \cdot π$
	↓	Die Fläche des kleinen (grünen) Kreises wurde zwei mal abgezogen.
	$=$	$2 \cdot r_{1}^{2} \cdot π + 2 \cdot r_{1} \cdot π \cdot h_{1} + 2 \cdot r_{2} \cdot π \cdot h_{2}$
	$=$	$2 \cdot (3 cm)^{2} \cdot π + 2 \cdot 3 cm \cdot π \cdot 3,5 cm + 2 \cdot 1 cm \cdot π \cdot 4 cm$
	↓	$π \approx 3,14$
	$\approx$	$2 \cdot (3 cm)^{2} \cdot 3,14 + 2 \cdot 3 cm \cdot 3,14 \cdot 3,5 cm + 2 \cdot 1 cm \cdot 3,14 \cdot 4 cm$
	$\approx$	$56,52 c m^{2} + 65,94 c m^{2} + 25,12 c m^{2}$
	$\approx$	$147,58 c m^{2}$

Antwort: Das Werkstück hat einen Oberflächeninhalt von etwa $147,58 c m^{2}$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

Aufgaben zur Volumenberechung bei zusammengesetzten Körpern und Sachaufgaben

Volumen des Quaders (unterer Hausteil)

Volumen des Prismas (Dach)

Gesamtvolumen des Hauses

Teillösung 1: Volumen

Teillösung 2: Oberflächeninhalt