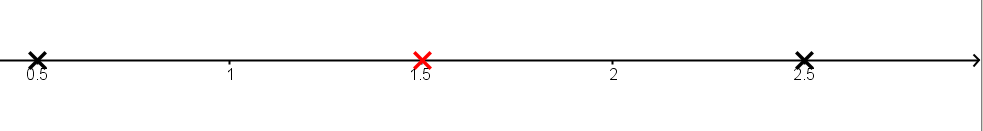Aufgaben zur Berechnung des Scheitelpunktes
- 1
Bestimme mithilfe der Scheitelform den jeweiligen Scheitelpunkt der folgenden Funktionen.
Gib den Scheitelpunkt nach folgendem Beispiel an:
oder .
- 2
Gib jeweils die Koordinaten des Scheitels an.
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
- 3
Bestimme den Scheitelpunkt der folgenden Funktionen.
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
- 4
Bestimme den Scheitelpunkt der Funktion mit der Funktionsgleichung anhand deren Nullstellen.
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
- 5
Bestimme den Scheitelpunkt der Funktion mit der Funktionsgleichung anhand ihrer Nullstellen.
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
- 6
Gib die Koordinaten des Scheitels folgender Funktionen an.
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
- 7
Bestimme den Scheitelpunkt:
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
- 8
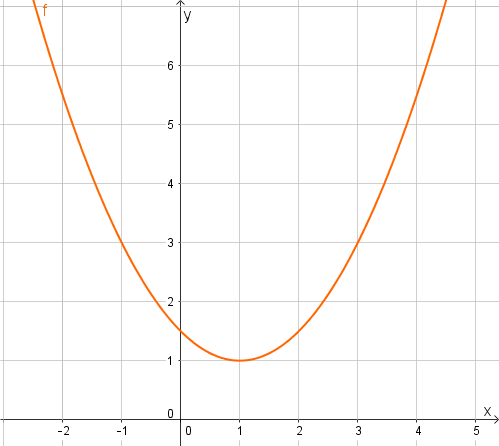
Gib die Scheitelform der Funktionsgleichung der abgebildeten Parabel an.
- 9
Die Firma Habmichgern soll eine Brücke planen. Die Länge soll betragen.
Der Chef der Firma bittet dich, mithilfe der folgenden Funktionsgleichung die maximale Höhe der Brücke zu berechnen.
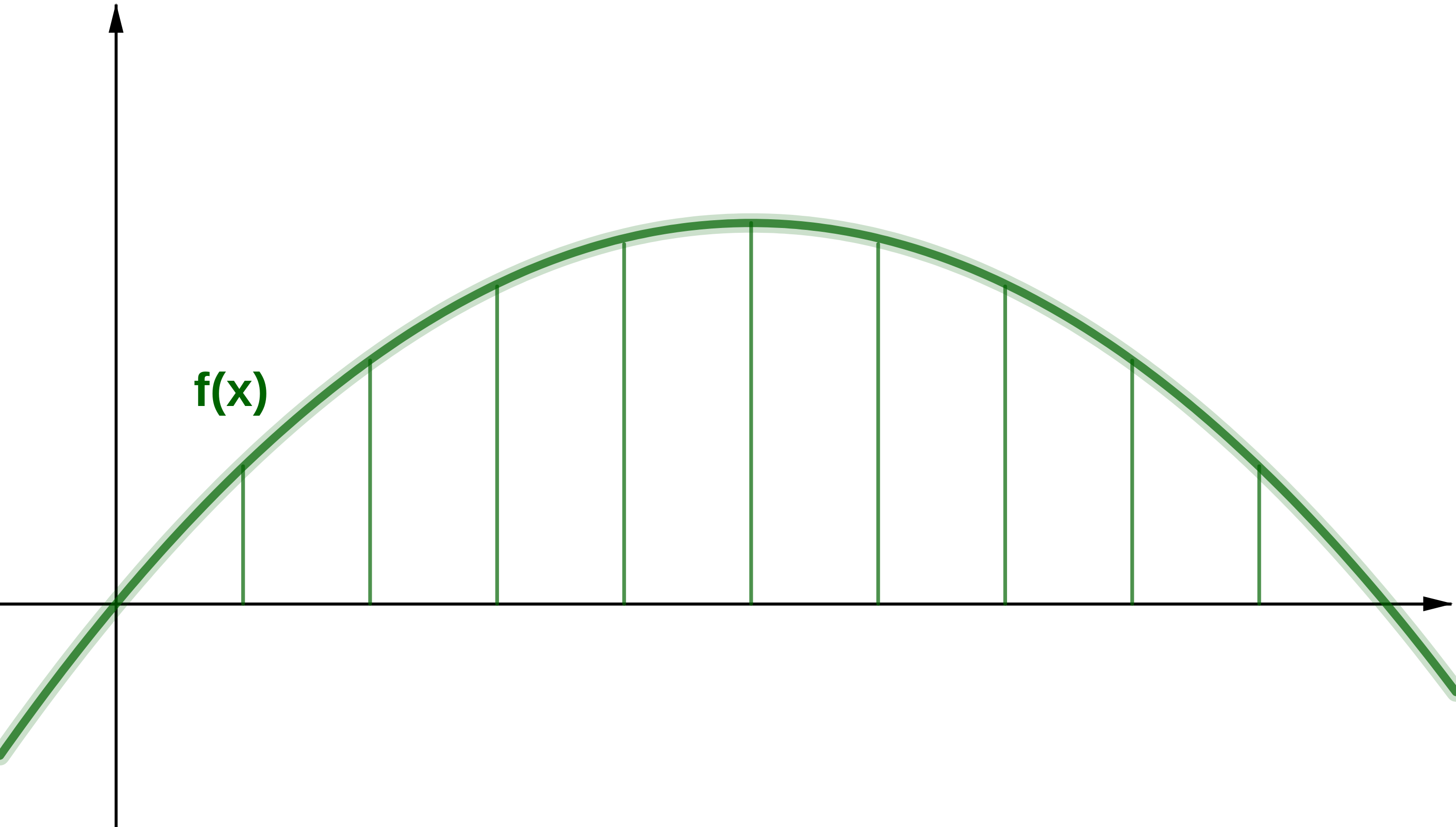 m
m