Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe-Prüfungen
Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
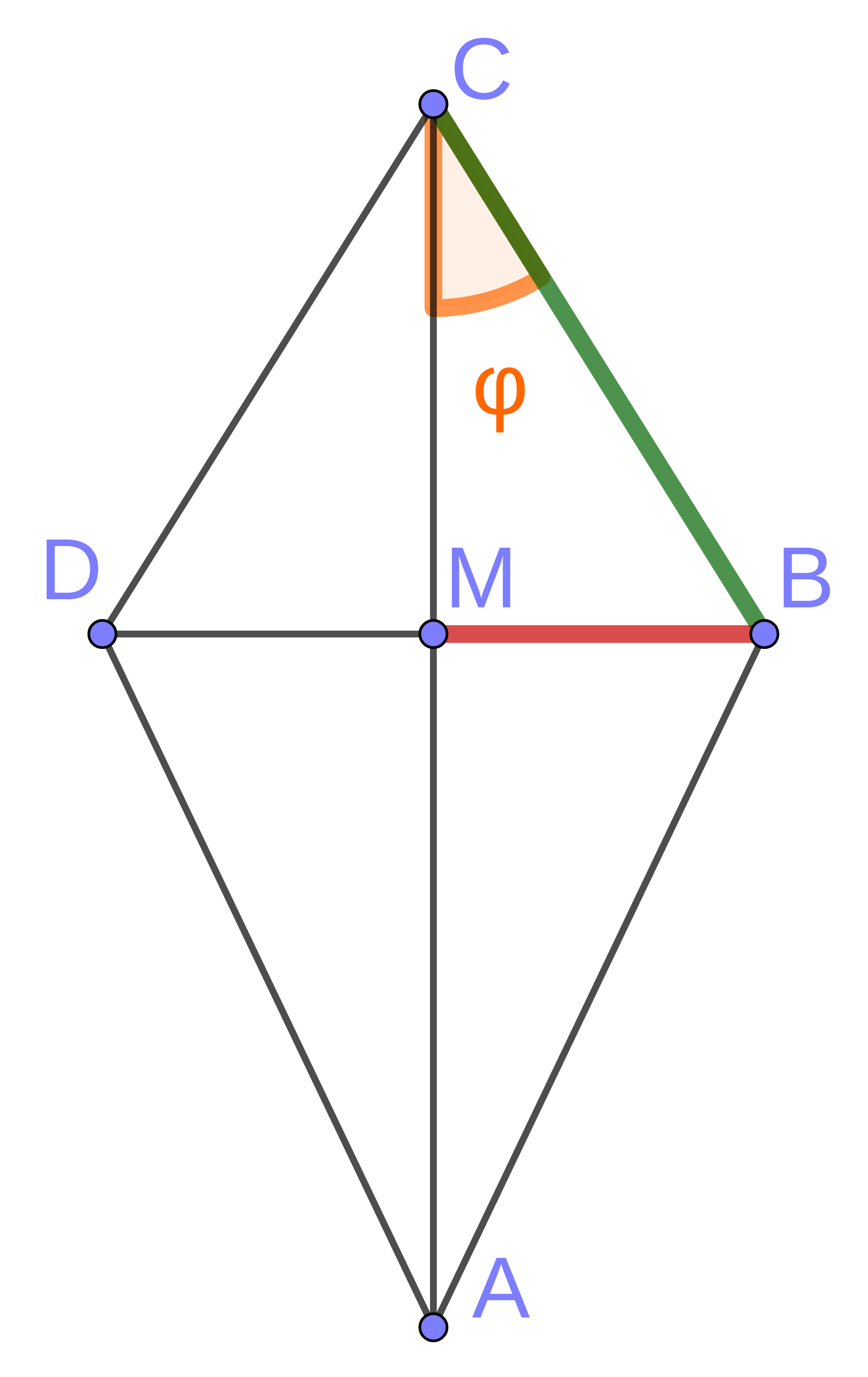
Pia möchte einen Flugdrachen bauen. Dazu erstellt sie nebenstehende Skizze eines Drachenvierecks mit der Symmetrieachse und dem Diagonalenschnittpunkt .
Es gilt:
Runden Sie im Folgenden auf Ganze.
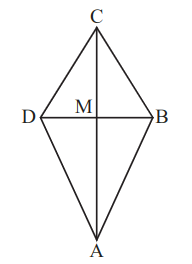
Zeigen Sie rechnerisch, dass für das Maß des Winkels gilt:
Berechnen Sie die Länge der Diagonale und den Flächeninhalt des Drachenvierecks .
Ergebnis:
Da es im Baumarkt nur Holzstäbe mit einer Länge von gibt, beschließt Pia, für die Diagonale diese Länge zu verwenden. Die Diagonale bleibt unverändert.
Kreuzen Sie an, um wie viel Prozent sich der Flächeninhalt dadurch verringert.
- 2
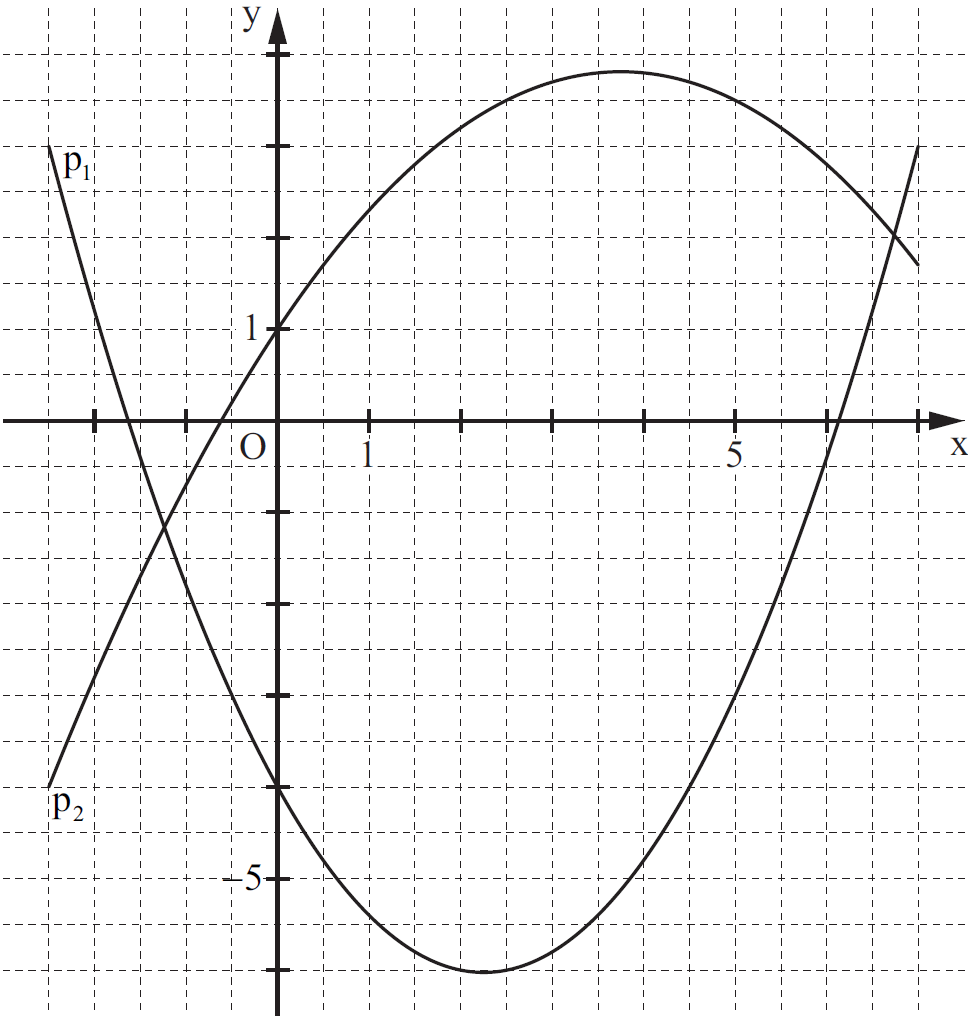
Gegeben sind die Parabeln mit der Gleichung und mit der Gleichung ().
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
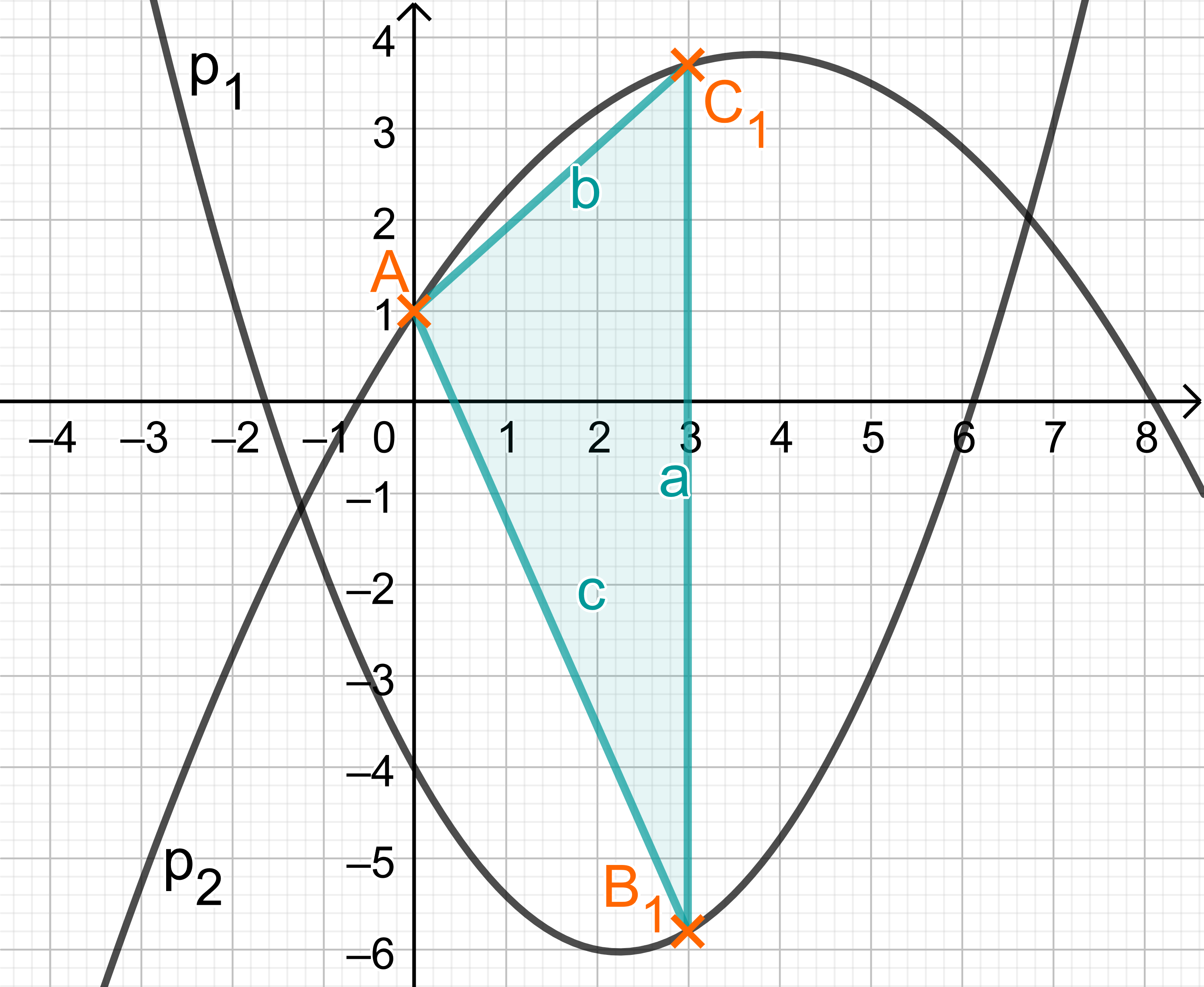
Punkte auf und Punkte auf haben dieselbe Abszisse . Sie sind zusammen mit für Eckpunkte von Dreiecken .
Zeichnen Sie das Dreieck für in das Koordinatensystem zur Aufgabenstellung ein. Zeigen Sie sodann, dass für die Länge der Strecken in Abhängigkeit von der Abszisse der Punkte gilt:
LE.
Begründen Sie, weshalb es unter den Dreiecken kein Dreieck gibt, dessen Seite eine Länge von LE besitzt.
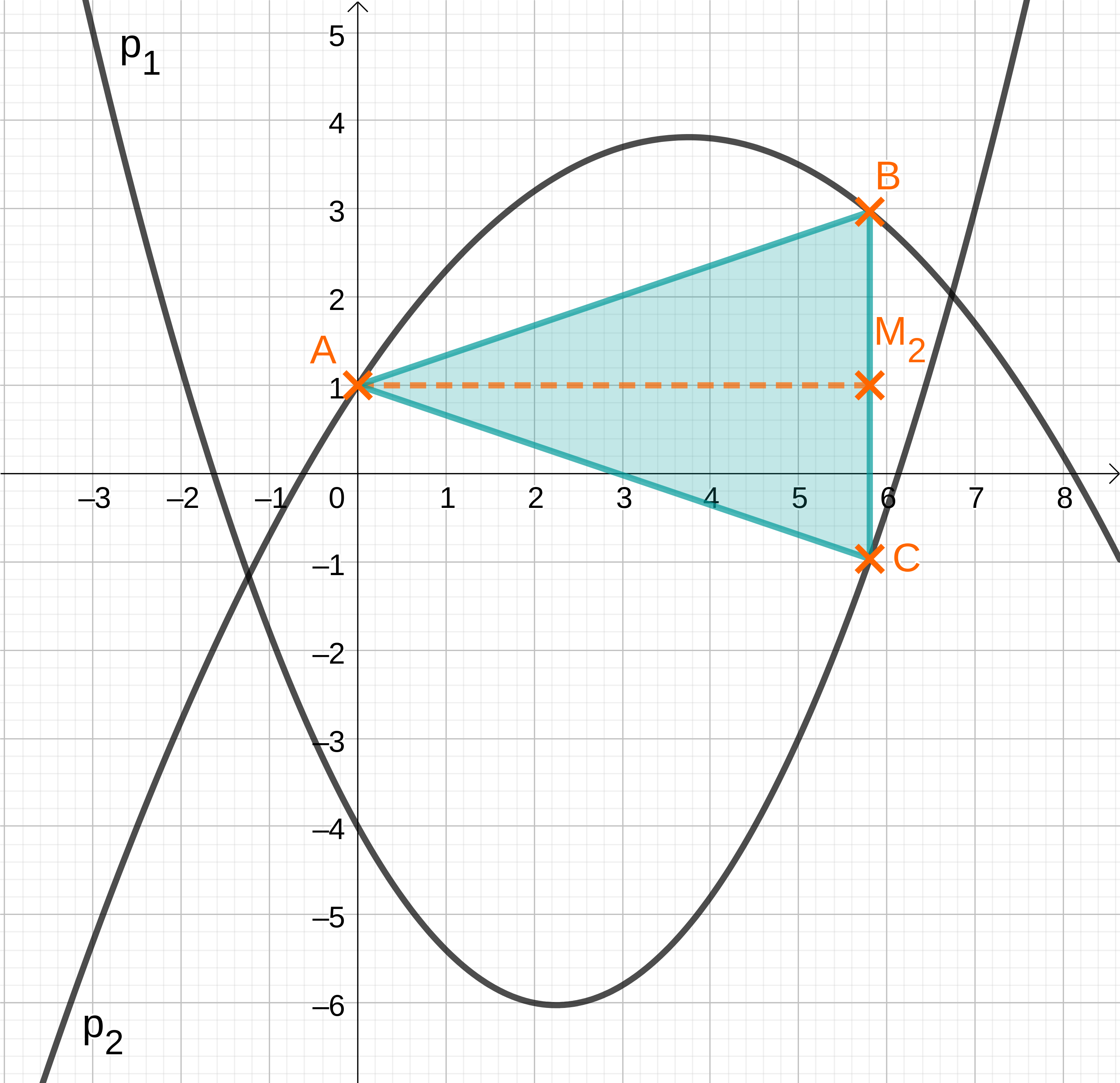
Die Mittelpunkte der Seiten haben dieselbe Abszisse wie die Punkte . Zeigen Sie, dass für die -Koordinate der Punkte gilt:
Das Dreieck ist gleichschenklig mit der Basis .
Berechnen Sie die -Koordinate des Punktes .
- 3
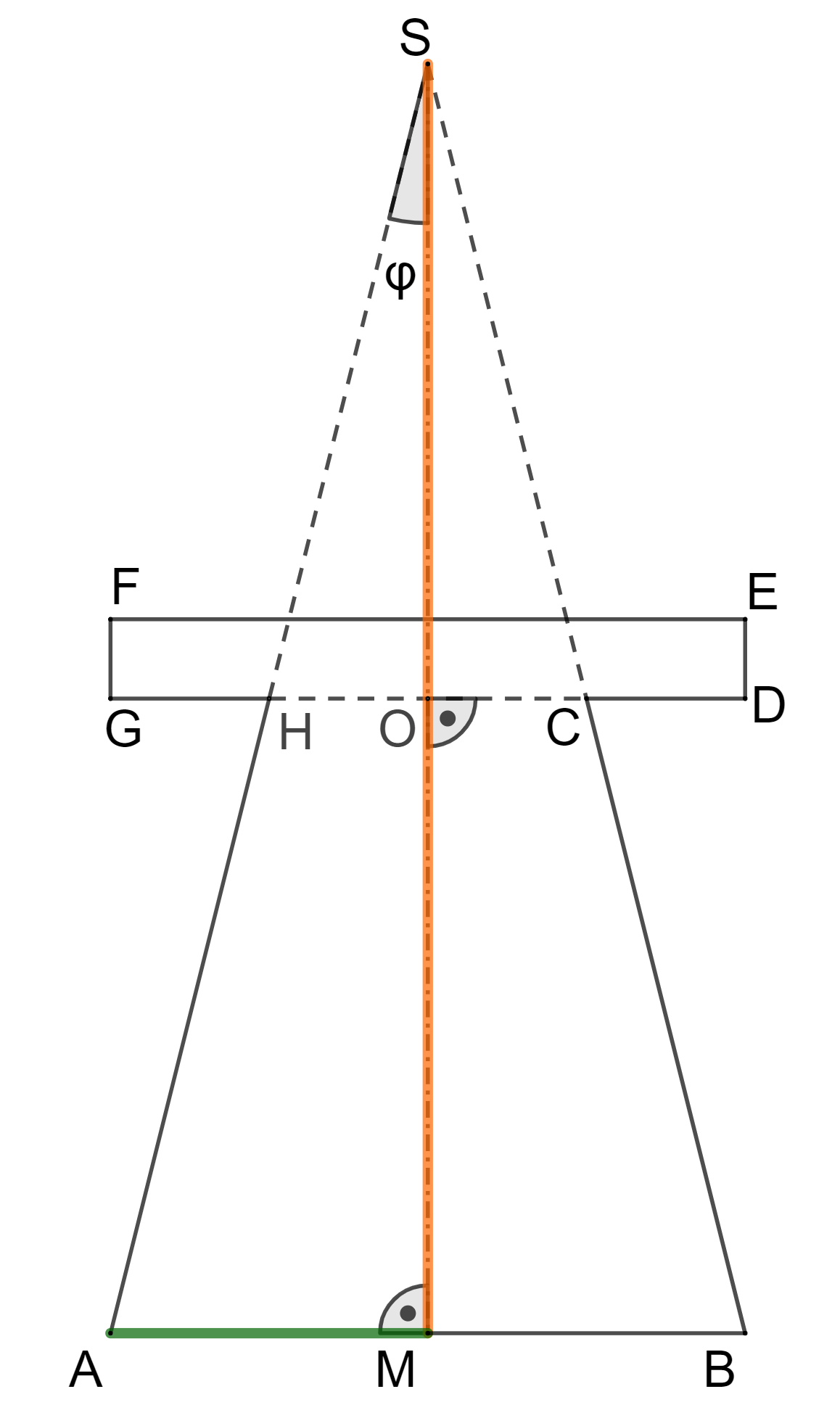
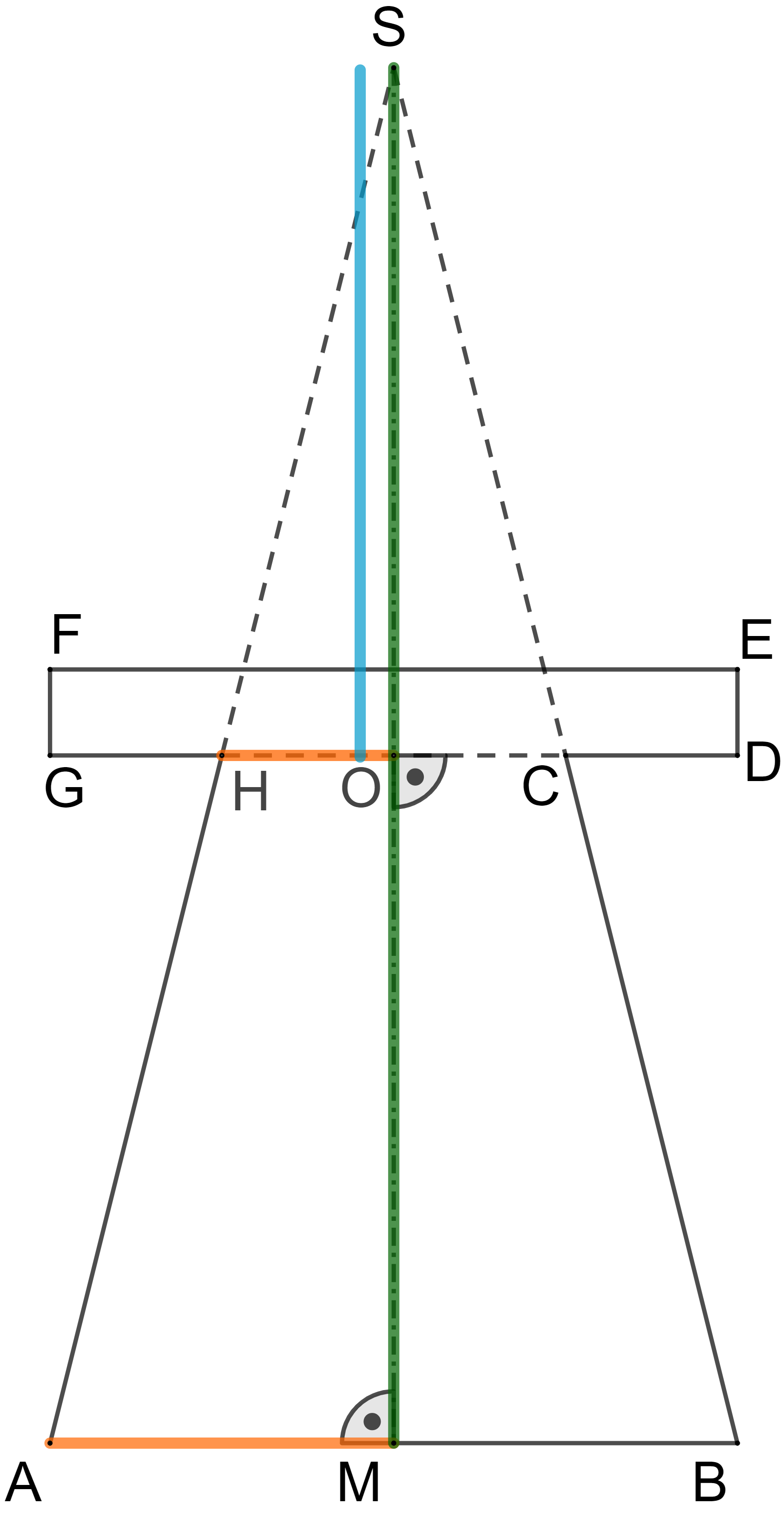
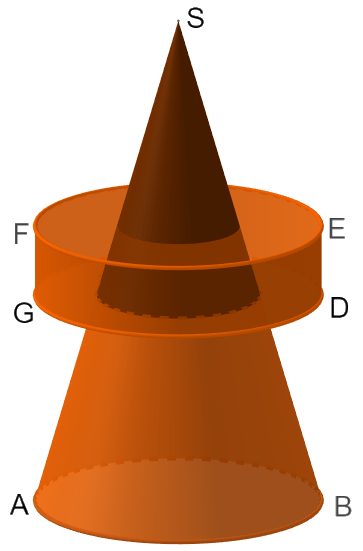
Die Skizze unten zeigt den Axialschnitt eines Körpers mit der Rotationsachse . Diese Skizze dient als Vorlage zur Herstellung einer Sitzgelegenheit. Es gilt:
Runden Sie im Folgenden auf eine Stelle nach dem Komma.
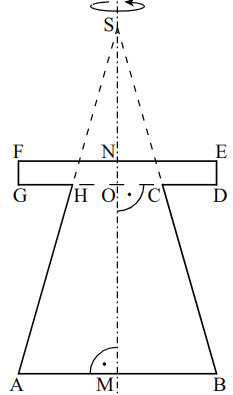
Berechnen Sie die Längen der Strecken und .
Ergebnisse:
Bestimmen Sie rechnerisch das Volumen des Rotationskörpers.