Teil B, Gruppe 3

Berechne das Volumen des symmetrischen Körpers.

Punkte: 4

cm³

Für diese Aufgabe benötigst Du folgendes Grundwissen: Volumen

Zur Lösung dieser Aufgabe solltest du wissen, was Prismen und Quader sind und wie du ihr Volumen bestimmst.

Die abgebildete Figur ist achsensymmetrisch und setzt sich in jeder Symmetriehälfte aus einem lila Körper, einem Prisma, mit der Grundfläche eines rechtwinkligen Dreiecks und einem roten Körper, einem Quader, zusammen.

Das Volumen eines lila Prismas kannst du mit der Formel $V_{P r i s m a} = G \cdot h_{P r i s m a}$ berechnen. Bevor du das Volumen des Prismas bestimmst, rechnest du zuerst die Grundfläche $G$ aus.

Flächeninhalt des rechtwinkligen Dreiecks

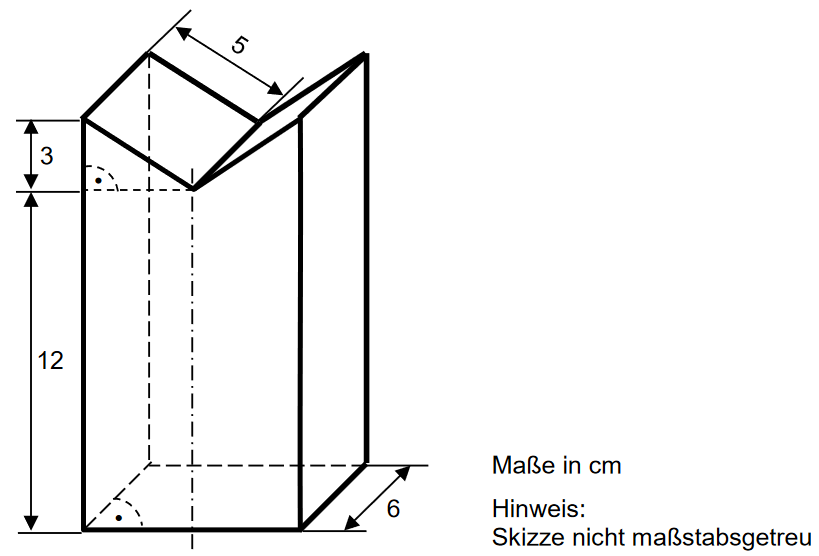
Die Grundfläche $G$ ist das rechtwinklige Dreieck. Den Flächeninhalt berechnest du mit der Formel $A_{△} = \frac{1}{2} \cdot g \cdot h_{△}$ , wobei die Höhe $h_{△} = 3 c m$ ist (siehe Skizze). Die Grundlinie $g$ berechnen wir mit dem Satz des Pythagoras, da wir ein rechtwinkliges Dreieck vorliegen haben.

$a^{2} + b^{2} = c^{2}$

Hier sind $a$ und $b$ die Katheten und $c$ die Hypotenuse.

Setze $a = h_{△} = 3 c m$ und $c = 5 c m$ ein und $b = g$ .

$h_{△}^{2} + g^{2}$	$=$	$c^{2}$
	↓	Setze die Werte ein.
$(3 c m)^{2} + g^{2}$	$=$	$(5 c m)^{2}$
	↓	Nun löst du die Potenzen auf.
$9 c m^{2} + g^{2}$	$=$	$25 c m^{2}$
	↓	Subtrahiere nun auf beiden Seiten der Gleichung $9 c m^{2}$ .
$g^{2}$	$=$	$16 c m^{2}$
	↓	Im letzten Schritt ziehst du noch die Wurzel.
$g$	$=$	$4 c m$

Die Grundlinie $g$ des rechtwinkligen Dreiecks entspricht $4 c m$ .

Im Folgenden setzt du die Grundlinie $g = 4 c m$ und die Höhe $h_{△} = 3 c m$ in die Flächeninhaltsformel für Dreiecke $A_{△} = \frac{1}{2} \cdot g \cdot h_{△}$ ein.

$A_{△}$	$=$	$\frac{1}{2} \cdot g \cdot h_{△}$
	↓	Setze $g$ und $h_{△}$ ein.
	$=$	$\frac{1}{2} \cdot 4 c m \cdot 3 c m$
	$=$	$6 c m^{2}$

Somit hat das rechtwinklige Dreieck eine Fläche von $6 c m^{2}$ .

Volumenberechnung eines Prismas

Nun berechnest du das Volumen des Prismas mit der vorher bestimmten Grundfläche des rechtwinkligen Dreiecks.

$V_{P r i s m a}$	$=$	$G \cdot h_{P r i s m a}$
	↓	Im ersten Schritt setzt du $G$ und $h_{P r i s m a}$ ein.
	$=$	$6 c m^{2} \cdot 6 c m$
	↓	Rechne das Volumen des Prismas aus.
	$=$	$36 c m^{3}$

Das Volumen des Prismas beträgt $36 c m^{2}$

Volumenberechnung eines Quaders

Nun wird noch das Volumen des Quaders bestimmt.

$V_{Q u a d e r}$	$=$	$l \cdot b_{Q u a d e r} \cdot h_{Q u a d e r}$
	↓	Wobei die Länge $l$ der Grundlinie $g$ des rechtwinkligen Dreiecks entspricht, also $l = g = 4 c m$ .
	$=$	$g \cdot b_{Q u a d e r} \cdot h_{Q u a d e r}$
	$=$	$4 c m \cdot 6 c m \cdot 12 c m$
	$=$	$288 c m^{3}$

Im letzten Schritt berechnest du noch das Gesamtvolumen, indem du das Volumen des Prismas und des Quaders addierst und mit zwei multiplizierst, da der Körper aus zwei solchen Hälften besteht.

$V_{g e s a m t}$	$=$	$(V_{Q u a d e r} + V_{P r i s m a}) \cdot 2$
	$=$	$(288 c m^{3} + 36 c m^{3}) \cdot 2$
	$=$	$648 c m^{3}$

Somit lautet die Antwort: Das Gesamtvolumen des Körpers beträgt $648 c m^{3}$ .

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org