Teil B, Gruppe 3

In einer Fensterscheibe sind vier gleiche, farbige Glasscheiben eingesetzt. Sie haben jeweils die Form einer Raute (siehe Abbildung). Berechne die Gesamtfläche des farbigen Glases. (4 Punkte)

Hinweis: Skizze nicht Maßstabgetreu.

Maße in cm.

cm²

Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächeninhalt eines Dreiecks

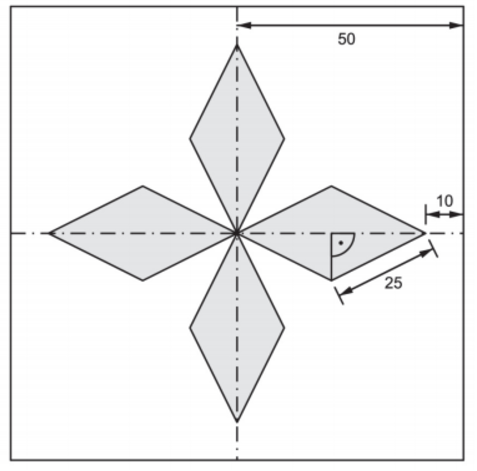
Um die Gesamtfläche des farbigen Glases zu berechnen, kannst du sie zuerst in vier gleiche Rauten aufteilen. Den Flächeninhalt dieser Rauten kannst du wiederum als vier kongruente, rechtwinklige Dreiecke berechnen, die entstehen, wenn du bei der Raute die Diagonalen einzeichnest.

Die kleinen kongruenten, rechtwinkligen Dreiecke werden während dem Rechnen als Dreieck $Δ$ bezeichnet.

Berechnung der längeren Kathete von Dreieck $Δ$

Um den Flächeninhalt von Dreiecken $Δ$ zu berechnen, werden die Längen von beiden Katheten des Dreiecks benötigt, da diese als Höhe und Breite des Dreiecks verwendet werden können.

Die längere Kathete kannst du berechnen, indem du zuerst die 10 cm lange Strecke von der 50 cm langen Hälfte der Seite des gesamten, quadratischen Spiegels subtrahierst. Dadurch erhältst du die längere Diagonale der Raute.

$50 cm - 10 cm = 40 cm$

Du teilst nun die längere Diagonale der Raute durch zwei, um die längere Kathete von Dreieck $Δ$ zu erhalten

$40 cm : 2 = 20 cm$

Berechnung der kürzeren Kathete von Dreieck $Δ$

Du kannst nun den Satz des Pythagoras anwenden, um die zweite, kürzere Kathete von Dreieck $Δ$ zu berechnen. Du kennst die Länge der ersten Kathete (20 cm) und der Hypotenuse (25cm), da die Hypotenuse gleichzeitig auch die Seite von einer der Rauten ist, von der die Länge schon in der Skizze angegeben ist.

$x^{²} {cm}^{2} + 20^{2} {cm}^{2} = 25^{2} {cm}^{2}$

Von beiden Seiten der Gleichung subtrahierst du $20^{2} {cm}^{2}$ .

$x^{²} {cm}^{2} = 25^{2} {cm}^{2} - 20^{2} {cm}^{2}$

Ziehe die Wurzel nun auf beiden Seiten der Gleichung.

$x cm = \sqrt{25^{2} {cm}^{2} - 20^{2} {cm}^{2}}$

$x cm = \sqrt{625 {cm}^{2} - 400 {cm}^{2}}$

$x cm = \sqrt{225 {cm}^{2}}$

$x cm = 15 cm$

Da nun beide Kathetenlängen, bzw. die Höhe und die Breite bekannt sind, kannst du nun den Flächeninhalt von Dreieck $Δ$ bestimmen.

$A_{Δ} = \frac{1}{2} \cdot 20 cm \cdot 15 cm = 150 {cm}^{2}$

Du erhältst die Gesamtfläche des farbigen Glases, wenn du den gerade eben bestimmten Flächeninhalt von Dreieck $Δ$ mit 16 multiplizierst, da die Gesamtfläche aus vier kongruenten Rauten besteht, welche sich wiederum jeweils aus vier kongruenten Dreiecken zusammensetzen.

$A_{gesamt} = 4 \cdot 4 \cdot A_{Δ} = 16 \cdot A_{Δ}$

$= 16 \cdot 150 {cm}^{2}$

$= 2400 {cm}^{2}$

Die Gesamtfläche des farbigen Glases $A_{gesamt}$ ist $2400 {cm}^{2}$ groß.

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das? serlo.org

Teil B, Gruppe 3

Berechnung der längeren Kathete von Dreieck Δ

Berechnung der kürzeren Kathete von Dreieck Δ

Berechnung der längeren Kathete von Dreieck $Δ$

Berechnung der kürzeren Kathete von Dreieck $Δ$